图像中非连续直线的提取方法

杨艳，汤自新

（四川大学计算机学院，成都610065）

0 引言

直线提取是图像处理中的一项重要内容，在道路提取和医学图像分析等方面都有着广泛的应用[1-6]。对于图像中存在的连续线条模式，如建筑物的轮廓、道路等中的直线信息提取已经有很多成熟的研究，常用的提取方法有基于LSD的直线提取算法[7]、基于相位一致性法[8]、启发式搜索法[9]、基于标记的直线提取[10]、基于惯性矩的直线提取[11]和Hough变换[12]等，这些算法通常是首先使用合适的边缘检测算法检测图像边缘，然后通过边缘点之间存在的联系形成直线。在提取图像中的非连续直线时，非连续直线可以看作由离散连通域组合而成，在这些算法的计算下，这些离散连通域被判定为方向各异的短直线连通域，或被连通为与目标直线模式不同的连通域，因此，传统的直线提取方法对于图像中的非连续直线提取并不适用。而许多物质的剖面结构，如金属、地震后的地块等，存在大量非连续直线，其目标点离散但具有直线特征，这些信息的提取可以用于金属内部的缺陷检测，灾害影响判断等方面，因此非连续直线提取方法的研究是至关重要的。

针对上述问题，本文提出了针对非连续直线的提取算法。首先，对图像进行二值化及滤波处理；其次，先利用图像膨胀连接离散连通域，再使用Steger算法[13]对滤波后的连通域进行中心线提取，得到可用于直线提取的线模式连通域；接着，采用切割算法对曲线连通域进行切分，确保每个连通域中只存在一条曲线模式，去除相交曲线对拟合结果的影响；最后，利用RANSAC（Random Sample Consensus）算法[14]结合最小二乘法对曲线连通域进行拟合得到直线方程，实现图像中非连续直线的提取。实验表明，本文提出的方法可以有效提取出图像中由离散区域组合的直线模式信息，实现图像中非连续直线提取。

1 相关算法

1.1 基于形态学和二值化的中心线提取算法

Steger算法[13]基于Hessian矩阵，能够实现图像中线形区域，如道路、血管等目标的中心线提取。然而对于图像中的离散区域组合成的线模式的中心线的提取，直接使用Steger算法存在以下问题：离散区域的形状大小各不相同，直接进行中心线提取必然导致所提取的线条碎片化，难以形成完整连续的曲线。

本文提出基于形态学的Steger算法，在进行线提取前，首先对图像进行二值化和形态学处理，使得不同的离散区域组成连续的连通域；此外，为了减少中心线提取的计算量，以及避免线条的误提取，算法进一步利用图像中连通域的面积特征对面积较大、不符合线条模式的区域进行了滤除，保证了算法的鲁棒性；最后，利用提取算法得到准确的中心线提取结果，获得非连续直线提取的预备点集。实现步骤如下：

（1）对待提取图像A进行膨胀处理。用一个8×8的矩形结构元素B遍历A中的每个像素并判断其是否为膨胀点，根据判断结果对图像进行膨胀处理，判断方式如下：

（2）确定每个连通域的大小及所包含像素点并进行滤波处理。操作流程如下：

①依次扫描图中像素点，将第一个没标记过的目标点存入向量；

②取出向量元素并扫描该点的8个邻接点，若是目标点，且没标记过，标记该点并存入向量；

③访问完向量中所有元素后按序寻找图像中下一个未被标记的目标点并存入新向量；

④循环b,c操作直到扫描完所有像素点。每一个向量即一个连通域，循环结束后形成不同连通域集合：

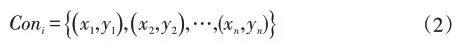
⑤分别设置高、低阈值thh、thl，去除阈值范围外的连通域得到滤波图像。

（3）提取目标图像中心线。对于曲线f(x,y)上的任意一点(x0,y0)，Hessian矩阵可以表示为：

其中dxx,dxy,dyy表示f(x,y)在(x0,y0)处的二阶导数。

图1 中心线提取示意图

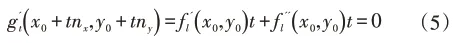
解得：

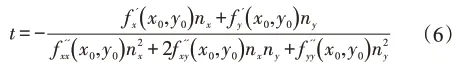
通过上式可以得到l上的极值点该极值点就是曲线的中心亚像素位置，若即中心 亚 像素位 置与在同一像素内，即可判定为曲线的中心点，依次判断图像中的目标像素点是否为中心点，即可得到用于直线提取的线模式连通域。

1.2 RANSAC最小二乘法

RANSAC算法[14]利用迭代的方式由观测数据估计出数学模型，具有很强的鲁棒性，在计算机视觉中应用广泛，能在含有错误数据50%的样本集中仍具很高的准确率。其基本思想是选择少而有效的初始数据集，然后在一定的容差范围内尽可能扩大数据集。利用RANSAC算法结合最小二乘法可以得到准确的直线拟合结果，算法实现如下：

（1）随机选择两点确定直线方程，并将符合该方程的其他点计为内点；

（2）循环（1）过程，找到内点归属最多的直线方程并确定选取的两个点作为初始点，对应的内点作为初始数据集。循环结束依据为e<ε，其中ε为设置误差，e为计算误差：

式中θ为内点数占所有目标像素点数的比值，k为当前循环次数。

（3）将初始数据集通过最小二乘法得到新的直线方程，并由该方程确定新的内点，扩充初始数据集。

（4）扩充后的数据集重复（3）过程得到最终的直线方程及内点集合。

2 非连续直线提取方法

2.1 流程设计

图像非连续直线提取方法流程如图2所示，各模块功能如下。

（1）图像预处理：对图像进行二值化处理，降低图像数据复杂性，利用滤波器去除干扰信息；

（2）基于图像形态学的中心线提取：提取图像中曲线的中心线；

（3）拟合预备点处理：滤波去除无用信息，细化曲线宽度至单像素，切割交叉曲线；

（4）RANSAC最小二乘法拟合：拟合直线并绘制。

图2 图像非连续直线提取方法流程

2.2 图像预处理

图像预处理分为两个步骤：①对图像进行自适应性二值化[15]，降低图像数据复杂性；②利用滤波器去除多余信息，如单个的点及较小的目标图像。图像自适应二值化首先计算积分矩阵I，I(x,y)表示点(x,y)与原点(x0,y0)组成矩形的灰度值总和，积分矩阵计算如下：

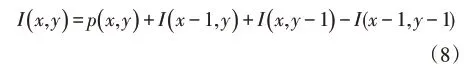
其中p(x,y)为像素点(x,y)的真实像素值。

图3 积分示意图

像素点(x,y)与其左上角像素点(x1,y1)构成一个矩形区域，如图3中矩形D，(x1,y1)是使得该矩形面积最大，且矩形边长不超过设定值的像素点。根据积分矩阵计算阈值thf矩阵公式如下：

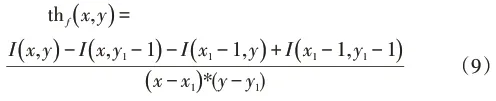
式（9）表示计算矩形区域D中的平均灰度值。当p(x,y)-thf(x,y)>thf(x,y)*t，像素点(x,y)为目标点，否则为背景点，其中t为阈值因子。根据上述阈值对图像像素点进行判断后得到二值图像，对二值图像进行连通域判断，并利用滤波器去除其中单个的点及较小的目标图像，可以有效减少图像中的多余信息。

2.3 基于形态学的中心线提取

中心线提取过程如下：首先，对二值化图像进行膨胀处理，连接其中的离散直线；接着，用滤波器去除其中连接而成的大面积区域以及细小无用信息；最后，使用Steger算法确定中心线点集，为后续步骤提供预备点。设二值图像为A，膨胀图像为C，设置矩形结构元素B为全1矩阵，图像A中像素点A(xi,yi)对应膨胀图像中的像素点C(xi,yi)，膨胀图像计算方式如下：

其中C(xi,yi)=1表示该点为目标点，否则为背景点；A(xi,yi)B表示将矩阵B的中心与A(xi,yi)重合进行卷积计算，遍历计算原始图像确定膨胀点后即可获得膨胀图像。以连通域面积为特征对膨胀图像进行滤波处理。

对滤波后的膨胀图像进行中心线提取，通过计算图像目标像素点对应的Hessian矩阵，求解最大特征值对应的特征向量，在特征向量方向进行泰勒展开计算确定中心点集合：

其中Coni表示不同连通域的中心点集，(xi,yj)表示i连通域中的所有中心点。

2.4 拟合预备点处理

2.4.1 Hilditch细化算法

经过中心线提取得到多个连接域Coni，其中仍存在孤立连通域，以及线连通域过宽的状况，因此在进行拟合前首先利用滤波去除其中较小的连通域，并对线连通域进行骨架提取形成单像素曲线，有效减少待处理数据。Hilditch算法[16]通过删除标记目标像素点完成线细化，像素标记过程如下：

（1）为每个目标像素点p建立八邻接域Conp8和四邻接域Conp4；

（2）遍历目标像素点，并根据Conp8连接数是否为1判断目标像素点是否为可删除点；

（3）删除所有标记点；

（4）重复（2-3）步骤直到没有新的标记点。

其中Conp8连接数计算公式如下：

这里Xi表示p的四邻接域像素，Xi+1,Xi+2表示p的八邻接域中Xi的后续点。通过标记可删除点并删除后得到细化后的图像。

2.4.2 线切割

若直接对细化后的线进行拟合，当存在两条或多条方向差异过大的相交曲线时拟合结果可能与真实结果完全不同，如图4所示，其中直线为拟合结果。所以本文提出一种线切割算法，在进行直线拟合前将相交的曲线切割为不同曲线，使相交曲线不能同时进行拟合，保证了最终拟合的准确性。切割方法如下：

（1）设置删除矩阵s为0，当像素点p为目标像素时，更新删除矩阵s：

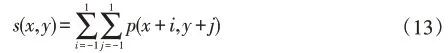
删除矩阵s表示p点8领域中目标像素点的数量。

（2）确定标记点，当s(x,y)≥4时，记录以p(x,y)为中心点的9×9范围图像中边界目标像素点的总数sum，其中相邻的目标像素点记为一个点，如图5中，sum=3；当sum≥3时，p(x,y)为曲线交叉点，将其标记为可删除点。

图4 直线拟合结果对比

图5 交叉点判断示意图

（3）通过删除图像中的所有标记点去除图像中相交曲线的交点，得到各不相交的曲线点集。

本文假设相交曲线中的最长线为目标线，其余分支为干扰信息，故在交叉点删除后的各曲线中选择最长线来进行拟合得到最终结果。

2.5 RANSAC最小二乘法拟合

提取到的中心线经过细化，切割及最长线选择后得到最终进行拟合的连通域，对该连通域中的点集拟合过程如下：

（1）在连接域Con中循环选择包含内点最多的初始点(x1,y1),(x2,y2)，并根据两点式判定初始直线方程y=f0(x)。

拟合直线方程为：

（3）根据直线方程y=f1(x)扩充内点集合并再次通过最小二乘法拟合得到最后结果y=f(x)。

（4）最后根据拟合模型y=f(x)以及初始点(x1,y1)，(x2,y2)，在原始图像中绘制得到提取直线。

3 实验结果与分析

3.1 实验数据与参数设置

本实验分别测试了不同类型离散直线的图像，如图6所示，图中都具有明显直线结构的离散点，由局部放大图可以看到，图中像素灰度值分布混乱，每个离散的区域形状各不相同，目标像素与周边像素差异非常不明显，与相应的其他可成线点间的联系也很微小，导致直接利用传统的直线提取方法对这些离散点进行提取非常困难。图6（a）的线条结构主要呈现竖直方向，其上半部分图像有分布均匀且不同于直线区域的大量像素点，这部分像素点在提取过程中必须去除，否则会影响直线提取的准确性；图6（b）具有倾斜直线特征，且直线特征较图6（a）更明显，通过放大图可清晰看到成线趋势；图6（c）同样呈现竖直直线特征，但像素间的差异性较图6（a）更小。

图6 测试图像及局部放大

实验中相关参数设置如下：实验中共进行了四次滤波处理，皆以面积作为特征值，四次阈值的设置分别为σ1=20，σ2=300，σ3=2000，σ4=200；图像膨胀选择的结构元素B为8×8矩形元素；自适应性二值化积分区域宽度设置值为150。

3.2 实验结果与分析

实验按照本文提出的提取步骤进行非连续直线提取，对中间关键提取步骤进行局部放大，如图7所示，其中从左到右分别为原始图像、二值化图像、膨胀图像、中心线提取、图像切割及最长线选择、提取结果。本实验在拟合过程中只选择了其中一个连接域作为拟合数据，所以提取结果只显示一条直线，图7中前两组图画线部分与目标像素点基本重合，表示图像中的非连续直线得到准确提取，而图7第三组图中的直线存在角度偏差，只在直线上半部分有所重合，这是因为直线下半部分在图像膨胀时被并入其他连接域，在后续一步滤波中被当作大面积连接域去除了，所以图7第三组图最后的拟合是通过上半截直线点集进行拟合，导致了最后结果与真实结果存在偏差。

提取中间过程对结果有着关键影响，因此本文对其中的关键步骤结果展开了讨论，以图7中第一组图像提取各步骤为例分析如图8。

图7 图像非连续直线提取的各步骤结果

图像二值化结果如图8（b）所示，从中可以看到自适应性二值化方法可以有效地将图像中的目标像素点从复杂背景中提取出来，像素灰度值只有0和1两种情况，大大减少了后续图像处理的计算量以及计算复杂度，二值化后的图像能够清晰分辨出具有成线潜力的离散点，能有效用于后续处理。

二值化图像中存在孤立目标点及很小的区域，在进行图像膨胀前经过滤波处理可以去除这部分无用信息，滤波结果如图9（a）所示。图像进行二值化及滤波处理后根据膨胀算法确定膨胀图像目标点即可获得膨胀图像，如图9（b）所示，对比二值化图像可以看到，经过图像膨胀后，离散的点与周围一定范围内的点相互连接形成不同的连通域，图像中已经出现明显的线条信息，但其中也存在大面积区域和孤立未被连接的点，这部分信息不能作为直线提取，甚至会影响提取效果，需要再次利用滤波处理去除这部分信息。

图8 二值化对比

图9 图像膨胀结果

图10 是中心线提取结果，图中可以看到根据膨胀结果进行中心点确认，可以准确地确定图中曲线位置。结果显示，本文提出的基于图像形态学处理的Steger算法能有效地对非连续直线进行定位得到预备点集。

图10 中心线提取结果

对中心线提取结果进行简单的线细化及切割处理，可以去除其中的大量多余信息，图像切割结果如图11所示，图中曲线的交点被标记为可删除点后删除，得到不相交曲线，形成不同连接域，确保待拟合连接域中不存在相交曲线，能有效提高拟合正确性得到提取结果。

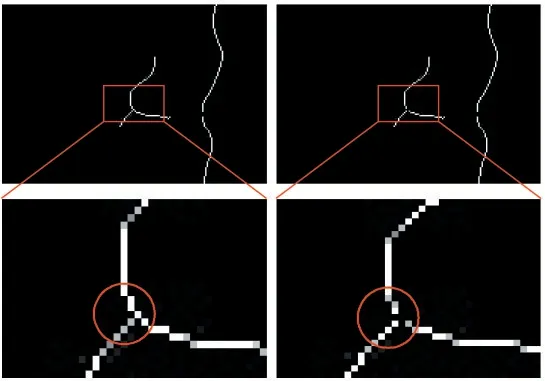
图11 图像切割结果

拟合预备点经过RANSAC最小二乘法拟合结果如图12所示，其中左边为待拟合点，右边为绘制在原始图像上的拟合直线，可以看到拟合直线与原始图像中的目标像素点基本重合，表明本实验成功提取出图像中的非连续直线。

图12 直线拟合结果

根据提取结果分析，本文提出的基于图像形态学处理的Steger算法能有效地对非连续直线进行定位得到预备点集，同时对预备点进行细化切割处理也大大提高了后续拟合算法的正确性，最后本文选用RANSAC最小二乘法进行对预备点集进行准确拟合，增强了算法的稳定性。本文在提取过程中多次进行了滤波处理，不断对多余信息及干扰信息进行筛选去除，是提高直线提取准确性的有效方法。

4 结语

针对非连续直线难以被提取的问题，本文提出通过自适应性算法进行图像二值化，降低图像灰度信息复杂度，然后提出利用基于图像膨胀的形态学方法的Steger中心线提取算法对曲线进行中心线提取得到粗略的线段信息，最后利用RANSAC最小二乘法进行直线拟合得到精确的直线提取结果的提取方法，在整个提取过程中还多次以面积作为特征对图像目标信息进行滤波处理，有效减少了其中的干扰及多余信息，并且本文还提出在进行拟合前用切割算法对拟合数据进行切割处理，以去除交叉曲线对拟合结果的影响。实验结果表明，本文提出的非连续直线提取方法可以有效地提取出图像中的非连续直线，对于图像中的非连续直线间距稍远的直线提取效果更佳，对于图像中直线分布较密的情况，图像膨胀算法会导致一些相邻直线被连通到同一个连接域，影响最后提取结果，因此在应用于直线分布较密的图像时还需进一步改进。