如何利用数学基本活动经验来培养核心素养

本文以“长方形、正方形面积的计算”一课为例，通过操作、探究、复合、思考等数学基本活动经验初步尝试培养学生的核心素养。具體内容如下：

一.直观想象与数学运算：

老师：现在有一个长为6厘米，宽为3厘米的长方形，用什么办法能求出这个长方形的面积呢？

学生：可以用面积为1平方厘米的正方形做单位摆一摆，看这个长方形里有几个1平方厘米。

老师：很好，那就请大家现在开始分组摆一摆吧。

学生分组操作后得出以下结论：

学生1：我刚好摆了18个面积为1平方厘米的正方形，所以这个长方形的面积是18平方厘米。（如图一）

学生2：我每行摆了6个，可以摆3行，所以它的面积是6×3=18平方厘米。（如图二）

分析：本节课中学生围绕“如何求出已知长方形的面积”这一问题展开了一系列行为操作和计算活动，学生在自己动手摆一摆后发现了两种得出长方形面积的方法，其中第二种方法还对数据进行了运算，这也就运用到了操作的经验和探究的经验，从而使学生的直观想象和数学运算两大核心素养得到了一定的培养。

二.数据分析和逻辑推理

老师：刚刚两个小朋友用了两种不同的摆法，但是他们得出来的结果都是18平方厘米，那么大家想过吗，第二个小朋友，她用的6乘3得到的长方形的面积，那么大家想想是不是所有的长方形的面积都可以用这个方法来计算呢？下面我们就来做一个试验，请大家进行小组活动：任选若干个面积为1平方厘米的小正方形来拼成不同的长方形，观察一下，长方形的面积与它的长和它的宽有什么联系呢？

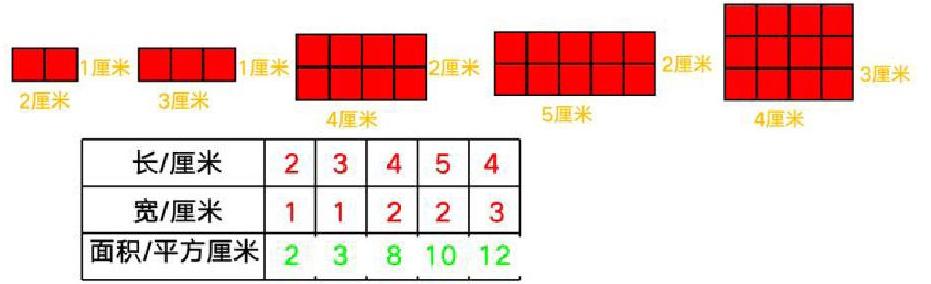
老师：好，让我们一起来看一看第一组的同学们的摆法和他们所得到的数据。

老师：我们一起看第一个长方形，它的长是2厘米，宽是1厘米，它的面积是2平方厘米;第二个长方形，它的长是3厘米，宽是1厘米，它的面积刚好是3平方厘米;再看第三个，它的长变成了4厘米，宽变成了2厘米，按照刚刚的计算方法得出来它的面积应该是4×2=8平方厘米吧，那么大家来数一数它里面的小正方形是不是8个呢？

学生：是8个！

老师：那么用小正方形得出来这个长方形的面积也刚好是8平方厘米吧！接下来请大家再看看后面两个长方形的面积是不是也适用这个计算方法呢？

学生：长是5厘米，宽是2厘米的长方形，算出来面积是5×2=10平方厘米，再数一数刚好是10个小正方形。

老师：没错，如果我们继续做下去，你会从这一组组的数据中发现什么呢？能得到长方形面积的计算方法吗？

学生：长方形的面积就等于它的长乘以它的宽！

分析：以上片段便采取“数形结合”的方法将长方形的长、宽、面积通过列表的方式与操作图形一一对应，为了让学生能有第一手的直观感受，老师组织学生以小组的形式自己摆一摆进行实际操作，学生在得到数据后带着“长方形的面积与它的长和它的宽有什么联系？”这个疑问进行数据分析与证明归纳，这一整个过程就运用到了上文中提到的操作的经验、探究的经验和思考的经验，即复合的经验，学生要自己从各组数据中探究规律并推理分析之后得到长方形面积的计算公式，那么，学生的数据分析和逻辑推理的素养便得到了一定的培养。

三.数学抽象与数学建模

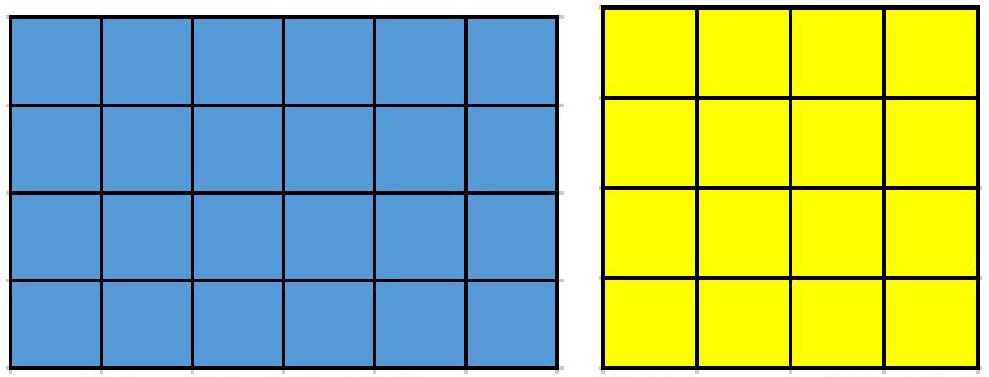
老师：刚刚大家已经得出了长方形的面积公式，那么，请大家计算下面两个图形的面积。

学生：长方形的面积是6×4=24平方厘米;正方形的面积是4×4=16平方厘米。

老师：哦？正方形的面积也可以用这个方法算吗？

学生：正方形可以看成是长和宽相等的长方形，所以也可以用长方形面积的求法算出来。

老师：大家真棒，因为正方形是特殊的长方形，我们是不是可以将正方形的面积公式归为：正方形的面积=边长×边长呢？不信的话，大家可以拿起你们的小正方形随意摆一摆来验算这个结论。

分析：上述片段在推理正方形面积的计算公式时，学生自己说到的“正方形就是长和宽相等的特殊的长方形”这一概念中为长方形的概念增添一个“长和宽相等”的限制条件后变成正方形的概念的过程就是一种强化结构式抽象过程，并且两个计算公式的确立涉及到了数学建模。学生通过类比长方形面积的计算公式而推导出正方形面积的计算公式这一过程就运用到了思考的经验，而在此过程中学生们数学抽象和数学建模的素养也得到了一定的培养。

综上所述，通过数学活动经验来培养数学核心素养是相当容易的，只是数学核心素养的培养是一个“长征”过程，不是一两节数学课更不是一朝一夕就能达到一个很高的水平的，这需要我们每位教师的不懈努力，通过各种数学活动经验的使用让学生真正成为课堂的主人，时刻牢记培养学生数学核心素养这一任务，将两者良好结合，创造出更多受学生喜爱又高效的课堂。

上述课程的开展过程不一定准确，欢迎各位老师批评指正。

作者简介：张紫薇（1997.10-），女，汉族。湖南湘潭，硕士研究生。湖南科技大学，学科教学（数学）