向量法在求解几何问题中的应用

摘 要：向量是建立代数、函数、几何问题之间联系的纽带，作为一种解题方法在简化相应问题、提升解题效率上非常实用，文章主要探讨向量法在几何命题、三角函数、不等式以及动点轨迹四个方面的应用，最后给出了在解析几何教学中的几点建议。

关键词：向量法;代数化;动点轨迹;Matlab软件

中图分类号：O182 文献标识码：A

解析几何是数学专业的基础课，可以说是其他数学课程的基础，是高等数学类课程的基石。线性代数，数学分析，常微分方程等课程的学习都离不开解析几何的基本知识及研究方法。其基本思想是用代数的方法来研究几何，数学家笛卡儿曾说过：一切问题最终都可以转化为数学问题，一切问题可转化为代数问题进行研究，虽然这种说法过于绝对，但是很好地说明了用代数中的方法去研究几何问题的重要性。为了把代数里涉及的运算引进到几何中，最根本的做法就是设法把空间的几何结构有系统的代数化、数量化。

几何中最基本的单位是“点”，点成线、线成面、面成体，而代数中最基本的单位是“数”，要建立几何与代数之间的关系，就需要建立“点”与“数”之间的关系，即借助空间坐标系来实现[1]。

向量是一个既有大小又有方向的矢量，通过直角坐标系可以将向量的分量分别给出，因此在研究几何问题中起着重要的作用。本文主要介绍利用向量求解四类几何问题。

一、向量方法在几何命题证明中的应用

传统的几何命题都是利用已知条件之间的各种变换和构造辅助线来证明，这种方法往往复杂，如果找不到隐含的信息，则无从下手，但是利用向量法却事半功倍。

例1：利用向量法证明四面体对边中点的连线交于一点且互相平分。

二、向量法在三角函数中的应用（正弦、余弦定理）

正弦、余弦定理的证明方法有很多[2-3]，比如做辅助线和外接圆，在高中对于学生来说是非常困难的，证明过程复杂、懊悔难懂，一般情况下只有记忆公式没有理解，在大学的学习中讲解了向量的数量积和向量积之后，作为向量的应用外拓，利用向量法证明，学生理解得更透彻，进而对学习向量法产生兴趣。

三、向量法在不等式中的应用

柯西——施瓦兹不等式有着非常广泛的应用，如求函数极值、求解方程、求解三角与几何问题等方面，证明方法有直接法和三角函数变换证明[4]，构造二次函数法、归纳法、配方法[5]等，向量法证明相对于上述方法更简单易懂。

四、向量方法在动点轨迹中的应用

例4：把一根线绕在一个固定的圆周上，将线头拉紧后向反方向旋转，以把线从圆周上解放出来，使得放出来的部分成为圆的切线，求线头的轨迹方程。

分析：若将线头的轨迹方程以普通方程的形式表示，显然是非常困难且不容易求解的，并且轨迹方程不唯一，但是如果利用向量法来求解动点的轨迹方程，是比较简单的，只需要理解线头动之前和动之后的向量关系，那么求解过程简单直接，降低了问题的难度。

这种曲线叫做圆的渐伸线或者切展线，在工业上常被称作齒轮曲线[6]。利用向量的方法求解类似的问题，如内旋轮线、外旋轮线等问题的动点轨迹亦是非常简便的。

在解析几何教学中笔者有以下三点建议：

一是解析几何是一门比较抽象的课程，课前应给学生提供相应的学习材料，如慕课资源，课中讲解应启发式的指导学生学习，使学生将高中知识与大学知识衔接起来，而不是脱节;

二是解析几何中有很多的运算，包括向量的运算和直线、平面的方程求解、直线与平面之间的关系等，在学习的过程中应注重学生计算能力的培养，避免出现上课听着会考试不会的情况发生;

三是学生对于空间中的几何图形比较陌生，在上课的时候锻炼学生数形结合的能力，比如在空间中，方程x2+y2=1代表圆柱，学生第一反应是圆，因此在平时的教学活动中应适当的利用Matlab软件演示一些几何图形，这样学生容易理解、记忆深刻，而且在无形中向学生介绍了Matlab软件，这对学生后期的学习奠定了基础。比如心形线极坐标方程r=a（1-sinθ），a是常数。代码为：

clc;clear

%r=2（1-sin（theta））

theta=[0：0.01：2*pi];

polar（theta，2*（1-sin（theta）），'-k'）

polar（theta，2*（1-sin（theta）），'-ok'）

title（'极坐标系下的心形线'）

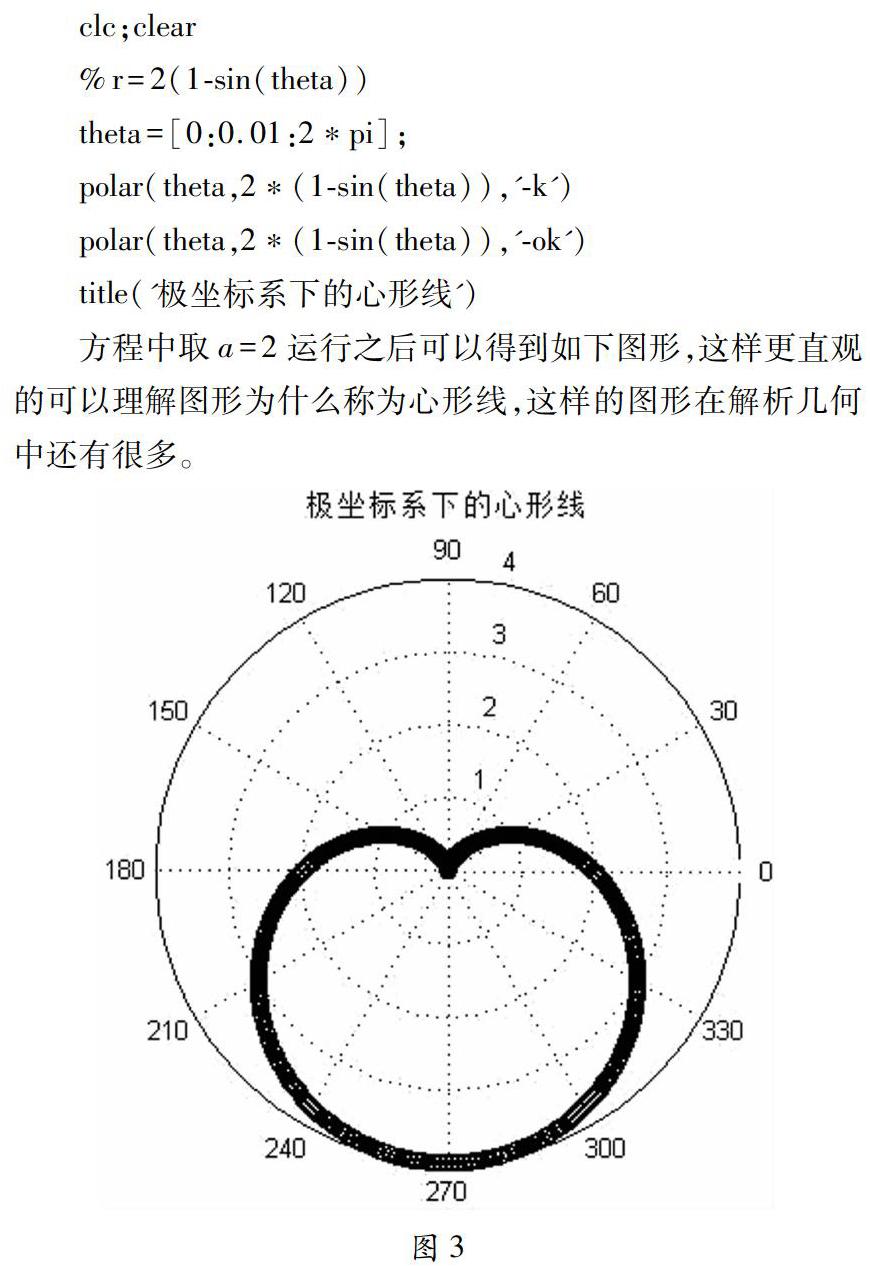
方程中取a=2运行之后可以得到如下图形，这样更直观的可以理解图形为什么称为心形线，这样的图形在解析几何中还有很多。

五、结语

以上是向量法在四类问题中的应用以及在教学中的三点建议，当然向量法还有很多应用，比如求解直线方程，求解平面方程，求解定比分点问题等等，在此不一一列举。向量法为求解上述问题提供了一种新途径，使得解题思路简单，化难为易，事半功倍。

参考文献：

[1]滕吉红，等.浅析高等数学中蕴含的思维观和方法论[J].高等数学研究，2020，23（4）：124-127.

[2]赵冬梅.正弦定理、余弦定理的证明方法探究[J].西北成人教育学报，2012，6，137-140.

[3]宋现印.深入应用领域，探讨向量解法[J].数学教学通讯，2019，10，78-79.

[4]龚加安.柯西不等式的证明及几何解释[J].读与写杂志，2018，15（12）：34-35.

[5]黄韬，顾华强.柯西不等式的证明与应用.数学学习与研究，2018（3）：108-109.

[6]吕林根，许子道.解析几何（第四版）[M].北京：高等教育出版社，2006.

作者简介：苏晓璐（1989— ），女，回族，宁夏人，硕士，助教，研究方向：偏微分方程数值解法。