基于OSGEarth值域填充问题的一种解决方法

邹韬 李雪 杨东升 华彩成

摘要：利用OSGEarth技术，基于算法模型计算数据，利用delaunay三角网逐点插入法，解决任意区域值域填充技术难题，对于科学计算数据可视化分布显示具有普适性。程序以插件的形式进行封装，具有较高的工程应用价值。

关键词：OSGEarth;Delaunay三角网;科学计算可视化;插件

中图分类号：TP311       文献标识码：A

文章编号：1009-3044（2020）34-0020-03

Abstract：This paper uses OSGEarth technology to calculate data based on algorithm model， and uses Delaunay triangulation point by point insertion method to solve the technical problem of filling arbitrary range. It has universality for the visualization of scientific calculation data distribution. The program is encapsulated in the form of plug-in， which has high engineering application value.

Keywords： OSGEarth;Delaunay triangulation;visualization of scientific computing;plug-in

1概述

所谓“OSGEarth值域填充问题”是指以OSGEarth平台为基础，已知任意物理量在空间的离散分布，依据颜色列表与物理值对应关系，填充该物理量任意分布区域的问题。是科学计算可视化重要课题之一，无可回避。

1.1 OSGEarth简介

OSG是OpenSceneGraph的英文缩写，它是一个开放的图形场景库，主要为图形图像应用程序的开发提供场景管理和图形渲染优化功能。它包括OSG核心库、OSG工具库、OSG插件库，及在此基础上开发出来的OSG应用程序。OSGEarth是带有GIS功能的OSG图形库，它对OSG做进一步封装，加入对地理信息系统场景管理插件、地理数据解析插件和用户交互插件，功能更加强大，其主要特点如下：

（1）OSGEarth是一款开源的、基于OSG的地理信息系统框架库，具有良好的场景控制和地理信息管理能力。

（2）OSGEarth可加载多种地理信息数据源，数据源格式需符合数据驱动格式要求。数据类型包括：卫星影像数据，高程数据，矢量数据等。数据源多为金字塔式的瓦片数据，可极大提高系统数据加载和图像渲染速度。

（3）平台的场景管理方式是“场景节点树”结构，场景树顶端的节点（osg：：Geode）包含各种需要渲染的几何顶点和渲染状态信息;根节点（osg：：Group）及其派生出的各种特殊功能节点则作为场景树的各个枝节节点，它们也可以拥有不同的渲染状态机;有且只有一个节点可以直接作为整个场景的根节点，使用setSceneData将其设置给场景的视镜器系统，即等同于将整个场景树传递给渲染树和显示系统。

（4）图形渲染功能由渲染树完成。过程包括：用户选定场景，场景筛选以及绘制。场景树构建完成，平台利用渲染器，遍历视镜器中每个叶子节点，设置场景树各叶子节点状态机，实时完成更新场景树，根据用户选定场景，裁剪多余的叶子节点，保证渲染速度流畅、快速。

（5）用戶交互功能由事件处理器和场景漫游器完成。在系统每一帧的仿真过程中，事件处理器负责处理图形窗口设备传递到事件队列_eventQueue的各种事件，主要有键盘事件、鼠标事件。场景漫游器取得主摄像机的视口范围，计算主摄像机的VPW矩阵。完成场景坐标转换、放大、缩小和漫游等功能。

1.2 ITU-R.P533计算模型

该预测模型适用于最长为7000 km的路径的射线路径分析、超过9000 km时应用从拟合到测量数据的复合模式经验公式，在7000-9000 km距离范围内应用这两种方法之间的平滑过渡。

确定了给定增益的无损接收天线的月平均基本MUF、入射天波场强和可用接收机功率。该方法包括用于预测数字系统性能的信道传输函数的参数估计。给出了电路可靠性评估的方法。信号强度根据ITU R测量数据库进行标准化。该方法要求在指定的“控制点”确定若干电离层特性和传播参数。

在赤道地区，在晚上（当地时间），由于区域电离层结构不稳定性，预测结果有可能出现偏差，而这种不稳定性并没有被该方法完全考虑在内，需要完善。

1.3 Delaunay三角网

Delaunay三角网具有最大的最小角及空外接圆两大重要性质，使得剖分所得每个三角形最大限度地接近正三角形，因此它在所有的构网原则中是最优的，这使得它作为一种基本手段在计算流体力学，地质建模，科学计算可视化、地理信息系统、逆向工程等领域得到越来越多的应用。Delaunay三角网具备以下优异的特性：

（1）最接近：以近期临的三点形成三角形，且各线段（三角形的边）皆不相交。

（2）唯一性：无论从区域何处开始构建，终于都将得到一致的结果。

（3）最优性：随意两个相邻三角形形成的凸四边形的对角线假设能够互换的话。那么两个三角形六个内角中小的角度不会变大。

（4）最规则：假设将三角形网络中的每一个三角形的最小角进行升序排列，则Delaunay三角形网络的排列得到的数值最大。

（5）区域性：新增、删除、移动某一个顶点时仅仅会影响临近的三角形。

（6）具有凸多边形的外壳：三角网最外层的边界形成一个凸多边形的外壳。

2原理与实现

2.1原理

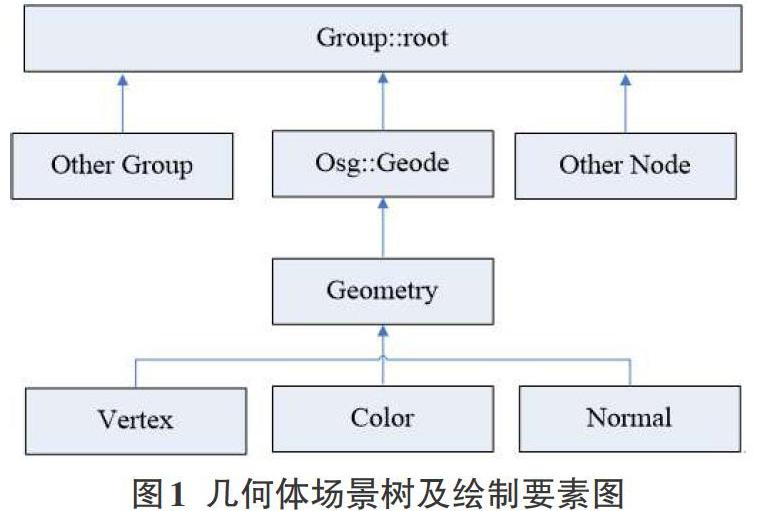
在OSGEarth场景中所有绘制的节点数据都会加入一个osg：：Group根节点中，而几何图元作为一种需要绘制的对象也有类似的数据结构，这个类就是osg：：Geode，它的作用就是组织绘制图元对象要素，图元状态机等参数，然后，加入osg：：Group中，在视镜器中渲染显示。图元对象要素包括顶点Vertex，颜色color，顶点关联方式和法线以及数据解析。结构如图所示：

从图中可以看出，首先要申请一个osg：：Geometry，然后设置图元对象要素。具体步骤如下：

（1）指定向量数据。包括设置图元边界向量数据、纹理坐标数据和顶点颜色值等一系列向量数据。可以通过下面几个函数来实现：

void setVertexArray（Array *array）;

void setVerterData（const ArrayData&arrayData）;

void setColorArray（Array *array）;

void setColorDara（const ArrayData&arrayData）;

（2）设置绑定方式。包括依据离散点值与颜色对应关系，设置颜色容器和纹理坐标的法线。可以通过下面函数实现：

Void setNormalBinding（AttributeBinding a）;

Void setColorBinding（AttriburreBinding a）;

（3）数据解析。指定图元各种向量数据和图元绑定方式之后，需对向量数据进行解析。这里采用delaunay三角网算法，将向量顶点数据以基础单元类型osg：：PrimitiveSet：：TRIANGLES，进行解析。具体解析过程详见后续章节。

（4）各圖元参数设置完成后，加入osg：：Geometry中渲染，使能叶子节点，加入场景树根节点，在视景器中图像更新显示，完成图元绘制。

2.2 实现

本程序采用C++语言编程，利用其语言本身简洁、使用灵活、数据结构系统化、控制流程结构化、可移植性好等优点，在编程过程中尽量发挥语言优势。程序以插件的形式进行封装，方便系统集成调用，工程应用价值较大。

利用ITU算法模型，指定发射机发射功率，天线发射增益，接收增益，工作频率等工作参数，设定通信成功信噪比，给出不同工作频率，指定目标区域的通信信道信噪比数据。在osgEarth系统平台上，应用该科学计算可视化插件，给出通信信噪比分布图，设定可通信噪比门限下限值，进而判断通信可通率情况，方便后续项目工作展开。程序工作流程图如下：

利用delaunay三角网算法，解析图元离散点可通信噪比数据子程序的结构流程图如下所示：

主要代码如下所示：

m_rpHGeo = new osg：：Geometry;

m_rpHGeo->setDataVariance（osg：：Object：：DYNAMIC）;

m_rpHGeo->setUseDisplayList（false）;

m_rpHGeo->setUseVertexBufferObjects（true）;

m_rpHGeo->getOrCreateStateSet（）->setRenderBinDetails（11，"DepthSortedBin"）;

osg：：ref_ptrpArrayXYZ = new osg：：Vec3Array;

osg：：ref_ptrpColorArray = new osg：：Vec4dArray;

osg：：ref_ptrrpDrawEle=newosg：：DrawElementsUShort（osg：：PrimitiveSet：：TRIANGLES）;

m_CdlauNay->push_backPt（pArrayXYZ）;

m_CdlauNay->createTn（）;

int triNum = m_CdlauNay->findTriNum（）;

long p0No=0，p1No=0，p2No=0;

for（int i=0;i

{

for（int j=0;j

{

m_CdlauNay->findPointIndex（j，p0No，p1No，p2No）;

if（i == p0No || i == p1No || i == p2No）

{

rpDrawEle->push_back（p0No）;

rpDrawEle->push_back（p1No）;

rpDrawEle->push_back（p2No）;

}

}

}

m_rpHGeo->setVertexArray（pArrayXYZ）;

m_rpHGeo->setColorArray（pColorArray，osg：：Array：：BIND_PER_VERTEX）;

m_rpHGeo->addPrimitiveSet（rpDrawEle）;

m_rpHGeode->addDrawable（m_rpHGeo）;

osg：：Group root->addchild（m_rpHGeode）;

不同工作频率可通信噪比分布图如下所示：

3结束语

本文以osgEarth地理信息平台为基础，提出利用Delaunay三角网算法，解决科学计算可视化值域填充问题的一种方法。该方法结构清晰、使用灵活，适用二维任意域离散点数值填充问题。程序以插件形式封装，方便系统集成、调用，具有较高的工程应用价值。本方法目前只适用二维值域填充问题，对于三维值域填充问题，需要做进一步研究和实现。

参考文献：

[1] 蒋瑜，杜斌，卢军，等.基于Delaunay三角网的等值线绘制算法[J].计算机应用研究，2010（1）：101-103.

[2] 方勇，刘鹏，胡海彦.一种Delaunay三角网的快速生成算法[J].测绘科学与工程，2006，26（3）：16-20.

[3] 武晓波，土世新，肖春生.Delaynay三角网的生成算法研究[J].测绘学报，1999，28（1）：28-35.

[4] 肖鹏，刘更代，徐明亮.OpenSceneGraph三维渲染引擎编程指南[M].北京：清华大学出版社，2010.

【通联编辑：梁书】