基于MEA优化Chaos-Elman模型的车载ATP故障率预测研究

刘奇，王俊峰

(北京交通大学 轨道交通控制与安全国家重点实验室，北京100044)

车载ATP 是保障列车运行安全的重要信号设备，如果ATP 出现故障且不能得到及时的维修将会大大影响铁路系统的运输效率。目前，铁路系统关于ATP 的日常运维存在2 个比较明显的问题，第一是ATP 的维修备件并不是依据科学合理的计划进行储备的，即备件的数量并不一定和实际需求相匹配，因而容易出现储量不足导致维修工作无法正常进行或者储量过多超过实际需求造成浪费的情况；第二是铁路信号设备众多且都需要占用有限的维修资源，因而容易出现资源分配不合理的情况，影响ATP 的维修工作。通过ATP 的历史故障率时间序列来预测其未来短期故障率变化趋势则可以有效地解决上述问题。如果预测故障率呈现增长的趋势，则需要相应地增加维修备件的储量以满足未来的需求同时应该分配更多的维修资源并加大检修力度；反之，则可以适当减少备件的储量避免浪费并把多出的维修资源分配给其他故障率较高的设备，做到人力物力的合理利用。为了对ATP 故障率实现高精度的预测，本文采用混沌理论，Elman 神经网络(ENN)以及思维进化算法(MEA)构建故障率组合预测模型。朱子虎等[1]把混沌理论用于铁路客货运量预测，在相空间重构的基础上借助最大Lyapunov 指数预测法利用历史数据实现了对未来6 a 内铁路客货运量的有效预测。Hasnaa 等[2]为了更精准地对光伏功率做出预测，把光伏功率时间序列相空间重构之后的结果建立数据库作为神经网络的输入，并和直接使用神经网络的预测结果对比，表明引入混沌理论能更好地分析数据的变化规律。李媛等[3]针对电力负荷数据的混沌性，把相空间重构和Elman 神经网络相结合进行工业用电预测，通过实测数据的仿真验证了Chaos-Elman 模型的效果优于单一模型。Elman 神经网络是一种动态反馈网络，相比BP 等前馈网络具有更强的映射能力。WANG 等[4]把经验模态分解(EMD)和ENN 结合，利用EMD 分解原始风速数据并用ENN 对每一个子序列建模，最终构造了一种新型的混合风速预测模型，通过对比证明了ENN 的拟合性能优于BPNN。艾格林等[5]把ENN 用于光伏发电功率预测，表明相对其他网络，ENN 的输入延迟特性更适用于预测建模。传统的ENN 往往存在易陷入局部最优等不足，针对这一点，采用MEA 算法优化ENN 的权值阈值。孙俊等[6]应用MEA 优化BP 神经网络用于大米水分含量高光谱检测并和遗传算法作对比，证明了MEA-BP 比GA-BP 具有更高的预测决定系数。崔江等[7]通过MEA 优化极限学习机的训练参数用于航空发电机旋转整流器的快速故障分类问题，相比GA 优化的结果具有更高的诊断正确率。目前，关于车载ATP 的故障率预测研究的相关文献相对较少。鉴于上述算法在其他领域取得了很好地预测效果，本文在小波去噪的基础上结合上述3 种算法提出了一种基于MEA-Chaos-Elman 的ATP 故障率预测模型，并通过实测数据的仿真实验验证了所提出的模型有效可靠，能够解决本文的预测问题。

1 原始数据小波去噪

本文的故障率序列根据2014-01-01～2017-12-31 全路网范围内某类型ATP 设备的故障数据利用故障率计算公式[8]

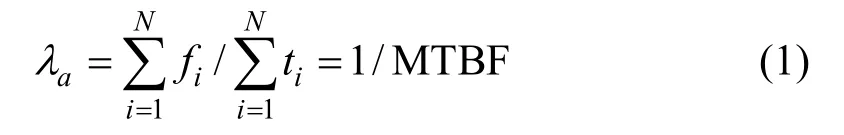
计算，其中fi和ti分别是第i次使用周期中发生的故障数和工作时长。在删除部分奇异数据之后得到长度为1 435 的故障率时间序列作为本文的研究对象，如图1所示。从图中可以看出，原始故障率数据含有大量的噪声，如果不加处理直接用于预测将影响预测结果的准确性。因而为了保证后续预测的精度需要先对原始数据进行去噪预处理。本文采用小波分析作为去噪手段。

1.1 小波去噪原理

利用小波分析进行去噪使用最广泛的是Donoho 提出的阈值去噪法。一个带有噪声的一维信号模型可以表示为

式中：f(t)为含噪信号；s(t)为有用信号；e(t)为噪声；α为噪声强度。小波变换的特点是其具有一种“聚集”的效果：有用信号s(t)的能量会集中于小波域中的少数系数上从而具有较大的幅值，而噪声e(t)的能量会分散到大量的系数上从而对应较小的幅值。因此，必然可以找到某个合适的阈值门限λ，当分解出的小波系数绝对值小于λ时，认为该系数对应噪声，予以消除；反之，则对应有效信号，保存下来。然后再用处理过后新的系数做小波逆变换进行重构即可得到去噪信号。

1.2 去噪结果分析

阈值的选取是整个小波去噪的关键。目前最常用的阈值有4 种：固定阈值、自适应阈值、启发式阈值、最大最小原则阈值。针对本文的故障率数据，经试算，选取dB8 小波进行4 层分解并分别在4 种阈值下对分解系数作软阈值处理，则去噪效果如表1所示。

表1中信噪比(SNR)越大且均方误差(MSE)越小代表效果越好。由表1可知，采用rigrsure 阈值，去噪性能最佳。ATP 故障率时间序列去噪前后对比如图1所示。

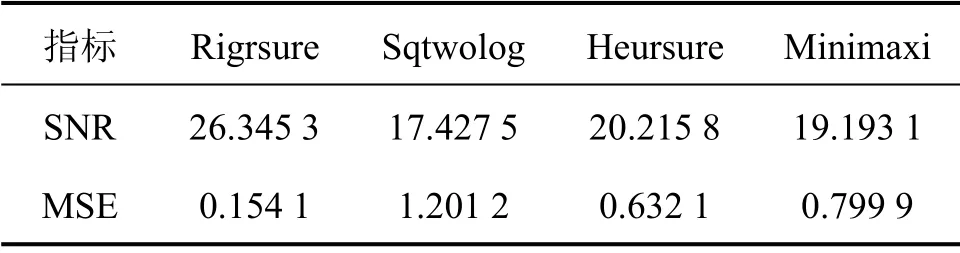
表1 4 种阈值下的去噪效果Table 1 Denoising results under 4 thresholds

图1 去噪前后故障率变化曲线Fig.1 Failure rate curves before and after denoising

从图1可以看出，去噪之后的曲线更为平滑，把去噪后的数据用于后续故障趋势预测可提高预测的准确度。

2 故障率时间序列相空间重构

2.1 混沌相空间重构

由于ATP 设备在日常运行中受到外界多重复杂因素的共同影响，因而其产生的故障率数据具有一定的混沌特性，即整体上遵循某种变化规律但在局部范围内会表现出与随机序列类似的杂乱无章、混乱无序的特点。内在的混沌特性将使得直接在一维空间下从一维故障数据入手进行建模很难真正的挖掘出数据中蕴藏的演化规律。由此，先利用混沌理论的相空间重构技术对本文的ATP 故障率序列做重构映射是至关重要的一步。相空间重构一般采用坐标延迟法：

混沌时间序列{xi|i＝ 1～N}在延迟时间τ和嵌入维数m下重构的m×M相空间为[9]

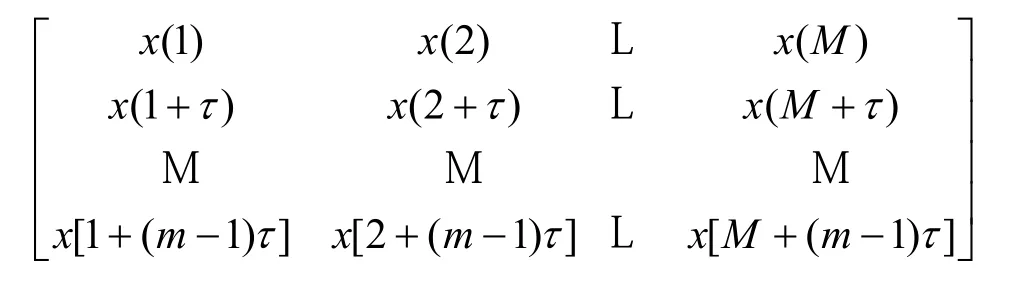
任一相点X(k)＝ [x(k),x(k+τ),…,x(k+ (m-1)τ)]T，M＝N- (m- 1)τ为相点个数。

重构相空间的关键在于选取合适的重构参数延迟时间τ和嵌入维数m。

2.2 C-C 方法计算延迟时间τ

本文采用改进的C-C算法对故障率时间序列进行分析，该算法最早由Kim 等人于1999年提出[10]，其在嵌入窗法的基础上通过计算关联积分同时估计出最优时延τ和嵌入窗宽τw。改进C-C 算法如 下[11]：

设重构后的相点为Xi，定义关联积分

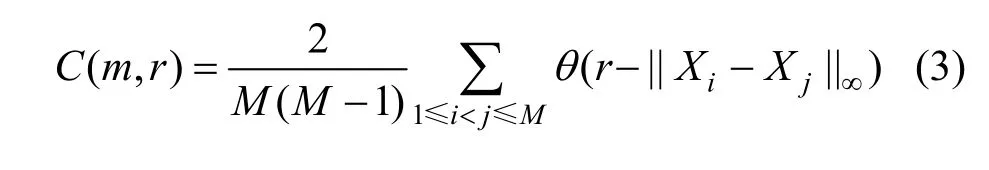
为了计算此统计量，可以把原序列{xi|i＝1,2,… ,N}分解成t个互不相交的子序列，每个子序列的长度为N/t，即：

采用分块平均的策略分别计算每个子序列的统计量再求平均，得

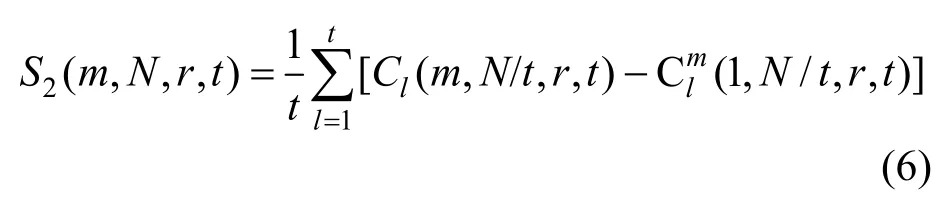
当N→∞时，

定义差量

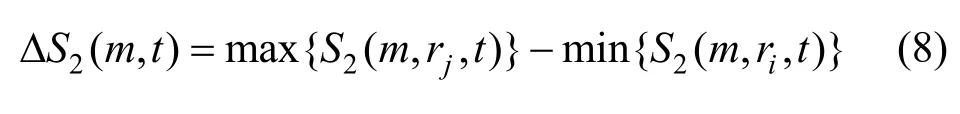
根据BDS 统计结论取m=2,3,4,5，ri=i·σ/2(i=1,2,3,4,σ=std({xi})是时间序列的标准差)，计算如下统计量：

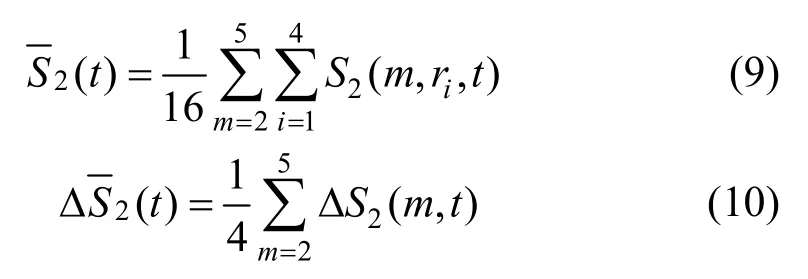
2.3 G-P 方法计算嵌入维数m

目前确定最佳嵌入维数应用最广泛的方法是Grassberger 和Procaccia 于1983年提出的饱和关联维数法(G-P 算法)。根据G-P 算法，C(m,r)和邻域半径r存在以下近似幂指数关系

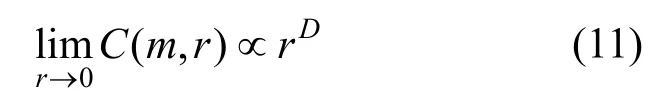
进一步可得

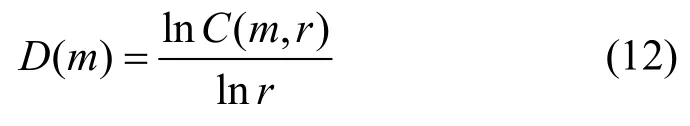
式(12)中的D(m)即为时间序列的关联维数。一般可以先固定m，选择一系列r计算相应的关联积分C(m,r)并在坐标系中画出双对数关系曲线lnC(m,r～lnr)，该曲线线性部分的斜率即为当前嵌入维m对应的关联维D(m)。对于混沌时间序列，D(m)随着m的增大会先增大而后饱和趋于某个稳定值，当D(m)不再发生变化时对应的m即为能够完全展开吸引子结构的最佳嵌入维。

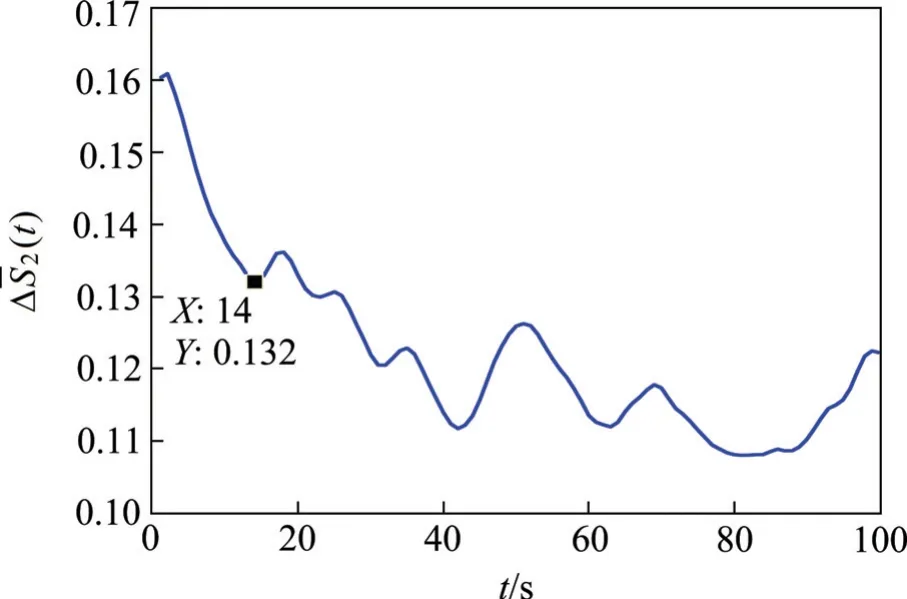
图2 改进C-C 方法求最优时延Fig.2 Computing optimal time delay using improved C-C algorithm

对本文的故障率时间序列应用G-P 算法，计算中使嵌入维数m由1 逐渐增大到14。在求取线性部分的斜率时，选取[ln(0.5σ),ln(2σ)]作为线性区域的范围[12]。具体计算结果如图3所示。

从图3可以看出，当m增加到8 时关联维数出现饱和不再增加，因而m=8 即为最佳嵌入维数，同时这个结果也满足Takens 定理的m＞=2D+1 的条件。

2.4 最大Lyapunov 指数

在求出重构参数后必须对原时间序列的混沌性质进行验证，否则对非混沌时间序列进行重构不仅不能挖掘系统的运动规律反而会破坏系统原有的特征。根据混沌理论，如果一个系统是混沌的，则其对初始条件具有很强的敏感性，即从2 个相邻初始条件出发的邻近轨道之间的距离将随着时间以指数速率分离，这一特点可以用Lyapunov 指数λ来定量描述[1]。1983年格里波基证明了，只要最大Lyapunov 指数λ大于0 就可以确定系统的性质一定是混沌的[13]。

图3 G-P 算法计算嵌入维数Fig.3 Computing embedded dimension using G-P algorithm

本文采用小数据量法计算故障率时间序列的最大Lyapunov 指数，具体步骤如下：

1)求取时间序列的平均周期P。

2)相空间重构，得到相点{X j|j＝1,2,…,M}。

3)寻找每个相点Xj的最近邻点Xˆj，并限制短暂分离，即：

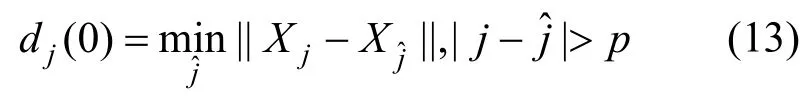
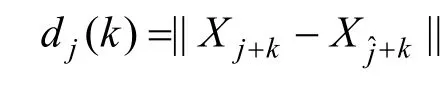
5)对于某个k，对所有的非0d j(k)求平均

其中：q是非0d j(k)的个数，Δt为样本周期。

6)画出y(k)～k曲线，并用最小二乘法拟合曲线的斜率，即为最大Lyapunov 指数λ。

本文故障率时间序列最大Lyapunov 指数求取结果如图4所示。

图4 故障率时间序列最大Lyapunov 指数Fig.4 Maximum Lyapunov exponent of failure rate time series

图4拟合直线的斜率λ=0.011 1＞0，这说明本文的故障率时间序列具有混沌特性，可以通过相空间重构挖掘其蕴藏的变化规律。

3 建立Chaos-Elman 预测模型

本节把混沌相空间重构和Elman 神经网络结合建立Chaos-Elman 故障率预测模型，并以历史故障数据作为样本对模型进行训练，使ENN 在高维重构空间中逼近相点的演化规律，实现对一维故障率时间序列未来变化趋势的预测。

3.1 预测原理及依据

根据混沌理论，相空间中相点的演化行为遵循以下2 条原则[12]：

1)相点X(k)与其邻近相点具有近似的演化趋势。

2)相点X(k)进一步演化为X(k+1)，从而在X(k)和X(k+1)的最后一维分量x(k+ 1 + (m- 1)τ)之间存在某种复杂的非线性映射关系。

基于以上性质，预测原理如下：

一维故障率时间序列｛xi｝(i＝ 1,2,…N)相空间重构后得到高维矩阵[X(1),X(2),…,X(M)]相点X(M)的下一演化点为

可以看出，X(M+ 1)的最后一维分量即为原时间序列的下一个待预测点x(N+ 1)。

根据以上性质，X(M)与x(N+1)之间有着某种确定的函数映射关系，即存在G(·)使得x(N+1)=G(X(M))。为了找到该映射函数，可以先找出X(M)的K个邻近相点X(M j)(j＝ 1,2,…,K)，则这些邻近相点X(Mj)与它们下一演化点X(Mj+ 1)的最后一维分量x(Mj+ 1 + (m- 1)τ)之间存在几乎相同的映射关系G(·)，即

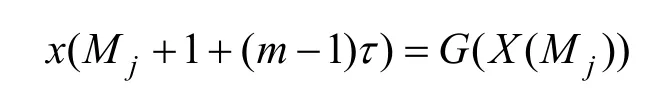
由此，把X(Mj)和x(Mj+ 1 + (m- 1)τ)分别作为Elman 网络的输入和输出进行反复训练，则训练之后的网络就拟合出了此非线性映射函数G(·)，此时再把X(M)作为输入就能够在网络输出端得到预测值x(N+1)。把x(N+1)补充到原时间序列当做已知点按照同样的流程就能得到x(N+2)。以此类推，可对故障率时间序列进行多步递归预测。

3.2 预测仿真结果

在实际仿真预测之前还需要进行以下工作：

1)确定ENN 的拓扑结构。本文故障率时间序列的最优嵌入维为m=8，即每个相点包含8 个元素，因而ENN 的输入层神经元个数为8。根据前文的预测原理可知输出层神经元个数为1。隐含层神经元数量的不同会直接影响到模型的预测精度。经试算，当隐层神经元个数为9 时网络训练误差最小。因此，本文的Elman 神经网络结构为8-9-1。

2)最大可预测时间T。混沌运动的最大可预测时间T=1/λ，如果超过此时间尺度，误差将会迅速放大。本文故障率时间序列的最大Lyapunov 指数λ=0.011 1，从而最长预测时间T=1/λ≈90。基于此，对1 435 个历史数据进行划分，前1 335 个历史数据用于建模和训练，最后的100 个数据作为真实值用于预测对比，以验证模型的预测效果。

数据归一化。归一化公式为

式中：y为归一化结果；x为原始数据，xmin和xmax分别为其中的最小和最大值。

根据以上内容建立Chaos-Elman 预测模型并用历史数据对模型进行训练，同时与不重构直接利用ENN 预测的效果作对比，则短期故障趋势预测结果如图5所示

图5 短期故障率预测结果Fig.5 Short-term failure rate prediction results

本文采用平均绝对百分误差(MAPE)，均方根误差(RMSE)和决定系数(R2)作为衡量模型预测精度的评价指标，则误差计算结果如表2所示。

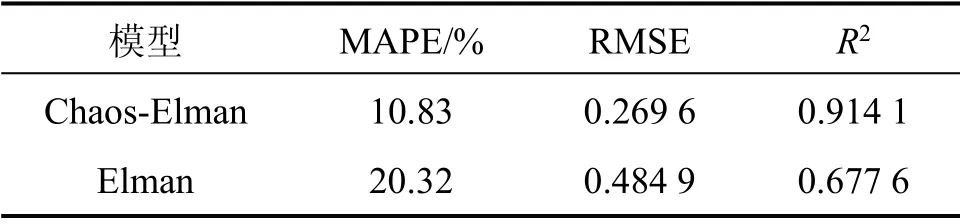
表2 预测误差对比Table 2 Comparison of prediction errors

从预测图和误差表可知，Chaos-Elman 模型的预测效果优于单一的Elman 模型，这说明了由于本文的故障率时间序列具有混沌特性，因而先对其进行相空间重构才能最大程度地挖掘出隐藏的变化规律。把混沌理论和Elman 神经网络结合相比单一的模型能够取得更好的预测性能。

4 MEA-Chaos-Elman 预测模型

Elman 神经网络通常采用BP 算法进行训练，因而具有容易陷入局部极小、过拟合、迭代次数多等缺陷[14]，这些问题会影响网络的训练性能及泛化能力。为了进一步提升故障率的预测准确度，减小预测误差，本文引入思维进化算法(MEA)优化Elman 神经网络的初始权值和阈值以克服网络自身存在的不足，进而在Chaos-Elman 模型的基础上进一步建立MEA-Chaos-Elman 预测模型，使其对ATP的短期故障变化趋势具有更好的预测效果和精度。

MEA是孙承意等[15]针对进化算法存在的早熟、收敛速度慢等问题于1998年提出的一种模拟人类思维活动的优化算法。相比遗传算法的交叉和变异，MEA 最重要的2 个操作是趋同和异化。在系统运行中，趋同与异化同时进行，相辅相成，先利用趋同算子在局部空间内搜索局部最优解，然后利用异化跳出局部空间的约束，在整个解空间中搜索全局最优解，使得MEA 相比其他搜索算法具有更快的收敛速度和更强的寻优性能[15-16]。具体优化步骤如下。

1)将解空间映射到编码空间。编码长度L为

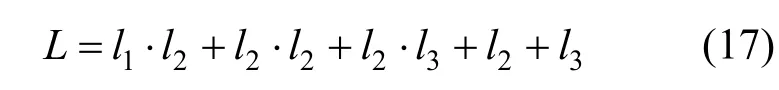
式中：l1为ENN 输入层节点数；l2为隐含层节点数；l3为输出层节点数。

2)设置MEA 算法的参数：迭代次数iter，种群大小pop_size，优胜子群体数目best_size，临时子群体数目temp_size，子群体大小sub_size。

3)选取训练集均方误差的倒数作为个体和子群体的得分函数Score

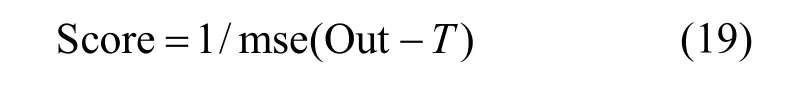
其中：Out 为ENN 的实际输出，T为对应的期望输出。

4)迭代执行趋同和异化操作直至达到全局最优，输出最优个体，并按照编码规则将其解码作为ENN 的最优初始权值阈值再进行网络训练。

按照以上流程建立MEA-Chaos-Elman 预测模型，则优化之后的预测结果如图6所示。

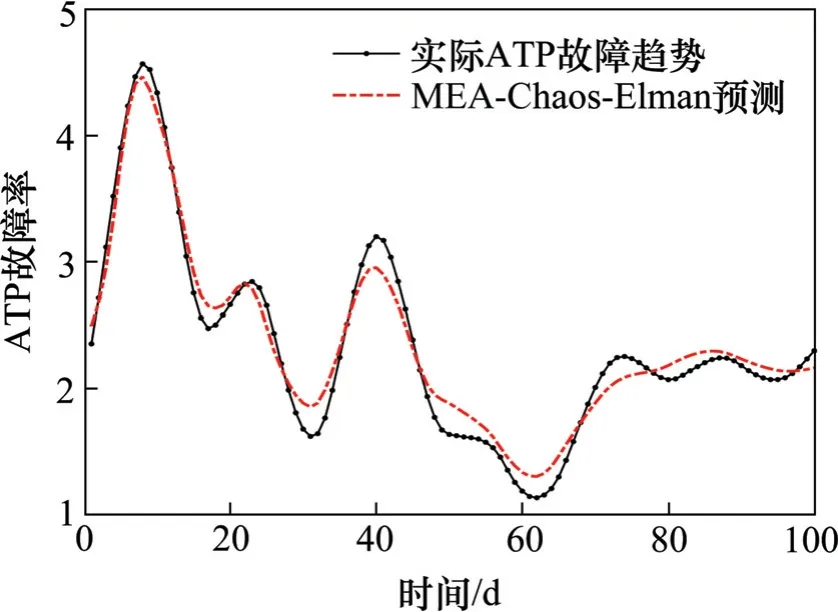
图6 MEA-Chaos-Elman 的预测结果Fig.6 Failure rate prediction result based on MEA-Chaos-Elman model

优化前后预测误差如表3所示。

表3 优化前后误差对比Table 3 Prediction error comparison before and after optimization

可以看出，优化之后的MEA-Chaos-Elman 模型的预测效果明显优于未优化的Chaos-Elman 模型，MAPE/%从10.83%提升到了5.71%，预测值已基本可以吻合实际值，表明所构建的模型是有效可靠的。

5 结论

1)故障率时间序列最大Lyapunov 指数大于0具有混沌特性，可以通过求取重构参数对其进行相空间重构挖掘隐藏的变化规律。

2)把混沌理论和 ENN 结合构建的Chaos-Elman 组合预测模型同时发挥了相空间重构和神经网络的优势，最大程度获取了相点的演化规律等信息，因而其预测效果要优于单一模型。二者相结合大大提升了预测精度。

3)通过MEA 对ENN 的优化结果，证明了MEA 确实提高了网络的整体学习映射能力，使得最终构建的MEA-Chaos-Elman 模型的预测精度达到了95%左右。因而可以利用本文提出的模型对ATP 的未来短期故障率趋势做出较精准的预测以作为铁路相关部门的合理参考依据。