基于机器学习算法的广西桉树适宜性研究
杜雨菲, 吴保国, 陈玉玲
(北京林业大学 信息学院, 北京100083)
桉树Eucalyptus栽培是广西林业生产发展中的优势产业[1]。 作为短周期工业原料林首选的造林树种之一, 桉树效益高、 周期短, 但生长受立地条件影响较大, 规模栽培时需要进行适宜性研究。 树种适宜性研究是当前开展适地适树、 造林决策研究的热点[2]。 王小明等[3]综合了气候、 土壤、 地形等环境因子建立Logistic 回归模型用以确定香榧Torreya grandis‘Merrillii’ 适宜种植区域, 模型检验数据集的总正确率达到了69.8%。 KOO 等[4]基于环境因子, 建立物种分布模型和时间模拟模型研究云杉Picea rubens适生区, 模型验证结果的曲线下面积(area under curve, AUC)达0.99。 胡秀等[5]基于温度、 降雨及海拔等环境因子, 采用MaxEnt 模型软件构建了檀香Sautalum album的适宜性预测模型, AUC 值为0.98。 高若楠等[6]选取立地因子, 利用随机森林模型研究了杉木Cunninghamia lanceolata的适宜性, 模型泛化精度达89.5%。 PIRI-SAHRAGARD 等[7]利用随机森林模型分别探讨了环境因子与白梭梭Haloxylon persicum等5 种植物分布之间的关系, AUC 值总体在0.95 以上。 相较于传统数学建模技术, 物种分布模型和机器学习模型在构建树种适宜性评价模型时效果较好。 目前, 应用于树种适宜性研究的机器学习分类算法层出不穷, 但通过对比分析多种不同的分类算法, 从而进行树种适宜性评价的研究相对较少。 本研究以广西桉树为对象, 使用朴素贝叶斯(naive bayesian, NB)[8]、 支持向量机(support vector machine, SVM)[9]、随机森林(random forest, RF)[10]等3 种机器学习分类算法, 探索立地因子与桉树适宜性之间的关系, 开展树种适宜性研究, 为桉树适宜性研究提供新思路, 为科学造林提供支持。
1 材料与方法
1.1 研究区概况
研究区广西国有高峰林场(22°49′~23°15′N, 108°08′~108°53′E)地处广西壮族自治区南宁市, 属低丘陵山地地带, 平均海拔为200~500 m。 亚热带季风气候, 年平均气温为20.8~21.9 ℃, 年均相对湿度80%以上。 海拔300 m 以下的土壤绝大部分为赤红壤[11]。 地理位置、 气候和土壤条件均十分优越, 有利于亚热带植物的规模化种植。
1.2 数据来源
数据来源于广西高峰林场森林资源规划设计调查数据中的桉树小班数据, 包括立地因子、 林分平均年龄、 优势木平均高。 立地因子包括地貌类型、 海拔、 坡向、 坡位、 坡度、 凋落物厚度、 腐殖质层厚度、 土层厚度、 石砾含量、 成土母质和土壤类型。 地貌类型有低山、 丘陵2 种, 坡向包括东、 南、 西、北、 东北、 东南、 西北、 西南、 无坡向, 坡位包括脊部、 上坡、 中坡、 下坡、 谷地、 平地, 成土母质包括砂岩、 第四纪红土, 土壤类型包括赤红壤、 黄壤、 红壤。 整理数据, 剔除缺失严重记录、 异常数据,得到桉树小班数据1 883 个。
1.3 研究方法
1.3.1 朴素贝叶斯算法 朴素贝叶斯算法是一种基于概率论的机器学习分类算法[8]。 针对桉树小班数据训练集D, 类别集合为yj,y1代表适宜桉树生长,y2代表不适宜桉树生长,ai是待分类的小班, 有a1,a2, …,a11共11 个立地因子。 统计在各类别下各立地因子的条件概率估计值, 即估计第i个立地因子在第j个类别中出现的概率P(ai∣yj), 根据特征独立性假设以及贝叶斯定理, 桉树适宜性分类结果(hnb)可用朴素贝叶斯分类器表示为:

1.3.2 支持向量机算法 支持向量机是一种二分类机器学习算法[12]。 在由立地因子构成的特征空间中寻找1 个分类超平面对桉树小班数据训练样本进行归类(适宜或不适宜), 分类超平面遵循间隔最大化原则。 设有2 类线性可分的样本集合(gi,hi),i=1, …,n;hi∈{+1, -1}; 线性判别函数表示为:

式(2)中: ω 为平面的法向量,b为截距。 通过最大化间隔, 得到最优分类面函数式(3)。 对线性不可分的数据, 也可以通过核函数将其映射到高维空间, 使得样本线性可分。

式(3)中:a*i是不为零的样本, 即支持向量,b*是分类阙值。
1.3.3 随机森林算法 随机森林是一种集成机器学习算法[13]。 采用Bootstrap 重抽样法对桉树小班数据训练集D 进行n次抽样, 得到D1、 D2、 …、 Dn共n个训练子集; 各训练子集分别训练1 棵决策树, 组成随机森林。 在单棵树的训练过程中, 随机选出部分立地因子用以确定决策树的分割节点, 得到n种结果; 使用简单投票法, 得到最多票数的类别或者类别之一为最终的桉树适宜性评价模型, 输出结果见式(4)。

式(4)中:H(x)为组合分类模型;hi(x)为单个决策树分类模型;Y为输出桉树适宜性的变量;I( )为示性函数。
1.3.4 模型评价指标 混淆矩阵(confusion matrix)也称误差矩阵(error matrix), 是评价模型分类效果的常用的指标[14]。 如表1 所示: 混淆矩阵的每一列代表了桉树适宜性评价模型的预测类别, 每一行代表该小班真实的归属类别, 主对角线元素的总和为被正确分类的小班总数(N)。 模型的精度(A, 包括拟合精度和泛化精度)可用小班数与小班总数的比值来表示:

式(5)中:NTP为正类预测为正类的小班数;NTN为负类预测为负类的小班数。 分类误差率(classification error rate)为该类别预测错误的小班数与该类别小班总数的比值, 包括模型对于桉树生长适宜性的分类误差率[式(6)]和不适宜性的分类误差率[式(7)]。 精度、 生长适宜性的分类误差率(ε1)和不适宜性的分类误差率(ε2)通常作为衡量桉树适宜性评价模型判定能力的指标[6]。

表1 混淆矩阵Table 1 Confusion matrix

式(6)和式(7)中:NFN为正类预测为负类的小班数;NFP为负类预测为正类的小班数。
2 结果与分析
2.1 模型实现
树种适宜性评价标准最常用的是地位指数(site index, SI)[6], 各小班地位指数可通过林分平均年龄和优势木平均高得到[15]; 地位指数小于平均值的小班判定为不适宜桉树生长, 大于或等于平均值的判定为适宜桉树生长[6]。 本研究的1 883 个样本数据中, 适宜桉树生长的样本有1 005 个, 不适宜的有878个, 样本量存在一定的不平衡性。 利用机器学习算法解决分类问题时, 数据集不平衡会对模型效果造成影响, 因此需要进行平衡化处理。 在不损失原始样本的前提下, 通过SMOTE 算法[16]对样本构成做平衡化处理, 共得到样本量3 512 个, 其中适宜桉树生长的样本1 756 个, 不适宜的1 756 个; 将实验数据按70%和30%的比例分为训练样本和测试样本, 分别用于模型的训练和测试。
使用naiveBayes( )函数构建朴素贝叶斯模型、 svm( )函数构建支持向量机模型、 randomForest( )函数构建随机森林模型。 3 种模型的输入均为地貌类型、 海拔、 坡向、 坡位、 坡度、 凋落物厚度、 腐殖质层厚度、 土层厚度、 石砾含量、 成土母质, 土壤类型, 输出均为桉树生长适宜性。 利用模型评价指标对比不同模型, 取最优模型确定为桉树适宜性评价模型并进行桉树生长适宜性预测。 对给定立地因子的小班, 将立地因子输入选取的模型, 输出该小班适宜桉树生长的概率, 判断该小班是否适宜桉树生长。 进行立地因子重要性评估, 分析立地因子对桉树生长的影响, 得出适宜桉树生长的立地条件。 桉树适宜性预测模型构建流程如图1 所示。
2.2 模型精度分析
多次训练发现: 朴素贝叶斯、 支持向量机、 随机森林算法构建的桉树适宜性评价模型误差变化均较稳定, 混淆矩阵(表2)拟合精度为63.18%、 69.73%和78.03%, 使用测试数据集对模型进行检验, 混淆矩阵泛化精度分别为64.33%、 67.93%和78.18%。 与朴素贝叶斯、 支持向量机算法相比, 随机森林算法预测精度更高, 可作为桉树适宜性评价的模型。

表2 3 种模型混淆矩阵Table 2 Partial correlation coefficient and its significance test
2.3 桉树适宜性预测
利用随机森林算法构建桉树适宜性评价模型并对桉树进行生长适宜性预测, 预测数据为广西桉树固定样地数据, 各样地的地位指数可通过查阅地位指数表得到[15]。 该数据中桉树的地位指数的平均值为15.09, 将地位指数小于平均值的样地判定为不适宜桉树生长; 将地位指数大于或等于平均值的样地判定为适宜桉树生长。 随机选取5 个样本进行模型验证, 将立地因子输入模型, 输出桉树适宜性概率及适宜性判断结果; 通过与地位指数的比对(表3)可知: 本研究使用随机森林算法构建的桉树适宜性评价模型在实际中是可以使用的。

图1 模型构建流程图Figure 1 Flowchart of model building
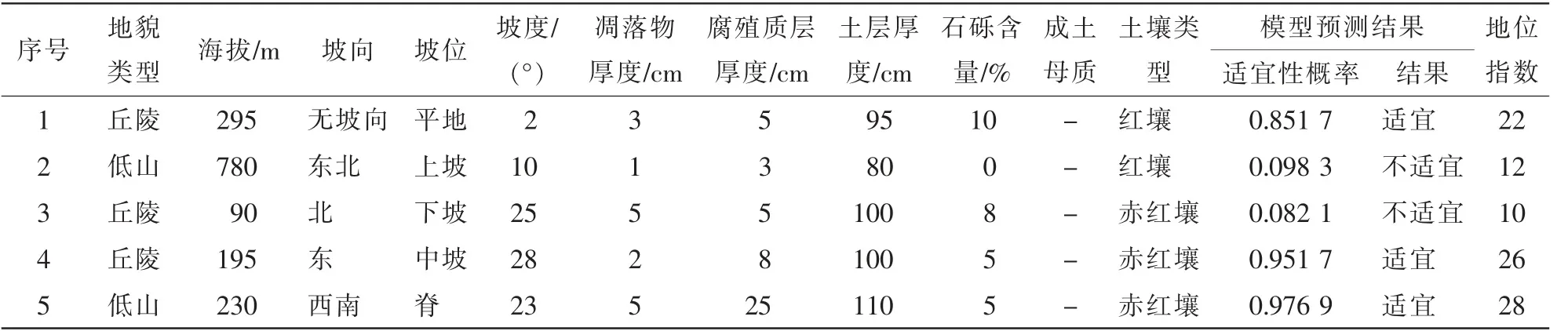
表3 随机森林算法模型判断结果Table 3 Predicted results of random forest models
2.4 立地因子重要性评估
利用随机森林算法对立地因子进行重要性评估[10]。 对某个立地因子j随机取值, 通过评估桉树适宜性评价模型分类准确性下降的程度来评估j的重要性, 分类准确性下降程度越大, 说明j越为重要。 计算方法如公式(8)所示:

式(8)中:Ejr为j的值随机后的袋外(out of bag, OOB)误差,Er为j的值随机前的OOB 误差,NT为分类树的数量。 标准化处理后得到的平均准确度降低程度(mean decrease accuracy, MDA)可用来描述立地因子j的重要性。
对分类树节点作t分割, 计算使用立地因子j前与使用后基尼指数的减小值(DGj), 对所有节点的DGj求和后再对所有分类树NT取平均, 得到平均基尼指数降低程度(mean decrease Gini, MDG)。 MDG 越大, 立地因子j越重要。 基尼指数Gini(t)的计算方法如公式(9)所示。

式(9)中:p(i∣t)为类别i在节点t处的概率,k为分类结果数, 在本研究中取值为2。
使用varImpPlot( )函数对11 个立地因子进行重要性评估。 由表4 可知: 不同重要性评估方法对立地因子的排序结果基本一致; 立地因子的重要性排序由高到低依次为: 海拔、 土层厚度、 坡向、 坡度、石砾含量、 凋落物厚度、 坡位、 腐殖质层厚度、 土壤类型、 地貌类型、 成土母质。

表4 立地因子重要性评估Table 4 Importance assessment of site factors
选取对桉树生长影响最大的2 个立地因子(海拔和土层厚度), 利用随机森林算法进行单因素分析。由图2 可知: 研究区海拔为200~350 m、 土层厚度为80~100 cm 的地区比较适合桉树生长。

图2 海拔、 土层厚度对桉树生长的影响Figure 2 Effects of altitude and soil thickness on growth of Eucalyptus
3 结论与讨论
基于朴素贝叶斯算法、 支持向量机算法、 随机森林算法3 种算法构建的模型拟合精度分别为63.18%、 69.73%和78.03%, 泛化精度分别为64.33%、 67.93%和78.18%; 相较于朴素贝叶斯、 支持向量机算法, 随机森林算法对缺失数据不敏感, 在训练的过程中能检测到特征与特征之间的互相影响, 模型泛化能力强, 具有更高的预测精度, 在本研究中分类效果最好。 缺少特征独立性假设和立地因子数据是朴素贝叶斯算法分类效果差的原因; 而缺少通用的解决方案, 对缺失数据敏感, 受核函数的影响较大等导致了支持向量机算法分类效果欠理想。 本研究采用的多模型对比为以后其他树种适宜性研究选取模型提供了参考。
海拔、 土层厚度、 坡向、 坡度等立地因子对桉树生长影响较大, 地貌类型、 成土母质等则较小。 原因可能是海拔高度、 坡向、 坡度的改变造成空气温度、 空气湿度、 太阳辐射等变化[6], 从而影响桉树生长; 土层厚度与土壤养分、 矿元素等密切相关[17], 研究区的桉树种植区域, 地貌类型和成土母质均比较单一, 因此对桉树生长的影响并不明显。 对海拔、 土层厚度等立地因子的单因素分析发现: 桉树适宜生长地区多数海拔为200~350 m, 土层厚度为80~100 cm。 研究认为[18]: 海拔高度低于350 m, 桉树径生长随海拔升高而增粗, 当海拔大于350 m, 环境热量不足桉树容易引发低温冻害[19]。 土层厚度对桉树的影响体现在土壤的营养状况和给树木生长提供的养分上[17], 本研究发现土层越厚, 土壤营养条件越好,也越适宜桉树生长。 总的来说, 不同的立地因子对桉树生长的影响程度不同, 选择桉树种植区域时应客观考虑各个立地因子的影响程度, 从而合理地调整立地条件的组合, 最大程度满足桉树生长。
基于机器学习算法构建的树桉树适宜性评价模型可以较好地对桉树的适宜性做出预测, 为科学造林提供依据。 树种适宜性分析不仅要将立地分为适宜该树种生长以及不适宜该树种生长, 还可以进一步对其进行细分, 从二分类问题转变为多分类问题, 进一步研究机器学习算法在树种适宜性分析中的应用。

