纵向通风对地铁区间隧道火灾温度特性影响

易欣，范晶，马砺，杨元博，张鹏宇

(1.西安科技大学安全科学与工程学院，陕西西安，710054；2.西安科技大学陕西省煤火灾害防治重点实验室，陕西西安，710054)

地铁属于地下半封闭的空间，一旦发生火灾，由于内部空间相对狭长，逃生条件差，疏散救援困难将造成大量的人员伤亡[1]。同时，火灾形成的高温气流超过隧道承载能力时，隧道结构将遭到破坏[2]。此外，地铁火灾的类型多样化，主要包括区间隧道内电缆火灾、车厢内饰及乘客行李火灾、机车电气设备火灾等[3]，其中，区间隧道发生火灾时火灾规模一般较大，而且列车在行进过程中，火灾对人员影响更为严重。国内外对隧道火灾温度分布理论研究中包括顶棚最高温度和顶棚温度水平分布2方面，主要采用小尺寸实验、数值模拟和理论分析结合的方法进行研究。SHAFEE等[4]通过实验，研究得出隧道纵向通风、热释放速率及隧道阻塞等是影响顶棚温度及其分布的主要因素，其中纵向通风影响因子为45%、隧道堵塞影响因子为25%，隧道倾角影响因子为19%，其他因素影响因子为11%，没有堵塞的情况下，热释放速率约增加33%。隧道纵向通风、火源功率及隧道阻塞等因素是学者研究顶棚最高温度及其分布的要点。ALPERT[5]根据大量实验测试研究了无限大平板下热烟气最高温度与距离的关系，提出Alpert顶棚射流烟气温度预测模型。KURIOKA等[6]实验得到隧道顶棚最高温度和火源功率以及纵向通风的预测模型，该模型认为最大顶棚温度与量纲一功率和弗洛德数有关。HU等[7]通过实验和数值模拟对Kurioka公式进行一致性验证，通过小尺寸实验和理论推导最高温度关系式，得出顶棚温度在水平距离上的衰减过程呈指数关系。翁庙成等[8]通过实验研究也发现隧道顶部上游的烟气温度纵向分布服从指数衰减规律，同时提出烟囱效应也会对烟气流动存在影响。TIAN等[9]实验发现火源功率和通风速度对顶棚最高温度及其位置影响明显。INGASON等[10]利用小尺寸模型提出一种基于指数关系的火源下游的温度分布公式，解释了最大顶棚温度沿着隧道延伸现象。LI等[11-12]在Kurioka公式的基础上考虑了隧道放热速度、纵向通风速度和截面形状的影响，研究表明：在当通风速度(量纲一的量)大于0.19时，隧道顶棚下最大升温随纵向通风速度线性减小，其余情况下，则随放热速率(量纲一的量)的2/3功率变化。KHATTRI[13]对该结果进行了实验验证。FAN等[14]对火灾附近横向烟气温度分布及其与纵向烟气温度分布的差异进行比较，建立了顶棚下横向烟气温度分布的相关关系，认为隧道侧壁的阻挡作用使得温度的横向衰减速度增加。然而，GONG等[15]通过小尺寸实验和理论分析研究了隧道烟气传播过程中传热传质问题，提出关于温度在水平分布的非齐次线性微分方程，该结果显示温度分布并非遵循指数关系。国内外学者在隧道温度分布的研究较多以公路隧道为模型，以小尺寸实验和数值模拟为主要实验手段，温度分布的理论预测模型研究最为广泛，但提出的关系式存在较大差别，主要原因是实验模型、通风速度、火源功率的选取与地铁区间隧道实际参数存在差距。例如，翁庙成等[8]采用1:10实验模型，火源功率为1.59～12.38 kW进行实验，得到的预测结果比Hu模型的大；LI等[12]采用矩形和圆弧隧道截面进行实验研究，通风速度为0.05～0.72 m/s，火源功率为1.1～14.0 kW，预测结果与通风速度关系较大，实验功率低于实际火灾功率；刘方等[16]对不同截面形状进行研究，结果表明：仅当截面形状系数小于1时，温度分布服从指数衰减规律，反之，需进行系数修正。王君[17]发现隧道坡度和预测修正系数存在对应关系，对Hu模型的预测结果进行修正。在此，本文作者建立1:10小尺寸实验台，针对区间隧道的截面和火灾规模研究不同纵向通风速度条件下火灾发展过程及规律，主要包括纵向通风速度、火源功率对温度分布和烟气流动的影响，为进一步研究区间隧道火灾的规律和火灾扑救及人员救助等方面提供理论依据。

1 实验设计

1.1 理论分析

为了研究方便，进行如下假设：

1)火源为固定式火源；

2)火灾烟气运动满足Boussinesq假设，即ρ0-ρ≈ρ0β(T-T0)，其中，ρ为流体密度，ρ0为参考位置的流体密度，β为体积膨胀系数，T为气体温度，T0为参考位置的气体温度；

3)火灾烟气为不可压缩流体；

4)固壁传热为一维热传导；

5)不考虑由于化学反应引起的烟气成分变化。

根据Froude相似性原理，得到各参数关系式如表1所示。

表1 地铁烟气运动相似关系Table 1 Scaling relations of smoke movement

1.2 实验台设计

本研究模型取自西安地铁三号线某区间隧道，选取长度100 m作为研究区域，采用1:10比例建立小尺寸模型。隧道截面宽度为0.48 m，高为0.42 m，顶部为拱形结构，半径为0.24 m，底部为矩形，高为0.18 m，由单节长度为0.7 m的14根节段连接而成，隧道长共为10 m，隧道一端安装轴流风机，另一端为自然排烟。实验台布置图如图1所示。

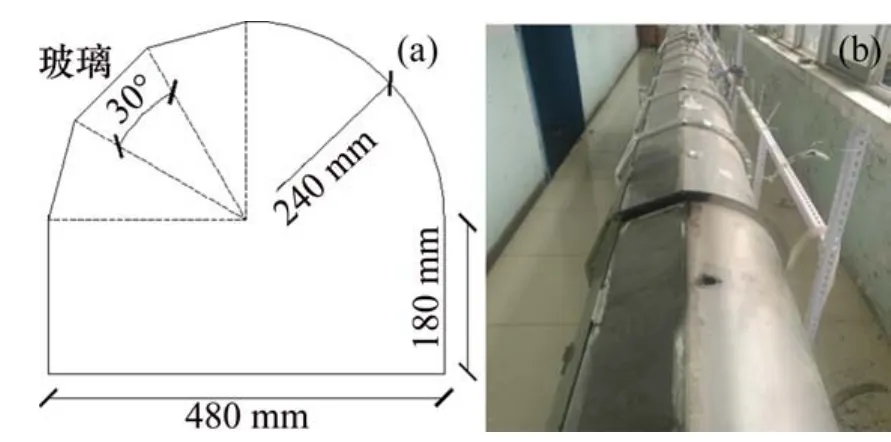
图1 1:10小尺寸实验台Fig.1 Photos of 1:10 model-scale tunnel

1.3 火源设计

火源功率Q是指单位时间内可燃物燃烧释放出来的热量，决定了室内温度和产烟量，计算式如下：

式中：φ为燃烧效率因子，反映不完全燃烧的程度，取0.3～0.9；m为可燃物质量燃烧速率；ΔH为可燃物的热值，kJ/g。

根据王建文等[18]的研究结果，行李的热释放速率不超过2 MW，通风条件下，车厢热释放速率约为3.9 MW。本实验采用柴油作为燃料，燃烧热约为42 kJ/g。易亮等[19]认为柴油油池火燃烧过程分为3个阶段，每个阶段均占全过程的1/3，其燃烧效率为0.68～0.85，主要受燃烧面积和通风条件的影响，燃烧速率处于16～38 g/(s·m2)之间，当火源面积为0.25 m2时，燃烧速率为 16.4 g/(s·cm2)。王君[17]对较小尺寸油盘燃烧速度进行测定，得到燃烧速率为1.0～1.4 mg/(s·cm2)。FERRERO 等[20]对直径为3 m的油盘中柴油燃烧速率进行计算，得稳定燃烧阶段的柴油燃烧速率约为39 g/min，即2.2 mg/(s·cm2)。本实验采用油盘半径为10，11和12 cm，油盘面积较小，故取燃烧速率为1.2 mg/(s·cm2)，燃烧效率为0.8。不同直径油盘火源功率如表2所示。

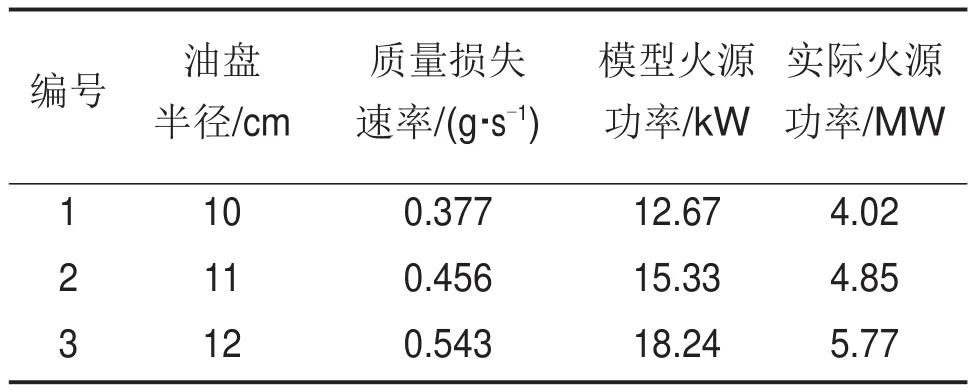
表2 不同直径油盘火源功率Table 2 Heat release rate(HRR)for reduced and full scale

2 实验工况

为研究火灾时隧道模型空间内的温度场分布和热辐射，采用K型铠装热电偶测定场内温度分布、采用热流计测定不同位置的热辐射强度，采用电子风速仪测定风速。

根据地铁设计规范，隧道区间排烟速度应大于2 m/s，小于11 m/s。根据相似性比例设置实验工况如表3所示。火源下风侧温度测点布置图如图2所示。

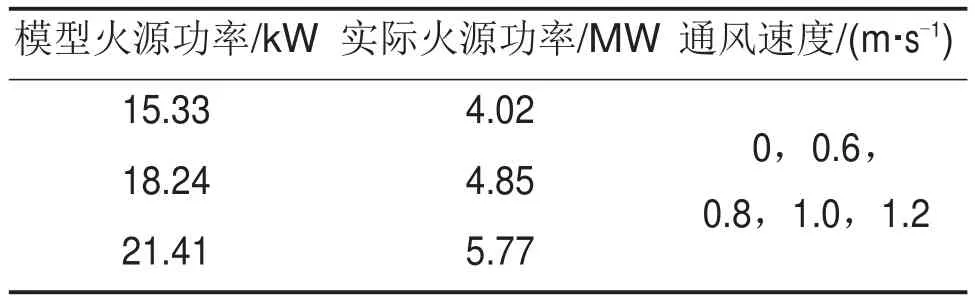
表3 实验工况设置Table 3 Key parameters of test cases

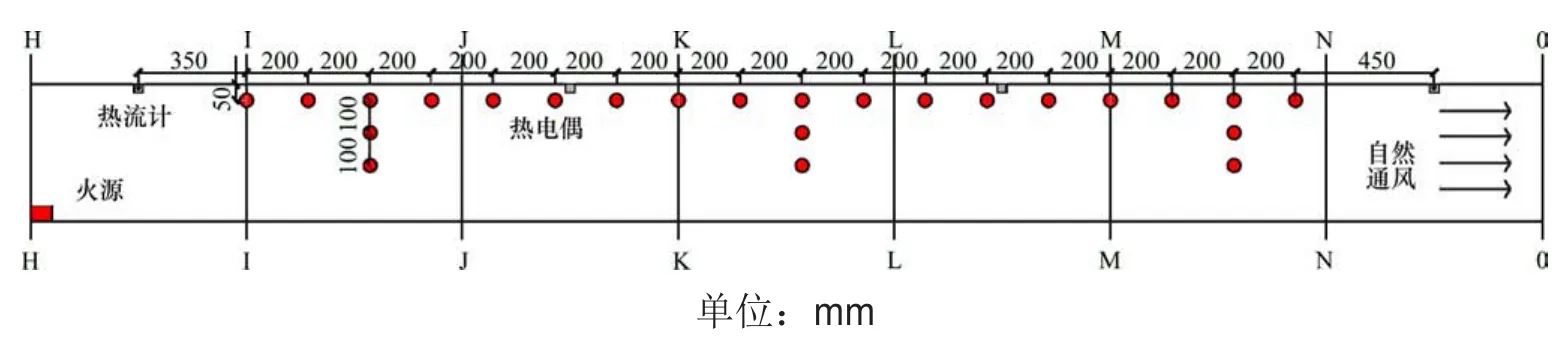
图2 火源下风温度测点布置图Fig.2 Thermocouple arrangement on fire source downstream side

3 实验结果分析

3.1 通风速度对火焰形状的影响

在区间隧道火灾发展过程中，火源功率和通风速度对火焰形状有明显的影响。通过油盘实验，对实验过程中燃烧稳定阶段的火焰形状进行观察，实验结果如图3和图4所示。

从图3可以看出，火焰发展过程中，当无纵向通风时，火源静止燃烧，火焰竖直向上，同时，由于空间有限，油池燃烧不充分，火焰宽度较小。随着纵向通风的增加，通风加强，火势增大，火焰长度和火焰倾角明显增加，火焰高度逐渐降低。由图4可以看出，通风风速相同时，随着火源功率的增加，火焰面积增加，火焰燃烧越不充分，火焰颜色由亮黄色变为深黄色，燃烧效率降低，产烟量增加。因此，当增加纵向通风时，会加强火焰燃烧，降低火焰高度。

3.2 顶棚水平温度分布

当火灾发生时，由于火羽流的浮升力作用，烟气向上蔓延，受到隧道顶部阻挡后形成顶棚射流，烟气沿着隧道顶部纵向流动，同时在重力作用下向下运动。因此，顶棚温度能够反映出隧道内最高温度，研究顶棚温度分布对人员疏散均具有重要意义。不同火源功率下纵向通风风速对顶棚烟气温度分布的影响如图5所示。

由图5可知，当无隧道通风时，火源两侧温度近似正态分布，火焰正上方温度比其他位置的高，且随着火源距离的增加，烟气温度下降缓慢。3种火源功率下最高温度分别为235，294和475℃，火源功率增加，燃烧加剧，顶棚最高温度增大。当增加纵向通风风速时，火源两侧温度显著下降，当风速大于1.0 m/s时，对温度的下降过程影响不大。火源上风侧(大于0.7 m)的温度和环境温度一致，烟气没有造成火源上风侧的温度升高，表明该风速条件对温度和烟气有良好的控制效果。由于隧道相对封闭导致由对流产生的热交换速度降低，增加风速仅提高了顶棚烟气流动速度，对烟气温度降低效果较小，此时，全尺寸模型的实际风速约为3.33 m/s。在距离火源位置大于2.5 m时，纵向通风速度对隧道温度影响不明显。

为进一步研究隧道火灾纵向通风时温度分布的规律，对不同风速下的最大温差进行曲线拟合，结果如图6和表4所示。由图6和表4可知，最大温差与位置呈指数关系。风速越小，火源功率越大，拟合结果越指数关系接近。当风速为1.0 m/s时，最大温差接近于定值，3种火源功率下的最大温差分别为50，55和100℃。产生该现象的主要原因是风速的增加已经无法造成更多的对流传热损失。

3.3 顶棚温度（量纲一的量）分布

在温度分布的研究中，HU等[7]通过理论分析和实验研究，得到了温度分布的理论公式：

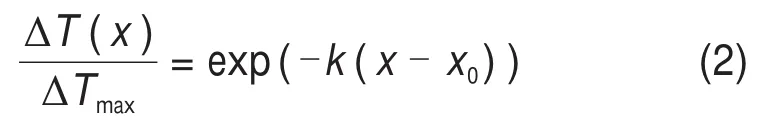
式中，x为火源距离；ΔT(x)为x处相对环境温度的温升；ΔTmax为参考位置x0处烟气层相对于环境温度的温升；k为烟气层温度纵向衰减系数。

考虑到空气的影响，INGASON等[10]利用小尺寸模型研究提出如下模型：

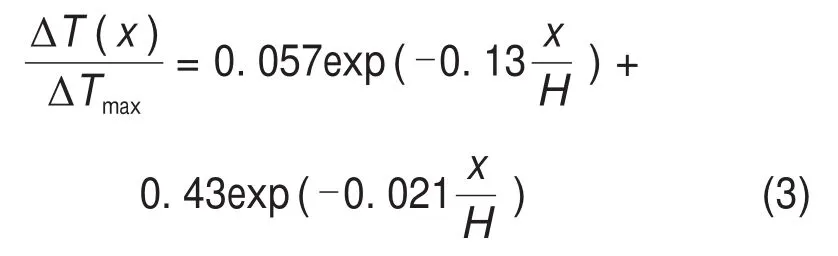
式中，H为隧道内部拱顶高度。

KHATTRI[13]在此基础上利用数值模拟方法进行验证，提出如下模型：

图3 火焰形状随通风速度变化图(Q=12.67 kW)Fig.3 Shape of flame varies with velocity of ventilation(Q=12.67 kW)

图4 火焰形状随火源功率变化(v=1.0 m/s)Fig.4 Shape of flame varies with power of source(v=1.0 m/s)

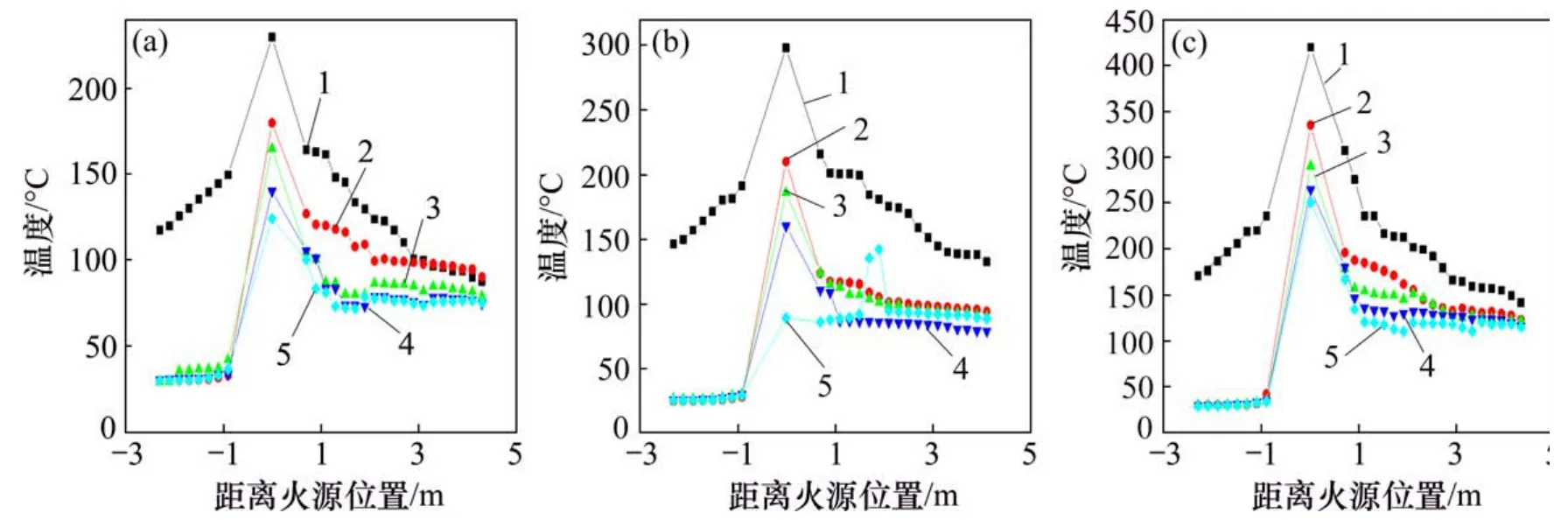
图5 不同火源功率下纵向通风风速对顶棚烟气温度分布的影响Fig.5 Maximum ceiling smoke temperature distribution with various ventilation under different fire powers

图6 不同火源功率下纵向通风风速对顶棚温度变化拟合Fig.6 Fitting diagram of ceiling temperature distributions in various ventilation under different fire powers

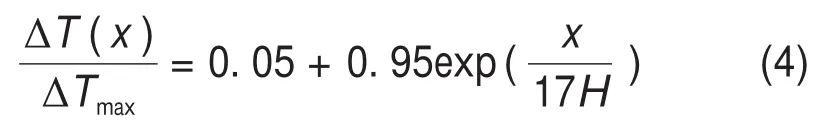
温度随火源距离(量纲一的量)分布主要呈现指数关系[6]。为对区间隧道顶棚最高温度进行数学化描述，对温度和火源距离进行量纲一化，3种火源下的拟合曲线如图7所示，其中，L为模型高度。由图7可知，当实验风速较大时，最大温差的分布与火源位置的相关性减小。

为研究最不利通风条件下的温度分布，即纵向通风风速为0 m/s，对3种火源下的温度进行拟合，得到拟合的温度分布为

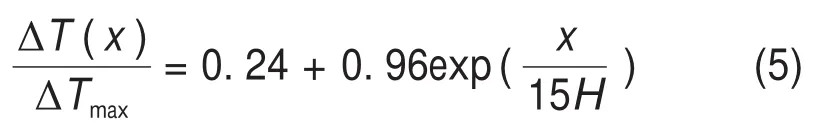
3.4 顶棚热辐射变化

在隧道纵向通风的条件下，火焰水平延展长度为0.3～0.5 m，实验中在火源下风侧0.35 m处顶棚位置布置热流计，得到实验结果如图8所示。

由图8(a)可知，隧道内热辐射随时间变化呈正态分布，同时，当隧道内无纵向通风，顶棚热流量显著增加。纵向通风风速增加至一定值后，风速的增加对顶棚热流量影响较小。当Q=12.67 kW时，无风条件下的热流量最大值为风速1.0 m/s时的6倍。

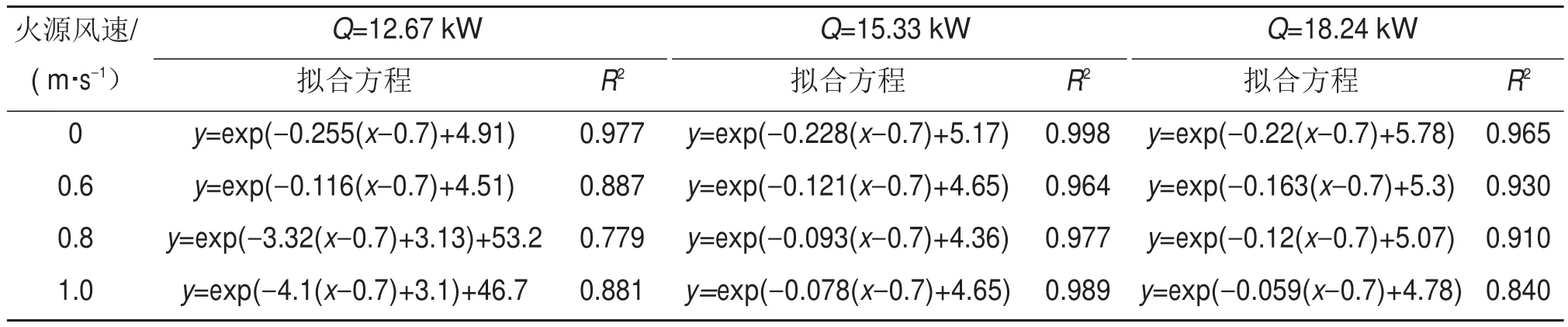
表4 不同火源功率温度分布拟合结果Table 4 Fitting results of ceiling temperature distribution of different fire power

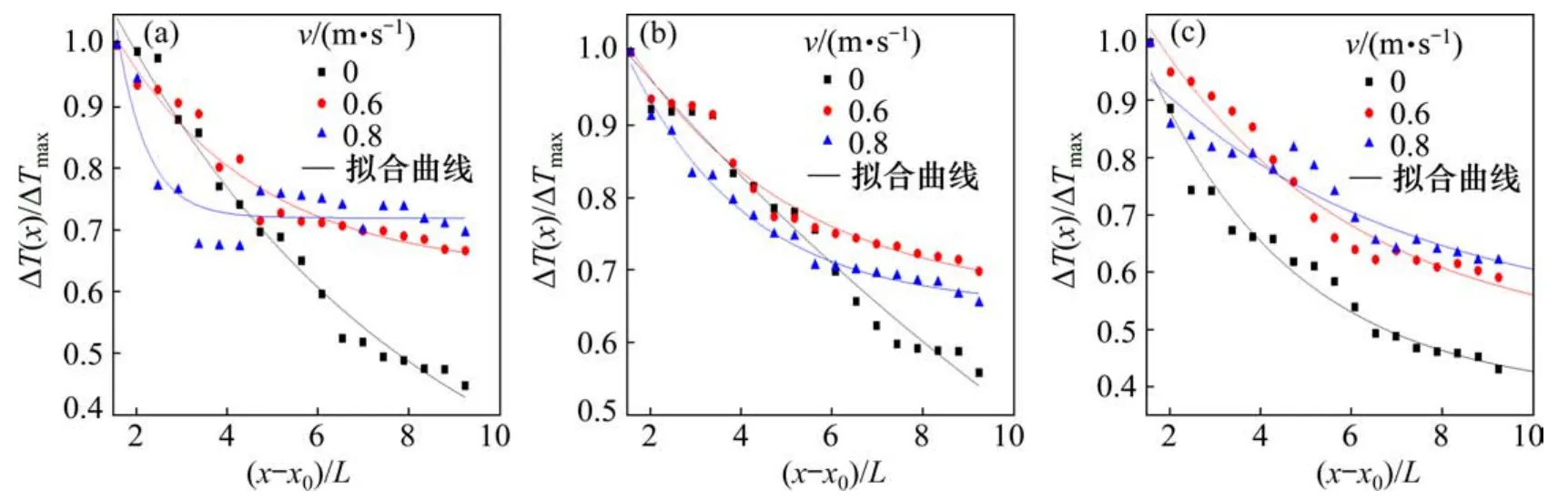
图7 不同火源功率下纵向通风风速对顶棚温度(量纲一的量)分布图Fig.7 Distributions of dimensionless ceiling temperature in various ventilation under different fire powers

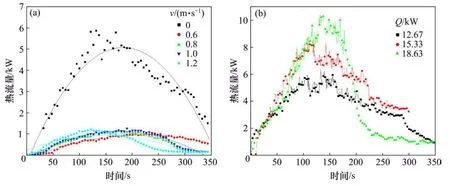
图8 不同纵向通风和火源功率时的顶棚热辐射Fig.8 Flux varies with different ventilation and fire powers

由图8(b)可知，当隧道内无纵向通风时，3种火源功率下的热流量变化趋势基本一致，最大值分别为9.6，7.8和6.0 kW，约为火源功率的一半。

4 结论

1)对于固定火源，增加纵向通风会加强火焰的燃烧，使燃烧更充分，火焰长度增加、火焰高度、隧道内顶棚的热辐射和温度降低，当隧道纵向通风风速大于1.0 m/s时或者当距离火源距离大于2.5 m时，降温效果不明显。

2)火源功率是影响辐射强度和顶棚温度的重要因素，火源功率越大，对隧道产生热辐射越强。无通风条件下顶棚最大温度(量纲一的量)与火源功率呈指数关系，随着纵向通风风速增加，二者相关性逐渐降低。

3)当风速为1.0 m/s时，对温度和烟气有良好控制作用。根据相似性原理，当实际地铁区间隧道火源功率小于6 MW时，纵向通风风速设定为3.3 m/s能有效控制烟气向下风侧蔓延，同时能有效降低隧道纵向温度和辐射强度。