酒业配送系统多设施选址模型研究—以伊力特公司为例
塔斯肯·吐尔汗别克,王海灵
(新疆大学 经济与管理学院,新疆 乌鲁木齐 830046)
1 引言
最近几年,国内白酒行业销售收入虽然在上升,但同比增长率却有所下降。2018年白酒行业销售收入飙升至5 364 亿元[1],但其销量缩小。如要保证企业的盈利不减,减少物流配送总成本是不可或缺的路径,即优化厂址、配送中心与客户群之间的配送系统网络关系。
伊力特实业股份有限公司(简称伊力特、股票代码:600197[2])被誉为“新疆第一酒”。由于水资源对酒厂选址是强约束,多分布在偏远地区,往往形成逆向配送系统网络结构,配送系统总成本高,减少公司利润。因此需要对配送系统网络进行优化,才能保证伊力特公司“新疆第一酒”的区域性品牌,以及上市公司的盈利保证。即从厂址、配送点、客户群之间的网络关系进行多设施选址优化,目的是要找到伊力特在这种市场减弱情况下的配送优化方案。
多设施配送中心选址可以帮助企业优化产品销售的空间布局,从而使得企业降低成本,提高利润,增强综合竞争力,但在整个研究过程中,不同的企业、不同的产品、不同的区域,具有特殊性和差异性。
2 文献综述
2019年9月19日在CNKI分别以“多设施选址问题、模型、建模及求解方法”为关键词搜索,总篇数为641,具体的文献数见表1。
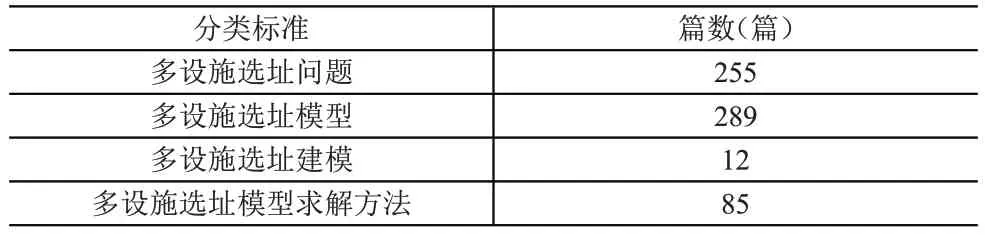
表1 有关多设施选址的中文文献统计表
同时用关键词“设施选址(食品、饮料、红酒、啤酒、白酒)”查找到的有关文献见表2。

表2 有关食品、饮料、红酒、啤酒、白酒设施选址的中文文献统计表
2.1 国内文献综述
目前设施选址所研究的方向是单一的,杨赟[3]对物流系统的选址定位于企业物流战略层,它决定了整个物流系统及其他层次的结构,供应链系统上的核心企业选址决策直接影响所有参与组织的选址决策。肇先和薛敬静[4]归纳总结出常用的6种选址方法。詹庆明和杨爽[5]在设施选址中指出优化的必要性,并对设施选址优化进行了详细的研究。韩霜[6]在关于物流网络的优化中专注研究物流成本。随着配送系统网络选址优化时间及空间复杂性的提高,影响设施选址的因素也变得越来越复杂,人们对设施选址优化精度越来越高,因此增加了设施选址的模型构建、求解及评估优化的难度。本文以配送系统网络总成本最小为目标,构建其多设施选址模型及总成本评价,使得该论文具有很好的实用价值。
构建多设施选址模型的方法主要是整数规划法[7]的拓展及变形,混合整数规划模型[8]为主要类型。黄凯明、卢才武和连民杰[9]在3E-LRP研究中,综合考虑工厂、中心仓库、区域配送仓及零售商的三层路径规划,寻找两层设施选址和三层路径规划的系统最优方案。张金凤[10]建议配送系统网络选址以使配送中心的投资额及运输费用和最小为目标。多设施选址模型的求解方法主要有遗传算法[11]、启发式算法(贪婪加入算法和贪婪去除算法)[12]、仿真模拟法、分布估算法、禁忌搜索法、粒子群优化算法、量子进化算法。
2.2 国外文献综述
同一时间在百度学术以“Multi-facilitiy Location”为关键词搜索,查找到外文文献191篇。最新的与本研究相近的文献有5篇。
M.Hakan Akyüz,Temel Öncan和I.Kuban Altinen[13]研究的多商品多容量多设施韦伯问题是为了满足j 个顾客对k 个商品的需求,使总运输成本最小化。Poudel S R,Marufuzzaman M 和Bian L[14]在研究中提出了一个数学模型,设计一个可靠的多式联运网络供应链系统,同时考虑站点相关的设施故障和拥塞。所提出的模型定位多模态设施,并确定最优生产、存储和路由计划,以使整个系统成本最小化。Li S和Huang Y[15]研究中考虑到不是每个网络上的节点将同样可能作为一个需求节点,他们明确地将概率整合到基于多径站模型中,以确定最佳站位置,以提高系统级上所有需求节点的期望总覆盖率,得到混合整数线性规划模型,提出了一种基于遗传算法的启发式算法,克服了计算上的挑战。Heyns A M 和Van Vuuren J H[16]在研究中介绍了一种新的数学处理方法(非支配排序遗传算法II 算法),用来解决多类型、多区域设施选址问题。Tan B、Ma H和Mei Y[17]在研究中用基于粒子群优化的算法解决多目标优化问题。
因此,关于酒业配送系统多设施选址模型的研究较鲜见。
3 配送网络结构、建模、实证及实证分析
3.1 配送网络结构
在配送网络规划中,已经确定了b个供应点、c个仓储配送中心、d个需求点,要求产品在c个仓储配送中心进行分配,即产品由b个制造厂经c个配送中心配送至d 个市场区域,要得到最佳的配送中心,使总成本最小,其决策问题的约束条件见表3。

表3 配送网络建模假设
网络结构示意图如图1所示。

图1 配送网络结构示意图
3.2 配送网络建模
目标函数为整个配送网络中的总成本最小,建立的模型如下所示;
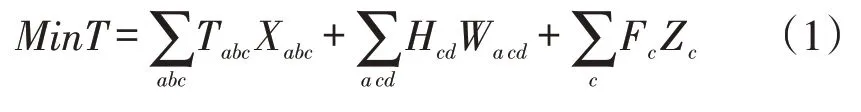
约束条件如下:
不能超过工厂的生产能力:

配送中心容量限制:

进出配送中心c的产品a的数量相等:

满足所有客户需求:

每个客户只能由一个配送中心提供服务:

上述公式中字母的含义如下;
a:产品a;
b:工厂b;
c:配送中心c;
d:客户d;
Xabc:从工厂b运送到配送中心c的产品a数量;
Wcad:经配送中心c 运送到客户d 的产量a 数量;
Cabc:a 产品从工厂 b 送至配送中心 c 的单位生产成本、运输和仓储操作成本;
Hcd:单位产品从配送中心c 到客户d 的运输费用;
Sab:b工厂生产a产品的最大生产能力;
Mc:c配送中心的最大储量;
Dad:d客户对a产品的需求量;
Fc:配送中心的年固定成本;
Zc:0-1规划变量,若使用c配送中心为1,否则为0;
Ycd:0-1规划变量,若c 配送中心为d区客户服务为1,否则为0。
3.3 实证及实证分析
3.3.1 实证。伊力特公司原配送系统网络如图2所示,生产能力、实际生产、单位生产成本和总生产成本见表4,区内各个地区配送点的成本与容量数据见表5,总库至各配送点距离和运输成本见表6。

表4 伊力特公司的生产能力、实际生产、单位生产成本和总生产成本

图2 原伊力特配送系统网络分布示意图

表5 伊力特公司疆内各个地区配送点的成本与容量数据
所有表格中只做公路运输成本计算(公路运输成本为0.35元/t·km),不考虑其他运输方式。
满足原配送模型建立的约束条件,利用模型解出的总成本为:

新配送网络如图3所示。优化后的DC 运输、仓储搬运、固定成本及仓储能力见表7,各客户群的需求能力和运输成本见表8。
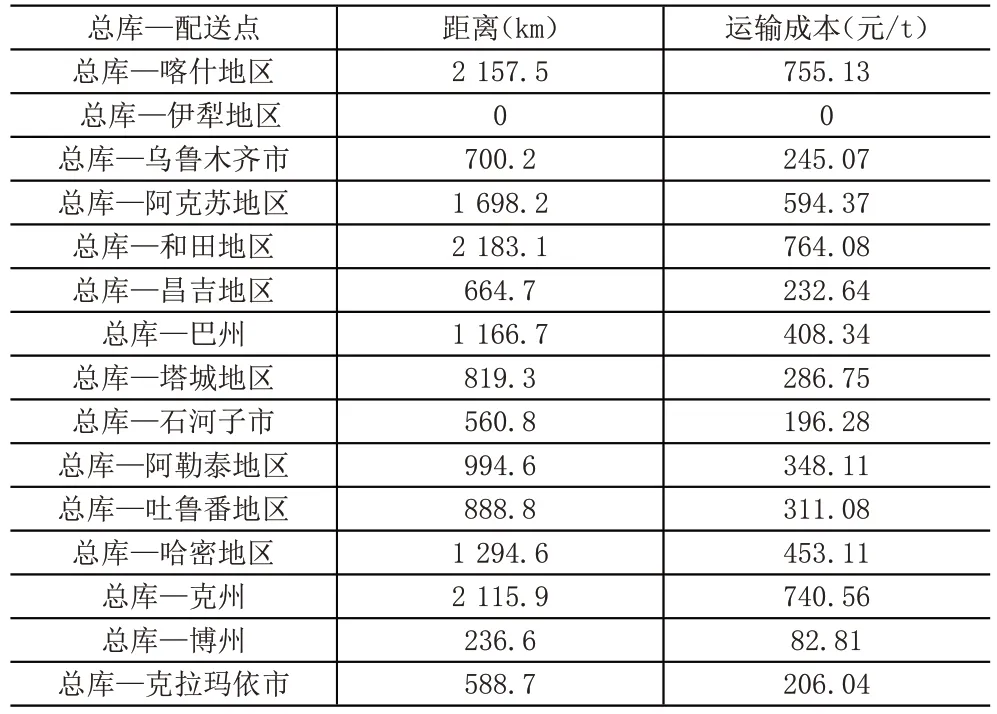
表6 总库至各配送点距离和运输成本

图3 优化后的配送系统网络结构示意图

表7 优化后的DC运输、仓储搬运、固定成本以及仓储能力
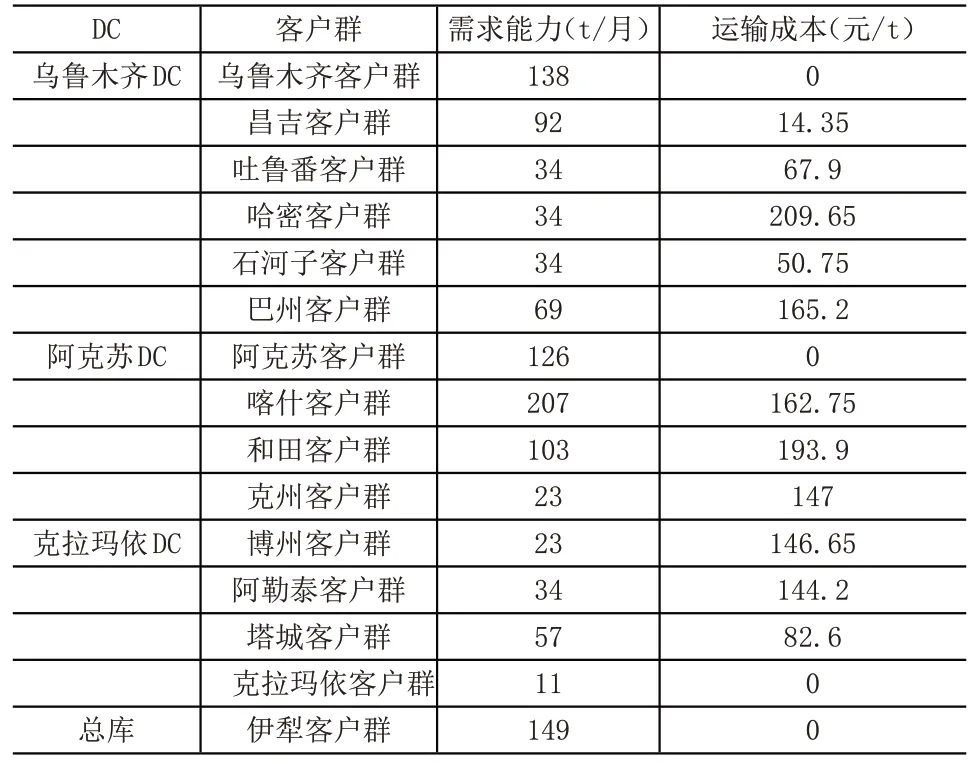
表8 客户需求能力和运输成本
满足新建配送模型建立约束条件,利用模型解出的总成本为:

3.3.2 实证分析。通过新配送系统网络与原配送系统网络比较,新配送系统网络的总成本比原配送系统网络可节约成本4 044 192.19元,新配送系统网络每月能降低伊力特公司总成本的7.5%左右。新配送系统网络中每个要素及各要素之间对系统总成本的影响关系为:
(1)从图2与图3配送网络结构图比较可知,原配送网络(图2)中总厂和分厂的产品需要存到总库,属于点到点配送。优化后的新配送系统网络(图3)把总库到15个地州的配送网络优化成总库到3个区域配送系统网络及生产所在地客户群,然后再由每一个区域配送系统网络配送到该区域科学合理覆盖范围的客户群。因此,原有的15 个配送点减少到3个,节省了12个配送点的造价成本或租用成本,每月可节约成本约4 034 000 元,占节约总成本的99%的费用。
(2)原配送网络中的每一个地州配送网络都有单一的客户群,而新的配送网络构成一个网络客户群,并建立了一个扇形或圆形的合理配送网络体系,从而提高了整个网络的协同协调效应。
(3)新配送系统网络的运输距离与原配送系统网络的距离基本没变。但优化后的配送系统网络可以提高运输车辆的满载率和降低空载率和车辆的运输成本,每月降低的成本约为3 200元。
(4)同时新配送系统网络提高了库存的周转率,减少了装卸搬运次数,从而可降低装卸搬运费用,每月降低费用约为2 500元。另外减少装卸搬运次数,理论上也可降低白酒的破损率,提高安全度。
(5)从公司运营新配送系统网络的资金成本角度来看,库存的减少促使运输车辆、基础设施成本都有所减少,公司运营资本金减少,可提高资金效率和效益,从而减低总成本。
总之,优化后配送系统网络的成本比原网络总成本每月降低7.5%左右,但因为每一个要素的时间及空间数据的缺失或不完整,使得单一因素对总成本7.5%的影响只做了概算,且没有相互影响度的定量分析。
4 总结及建议
本文通过配送系统多设施选址的混合整数规划模型,以伊力特公司为研究对象研究该公司在新疆维吾尔自治区内的配送系统多设施选址。根据市场需求预测,在现有配送点的基础上进行模型构建、求解和实证。并把实证结果应用于实践,得出新的网络选址,在较好地满足市场的基础上,可降低配送总成本。
本文研究存在的不足之处:(1)因总厂、分厂和总库都在伊犁地区,所以把它们设为一个整体,没有具体划分。(2)对白酒没有详细分类,只考虑一种产品。(3)求解优化时并没有充分考虑网络运行的效率,仅以配送的最终费用为目标,因单一个要素数据不完整,没有进行要素间相互影响度的定量分析,只做了单一因素对总成本影响的概算。在后期的研究中进一步完善。

