岩溶区桥梁工程后注浆桩承载特性研究

文/宋劲松、王作丰、王晓鸣、李海涛

1 前言

后注浆技术为地下隐蔽工程，对后注浆桩基承载特性的研究，大部分还是通过现场试验以及模型试验等方法。刘彦峰[1]等通过现场静载试验得出桩侧注浆后，桩基承载和控制变形能力得到提升。钱建固等[2]基于大型接触面剪切试验建立了桩-土界面接触模型。随着计算机技术的发展，有限元分析成为桩基设计计算中的常用方法，黄吉龙等[3]采用数值模拟分析桩端后注浆桩的承载性能。本文将模拟桩侧后注浆桩的桩土位移及荷载沉降，并分析其承载性能。

2 有限元分析过程

2.1 模型的建立及模拟方案设计

为简化计算，对模型做出如下假定：

简化为轴对称模型；

桩周土以及注浆形成的注浆加固体为理想的弹塑性体，桩为理想弹性体；

后注浆只考虑浆液对土体的渗透。

桩定义为弹性材料，土体与注浆定义为理想弹塑性材料，本构模型采用莫尔-库伦模型。材料参数见表1。桩长L 为20m，桩径D 为1m。土体计算范围水平方向取10D，竖直方向取2L。

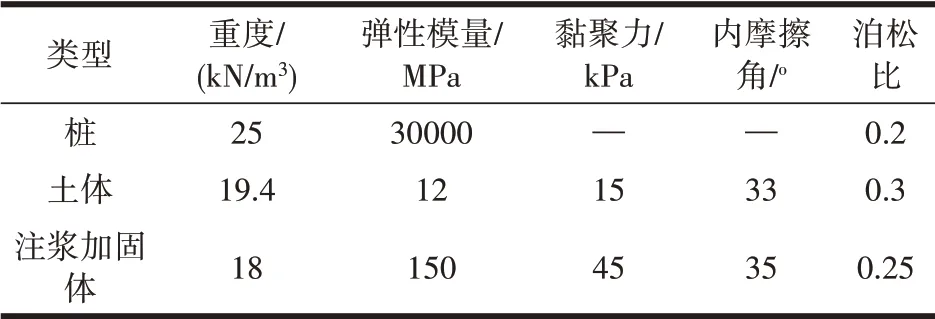
表1 数值模拟材料参数

2.2 接触定义

后注浆桩的有限元模拟涉及桩-土、桩-注浆加固体以及土-注浆加固体间的接触。有限元软件采用主-从接触算法，在桩-土界面、桩-注浆加固体界面中选择桩为主面，在土-注浆加固体界面中选择注浆加固体为主面[1]。

2.3 网格划分

在数值模拟分析中，网格划分的方式不同，其计算的进程以及结果的收敛性也不同。

未注浆桩和桩侧后注浆桩网格化完成后的模型如图1 所示。

图1 网格划分示意图

2.4 荷载和边界条件

对于二维轴对称模型，需要在其侧面限制水平位移以及在其底部限制两个方向的位移。本次计算将桩顶集中荷载换算为桩顶截面与之对应的均布荷载，并设置一系列的分级加载值[2]，见表2。

表2 荷载分级

3 数值模拟结果分析

3.1 注浆前后桩土位移场分析

以竖向荷载为5000kN 时为例，未注浆桩和桩侧后注浆桩在桩顶受竖向荷载作用时，桩土位移场分别如图2（a）和图2（b）所示，桩基通过注浆方式增强桩土间的相互作用，减小桩周土沉降，提高桩基承载能力。

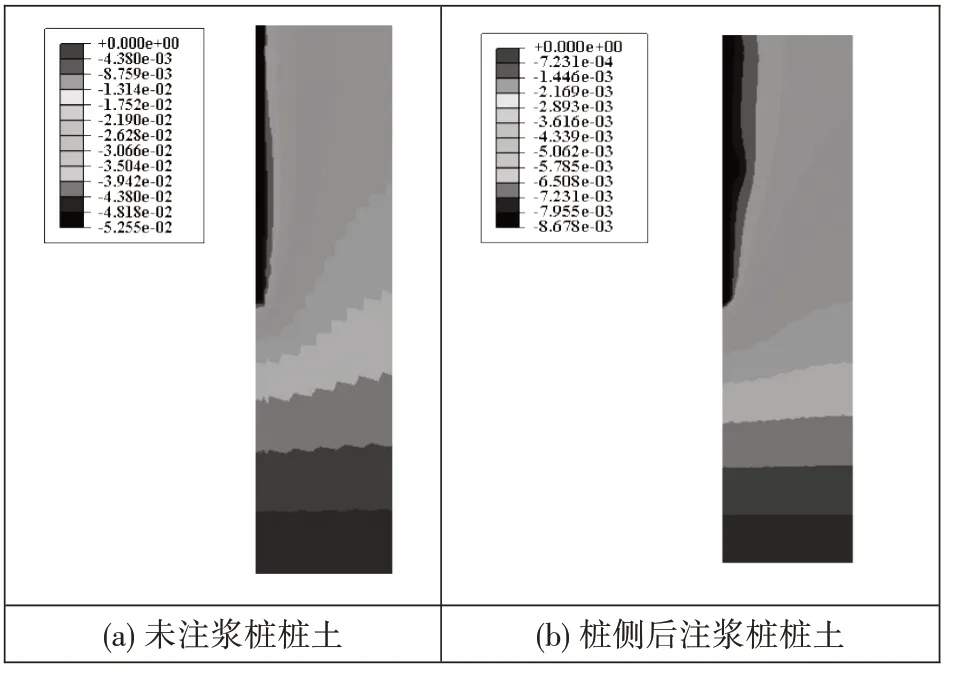
图2 位移云图

3.2 注浆前后单桩荷载-沉降关系分析

以竖向荷载为5000kN 时为例，未注浆桩和桩侧后注浆桩在桩顶受竖向荷载作用时，桩的受力变形特性如图3 所示。

图3 受力变形特性

未注浆桩和桩侧后注浆桩的荷载-沉降曲线如图4 和 图5 所 示。

图4 未注浆桩荷载-沉降曲线

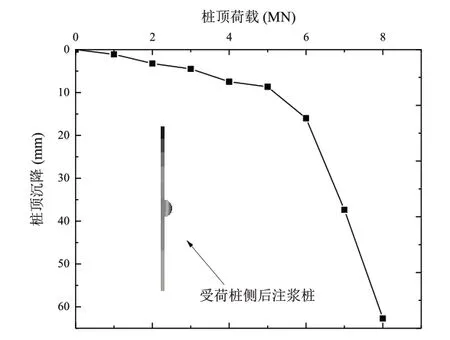
图5 桩侧后注浆桩荷载-沉降曲线

由图4 和图5 可知，相同荷载作用下，后注浆桩的沉降量均小于未注浆桩。未注浆桩荷载-沉降曲线的斜率要比注浆桩的斜率要大。未注浆桩的极限承载力为4000kN，桩侧后注浆桩的极限承载力为6000kN，即桩侧注浆后其极限承载力提升约为50%[3]。

3.3 不同注浆参数条件下后注浆桩单桩荷载-沉降关系分析

通过对不同注浆加固体尺寸的桩侧后注浆桩数值模拟，得到不同注浆参数条件下的后注浆桩的荷载-沉降关系曲线，如图6 所示。

图6 不同注浆参数下后注浆桩Q-s 曲线

由图6 可知，以桩顶荷载为6000kN 时为例，注浆加固体尺寸为rd=1.5m，h=5m，rc=1m 时，桩侧后注浆桩的桩顶沉降为16.016mm。而当注浆加固体尺寸增大为rd=2m，h=6m，rc=1.5m 时，桩侧后注浆桩的桩顶沉降为5.071mm。因此，当注浆加固体尺寸增大时，相同荷载作用下的桩顶沉降均明显减小。桩侧后注浆桩极限荷载的提升幅度与注浆加固体的尺寸成正相关关系。

4 结语

通过数值模拟研究未注浆桩和桩侧后注浆桩的桩土位移和荷载沉降，得出以下结论：

桩侧后注浆桩基相对未注浆桩基可以减小桩周土体沉降，提高桩基的承载能力。桩侧后注浆桩基相对未注浆桩基极限承载力提升约为50%。桩侧后注浆桩极限荷载的提升幅度与注浆加固体的尺寸成正相关关系。