龙卷风冲击高层建筑气动力效应数值模拟

俞怡恬，黄生洪，王 新

(中国科学技术大学工程科学学院，合肥 230026)

龙卷风是大气中强烈的涡旋现象，破坏力惊人，是风致灾害中比较严重的一种形式。过去，龙卷风主要发生在平原地区或城市郊区。由于地球环境变化，极端天气现象增多，城市环境也出现了较强的龙卷风天气。比较严重的如2016年发生在我国江苏盐城的EF4级龙卷风袭击事件，风力超过17级。2008年发生在美国亚特兰大市中心的龙卷风袭击，风速高达96 m/s，多栋摩天大楼被袭击。因此，针对高层建筑的龙卷风研究开始受到一定的重视[1-8]。

当前，现行的建筑设计规范还未给出与龙卷风相关的高层结构与安全设计要求，需要从理论、实验及模拟等多方面进行研究。由于龙卷风是一种强旋流动，与建筑结构相互作用时会诱导出复杂的涡系，基于雷诺平均NS方程(Reynolds-averaged Navier-Stokes equations, RANS)的模拟方法难以全面模拟这一复杂过程中的各种涡流现象。近年来，基于大涡模拟的研究逐渐展开，如Takeshi和Liu[9]在2014年通过应用大涡模拟数值研究了动态龙卷风的湍流对径向和垂直方向平均流场的影响。Liu和Takeshi[10]通过大涡模拟的方法研究了龙卷风的平移运动和粗糙度对类龙卷风旋涡的影响。Yao等[11]通过高分辨率的数值模拟，对处于华东地区的EF4级龙卷风的形成、结构和演变进行了研究。与此同时，相关实验室测量也在取得重要进展，早期如Sarkar等[2-3]通过平移龙卷风风场发生器测量了高层建筑模型的准稳态和瞬态风荷载效应，近来Maryam和Horia[12]采用1/11的龙卷风模拟模型，研究了类龙卷风旋涡以及流动对径向雷诺数的依赖关系。Alireza和Partha[13]在实验室条件下模拟了龙卷风对低层建筑的作用，影响因素包括涡流比、平移速度以及建筑模型参数。Cao等[14-15]建立了小型龙卷风模拟实验平台，研究了龙卷风对冷却塔等结构的荷载特征。综合来看，由于实验室模拟的龙卷风尺度有限，高层建筑在实验室模拟的龙卷风尺度下需要较大的缩尺比。不合适的缩比关系可能带来存在一定的尺度效应，使得相关气动载荷呈现一定差异。目前这方面的相关研究还鲜见详细报道。

本文在前期研究的基础上[16]针对Sarkar等[3]开展的龙卷风冲击高层建筑模型实验进一步展开大涡模拟(LES)研究，研究了实验条件下龙卷风旋涡绕过建筑模型的流场演化及气动载荷特性，并与文献[17]提供的实验测量结果进行了比较验证，进而针对全尺寸龙卷风冲击不同尺度和形状的高层建筑流场展开了深入研究。

1 数值模型及验证

本文采用的龙卷风数值风场模型是基于Wen[18]提出的三维龙卷风风场模型。为使龙卷风在水平方向发生移动，则需在此基础上叠加水平移动速度。此模型的有效性已在王新等[16]的文章中实现并开展了基于RANS模拟的校核，本文将在大涡模拟条件下进一步应用和校核。

已有的运动龙卷风模拟方法多数采用直接模拟龙卷风发生装置结构，这往往需要用到运动网格或滑移网格，不仅计算复杂，且计算效率较低。本文模拟实际龙卷风运动设计了如图1(b)所示的计算模型，通过在计算域顶部设定一个按理论模型风速运动的驱动区驱动龙卷风运动。在龙卷风平移且未与建筑作用之前(地表条件一定)，可使自身涡量、形状及速度大小保持稳定，这样有利于准确计算和比较不同条件的龙卷风作用建筑时的风荷载。驱动区风速模型如式(1)所示。

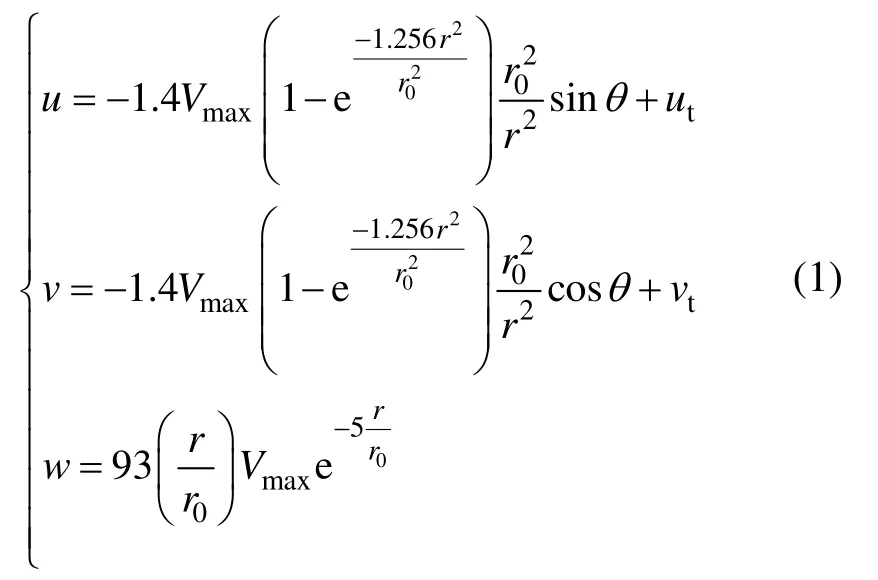
式中：u、v、w分别为沿x轴、y轴、z轴的速度分量；θ为位置矢量在xoy平面上的投影r与y轴的夹角；Vmax为龙卷风旋转时最大切向速度；r0为最大切向风速半径；ut、vt分别为龙卷风在xy平面内平移时的平移速度分量。

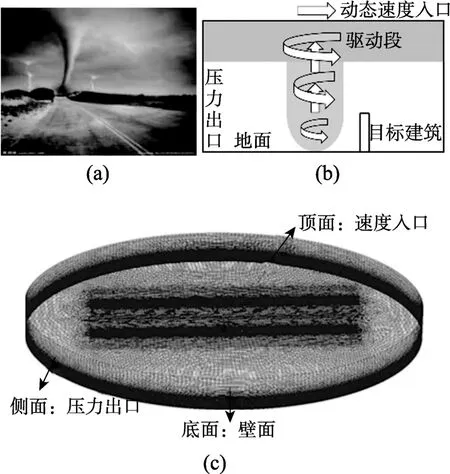
图1 龙卷风数值模型示意图Fig.1 Diagam of tornado numerical model

计算域为如图1所示的圆柱型区域，尺寸为直径×高=30 m×1.2 m；建筑模型尺寸与实验模型[3]的尺寸相同，为长×宽×高=0.108 m×0.108 m×0.432 m。网格划分小尺度为0.0005 m，网格总量共计830.64 万；龙卷风特征参数与参考文献[2-3]实验测得的特征参数相同，即沿y轴方向的最大风速与实验室中最大切向风速相对应，为Vmax=11 m/s，当龙卷风水平移动速度为0.3 m/s时，与Vmax相对应的龙卷风涡核半径r0=0.36 m。

模拟采用Fluent大涡模拟模块进行，驱动段采用User Defined Functions(UDF)函数实现。求解器为三维、基于压力耦合的非定常求解器；大涡模拟模型采用一方程动能输运动力模式；采用二阶隐式的时间离散格式以及二阶中心差分空间离散格式。为了证明本文所采用计算方法的可靠性，首先将应用本文方法模拟获得的龙卷风速度分布特征与文献[17]提供的实验结果进行对比；

图2所示为龙卷风在以不同速度平移的过程中，不同时刻、不同高度的速度分布特征与文献[18]给出的实验测量结果的对比。可以看出，数值计算结果与实验结果整体上具有很好的一致性。图3所示为模拟的龙卷风以0.3 m/s及0.6 m/s的速度沿x轴方向水平运动过程中在不同时刻的涡量等值面图(等值面上颜色代表速度高低)；可见，虽然涡量随着时间不断变化，但总体来看，龙卷风的涡流形状和速度大小在移动过程中都具有良好的自保持性，说明文中采用的龙卷风数值模型在大涡模拟计算的平移过程中具有不错的稳定性。综上所述，本文所采用龙卷风模型和大涡模拟数值算法可以准确地模拟龙卷风平移过程中的基本风场特征。

图4进一步比较了所模拟的龙卷风动态冲击目标建筑模型的过程中，本文计算获得的x-y平面内的气动载荷系数与文献[18]所提供实验值的对比，x-y平面内的载荷系数分别由式(2)和式(3)确定：

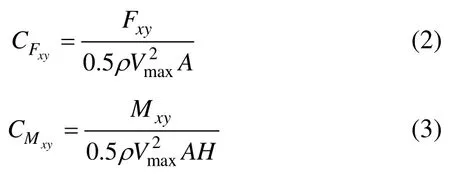
式中：Fxy为xy平面内的升力和阻力的合力；Mxy为扭矩；ρ为密度；A为建筑模型水平截面的面积；H为建筑模型的高度。同时对照给出了基于雷诺时平均模型(Reynolds time-averaged Navior Stokes equations，RANS)计算结果。可见RANS模型模拟获得的气动力载荷较为光滑，其峰值与实验结果(HS对应0.6 m/s平移工况，LS对应0.3 m/s平移工况，QS对应准静态工况)略有差异(特别是前峰值低于实验值)，而大涡模拟结果与实验值无论峰值和脉动均与实验值接近，只是横轴对应荷载相位与实验值略有差异。这可能与实验龙卷风发生器平移运动(强迫平移)与数值模拟的平移运动速度(由驱动段诱导按一定速率平移)的差异有关。上述结果证明，采用的大涡模拟数值模拟方法和模型可以较准确地模拟龙卷风的动态涡流动。

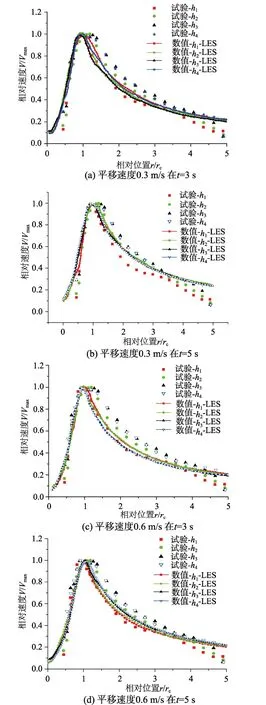
图2 龙卷风在不同平移速度下，速度分布的数值结果与实验结果[18]的对比Fig.2 Comparison of velocity profiles between numerical results and measured values in the translation moving of tornado

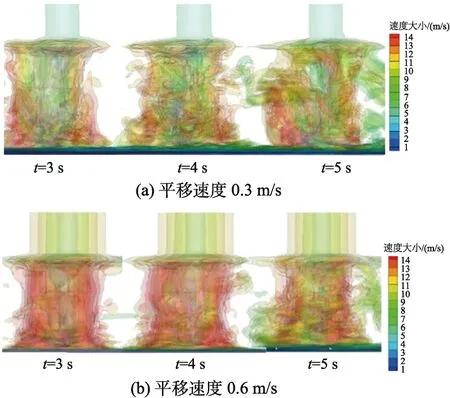
图3 速度标示的涡量等值面云图Fig.3 Iso-surfaces of vorticity colored by velocity magnitudes

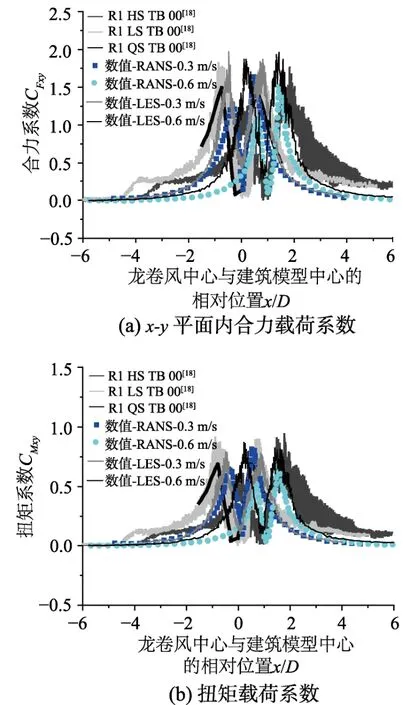
图4 x-y平面载荷系数响应Fig.4 Load coefficients comparison in xy plane

2 主要结果及讨论

在前述校核基础上，进一步开展了全尺寸龙卷风冲击不同形状和尺度建筑结构的大涡模拟，设计了以下几种高层建筑模型，尺寸分别为：1) 以文献[3]实验尺度下建筑模型相对龙卷风半径的比例等比例放大，使其高度达到216 m：模型SQ1具体尺寸为长×宽×高=17 m×17 m×216 m；2) 文献[3]实验用建筑模型(1∶200)的原型：模型SQ2具体尺寸为长×宽×高=54 m×54 m×216 m；3) 圆形建筑模型，截面面积与全尺寸模型2相等：模型Circle具体尺寸为底面直径×高=30 m×216 m；4) CAARC标准建筑模型具体尺寸为长×宽×高=30.48 m×45.72 m×182.88 m，对于该建筑模型，再分为0°攻角和90°攻角两种模型进行气动载荷响应特性的研究，沿龙卷风平移方向，0°攻角为长30.48 m的一面作为迎风面，90°攻角为长45.72 m的一面作为迎风面。具体如图5所示。

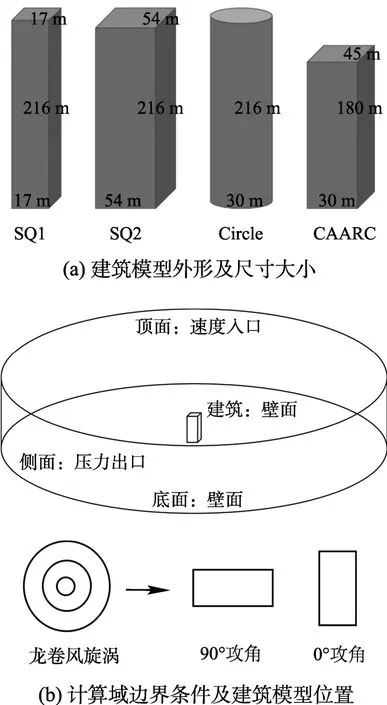
图5 全尺寸目标建筑及计算域模型Fig.5 Target buildings and computation domain for full scale cases

计算域扩大为直径4000 m，高度500 m的圆柱区域，建筑置于计算域中央，在x-y平面的坐标为(0，0)；受计算资源的限制，经反复权衡，最小网格尺寸为0.5 m×0.5 m×0.8 m，在龙卷风的主要影响区域，网格相对其他区域有所加密，网格总量达到了1200.3万。图5(b)所示为计算模型的边界条件设置和建筑模型在计算域中的相对位置。F2级龙卷风的初始位置在xy平面中的坐标为(-600 m，0)，以F2级龙卷风的实际水平移动速度V=12.6 m/s沿x轴正向移动，时间步长设为0.005 s。运动总时间设置为100 s，按平移速度，龙卷风将运动到建筑的另一侧600 m位置。采用与前述数值校核相同的大涡模拟算法和模型。F2级龙卷风的基本参数如表1所示。

表1 F2级龙卷风基本参数Table 1 Basic parameters of F2 tornado

图6(a)和图6(b)所示为实验室尺寸下和全尺寸下龙卷风对建筑模型气动载荷响应特性，其中，两组算例中建筑模型相对龙卷风的尺寸基本相同，实验模型为B/D=0.15，SQ1为B/D=0.17。通过比较，发现两组气动载荷响应曲线都具有相同的趋势，都呈现双峰值的现象。但差异也较为明显，首先是峰值出现的相对位置，合力系数曲线和扭矩系数曲线的峰值都是全尺寸下的前峰值迟于实验尺寸下的前峰值，后峰值则早于实验尺寸工况。其次是峰值的大小，在合力系数曲线中，实验尺度的载荷响应峰值是前峰明显小于后峰，而全尺寸下的载荷响应峰值则是后峰值略小于前峰值；扭矩系数曲线中虽然两组算例的峰值都是前后峰值一致，但是实验尺度下的载荷峰值明显小于全尺寸下的载荷峰值。以上说明龙卷风对建筑的冲击作用的确存在一定的尺度效应，实验室尺度峰值预测结果显然偏低于全尺度，且载荷变化斜率也偏低。这可能部分体现了尺度和风速不同带来的雷诺数效应。具体来看，与实验室尺度模拟来比，全尺度模拟龙卷风工况的雷诺数要高近三个数量级(105∶108)。根据最新文献[19]实验研究结果(最高雷诺数1×107)，钝体建筑在雷诺数1×106附近存在一个阻力减小的区域，但在雷诺数5×106后逐渐恢复。在更高的雷诺数区域内尽管没有实验结果，但普遍认为阻力、升力系数会有所升高。本文模拟条件下，显然错过了阻力减小区域，因此全尺度模拟结果显示的峰值水平力系数略高于实验尺度下的值应该是合理的。同时也说明，风洞尺度下，受雷诺数效应影响，应避免将实验雷诺数选取在阻力危机区，这样获得的结果不会带来较大的偏差(除非专门研究)。

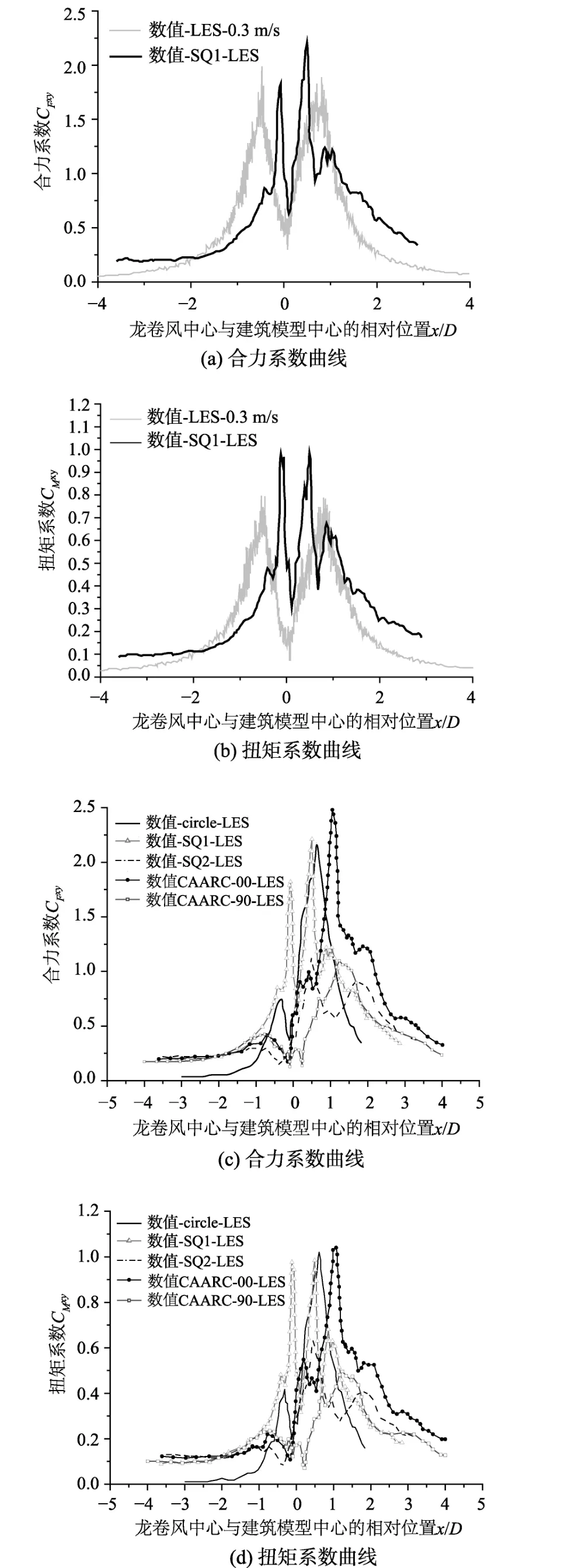
图6 各工况载荷系数曲线Fig.6 Load coefficients curves for all cases

另外比较可见：实验室尺度模拟结果和实验结果均展现了较丰富的脉动特征，而全尺度大涡模拟结果呈现的脉动特征较少，这主要是因为缩尺模拟下网格密度高，分辨出来的涡系较多，多数较小尺度的涡与缩比的建筑模型尺度比较起来差别不大，因此存在较强的耦合作用，风荷载呈现大量的高频脉动特征。全尺度模拟下，受计算资源的限制，网格相对较稀疏，大涡模拟能分辨的涡系较少，尺度偏大，很多小尺度涡未分辨出来，而全尺寸建筑尺度偏大，因此载荷的高频脉动量偏少。另外，即使在真实情况下，根据湍流理论，一定湍流度下，小尺度涡尽管能量小，但数量较多。实验条件下采用缩比模型，由于缩比尺度大，缩比后的模型尺度小，对其有影响的涡自然偏多，耦合作用下其高频载荷脉动自然偏多。而全尺度下，建筑尺度偏大，对其有影响的涡自然偏少，其高频脉动载荷自然偏少。所以从这个角度说，这也是尺度效应的一种表现。

图6(c)和图6(d)所示为全尺寸下龙卷风冲击其他形状和尺寸建筑的气动载荷响应特性曲线。通过比较可以发现，建筑形状和特征相对尺寸，如B/D(建筑模型水平截面特征尺度/龙卷风特征直径)对气动荷载结果影响较大。建筑模型的B/D值较大时的载荷峰值的大小明显小于B/D值偏小时的载荷峰值，表现最明显的就是SQ1和SQ2之间的对比；且在不同形状和尺寸下，其峰值数量和位置也存在较大的区别。

通过对图7各工况的载荷响应典型位置时刻水平剖面速度流线图的分析。可以对不同形状和尺寸下的具体载荷响应特性作进一步的分析。对于建筑模型SQ1，即建筑模型水平截面特征尺寸与龙卷风特征半径尺寸相差较大时，从图7(a)可以看出，此时龙卷风旋涡内部分裂出两个明显的小旋涡直接撞击建筑模型的前后壁面，形成明显的双峰值载荷现象。当建筑模型水平截面尺寸与龙卷风特征尺寸相近时，如图7(b)所示的SQ2，龙卷风旋涡分裂成两个旋涡后从建筑的一侧绕过，使整体的载荷系数值小于建筑模型SQ1，且双峰值现象也没建筑模型SQ1明显。图7(c)和图7(d)是同一标准建筑模型CAARC在龙卷风不同角度攻击下的水平剖面流场结果，可以发现，两者的旋涡绕过方式具有相似性，都在接近建筑物时开始分裂出多个小旋涡，在绕过建筑模型后各小旋涡间相互作用，形成尾流效应，使得载荷系数的最大值发生在旋涡中心离开建筑之后。并且，由于0°攻角时的迎风面积更大，其载荷峰值要稍大于90°攻角时的载荷峰值。图7(e)所示为圆形截面建筑模型的计算结果，可以发现其龙卷风旋涡作用方式与上述几个算例具有较大的差别。龙卷风旋涡在整个变化过程中保持完整的单旋涡状态，对应图6(c)和图6(d)中明显的峰值表现。

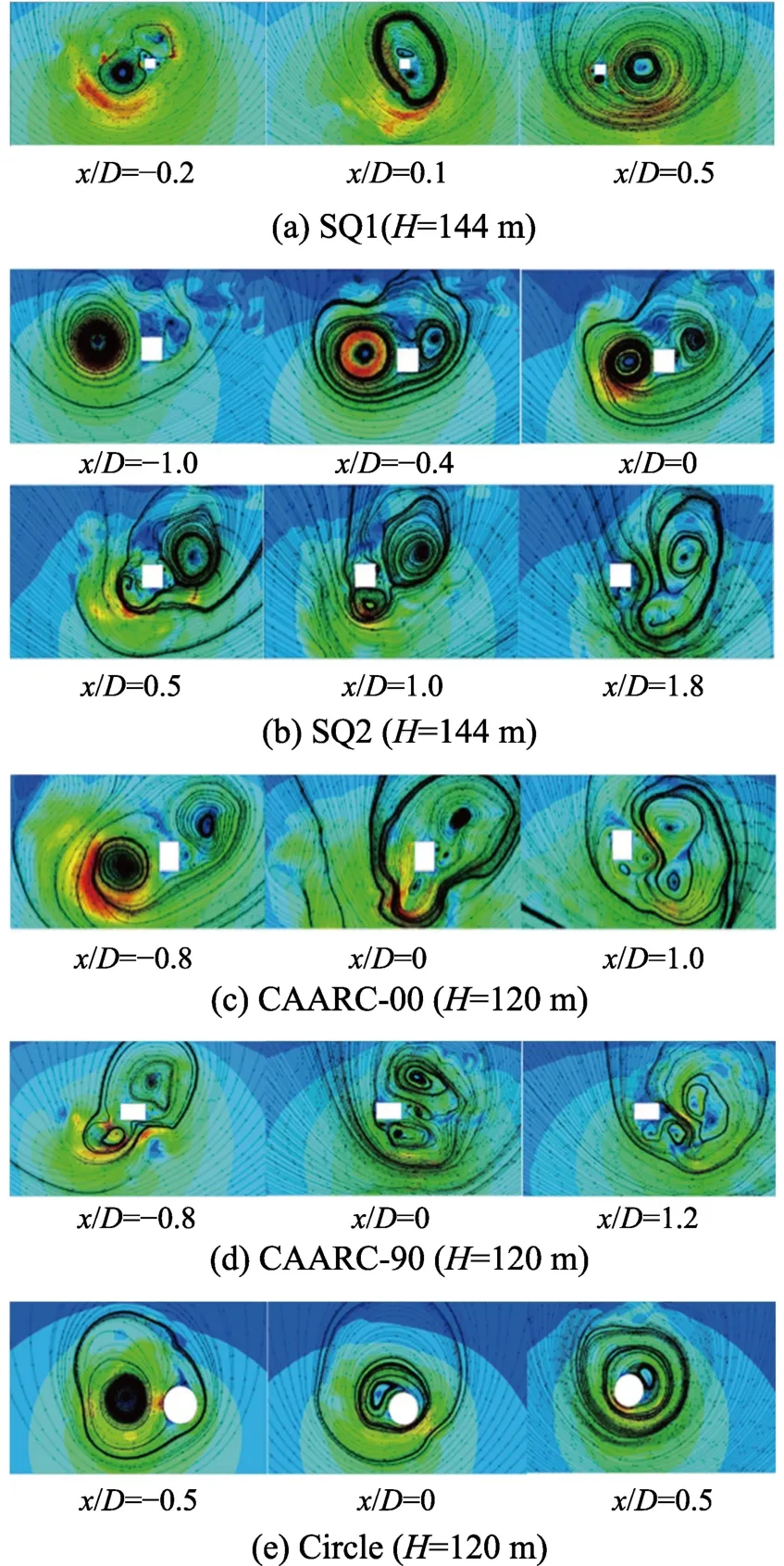
图7 各工况水平剖面速度流线图Fig.7 Velocity contours and stream lines on a typical horizontal plane for different cases

3 结论

(1) 实验室尺度下的数值校核表明，本文采用的大涡模拟运动龙卷风数值模型和算法可较准确刻画龙卷风的平移稳定性，基本风场特征，预测冲击高层建筑的复杂流场和气动载荷。但全尺度下，受网格量的限制，对高频脉动载荷的预测偏低。

(2) 实验室尺度下模拟的龙卷风对建筑的冲击作用存在一定的尺度效应，其峰值预测结果偏低于全尺度工况，且载荷时变特性也偏低。不过，雷诺数效应分析表明，龙卷风风洞尺度下将实验雷诺数选取在阻力危机区外，不会带来较大的偏差。

(3) 全尺寸条件下，龙卷风对建筑模型的冲击作用，与建筑模型的形状、尺寸以及攻角都均有相关性，其中建筑模型水平截面特征尺度与龙卷风特征直径比为控制参数之一。不同的值范围对应龙卷风冲击时的漩涡演化存在差异，同时对应其载荷变化特征。而对不同截面形状来说，长方形截面建筑的龙卷风气动载荷响应系数值相对较大，且与龙卷风冲击过程中的攻角有关。

需要说明的是：本文在校核了基于实验室尺度的模型后开展了全尺度的大涡模拟。受计算资源限制，全尺度大涡模拟网格量有限，可能平均了一些较小涡，导致荷载结果中高频脉动偏少。后续工作中将开展更精细的计算研究，揭示龙卷风作用下更复杂的载荷机理。