基于Hoek-Brown准则的岩体弹塑性损伤模型及其应力回映算法研究

许梦飞，姜谙男，史洪涛，李兴盛

(1.大连海事大学道路与桥梁工程研究所，辽宁，大连 116026；2.中铁建大桥工程局集团第一工程有限公司，辽宁，大连 116026；3.中铁一局集团第二工程有限公司，河北，唐山063000)

在岩体工程开挖过程中，岩体介质内部随着裂隙的发育，贯通产生损伤，导致其强度和刚度发生劣化，并伴随有塑性流动变形。相当部分岩体的力学行为不但受岩体结构、岩块强度、应力状态等因素影响，并且具有强度非线性和应变软化特征。同时地下水在岩体内部将产生孔隙水压力，会影响岩体的力学性质和破坏模式。因此，为了更好地反映岩体的力学行为规律，建立合理的岩体弹塑性损伤本构模型具有重要的意义。

近年来，国内外学者根据弹塑性力学、连续损伤力学理论对岩石弹塑性损伤模型进行了研究，包括引入合理的屈服函数、损伤变量演化方程和建立稳健的数值求解算法。Luccioni和Armero等[1-2]基于热力学框架阐述了塑性与损伤的耦合机理，并给出了耦合模型的数值积分算法。Shao、Salari、王军祥和袁小平等[3-6]建立了基于Druker-Prager (DP)的岩石弹塑性损伤模型，较好地反映了损伤对粘聚力和刚度的弱化作用。王永亮等[7-8]推导了DP准则下非均匀岩石损伤本构模型，并与流固耦合理论相结合，开发了损伤岩石的渗流求解程序。刘杨等[9]建立了基于Mohr-Coulomb(MC)准则的弹塑性损伤本构模型，并推导了模型在主应力空间中的应力回映算法，解决了MC准则在数值计算中的奇异点问题。贾善坡等[10]针对泥岩的力学试验特性，以等效塑性应变为损伤内变量，建立了基于MC准则的塑性损伤模型和蠕变损伤模型，并在ABAQUS平台上实现了模型的数值求解。杨强等[11]利用细观力学方法建立了岩土材料的弹塑性损伤模型，该模型能够模拟岩土破坏中的局部化问题。杜修力等[12]结合非线性统一强度模型和考虑围压作用的损伤演化方程建立了一种岩石三维弹塑性损伤模型。

已有岩石弹塑性损伤模型大多采用MC或DP等线性强度准则。同DP和MC准则相比，广义Hoek-Brown(HB)屈服准则[13]更能够反映岩体的非线性特征及结构面、开挖扰动等因素对岩体强度的影响，因此被广泛应用于岩体工程稳定性评价当中。朱合华等[14]阐述了HB强度准则的研究进展，并提出一种广义三维HB强度准则。吴顺顺等[15]研究了HB准则下的隧道纵向变形曲线。刘立鹏、宗全兵等[16-17]分析了HB参数对边坡稳定性的影响。孙闯等[18]提出了简化HB应变软化模型，并在此模型基础上，采用收敛-约束法对隧道支护结构的稳定性进行分析。

由于HB准则在棱线和尖点处存在不连续性，导致其有限元数值求解过程十分困难。对此，Hoek、Sofianos和Priest等[19-21]提出了HB准则参数与MC准则参数的等价方法。Pan、Wan和Merifield等[22-24]通过将HB准则的角点进行圆滑处理或修改屈服函数的方法，避免了数值求解中的奇异点问题。然而，等价参数法存在一定的使用范围(应力值在最大围压值与抗拉强度之间)，角点圆滑法本质上修改了屈服函数形式，使其在求解一些经典问题时(地基承载力、边坡安全系数)会产生偏差。Clausen、陈陪帅等[25-26]建立了主应力空间中HB准则的完全隐式应力回映算法，该方法在处理奇异点问题时具有一定的优势，是当前本构积分算法的研究热点。

数值积分的困难限制了HB模型在有限元数值模拟中的应用，基于HB模型的损伤本构研究则更为少见。为了更好地反映岩体介质的损伤演化特性，本文引入修正有效应力原理，考虑孔隙水压力作用，建立了基于HB准则的弹塑性损伤耦合模型，从损伤和塑性两个方面反映岩石材料的劣化机制；推导了主应力空间弹塑性损伤本构方程的完全隐式返回映射求解算法；基于ABAQUS的用户子程序接口Umat，建立三维数值程序；最后，通过室内单轴、三轴压缩试验和工程案例对模型进行了验证和应用。

1 基于HB准则的弹塑性损伤模型

1.1 考虑损伤的HB弹塑性本构模型

基于HB模型的弹塑性损伤屈服函数和塑性势函数表达式分别为：

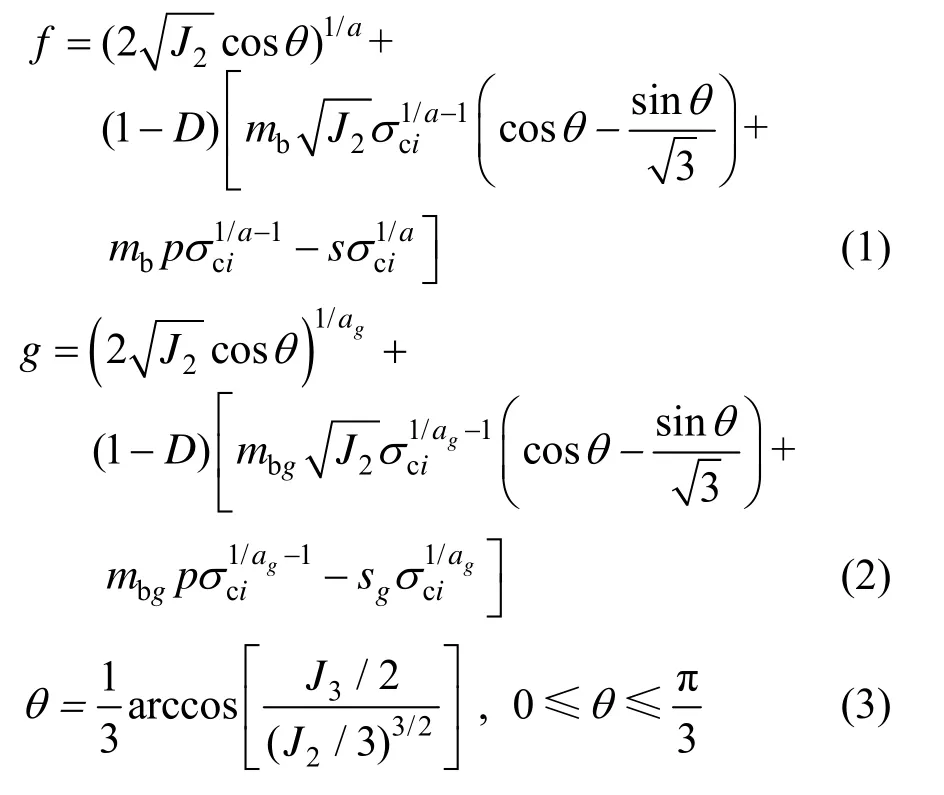
式中：p为静水压力；J2、J3分别为第二、第三偏应力不变量；θ为罗德角；mb、s、σci和a为HB准则参数，mbg、sg、ag为对应的塑性势函数参数；D为损伤变量。参考已有研究，岩体损伤对HB参数的影响主要体现在对mb和s[27]的弱化作用。因此本文假定损伤只对参数mb、s产生影响，受荷过程中σci和a保持不变。

针对3个主应力之间的大小关系，式(1)在主应力空间中可以写成多个屈服函数的形式：

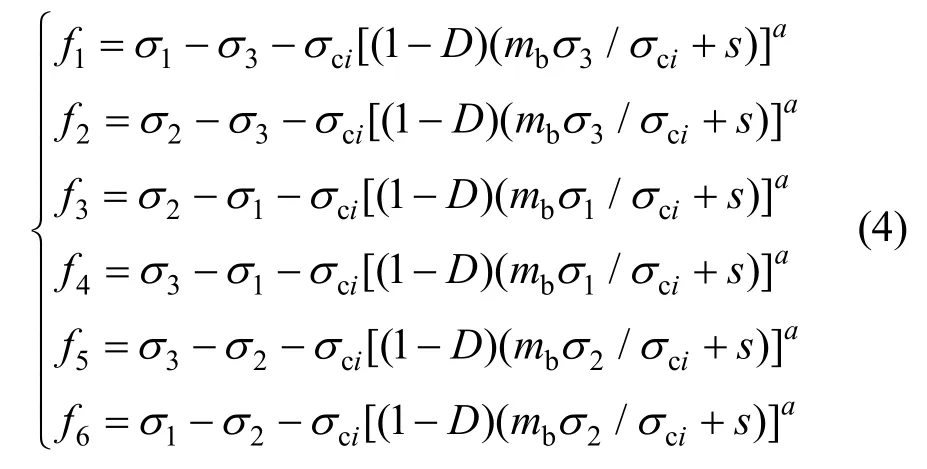
塑性势函数gi与对应的屈服函数形式相同，由参数mbg、sg、ag分别替换mb、s、a即可，图1为H-B准则在主应力空间中的图形。

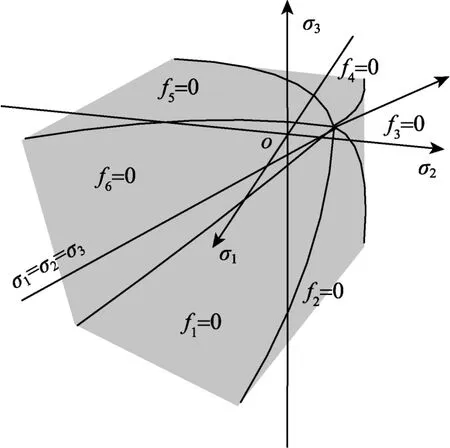
图1 HB准则在主应力空间的图形Fig.1 HB criterion in principal stress space

多屈服面本构模型的流动法则表达式为：

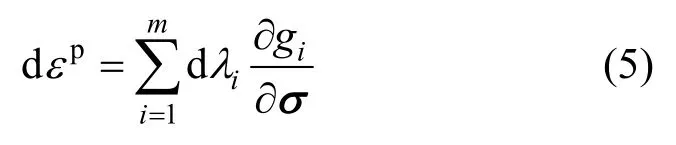
式中：dεp为塑性应变增量；dλi为塑性因子增量；m为式(4)中大于零的屈服函数的个数。

硬化规律由式(6)进行控制：

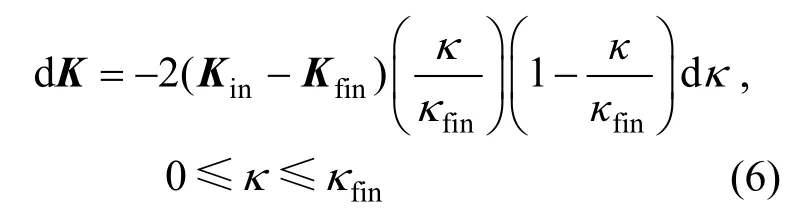
式中：K为硬化参数向量，K=｛mb,s｝ ;Kin为mb、s的初始强度；Kfin为mb、s的残余强度；当Kin＞Kfin时，材料发生软化，Kin＜Kfin时，材料发生硬化，Kin=Kfin时，材料为理想弹塑性[28]；κ为塑性内变量，本文取κ=γp，γp为塑性剪切应变，dγp=dε1-dε3；κfin为岩石发生破坏时的塑性内变量。

由Kuhn-Tucker加卸载准则可得：

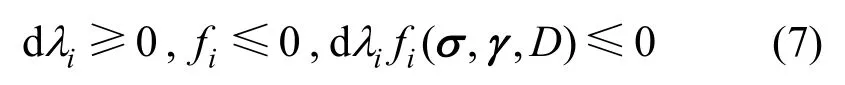
考虑损伤的应力-应变本构关系为：

式中：εe为弹性应变张量；为损伤弹性矩阵，为四阶对称张量，分别为损伤剪切模量和体积模量。

G(D)、K(D)可以用初始剪切模量G0和初始体积模量K0表示：

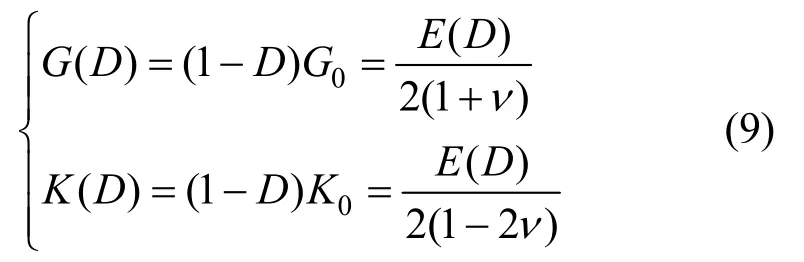
由式(9)可知，损伤最终导致了弹性模量的弱化。如图2所示，当应变达到一定的阈值时，弹性模量值随着损伤的累积开始减小，材料应力-应变关系显现出非线性特征。

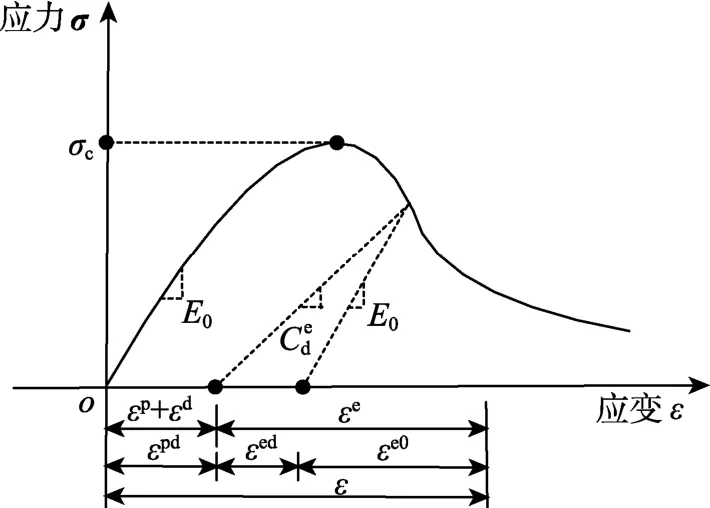
图2 损伤引起刚度退化Fig.2 Stiffness degeneration caused by damage

1.2 损伤变量D的演化方程

本文将损伤变量D表示为等效塑性应变的幂指数函数形式：

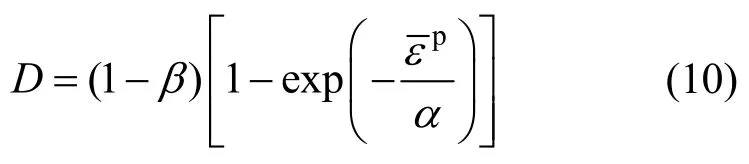
式中：α取值范围为[0, +∞]，决定了损伤后岩石材料软化曲线的初始斜率；β取值范围为[0,1]，决定了岩石最大损伤值。不同α、β值下的损伤变量变化曲线如图3所示。从图3可以看出：α越大，损伤演化速率越慢；β越大，岩石的最终损伤值越小。

为等效塑性应变，其表达式为：

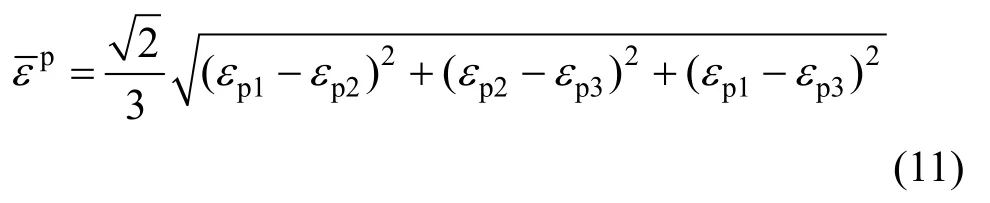
式中，εp1、εp2、εp3分别为三个方向的主塑性应变。

图3 损伤参数对损伤演化规律的影响Fig.3 The influence of damage parameters on damage evolution

1.3 修正有效应力公式

岩体是由岩石骨架和相互连通的孔隙以及其中储存的流体组成的多孔介质，在流体运动作用下，岩石力学性质会发生改变。根据Biot理论，岩体有效应力表达式为：

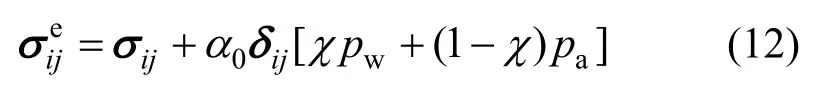
式中：为有效应力；σ为总应力；δ为ijijKronecker符号；α0为Biot系数，通常取α=1；pw和pa分别为孔隙水压力和孔隙气压力；χ与饱和度和表面张力有关，一般取χ=sw，sw为孔隙水饱和度。

2 弹塑性损伤模型数值积分算法

式(1)不变量的形式在塑性计算中经常使用，但其形式较为复杂[9]，且HB模型存在棱线和尖点处的奇异点，在这些奇异点处屈服函数外法线方向不唯一，导数不连续，使得数值实施存在一定的困难。因此本文从主应力空间角度出发，对HB弹塑性损伤模型完全隐式的返回映射求解算法进行推导：在塑性状态求解过程中，首先对应力空间进行划分，判断应力回映点的位置(单一屈服面、双屈服面相交的棱线或者多屈服面相交的尖点处)，根据回映位置的不同，建立更新应力及多个或单一塑性因子的Newton-Raphson求解式，很好地解决了空间角点问题。通过ABAQUS软件的用户子程序接口Umat，实现考虑孔隙水压作用的弹塑性损伤模型三维数值求解过程。HB弹塑性损伤模型返回映射求解算法分为弹性预测、塑性修正和损伤修正三个部分，其中，弹性预测与塑性修正均在有效应力空间进行，最后通过损伤修正得到最终的名义应力。具体求解步骤如下。

2.1 主应力空间应力回映算法

步骤1.弹性预测

已知tn时刻应变增量Δεn+1、应力σn、硬化内变量κn和损伤变量Dn，则tn+1时刻的弹性预测应力为：

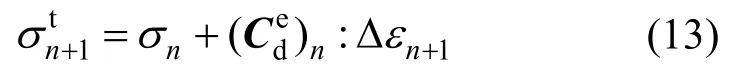
若f1＜0，材料仍处于弹性阶段，对变量进行更新：

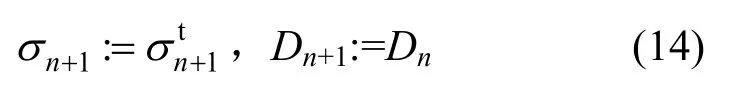
若f1＞0，则进入塑性修正阶段。

步骤2.塑性修正

塑性修正过程中，保持应变增量Δεn+1及损伤变量Dn不变，塑性状态下应变增量中包含弹性应变增量Δεe和塑性应变增量Δεp，塑性应变增量表达式为：

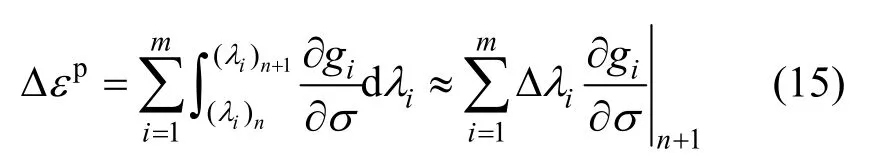
式中：m为式(4)中函数值大于零的方程个数；n+1指的是tn+1时刻。基于返回应力的位置，式(15)具有不同的形式，当返回应力位于屈服面、棱线或尖点处时，分别需要求解1个、2个或3个塑性因子。

此时的更新应力位于屈服面以外，需要对其进行修正，修正量Δσp的表达式为：

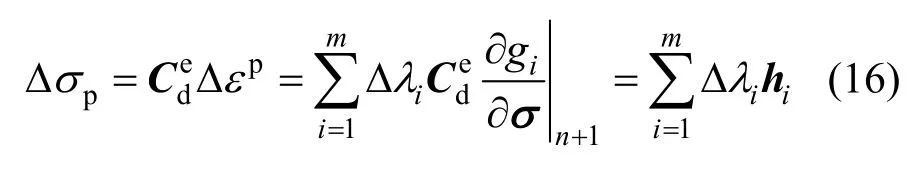
更新后的应力和内变量表达式为：

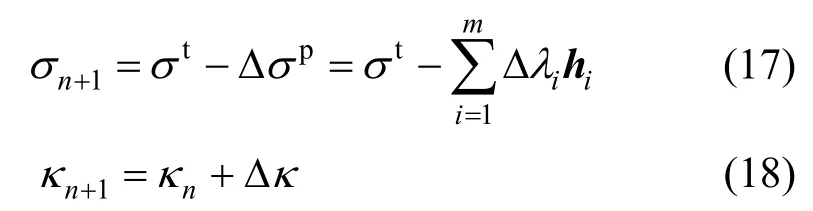
1) 应力返回位置的判断

在f1与f2的交线l1上有σ1=σ2(为方便描述，对下标n进行省略)，因此直线方程为：

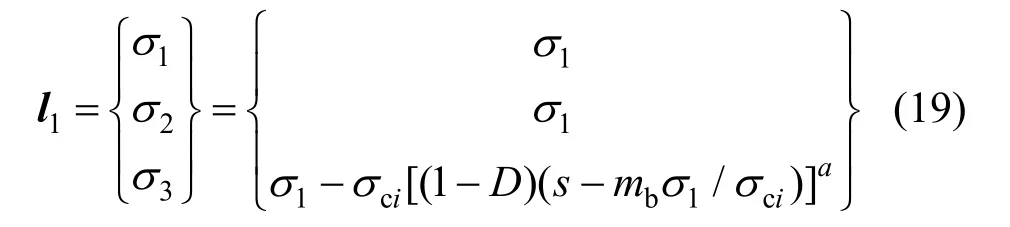
同理，f1和f6的交线l6上有σ2=σ3，直线方程为：

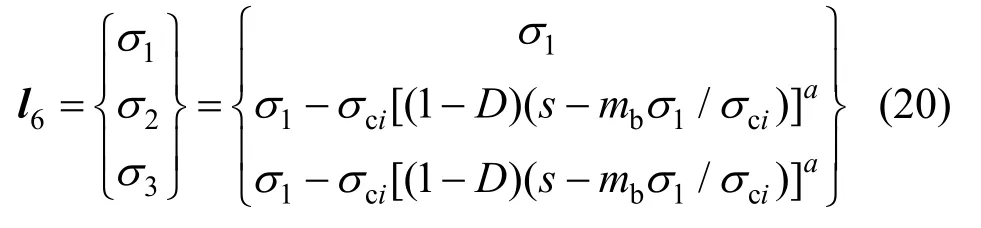
当更新应力只位于屈服面f1上时，由式(16)可得此时塑性修正应力增量的方向h1：

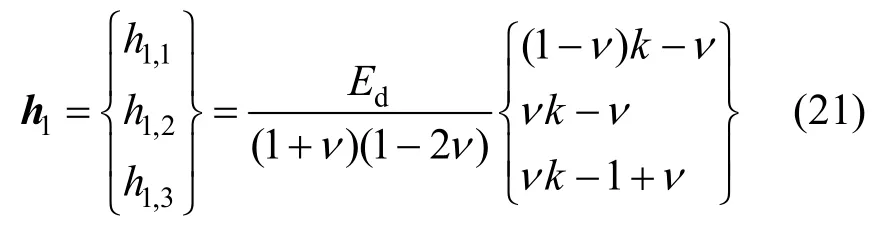
式中：ν为泊松比；k的表达式如下：

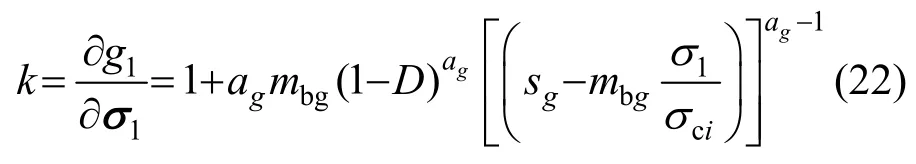
图4对应力空间进行了区域划分。由图4可以看出，h1与f1的两条边界线组成的边界面确定了应返回至f1面的应力区域；h1、h2和f1、f2的交线确定了返回至l1线的区域，h1、h6和f1、f2的交线确定了返回值l6线的区域。

在l1上取一点σl1=(σ1,σ1,σ3,),l6上取一点σl6=(σ1,σ3,σ3)，若同时满足：

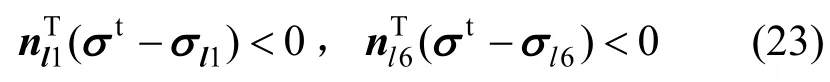
则更新应力位于f1面上。式中：

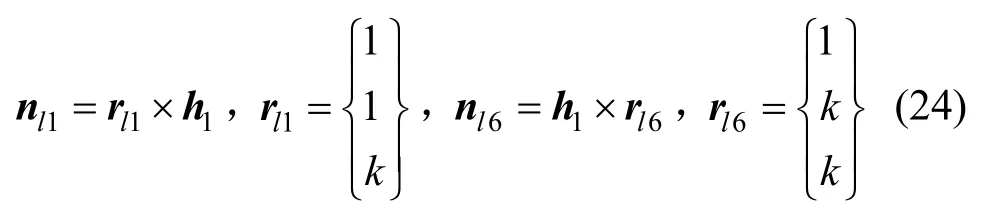
式中，rl1、rl6为棱线l1和l6的方向向量。

由图4可以看到，由h1、h2组成的平面将尖点位置与l1分割开来，该平面的法向量为：

由h1、h6组成的平面将尖点位置与l6区域分割开来，平面法向量为：

尖点处应力值为σapex=(σa,σa,σa)，σa=sσci/mb。若有：同时成立，则更新应力位于尖点处。

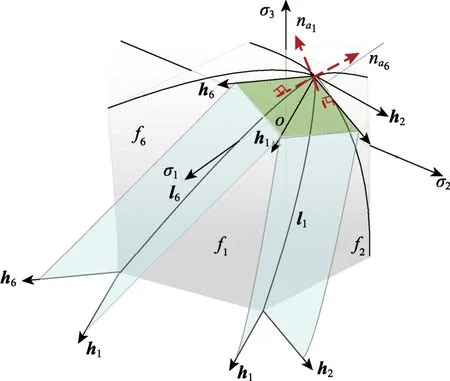
图4 HB准则在主应力空间的区域划分Fig.4 Regional division for HB criterion in principal stress space

2) 应力及内变量求解

应力求解过程的关键是对方程组式(27)进行求解，即：

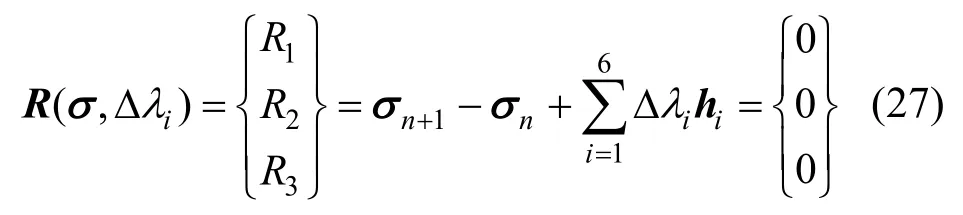
式中，R为残差值。

当应力回映到f1上时，式(27)可以写为:

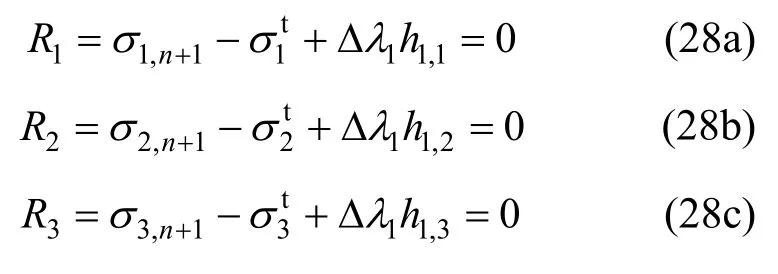
求解时首先对式(28a)进行求解，建立关于σ1,n+1和Δλ1的Newton-Raphson式：

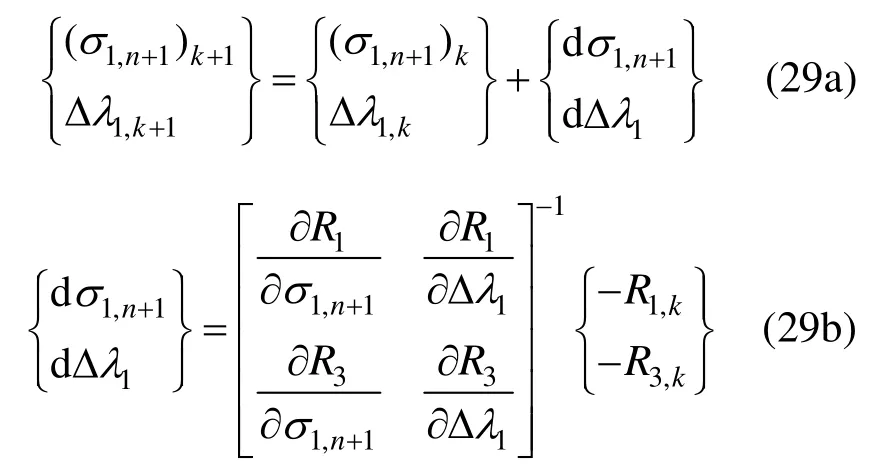
式中，k为迭代步数。

为确保Δλ1非负，应按照下式进行更新：

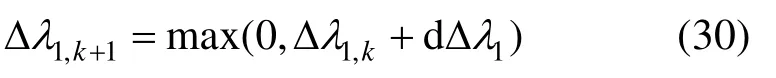
求解出σ1,n+1和Δλ1后，代入f1=0中求解σ3,n+1，最后由式(28b)求出σ2,n+1。求解完成后，对γp进行更新，由式(6)获取更新硬化参数K。

当应力回映至l1上，满足σ1=σ2，式(27)可以写为：

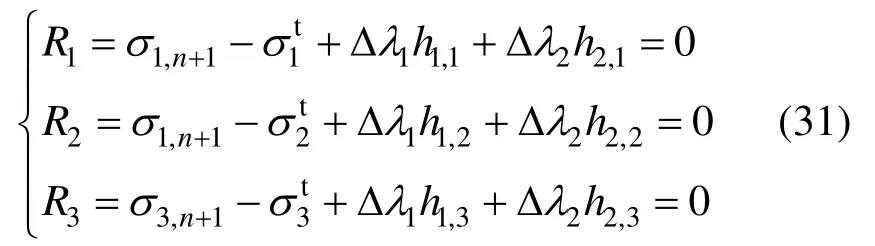
式中：

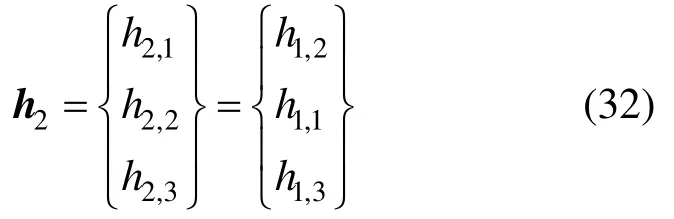
此时，式(31)有3个未知数σ1,n+1、Δλ1和Δλ2。

若应力回映至l6线上，满足σ2=σ3，式(27)可以写为：

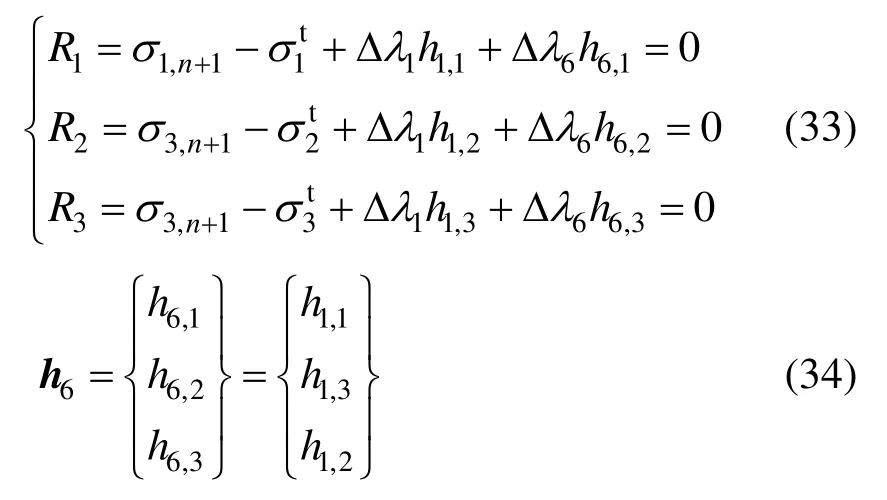
式(33)有3个未知数σ1,n+1、Δλ1和Δλ6。

若上述结果均不满足，当应力回映到尖点处时，更新应力状态满足σ1,n+1=σ2,n+1=σ3,n+1=σa，此时需要求解方程组：

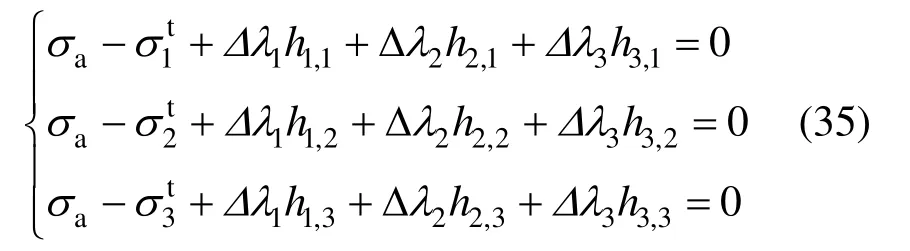
按照式(28)的形式建立Newton-Raphson求解式，分别对式(31)、式(33)和式(35)进行求解，即可求得更新应力值σn+1。

步骤3.损伤修正

由式(10)对损伤变量进行更新：

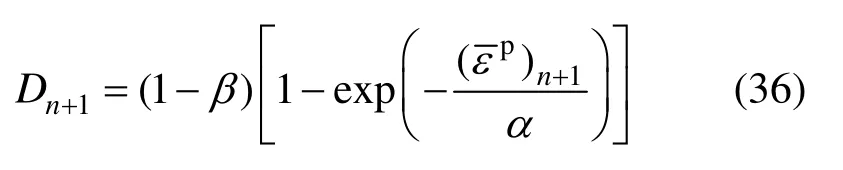
因此，tn+1时刻的所对应的名义应力张量为：

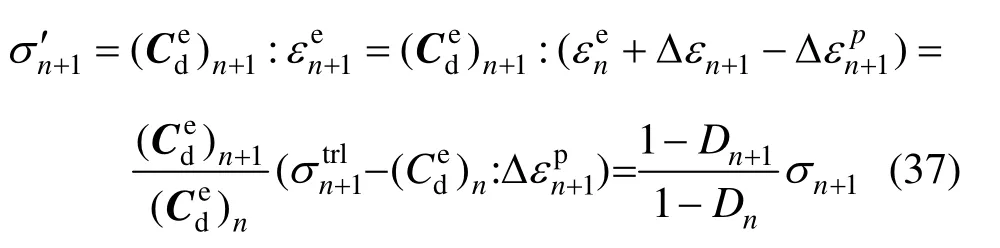
2.2 一致切线模量

为了保证有限元方程组整体迭代求解过程中具有二阶收敛速度，需要给出一致切线模量的表达式：

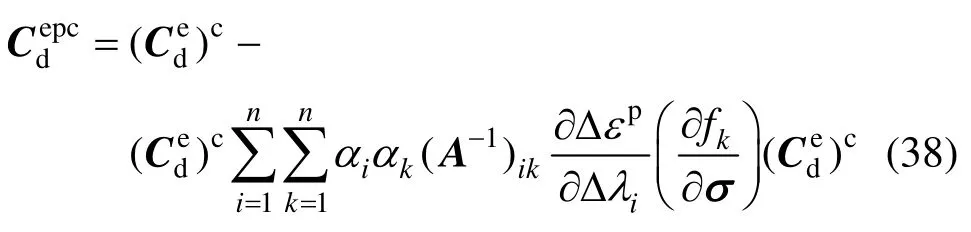
式中：n为屈服函数值大于零的屈服函数个数；Δεp为塑性应变增量；Δλi为塑性因子增量；A为n阶方阵：

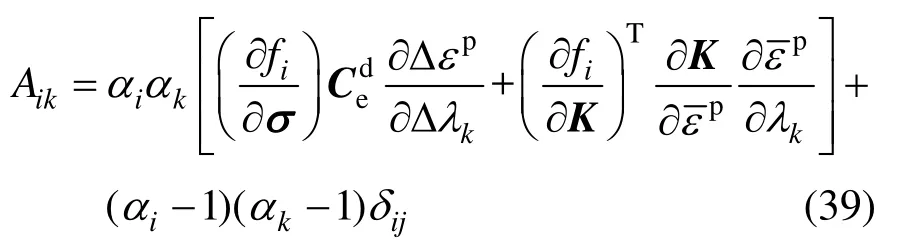
式中：δij为Kronecker符号；αi的表达式为：

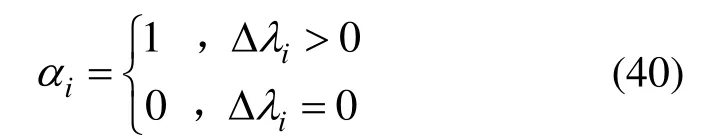
()c为修正弹性矩阵，为修正矩阵，表达式为：

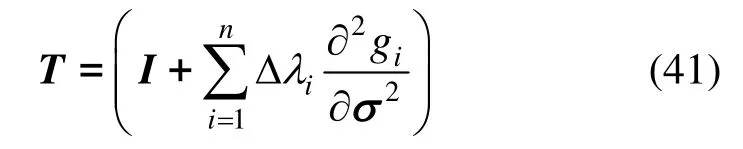
式中，I为单位矩阵。

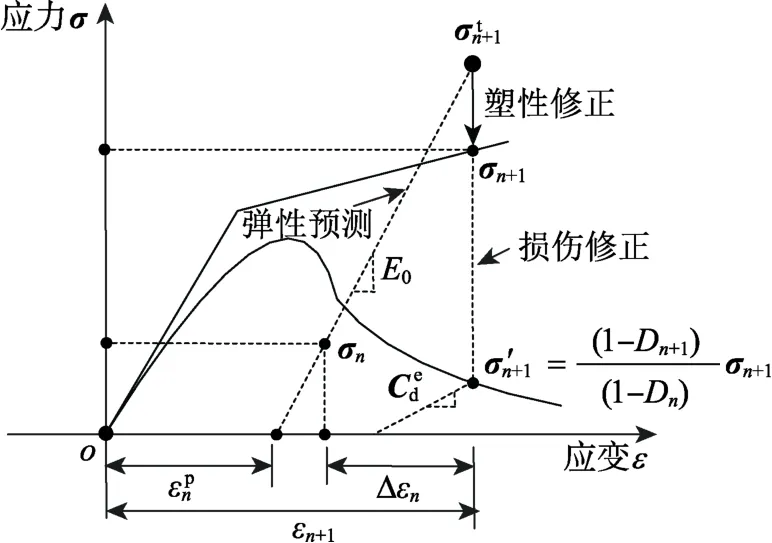
图5 弹塑性损伤模型应力回映算法求解过程Fig.5 Stress mapping algorithm solution process for elastoplastic damage

3 弹塑性损伤模型验证

3.1 试验验证

为验证本文模型的合理性，对室内常规岩石力学试验进行有限元模拟和结果对比。岩石试样取自吉林省辉白隧道，其围岩主要组成为混合片麻岩，包含长石、石英和各种暗色矿物(云母、角闪石、辉石等)，其中长石和石英含量大于50%。将同一掌子面的岩块取回至实验室，然后采用姜堰市星光机电厂生产的ZS-200型自动取芯机取芯，再用SHM-200双端面磨石机打磨加工制成直径50 mm、高100 mm的圆柱状标准试样。试验装置采用大连海事大学和长春朝阳试验机厂联合研制的多功能RLW-2000岩石三轴仪，试验过程采用位移加载模式进行，加载速率为0.002 mm/s。根据文献[29]的研究，由常规三轴和单轴试验获取数值计算参数如下：弹性模量E=21.34 GPa，泊松比ν=0.2，重度γ=24 kN/m3，单轴抗压强度σci=63 MPa，采用关联流动法则对塑性流动特性进行描述，强度参数mbini=mg=3，sini=sg=0.15，a=ag=0.5，残余强度mbfin=0.05mbini，sfin=0.05sini，破坏时的塑性剪切应变γfin=1×10-3。根据峰后段拟合损伤参数α=6×10-4，β=0.45。计算不同围压下岩石应力-应变曲线如图6所示。

由图6可知，不同围压下，数值计算所得岩体峰值偏应力分别为68.96 MPa、72.41 MPa、78.65 MPa和90.60 MPa，与试验所得数值68.90 MPa、70.89 MPa、77.87 MPa和90.01 MPa十分接近，峰后软化段的应力大小与残余强度值的选取有关。

在不考虑围压的情况下，本文模型对不同mb、s值下计算的岩石应力-应变曲线的变化规律研究见图7。由图7可知，随着s的增大，岩石应力应变曲线发生上移，峰值强度随之增大；改变mb的取值对岩石应力-应变曲线影响较小。这与文献[30]的研究结论具有较好的一致性。

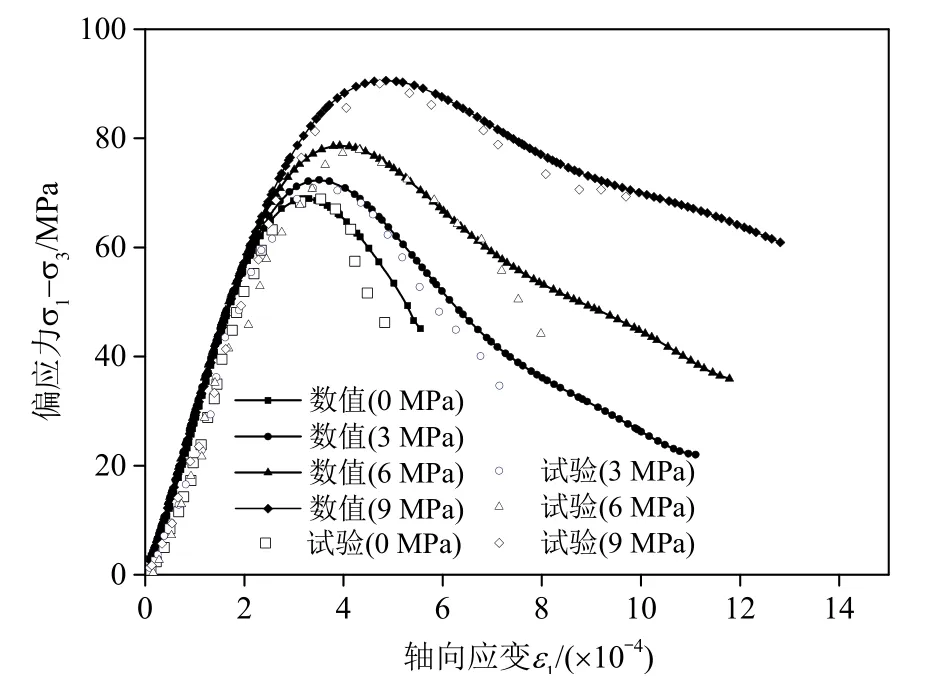
图6 试验曲线与弹塑性损伤模型计算曲线对比Fig.6 Comparison of elastoplastic damage simulations and experimental results

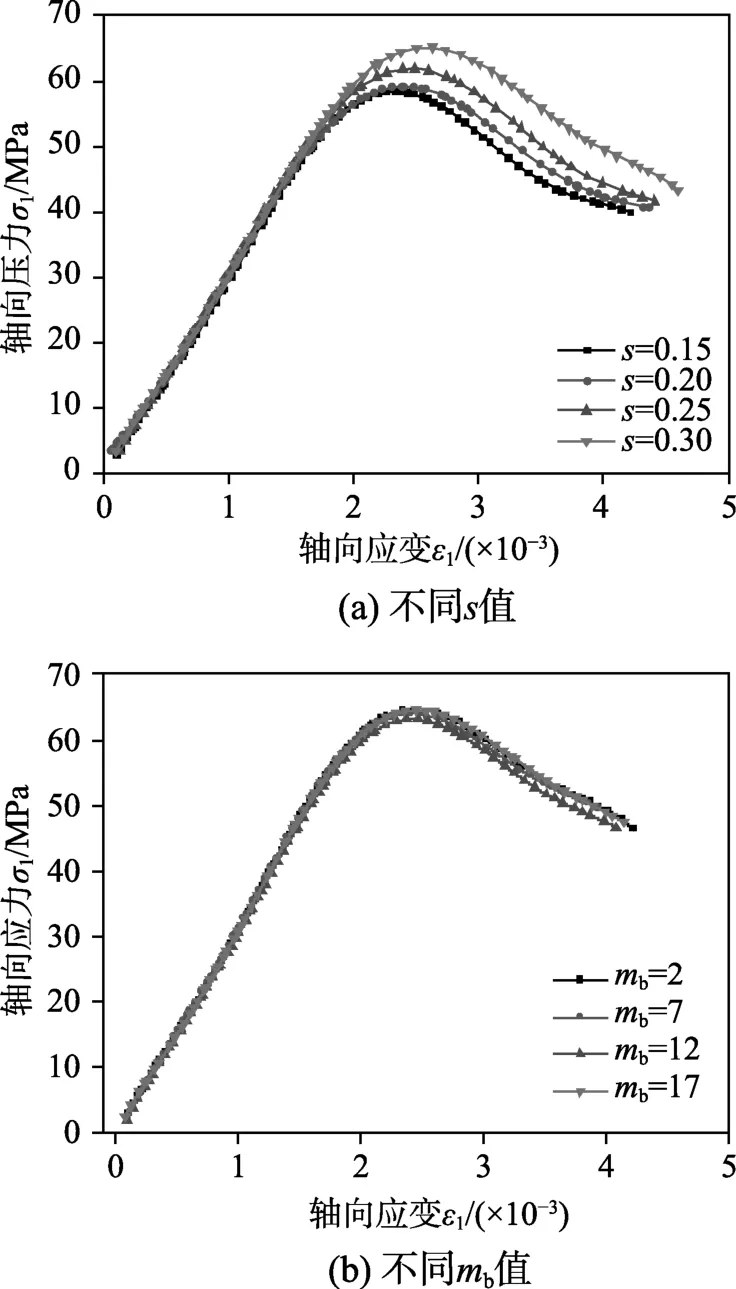
图7 不同s、mb值下单轴抗压应力-应变计算曲线Fig.7 Uniaxial compression curve under different s, mb values

3.2 模型收敛特性验证

为分析所建模型在求解过程中的收敛效率问题，通过Message file文件对图6中围压为零的试件压缩计算过程进行记录。计算过程分为11个增量步，平均每个增量步中含有2.90个迭代步，由于篇幅所限，只记录8、9和10增量步迭代过程中的最大残余力变化规律，如表1所示(收敛标准为默认值5.0×10-3)。

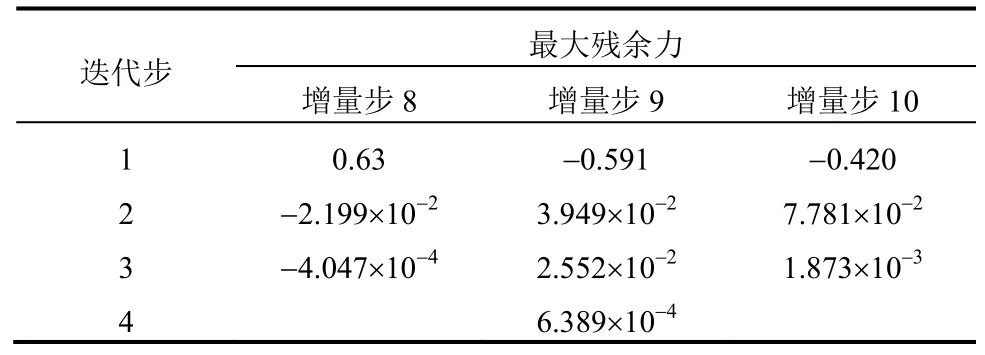
表1 最大残余力变化规律Table 1 Largest residual force change law

由表1可知，一致切线模量的引入使得计算过程具有二阶或接近二阶的收敛速度，保证了模型在实际应用过程中的数值稳定性。

4 工程应用

4.1 工程概况

大连地铁五号线04标段工程起止里程为YK10+061.992～YK12+932.454，其中海域段长度为2310 m。本文所选研究段位于K12+400～K12+753，由地勘报告可知，该段主要穿过中风化白云质灰岩、少量中风化板岩，海水深度约9 m～14 m，海底距隧道顶部约为29.5 m。区间采用土压平衡式盾构机，实行单洞双线双层衬砌的开挖方案，管片内径10.8 m、外径11.8 m、环宽2.0 m、管片厚度50 cm。

4.2 有限元计算模型

盾构施工是一个复杂的三维问题，包括地应力初始平衡、土体开挖、开挖面土体应力释放、盾构机行进、管片衬砌安装、盾尾注浆压力、注浆层硬化等施工过程。每一掘进步的施工流程如图8所示。

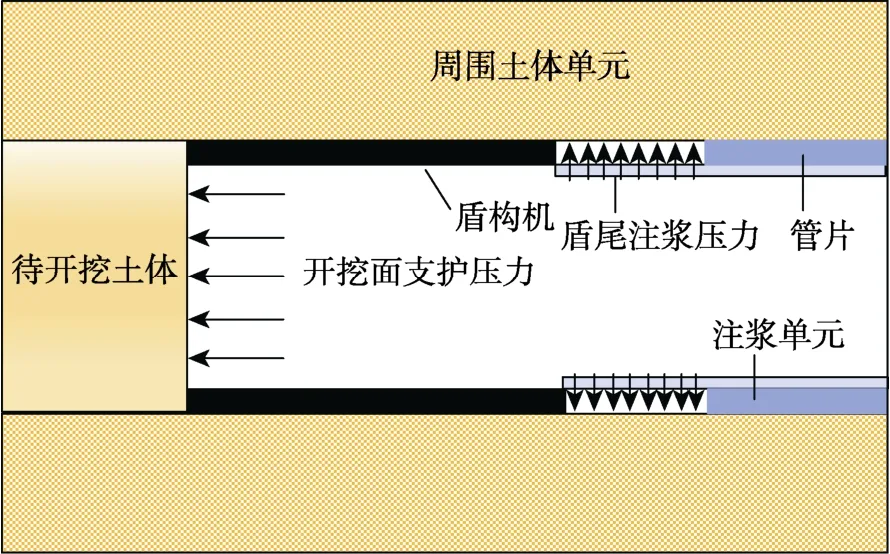
图8 盾构施工流程Fig.8 Shield construction process

根据实际工程概况建立有限元模型如图9所示。模型大小为60 m×30 m×60 m，共划分为17640个单元和17568个节点。管片厚度0.5 m，注浆层厚度0.1 m，开挖半径5.9 m。数值模拟段主要穿过中风化白云岩，依据地勘情况并查阅文献[13]中所提供的表格确定岩体力学参数和主要支护参数如表2所示，mb与s的残余强度均取为峰值强度的1/10，破坏时的塑性剪切应变γfin=1×10-3。模型两侧施加沿z轴方向成线性变化的孔隙水，设置最大水头压力分别为1.5 MPa、3.5 MPa(实际工况)和4.5 MPa。盾构机经过27个开挖步，由y=0 m推进至y=45 m。

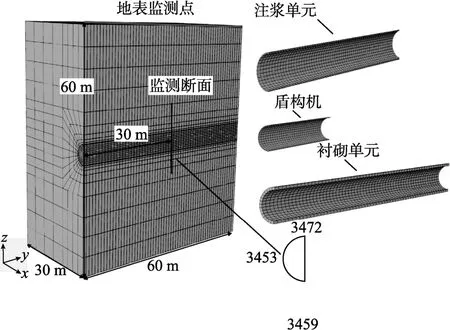
图9 有限元计算模型Fig.9 FEM calculation model

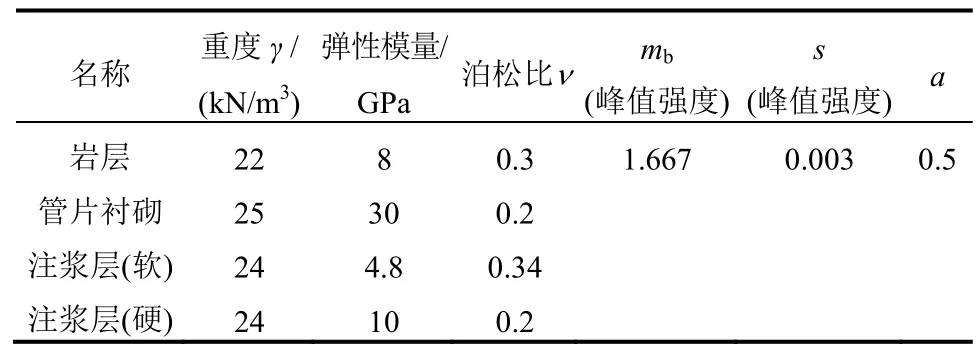
表2 模型计算参数Table 2 Calculating parameters of model

4.3 数值结果分析

由2.2节可知，损伤参数α和β控制了损伤变化速率和最终损伤值的大小。不同损伤参数下，计算出的岩体材料刚度退化程度也不同，为研究损伤参数对数值模拟结果的影响，计算不同α、β下，由y=0 m至y=45 m模型开挖完成后，地表沉降值如图10所示。

由图10(a)可知，地表沉降值随着β的减小而增大，当β=0.5时，计算出现不收敛。由图10(b)可知，随着α的增大，地表沉降值不断减小，当α＞0.05时，沉降值几乎不再发生变化。计算结果表明，损伤参数的选取对计算结果影响较大，模型进行工程应用时宜首先根据监测数据对损伤参数进行反演，获得合理的取值，从而保证计算结果的准确性。

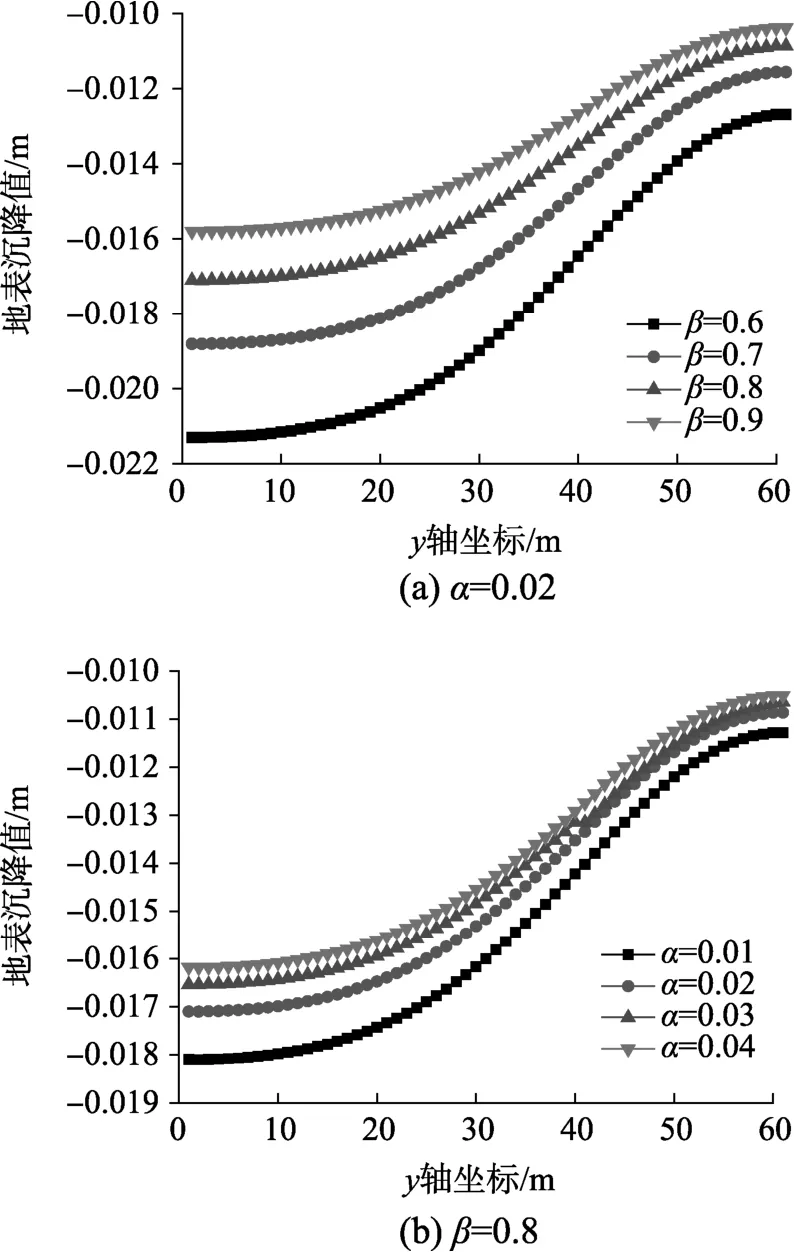
图10 不同损伤参数下地表沉降值Fig.10 Ground surface settlement under different damage parameter

本文选用差异进化算法(DE)对损伤参数进行反演，首先建立基于位移值的目标函数：

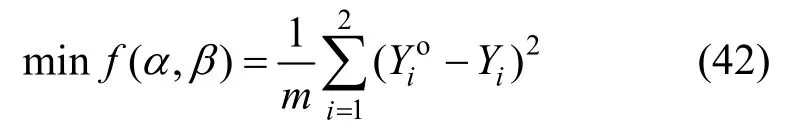
然后通过MATLAB语言反复调用DE算法和ABAQUS求解器对目标函数式(42)进行寻求，最终获得较为合理的损伤参数，具体方法见文献[31]。为保证结果的唯一性，本文选取了3个断面处共9个监测点的数据进行反演，最终得到损伤参数为α=0.002，β=0.51。

不同孔隙水压下，计算开挖损伤区分布情况如图11所示。随着外部孔隙水压的增大，隧道最终开挖损伤区逐渐增大，最大损伤值由2.992×10-3增至3.00×10-3。计算结果表明，孔隙水的存在威胁了隧道开挖稳定性，尤其对于海底隧道，涨落潮过程中，地下水位易发生变化，造成围岩损伤加剧，引发工程事故。

图11 不同孔隙水压下损伤区分布图Fig.11 Damage profile under different pore pressure

图12为最大孔隙水压值为1.5 MPa、3.5 MPa、4.5 MPa的开挖过程中监测断面节点上(参照图9中的标注)的损伤值和位移值变化情况。

由图12可知，盾构施工过程中，监测断面处的损伤值逐步增长，变化速率随着开挖面的临近不断增大，当开挖面远离监测断面时，损伤累积速率逐步减缓，最终变为零，损伤值也不再发生变化。同一监测点处的最终损伤值随着孔隙水压的增大而加大，不同开挖步下的损伤增长速率不同。随着孔隙水压的增大，拱顶点处的最终损伤值分别为0.2988、0.2998和0.2999；拱底点处的最终损伤值分别为0.2980、0.2997和0.2995；拱腰点处的最终损伤值分别为0.2698、0.2861和0.2928，因此可知，孔隙水压的存在加剧了围岩的损伤程度。而在相同水压下，最终损伤值总有拱顶点＞拱底点＞拱腰点，建议在施工监测时严密关注拱顶处是否有衬砌开裂的情况。

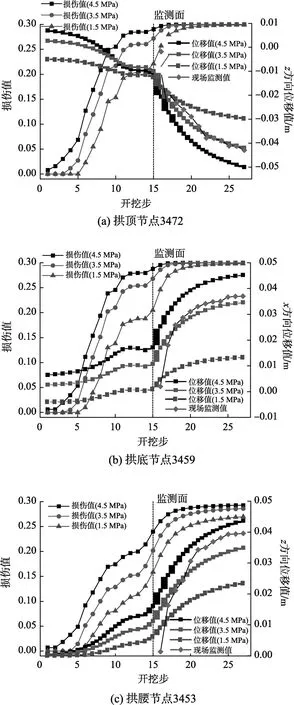
图12 监测点损伤值和位移值变化曲线Fig.12 Monitoring damage and displacement values change curve

由位移计算结果可知，盾构掘进过程中，位移变化速率在临近开挖面时会突然增大，随着开挖面的远离速率不断减小，位移值变化趋于稳定。不同位置处的位移变化形式不同，拱顶监测点主要产生沉降，拱底监测点主要产生隆起，而拱腰监测点主要产生收敛现象。随着孔隙水压的增大，拱顶点处的最终位移值分别为0.0296 m、0.0420 m和0.0500 m；拱底点处的最终位移值分别为0.0133 m、0.0345 m和0.0451 m，拱腰点处的最终位移值分别为0.0234 m、0.0348 m和0.0436 m。各点处位移值均会受到孔隙水压的影响，因此在施工过程中，应紧密关注监测点位移值变化情况，避免海水涨落引发的水压变化对工程造成危害。

由于监测点布设技术的限制，只能对监测面开挖后的监测数据进行统计，但由图12可看出，位移值变化规律与孔隙水压为3.5 MPa(实际工况)时的计算值较为吻合，表明所建模型的计算精度能够满足工程需要。

本文所建弹塑性损伤模型能够计算得到盾构掘进过程中岩体的损伤值和位移变化规律，可以为盾构施工参数(掘进速度、注浆压力和土仓压力等)合理调整提供依据。

5 结论

本文建立了基于H-B准则的岩体弹塑性损伤模型，并给出了模型的数值积分算法。对该模型进行了试验验证和工程应用，得出以下结论。

(1) 本文引入修正有效应力原理来考虑孔隙水压力的作用，建立了基于HB准则的岩体弹塑性损伤本构模型。既具有强度非线性的优点，又能考虑损伤引起的刚度退化和塑性导致的流动两种破坏机制的耦合作用。

(2) 为解决HB弹塑性准则应力空间奇异点导致难以数值求解的问题，本文从主应力空间出发，推导了HB弹塑性损伤模型的包括弹性预测、塑性修正和损伤修正三个步骤的隐式返回映射算法。并通过ABAQUS软件的用户子程序接口Umat成功开发了程序。

(3) 通过试验验证了本模型的合理性。基于建立的HB弹塑性损伤模型和程序，对大连地铁工程的海底盾构隧道进行了三维数值计算，能够合理地反映盾构施工工序、不同海水水压导致的围岩位移和损伤演化规律。计算结果可以为盾构施工参数的合理调整提供依据。