基于修正AIAD模型的稳压器波动管CCFL现象数值模拟

赵柏阳 李 冬 杨已颢 张永祺

（上海电力大学 能源与机械工程学院 上海 200090）

气液相向流动限制现象（Counter-Current Flow Limitation，CCFL）［1］对于压水堆核电厂的安全分析十分重要，失水事故［2］后，当向上流动的气相速度足够大时，会部分或完全地阻碍液相向下流动。该现象机理复杂，受汽液两相流速、流道几何结构、压力空泡份额等多种因素影响，在第三代核电技术发展以前，研究主要集中于对热管段、压力容器下降段等竖直管或倾斜管内的实验及理论分析。Wang［3］、Kim［4］和Navarro［5］等研究了管径、流速、倾斜角等因素对直管、倾斜管中CCFL现象的影响，并通过实验数据拟合出公式用于预测CCFL现象。近年来，由于自动泄压系统的引入，事故后稳压器波动管中的CCFL现象增加了安全风险。稳压器波动管结构则更为复杂，同时包含了竖直管、倾斜管及螺旋弯管，一维系统程序的模型研究对复杂三维结构并不足够。Takeuchi等［6］、Doi［7］通过实验对稳压器波动管CCFL现象进行研究发现，发生CCFL现象最剧烈的位置位于竖直管段，而对弯管内的现象分析仍不明确。Murase［8］使用传统流动模型对 Futatsugi［9］的实验台架进行了三维数值模拟，模拟结果与实验数据相比存在一定偏差。因此有必要对稳压器波动管的CCFL现象的相间作用模型及流动特性进行更深入的研究。

基于CCFL现象机理及汽液相间作用的影响，本文使用ANSYS CFX程序，选择自由表面模型结合（Algebraic Interfacial Area Density，AIAD）模型对稳压器波动管CCFL现象进行三维数值模拟，并基于网格影响对AIAD模型进行了修正，通过模拟结果和实验现象的对比来验证模型，并进一步探究稳压器波动管的CCFL特性以及几何结构的影响。

1 计算模型

1.1 自由表面模型

CCFL现象发生时常伴有阻塞形成、液滴夹带、水力跳跃等现象，这些现象会引起相间作用力的变化。相间作用可以通过界面剪切应力描述，不同流型下的气液两相之间的界面剪切应力可以由自由表面模型求得。

在三维模拟计算中，求解了两流体模型的质量方程和动量方程，其形式如下：

式中：下标k代表气相或液相；ρ为密度；U为速度矢量；t为时间；p为压力；g为重力加速度；r为体积分数；τ为剪切应力（τυ为平均粘性剪应力τt为湍流剪应力）；τD为界面剪应力。式（2）等号右边第一项为压力项，第二项为重力项，第三项为平均粘性剪切应力和湍流剪切应力项，第四项为界面剪切应力项。自由表面模型主要通过求解界面剪切应力来描述相间作用关系。

界面剪应力τD可表示为流体流动过程中总的阻力与界面面积密度的比：

式中：FD为流体流动过程中的总阻力；A是界面面积密度。

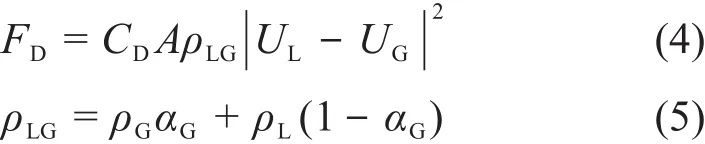
式中：ρLG是平均密度；|UL-UG|是相对速度；CD是无量纲的界面摩擦阻力系数。

在自由表面流动的模拟中，式（4）不能代表一个真实的物理模型。假设在界面附近的两种流体的速度是相似的。因此从两相表面附近假定一个类似壁面剪应力的剪应力，以减小两相的速度差，沿“固体”状边界运动的粘性流体会产生剪切应力，在无滑移条件下，自由表面区域为边界层，剪切应力的计算表达式可写成以下形式：

式中：AFS为自由表面的界面面积密度。对于气泡和液滴来说，有固定的公式来描述界面面积密度，但是在实际流动过程中流态常常介于气泡和液滴之间，在这里我们加入AIAD模型根据不同气液相体积分数来代数化求解AFS，这样可以通过气液相体积分数的变化得到不同的界面摩擦系数，更好地描述流动的特征。

1.2 修正的AIAD模型

原始AIAD模型［10］采用了三种不同的阻力系数：下标B、D、FS分别表示气泡、水滴、自由表面。界面面积密度A也与相的形态有关。对于泡状流型：

式中：rG为气相体积分数；dB为气泡直径。

对于自由表面：

根据式（3）、（4）、（7）、（9）得到：

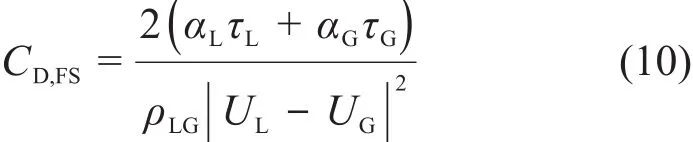
界面面积密度的简单切换过程使用混合函数f。该函数引入空泡份额率极限、流态权值以及气泡和液滴流动的长度尺度，定义为：

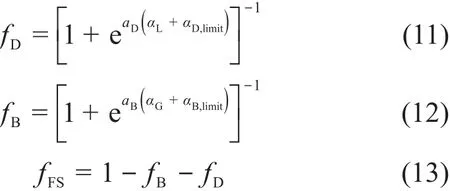
界面面积密度和阻力系数分别定义为：

根据经验值αD，limit=αB，limit=0.3，aD=aB=70。CD，B=CD，D=0.44。

本文在传统AIAD模型的基础上对混合函数f的表达式进行了修正，目的是为了使混合多种影响因素后总的阻力系数随着局部流动特征引起的不同参数而变化，这样可以避免因为经验值选取不当而导致的计算偏差。为便于区分，函数用φ来表示。

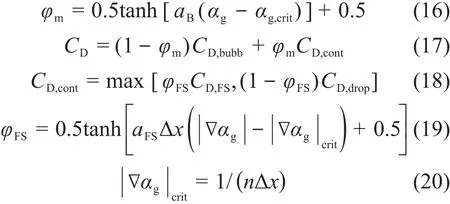
式中：φm代表气泡的混合函数表达式；αg，crit=0.3，CD，cont是变量系数；CD，bubb=CD，drop=0.44，|∇αg|是空泡份额梯度；Δx表示单位网格尺寸；这里aFS取100，n取4。

该模型可以通过体积分数来判断出局部的流动形态［11-12］（表1）。

表1 体积分数和相应的形态Table 1 Volume fractions and corresponding morphologies

2 数值模型建立

2.1 几何构建和边界条件设置

本文以文献［9］中的1/10比例的AP600稳压器实验为参考，建立对应的几何模型。实验装置如由一个倾斜管（倾斜角θ=0.6°～5°）、一个竖直弯头和一个垂直管组成。管径D=30 mm，空气入口速度JG，in范围为 0～5.5 m·s-1，JL，in液相入口速度始终为0.07 m·s-1。三维模拟所建立的几何模型尺寸均与实验装置相同。进出口边界设置如图1所示。

图1 几何模型及边界设置Fig.1 Geometric model and boundary setting

三维数值模拟计算通过ANSYS CFX软件来实现，数值计算在瞬态模式下运行。在网格独立性研究中，对三种不同精度的网格进行了比较。对于最粗网格（网格数量为40 000节点）没有达到收敛，对节点数量为130 000和500 000的网格的主流方向速度分布进行了分析，结果表明：两种数量的网格主流方向速度分布没有定性差异，定量偏差最大小于1%，因此使用节点数量为130 000的网格来完成计算。在建模中选用SST浮力湍流模型，对流项采用高阶离散格式，对于时间积分，采用完全隐式二阶倒推欧拉法，时间步长Δt=0.001 s，每个时间步长最大循环次数为10次。收敛性定义为残差的RMS的值要小于10-4。

气液相是等温不可压缩的，利用重力方向项考虑了两相之间的浮力效应。两相均采用5%的湍流强度。空气出口设为开口边界，整个物理过程在常温常压下进行，管内视为光滑且壁面无滑移条件。界面摩擦阻力系数由修正后的AIAD模型决定，该模型通过ANSYS CFX控制语言编入程序。

2.2 与实验现象对比

稳压器波动管结构复杂，发生CCFL现象的位置也较多，主要有CCFL-L、CCFL-S、CCFL-U三个位置。CCFL-L和CCFL-U发生的几何结构分别与倾斜直管段和竖直管段相似，而CCFL-S现象是稳压器波动管特有的，这里重点关注CCFL-S现象。由于气相速度的增大，会对液相的流动形成阻力，当气相速度足够大时，液相无法继续按照原方向流动甚至向相反的方向流动，进而形成阻塞，沿着管道逆向推进，直至达到一个平衡的状态。通过数值模拟的结果（图2）可以明显地看到，阻塞推进到波动管弯头位置，并伴有水跃现象，这是典型的CCFL现象。这定性地说明修正过的AIAD模型可以模拟出CCFL现象，选取实验中典型的工况和位置来验证模拟结果的准确性，当θ=0.6°，JG，in=3.8 m·s-1，JL，in=0.07 m·s-1时，液相反向流动，发生CCFL现象，实验现象如图3（a）所示，模拟结果如图3（b）所示。模拟结果与实验现象吻合证明了AIAD模型对于稳压器波动管CCFL现象的相间作用模拟的准确性。

图2 波动管波峰推进图Fig.2 Wave peak propulsion diagram of surge line

3 计算结果分析

本文选取了稳压器波动管上10个关键位置节点（图4）。这些位置都是弯管的入口和出口部分，因为流体经过一个弯管时，流道角度变化大，通常在这样的位置更容易发生CCFL现象。

图3 倾斜管段实验现象(a)和模拟结果(b)Fig.3 Experimental phenomena(a)and simulation results(b)of the inclined pipe

此外反应堆中流道的阻塞会引起流体流动速度的分布发生变化，流动速度分布不均匀会引起局部换热能力下降和压力分布恶化等，而流道压力分布的变化会在局部造成压力过大，影响管道的安全性。通过对10个关键位置的抽取数据来定量分析气相流速、波动管倾斜角对阻塞形成和推进的影响。

图4 节点位置Fig.4 Node location diagram

本次模拟计算中，对不同初始气体速度条件下阻塞形成位置和推进情况的数据进行对比，如图5所示。图5中L代表所选位置与管道起始点的距离，管道全长1.9 m，从右至左5条曲线分别代表5种从低到高的初始气相流速。曲线上由低到高不同的点代表10个关键位置。通过对比可以得到：

1）从整体来看，初始气相流速越大，阻塞推进到各个关键位置的时间越短，速度越快。对于靠近管道起始点的位置（位置1、2、3），当初始气相流速足够小的时候，阻塞在相邻两位置点的推进速度并无明显差异；但是在初始气相流速增大到一定程度时（如方块点构成的折线），位置1、2处将不会出现阻塞，这说明在位置1、2处气相流速占主导地位。

2）对于远离管道起始点的位置4～10，只考虑气相流速的增加的影响，应该出现位置8～9阻塞推进比位置6～7更快的现象。但是由于倾斜角导致的位置8～9高度的变化，出现了位置6～7阻塞推进更快的现象，这说明在位置4～10高度变化占主导地位。

图5 不同速度对阻塞形成和推进的影响Fig.5 Effects of different velocities on slug formation and propulsion

阻塞推进受初始气相流速和倾斜角的复合影响，在气体初始流速相同的情况下，本文分别选取倾斜角θ=0.6°、θ=2.5°、θ=5°时的数据进行对比分析（图6），得到：

1）整体来看，在气相流速不变的情况下，波动管倾斜角越大，阻塞形成时间越晚，推进速度越慢，相邻节点之间推进时间间隔长。对于位置1～3，θ=0.6°、θ=2.5°、θ=5°三种情况下阻塞形成时间随倾斜角度增加而推迟，但是推进速度大致相同（斜率大小基本一致），这说明倾斜度对靠近管道起始点的位置，即高度变化小的位置的阻塞形成时间有影响，但对推进速度影响不大。

2）对于位置4～10，在气相流速不变的情况下，随着倾斜角度的增加，阻塞推进速度明显减慢，θ=5°时阻塞甚至推进不到位置10就达到了平衡。这是由于随着管长增加，倾斜度越大引起的高度变化而导致的。

图6 不同倾斜角度对阻塞形成和推进的影响Fig.6 Effects of different inclined angle on slug formation and propulsion

4 结语

本文使用ANSYS CFX软件对稳压器波动管中CCFL现象进行三维数值模拟，并以经典实验数据为参照标准，来探究CCFL现象的特性。为了更好解释CCFL现象，模拟过程使用自由表面模型，并且加入修正后的AIAD模型。通过对计算结果数据的处理，得到了不同初始气相流速、不同稳压器波动管倾斜角度下阻塞推进的规律：

1）倾斜角度一定的情况下，初始气相流速越大，阻塞向前推进的速度越快。

2）在气相流速不变的情况下，波动管倾斜角越大，阻塞形成时间越晚，推进速度越慢，相邻节点之间推进时间间隔长。

3）在靠近管道起始点的位置，即高度变化小的位置，阻塞推进主要受初始气相流速的影响；在远离管道起始点位置处，阻塞推进主要受倾斜角度的影响，这是由于高度变化大而导致的。