初中数学教学学生探究能力的培养初探

张俊丽

【摘要】 新课程改革注重学生学习方式的改革，并且探究性学习也已经越来越受重视.初中数学教学中，教师可以通过优选探究问题，创设实践情境，延伸探究时空的方法，激发学生探究的兴趣，营造学生探究的良好氛围，让探究成为学生的一种习惯.

【关键词】初中数学;探究能力;优选;创设;延伸

新课程改革注重学生学习方式的改革，并且探究性学习也已经越来越受重视.教学中，教师既要激发学生探究学习的热情，更要有效地引导学生学会探究.《义务教育数学课程标准（2011年版）》指出：学生学习应当是一个生动活泼的、主动的和富有个性的过程.认真听讲、积极思考、动手实践、自主探索、合作交流等，都是学习数学的重要方式.美国心理学家布鲁纳也指出：探究是数学教学的生命线.初中数学教学中，如何培养学生的探究能力呢？本文从以下三个方面谈一些粗浅体会.

一、优选探究问题，激发学生探究的兴趣

美国著名数学教育家G·波利亚说：“一个专心的认真备课的教师能够拿出一个有意义的但又不太复杂的题目，去帮助学生发掘问题的各个方面，使得通过这道题，就好像通过一道门户，把学生引入一个完整的理论领域.”所以，探究问题的选择直接影响探究活动的质量和效果.问题过于简单，就会缺乏思维的挑战性，探究活动可能华而不实;探究问题过于复杂，从中受益的学生寥寥无几，探究活动最终流于形式.

事实上，对于课本中的例题、习题，教师若能引导学生从不同的知识侧面，用不同的思维方式进行探究，增强解题灵活度，便能通过“一题多解”，强化知识间的横向联系，让学生做一题，明白一串道理，巩固一串知识，培养一串能力，掌握一串处理问题的方法.

例如，人教版八年级下册数学课本第46页有一道例3，题目如下：

如图1，ABCD的对角线AC，BD相交于点O，E，F是AC上的两点，并且AE=CF.求证：四边形BFDE是平行四边形.

授课时，笔者引导学生从不同角度分别应用平行四边形的五个判定定理来探索出不同的五种证法，让学生在比较不同证法的难易中，明确此题用“对角线互相平分的四边形是平行四边形”这一判定定理最为便捷，进而通过这道题的一题多证，扩大教材知识点的覆盖面以及联系，从而深入挖掘教材例题的内涵.

在此基础上，笔者对该例题进行了以下变式：

变式1： ABCD的对角线AC，BD相交于点O，点E、点F是AC上的三等分点.求证：四边形BFDE是平行四边形.

变式2：ABCD的对角线AC，BD相交于点O，点E、点F分别是OA，OC的中点.求证：四边形BFDE是平行四边形.

变式3：ABCD的对角线AC，BD相交于点O，若E，F在AC的延长线上，且AF=CE.则四边形BFDE仍是平行四边形吗？

以上三个变式题中，四边形ABCD和四边形BFDE有一条共同的对角线，另一条对角线在同一直线上，因此，在证题时，综合运用“平行四边形的对角线互相平分”“对角线互相平分的四边形是平行四边形”这两条定理来证明更简捷.这样通过“一题多变”， 纵向深入挖掘知识内涵，激发学生探究的热情，从而实现了抓住“一例”，涉及“一片”的教学效果，对于培养学生的探究能力，大有裨益.

二、创设实践情境，营造学生探究的良好氛围

苏霍姆林斯基说过：“手和脑之间有着千丝万缕的联系，手使脑得到发展，使它更明智;腦使手得到发展，使它变成思维的工具和镜子.”这充分说明了引导学生动手实践在学习、探究、获得知识的过程中发挥着极其重要的作用.初中数学教学中，教师要把动手实践操作与学生的思维和深层次思考紧密结合在一起，让学生经历数学知识的再发现和再创造的过程，从操作中掌握探究的方法，感受数学知识的形成.

例如，在教完人教版八年级数学上册“轴对称”章节内容后，笔者曾开设了一堂折纸数学实验课，具体实践操作情境设计如下：

活动1： 如图2，一张矩形纸片ABCD，请学生任意折起一个角，折痕为EF，用笔将折痕和重叠部分的边描出，再展开图进行探究.

（1）折叠前后的两个三角形△EBF和△EB′F的关系.

（2）折痕EF与对称点连线BB′之间的关系.

（3）探索图中是否存在等腰三角形.

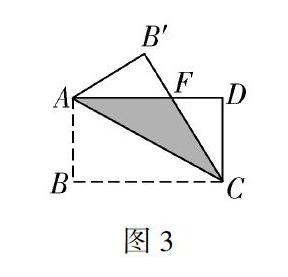
活动2： 如图3，一张矩形纸片ABCD，沿对角线折叠，请学生探究图中是否存在等腰三角形.若有，请予以证明.

活动3：引导学生总结和交流图2、图3中折等腰三角形的方法：①利用“两边相等的三角形是等腰三角形”这一判定方法，通过折叠，得到两边相等，进而得到等腰三角形;②利用“角平分线+平行等腰三角形”这个基本模型，通过折叠得到两个等角，进而得到等腰三角形.

活动4：引导学生继续探究用矩形纸片折出等腰三角形的其他方法，并上台展示和交流如图4、图5、 图6所示的不同的折叠方法.

这三个实践操作情境的创设，引导了学生直观感知、操作确认，并经历折纸中的 “轴对称”这一自主探索和合作交流的过程，较好地拓宽了学生的思维空间，对他们理解和掌握等腰三角形的性质和判定，培养他们的探究能力大有帮助.

三、延伸探究时空，养成学生自觉探究的习惯

一堂课结束并不是探究的终点.为进一步让学生掌握探究的方法，养成自主探究的习惯，培养其终身学习的能力，教师应积极引导学生做好课后延伸探究工作.

例如，上完“中心对称图形”这一节课后，笔者布置了一份探究作业，要求如下：（1）请学生收集日常生活中的中心对称图形;（2）方案设计：学校开辟了一块形如长方形的地，准备建几个花坛，现在全校征稿，要求花坛应该既有圆的造型又有方的造型，同时整个花坛应该既是轴对称图形又是中心对称图形，请设计出你的方案.

学生热情高涨，涌现出不少奇思妙想.这样的课后延伸探究，既让学生更深刻地理解了中心对称图形的概念以及中心对称图形的性质，又很好地培养了学生的探究能力与创新意识.

此外，《义务教育数学课程标准（2011年版）》对于数学模型有非常明确的说明：数学模型的建立是学生体会和理解数学与外部世界联系的基本途径.在初中数学阶段的学习中，学生最怕的就是几何.而几何，看似变化莫测，实则很多题都可以抽象出基本模型.抓住模型，抓住本质，方能以不变应万变.为此，笔者很重视引导学生在课后总结一些常见的几何模型.例如，在教完人教版数学七年级下册“三角形”章节后，笔者就要求学生在完成相应习题的基础上，探究发现、归纳总结出三角形双内角角平分线夹角模型、双外角角平分线夹角模型、一内角一外角角平分线夹角模型、八字模型、飞镖模型、折角模型、三“八”模型等常用的数学模型;在教完人教版数学八年级上册“全等三角形”章节后，笔者引导学生归纳总结手拉手模型、倍长中线类模型、三垂直模型、一线三等角等模型;在教完人教版数学八年级上册“轴对称”章节后，笔者引导学生归纳总结最短路径模型.这些基本几何模型的建立与识别，能够让学生在解决几何复杂图形问题时达到触类旁通、多题归一的效果，同时也有利于提高他们解决问题的能力.学生在探究结论的过程中体验到了几何数学模型在解决实际问题中的价值和作用，有助于他们在课后继续保持探究的热情，养成自觉探究的好习惯.

总之，培养学生探究能力是一个循序渐进的过程.在初中数学教学中，教师要尊重学生的主体地位，积极创设情境，营造学生探究的良好氛围，激发学生探究的兴趣，并在合作交流中呈现学生探究的成果，以培养他们主动参与、乐于探究、交流、合作与实践的意识和习惯，使学生在探究过程中得到必要的数学思维训练，理解并掌握基本的数学知识与技能、数学思想和方法，提高实践能力和创新能力，进而获得可持续发展的动力.

【参考文献】

[1]中华人民共和国教育部.义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2012.

[2] 张柳.数学基本活动的教学研究：例谈“折等腰三角形”的实验设计及教学反思 [J].初中数学教与学，2019（3）：11-14.