基于信息熵的粗糙集连续属性离散检验算法

杨海鹏

(吉林工程技术师范学院 信息工程学院，长春 130052)

通过构建大数据挖掘模型，提高对云计算环境下大数据挖掘和查询的精度，进行大数据特征信息采样，能实现对大数据的远程信息探测和自适应调度，为了提高大数据的分类融合和特征识别能力，需要进行大数据的粗糙集挖掘，建立相关粗糙集连续属性离散数据的特征提取模型，在提高大数据的挖掘和自适应分类能力方面具有重要意义[1].

对粗糙集连续属性离散数据的特征提取是建立在对数据的聚类属性分析基础上，采用自适应特征分类方法，进行粗糙集连续属性离散数据检测，采用特征标注方法构建粗糙集连续属性分布 的特征辨识模型[2]，结合关联规则挖掘方法，实现粗糙集连续属性离散检验.传统方法中，对粗糙集连续属性离散检验方法主要有关联规则挖掘方法、模糊特征提取方法和C 均值聚类方法，建立粗糙集连续属性离散分布模型[3]，采用相关均衡控制方法，进行粗糙集连续属性离散检验.文献[4]中提出一种基于梯度提升回归树的粗糙集连续属性离散数据信息熵离散检验模型，构建粗糙集连续属性离散数据的特征权重分布式检测模型，采用融合相关性聚类分析方法实现数据回归分析，提高数据的信息熵离散检验识别能力，但该方法的计算开销较大，对粗糙集连续属性分布检验的实时性不好.文献[5]中提出基于关联特征分布检测的粗糙集连续属性离散数据离散检验方法，提取粗糙集连续属性离散数据的关联特征分布集和属性集，根据粗糙集连续属性离散数据的属性分布实现特征提取和离散检验，但该方法进行数据特征离散检验的模糊度较大，收敛性不太好.

针对上述问题，提出基于信息熵的粗糙集连续属性离散检验算法，采用特征空间重组方法进行粗糙集连续属性离散数据的模糊特征重构，提取粗糙集连续属性离散数据的信息熵；并对所提取的信息熵进行聚类分析，建立连续属性分布数据的信息熵提取模型，采用模糊聚类方法实现对粗糙集连续属性的离散特征挖掘和聚类分析；最后根据粗糙集连续属性的融合结果，实现离散检验和数据挖掘.

1 数据分布模型及特征分析

1.1 粗糙集连续属性离散数据分布序列特征

为了实现粗糙集连续属性离散数据信息熵离散检验，首先构建粗糙集连续属性离散数据的分布式存储结构模型，采用显著性区域调度方法进行粗糙集连续属性离散数据的信息融合处理；再构建粗糙集连续属性离散数据优化调度和特征提取模型，进行粗糙集连续属性离散数据的自适应离散检验[6]；分析粗糙集连续属性离散数据的离散空间调度模型，采用模糊链路控制方法，进行粗糙集连续属性离散数据的融合调度，得到粗糙集连续属性离散自适应加权权重为

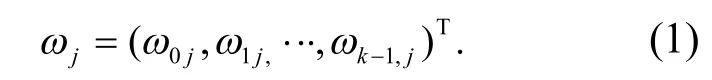
通过对粗糙集连续属性特征分析，构建粗糙集连续属性离散数据的统计特征分布样本集为

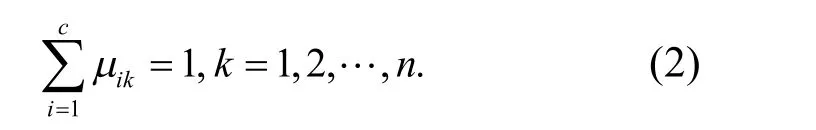
其中，k为粗糙集连续属性离散数据的灰度空间分布权重.采用离散序列调度方法，构建粗糙集连续属性离散数据的特征匹配模型[7]，根据多分量检测方法进行粗糙集信息离散检验，实现粗糙集连续属性离散检测，得到检测统计量为

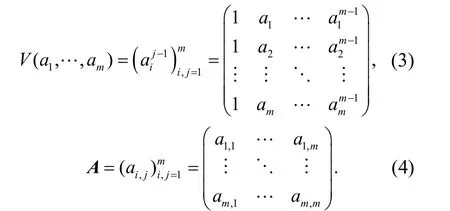
根据特征谱的聚类权重进行模糊自适应聚类处理，构建粗糙集连续属性离散数据分布的有限数据集模型[8]，得到粗糙集连续属性离散调度的关联特征为

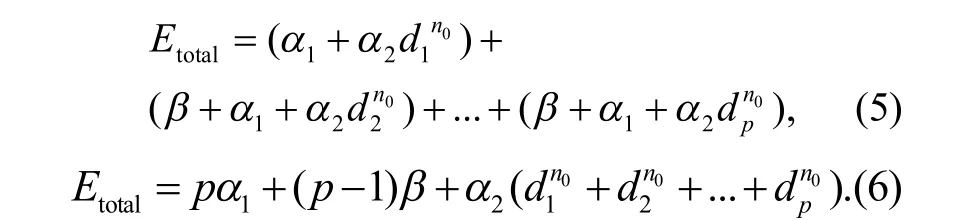
在分散子空间中进行粗糙集连续属性离散数据的特征重构[9]，构建粗糙集连续属性离散数据的统计分布序列特征矩阵满足

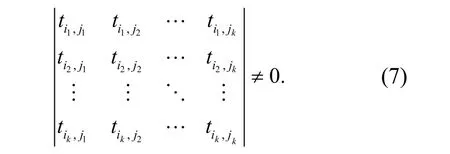
采用决策树模型，构建粗糙集连续属性离散数据的空间聚类模型.

根据上述分析，可得到粗糙集连续属性离散数据分布结构模型如图1 所示.

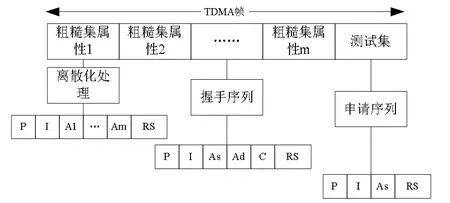
图1 粗糙集连续属性离散数据分布结构模型

1.2 离散数据闭繁项关联分析度量

采用特征空间重组方法进行粗糙集连续属性离散数据的模糊特征重构，提取粗糙集连续属性离散数据的信息熵，采用决策树算法进行粗糙集连续属性离散数据信息熵离散检验，得到量化特征分布集定义为D，D=｛S i,j（t） ,Ti,j（t） ,U i,j（t）｝.其中，S i,j（t）表示粗糙集连续属性离散数据特征权重的重复因素；Ti,j（t）表示粗糙集连续属性离散数据信息熵离散检验的输出量因素；U i,j（t）表示相似度(相关性)模型.对粗糙集连续属性的离散数据特征权重关联规则特征量进行量化回归分析，定义为

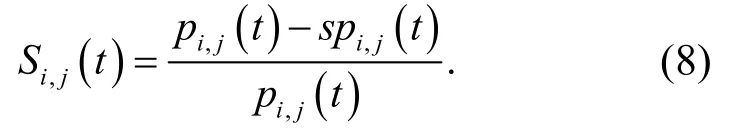
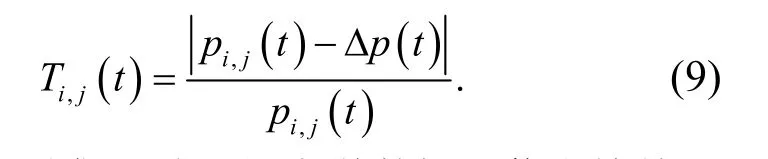
提取粗糙集连续属性离散数据的信息熵特征量，根据信息熵特征提取结果，进行粗糙集连续属性大数据挖掘，得到粗糙集连续属性离散数据的闭繁项关联分析度量值为

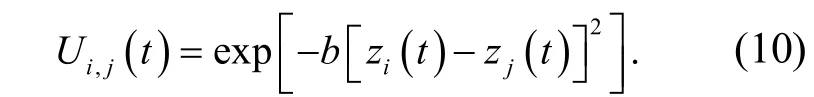
其中，p i,j(t)为粗糙集连续属性离散数据信息熵离散检验的互信息量；sp i,j(t)为粗糙集连续属性离散数据特征权重检测的分叉度重复量；Δp(t)为增益系数；z i(t)，z j(t)表示为粗糙集连续属性离散数据特征权重检测的模糊度函数.

由此建立粗糙集连续属性离散数据的特征提取和信息融合处理方法，并采用模糊C 均值聚类分析方法构建粗糙集连续属性的离散特征分析模型，利用随机数检测方法进行粗糙集连续属性的离散检验[10].

2 粗糙集连续属性离散检验优化

在云计算环境下进行粗糙集连续属性大数据挖掘，采用特征空间重组方法进行粗糙集连续属性离散数据的模糊特征重构，对粗糙集连续属性离散检验优化，主要分为2 个步骤：1)采用粗糙集连续属性关联挖掘方法，进行离散数据特征权重的回归分析，对粗糙集解结构重组；2)提取粗糙集连续属性离散数据的信息熵，对所提取信息熵进行聚类分析，得到粗糙集连续属性离散数据的信息熵特征提取结果，构建粗糙集连续属性离散数据集的特征匹配函数，在数据聚类中心得到优化的粗糙集连续属性离散数据检验输出.

2.1 粗糙集连续属性离散数据空间重组

采用相空间重构方法进行模糊特征重构.用一个四元组（Ei,E j,d,t）来表示粗糙集连续属性离散数据特征权重的统计分布特征量，其中：Ei，Ej是粗糙集连续属性离散数据特征权重的实体集(即节点i和j)；d为粗糙集连续属性离散数据特征权重的交互性统计数据；t为粗糙集连续属性离散数据信息熵离散检验的时间延迟.采用粗糙集特征重构方法[11]，进行统计时间序列分析，得到粗糙集连续属性离散数据特征权重的决策树分布特征量化集为

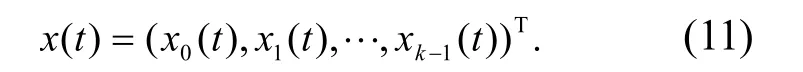
采用一个1×N的矩阵进行粗糙集连续属性离散数据特征权重分类，用离散检验分析方法确定粗糙集连续属性离散数据特征权重的离散检验时间窗口值N，构建多维熵矩阵.在相空间重构模型中，建立粗糙集连续属性离散数据的特征权重分析模型[12]，建立窄时域窗TLX和TLY，得到粗糙集连续属性离散数据特征权重的模糊特征提取模型为

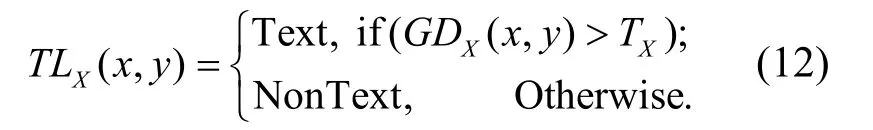
设粗糙集连续属性离散数据特征权重的分布为m，先用信息熵特征分析方法得到粗糙集属性集为 *jN，再采用粗糙集连续属性关联挖掘方法进行离散数据特征权重的回归分析，得到粗糙集连续属性离散数据空间重组为

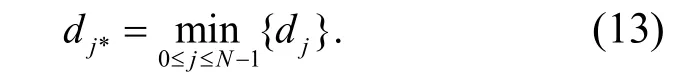
根据粗糙集连续属性挖掘结果，进行离散数据特征分类检测，构建粗糙集连续属性离散调度模型，进行粗糙集解结构重组[13].

2.2 粗糙集连续属性离散检验输出

建立粗糙集连续属性离散数据的信息融合模型，采用大数据挖掘方法进行粗糙集连续属性离散数据空间重组的信息融合，其输出为

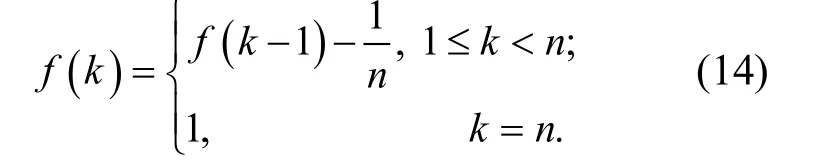
大数据集在节点si处的能量谱密度，采用主成分分析方法构建粗糙集连续属性离散数据特征权重的回归分析模型，采用特征空间重组方法进行粗糙集连续属性离散数据的模糊特征重构和聚类处理，待检验的粗糙集连续属性离散数据按照五元组离散检验，得到粗糙集连续属性离散数据信息熵的分布概率密度特征为

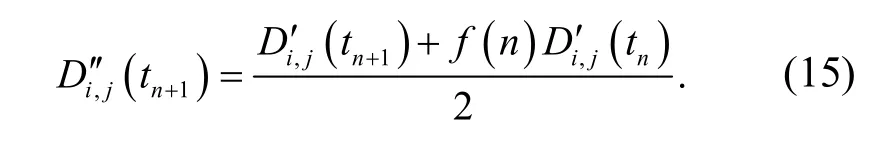
根据粗糙集连续属性离散数据的属性分布构建统计分布量化函数，粗糙集连续属性离散数据特征权重分布的互信息量为

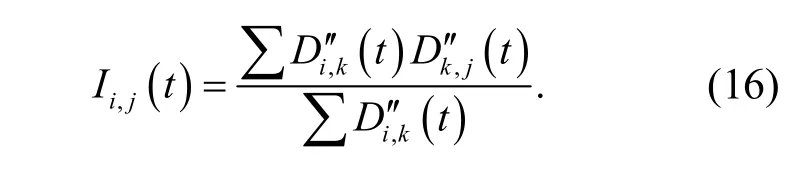
采用关联规则分层调度方法，进行粗糙集连续属性离散数据的信息熵离散检验和可靠性评估，得到可靠性评价函数表述为

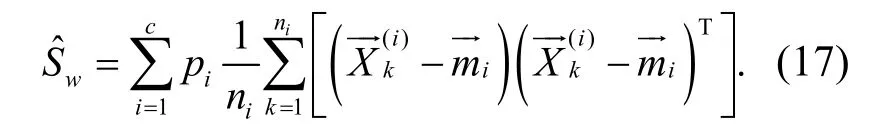
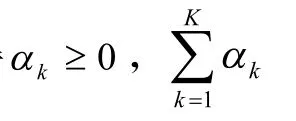
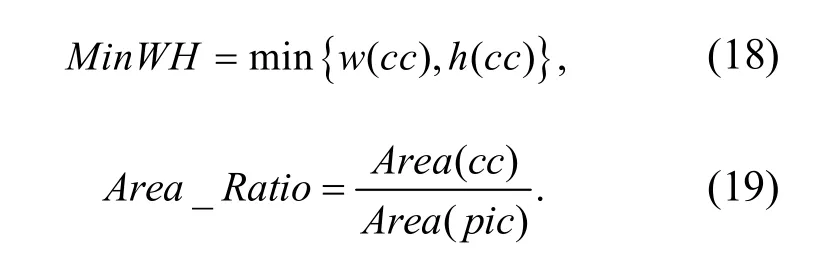
建立核函数，采用自适应加权控制方法进行粗糙集连续属性离散数据的信息熵特征提取，采用离散检验分析方法进行模糊聚类，可得到聚类中心表示为

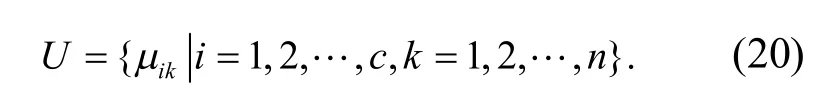
对粗糙集连续属性离散检验的调度函数为

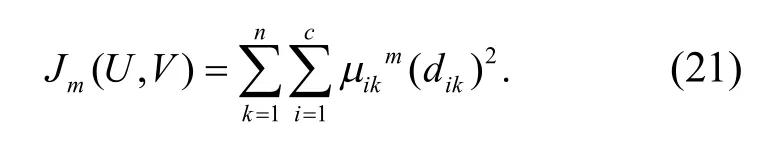
构建粗糙集连续属性离散数据集的特征匹配函数，在数据聚类中心，得到优化的粗糙集连续属性离散数据检验输出为

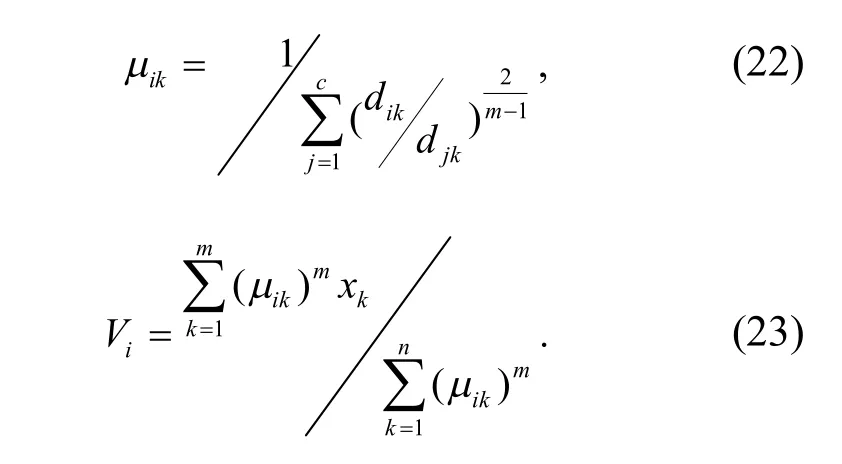
其中，m为粗糙集连续属性离散数据信息熵离散检验的适应度函数；(dik)2为样本xk与特征聚类中心与样本Vi的测度距离.

综上分析，根据粗糙集连续属性的融合结果，可以实现离散检验和数据挖掘.

3 仿真实验与结果分析

为了验证本文方法在实现粗糙集连续属性离散检验中的性能，进行软件仿真实验.采用Matlab 和C++进行算法设计，粗糙集连续属性的大数据采样样本为1 200，粗糙集连续属性离散数据采样样本个数为2 000，特征分布的权重系数为0.34，对粗糙集连续属性离散数据信息采样周期T=0.45 s，粗糙集属性信息干扰强度SNR=(-20～0) dB.根据上述仿真环境和参数设定，进行粗糙集连续属性离散数据检验，得到粗糙集连续属性离散数据的大数据集采样时域分布如图2 所示.

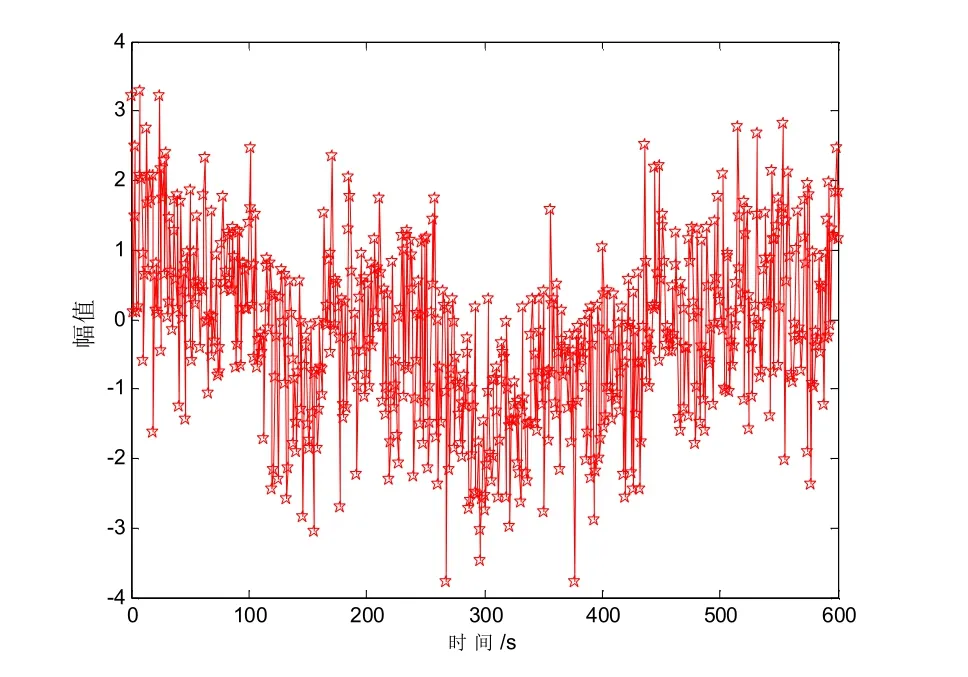
图2 粗糙集连续属性离散数据采样

以图2 的数据为研究对象，提取粗糙集连续属性离散数据的信息熵特征，结果如图3 所示.

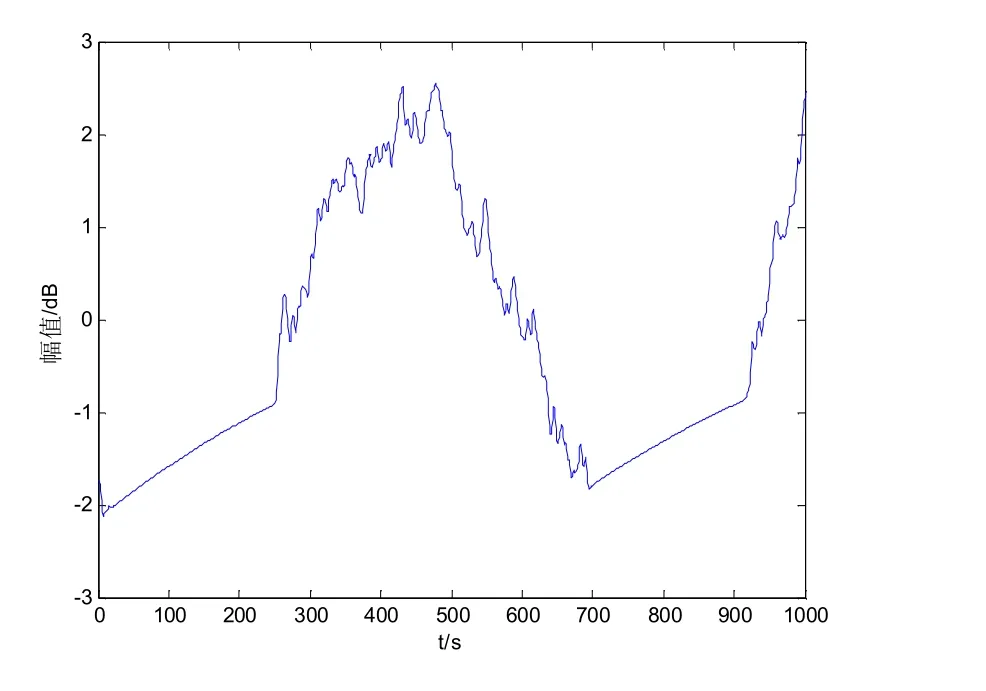
图3 粗糙集连续属性离散数据的信息熵特征

分析图3 得知，采用本文方法进行粗糙集连续属性离散数据特征提取的聚集性较好.测试不同方法下进行的粗糙集连续属性离散数据离散性检验，所得结果如图4 所示.

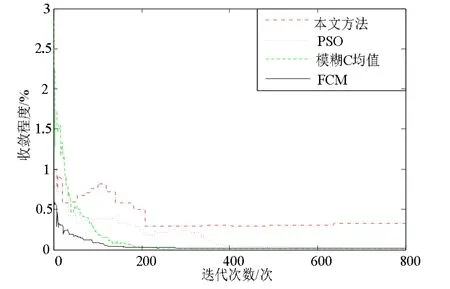
图4 不同方法下粗糙集连续属性离散数据检验

由图4 可知，按本文方法进行粗糙集连续属性离散数据信息熵离散检验的收敛能力较好.为进一步分析不同检验方法的收敛性，整理出实验数据结果如表1 所示.

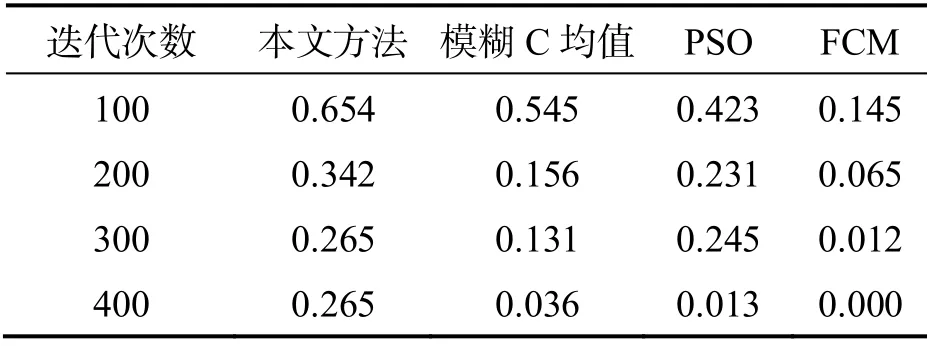
表1 不同检验方法的收敛度对比 %

根据表1 可知，随着迭代次数的增加，4 种方法的收敛程度均有所下降，但本文所提方法收敛程度最高；在迭代次数为400 时，本文方法离散检验的收敛程度为0.265%，远高于其它方法，证明本文方法进行粗糙集连续属性离散数据检验的误分类率较低，收敛性较好.

4 结语

通过提取粗糙集连续属性离散数据的信息熵，得到粗糙集连续属性离散数据所分布的序列特征，对其进行模糊聚类分析，获取离散数据闭繁项关联分析度量；再对粗糙集连续属性离散数据进行空间重组和信息融合，优化离散检验输出，以提高大数据粗糙集的分类融合和特征识别能力.仿真结果表明，采用本文方法进行粗糙集连续属性离散检验的数据聚类性较好，其收敛程度优于常见的3 种聚类算法，且在迭代次数为400 时，收敛程度仍高达0.265%.