解决高维INLP和MINLP问题的混沌差分进化算法

谭 跃，赵政春，杨 冰，肖 湘

(湖南城市学院 信息与电子工程学院，湖南 益阳 413000)

差分进化(Differential Evolution，DE)最初是由Storn 和Price 提出的，它是一种基于种群的随机搜索算法[1].目前，有许多方法被提出并用于改进其搜索能力，在这些方法中，混沌差分进化算法是一类非常有效的优化算法[2-4].

根据混沌的用途，常见混沌差分进化算法可分为2 类.第1 类是混沌全局搜索算法，它是用混沌序列来替换DE 算法中的一个或多个参数以增强DE 的全局搜索能力[5-8].之所以被称为混沌全局搜索算法，是因为DE 本身是一种全局搜索算法，用混沌序列替换参数没有改变它搜索的性质.第2 类是混沌局部搜索算法，它是在每一代的进化过程中，对当前种群的最优解叠加一个混沌序列来产生一组新解.由于这类算法都是基于最优解来搜索新解，因而它被认为是一种局部搜索算法.根据每次搜索过程中最优解向量维数改变的情况，混沌局部搜索算法又可分为单维的混沌局部搜索[9-10]和多维的混沌局部搜索[11-13].本文提出一种用于解决高维的整数非线性规划(INLP)问题和混合整数非线性(MINLP)规划问题的混沌差分进化算法，它是将上述2 类混沌差分进化算法融合在一起，再采用一种混沌全局搜索而构成的混合算法.

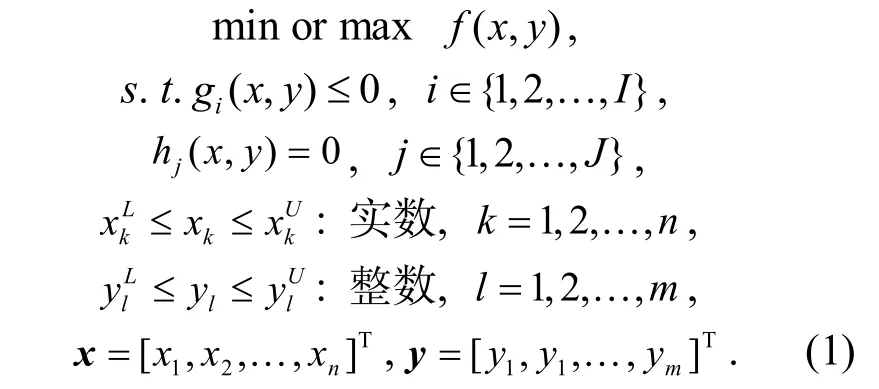
INLP 和MINLP 这2 类问题的目标函数以及 相应的约束条件通常都是由一些非线性的函数组成.INLP 问题决策变量的每一维都是整数，而MINLP 问题决策变量的有些维数为整数，其它的维数则为实数.与INLP 问题相比，MINLP 问题更难求解.一个MINLP 问题可以表示为 其中，max or min 表示最大最优化或最小最优化问题；x和y分别是n维的实数变量和m维的整数变量；f(x,y)为目标函数；gi(x,y)和h j(x,y)分别是不等式和等式约束条件；和分别是第k维实数变量的下界和第l维整数变量的下界，和是其对应的上界.

求解INLP 和MINLP 问题可以分为确定性算法和启发式算法.确定性算法又包括分支定界算法[14]、扩展切平面算法[15]和外逼近算法[16]等.启发式算法，特别是那些基于种群的元启发式算法如差分进化[17]、粒子群优化算法[18]和遗传算法[19]等深受很多学者的青睐.

1 一种新的混沌差分进化算法

大多数学者只用了第1 类或第2 类混沌差分进化算法来求解某个或某类具体的优化问题.实际上，第1 类混沌差分进化算法能较好地提高DE的全局搜索能力，因为DE 是一种随机的全局搜索算法；第2 类混沌差分进化算法则能较好地提高DE 的局部搜索能力，因为每次搜索时只基于当前种群的最优解在一个小的搜索范围内产生一个新解.根据上述2 类混沌差分进化算法的特点可知，一个好的混沌差分进化算法应能同时提高DE的全局和局部搜索能力.

1.1 混沌序列替换DE 的参数

差分进化算法包含变异、交叉和选择这3 种操作，变异操作[1]表示为

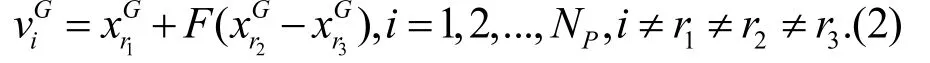
当DE 求解高维的INLP 和MINLP 问题时，让缩放因子F保持固定不变的常数能导致种群的多样性不足，因而降低DE 的全局搜索能力.为解决这一问题，可用一个变化的参数来替换缩放因子，所以采用混沌序列来实现这一目的.尽管有许多动态系统具有混沌行为，但是Logistic 映射是应用最广的一种混沌系统，它被定义为

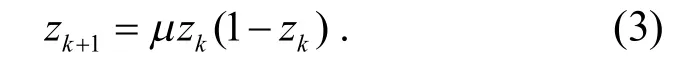
其中，k为迭代次数；μ是控制参数.当μ= 4，z( 1) ∈ (0,1)且z(1) ≠ {0.25,0.5,0.75}时，式(3)表现出混沌行为.将式(3)zk+1替换式(2)的F时，则变异操作为

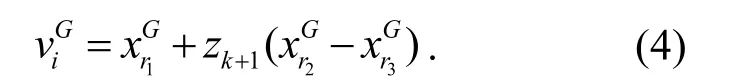
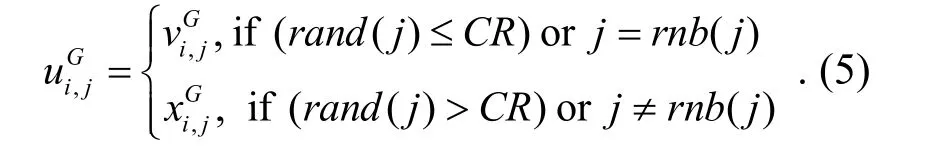
其中，交叉因子CR可以在(0,1)的范围内变化；j∈ {1,2,...,D}中D是求解问题的维数；rand(j)是在(0,1)范围产生的一个均匀分布随机数；rnb(j)是[1,D]的一个随机整数.

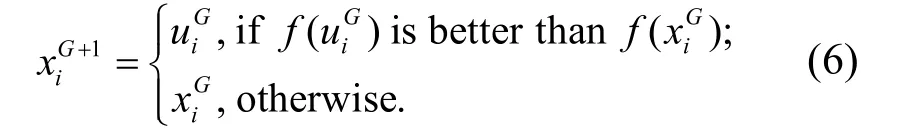
其中，f为目标函数；为第G+1 代的第i个个体.

1.2 混沌局部搜索

在元启发式算法中通常是当前种群的最优解用于局部搜索.根据每次搜索时最优解向量维数改变的情况，混沌局部搜索可以进一步分为单维和多维的混沌局部搜索.单维混沌局部搜索每次搜索时只有最优解向量的某一维被改变，这种搜索方式实际上是一种精细搜索；多维混沌局部搜索在每次搜索时最优解向量的每一维都会发生改变，与单维混沌局部搜索相比，它能执行范围更大的局部搜索.一个同时具有单维和多维搜索能力的混沌局部搜索算法可以描述为

其中，rand是一个(0,1)范围的随机数，且rand≠ {0.25,0.5,0.75}；ML为总的混沌局部搜索次数；D表示求解问题的维数.式(7)中pi,j表示第i次多维混沌局部搜索产生的解向量的第j维；b sj为当前种群最优解向量bs的第j维；α是一个控制多维混沌局部搜索步长的参数；而randint(1,D)表示在[1,D]产生的一个随机整数D.式(8)中pi,r表示第i次单维混沌局部搜索产生的解向量的第r维；参数β用于控制单维混沌局部搜索的步长.式(9)中f是目标函数；a表示混沌局部搜索产生的所有解向量，即p1,p2, …,pk, …,pML中的最大目标函数值.式(10)中pb表示p1,p2, …,pk, …,pML中的最优解.

1.3 混沌全局搜索

在元启发式算法中混沌映射的2 个主要应用是替换参数和混沌局部搜索.实际上，混沌映射还可以用来执行全局搜索.当每次进行混沌全局搜索时，通过混沌映射方程在整个解空间产生一个新解.在所有的新解产生之后，再从其中选择出最好的解与当前种群的最优进行比较，如果前者优于后者，则后者被前者替换.混沌全局搜索描述如下：

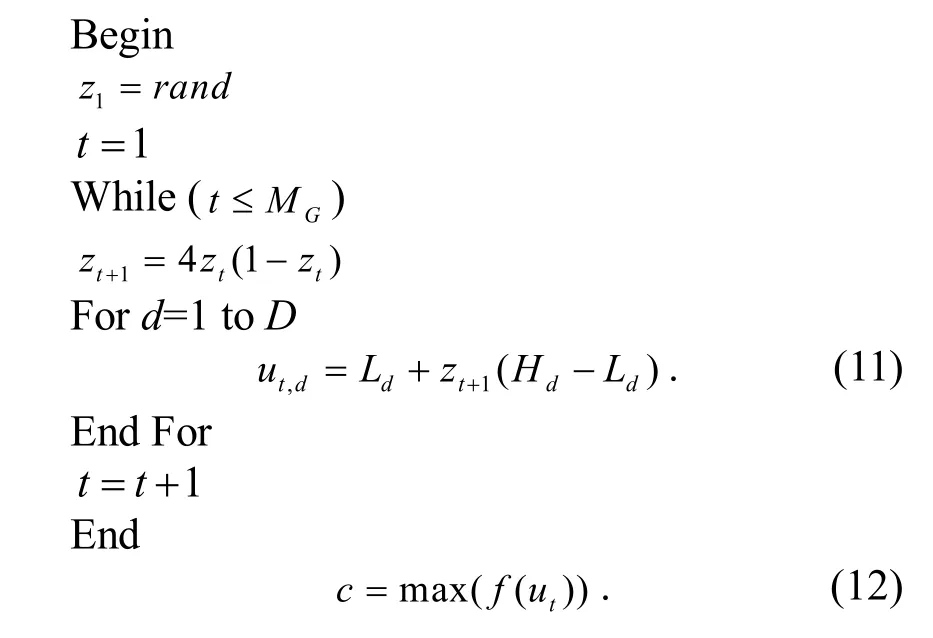
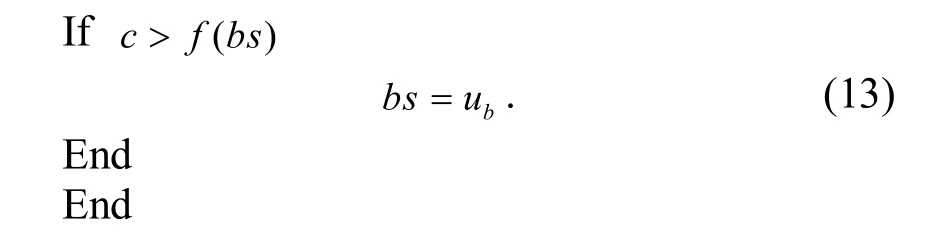
其中，rand是一个(0,1)范围的随机数，且rand≠ {0.25,0.5,0.75}；t是迭代次数；MG是总的混 沌全局搜 索次数. 在式(11) 中，ut,d(d= 1,2,...,D，D是求解问题的维数)是第t次混沌全局搜索产生的新解的第d维；Ld和Hd表示相应的决策变量第d维的下界和上界.式(12)中f表示目标函数；c是混沌全局搜索产生的所有解向量u1,u2,...,uMG的目标函数最大值.在式(13)中ub表示u1,u2,...,uMG中的最优解.

1.4 算法步骤

所提出混沌差分进化算法(简称为CGLSDE)的步骤如下：

1)初始化种群大小PN，交叉因子CR，最大进化代数 maxG，所有决策变量的上界和下界，总的混沌局部搜索次数LM，总的混沌全局搜索次数GM.

2)根据式(14)和式(15)产生包含n维实数和m维整数的一个个体，若该个体不满足所有的约束条件，则重复这一过程直到产生PN个满足所有约束条件的个体作为初始种群.

其中，η表示在(0,1)的一个均匀分布随机数；和是相应的决策变量下界，和是对应上界；randint()为和间一个随机整数.

3)对PN个初始个体进行评价，选出目标函数值最好的个体作为当前种群的最优解bs，设进化代数 1g= .

4)根据式(3)和式(4)执行变异操作.

5)通过式(5)执行交叉操作.

6)根据式(6)进行选择操作，若选择操作后的个体优于bs，则用前者替换后者.

7)执行1.3 节中的混沌全局搜索后再执行1.2节的混沌局部搜索.

8)g←g+ 1，若g≤Gmax，则转步骤4，否则输出结果并结束程序.

1.5 约束条件的处理

当元启发式算法应用于求解INLP 和MINLP问题时，通常需要对这些问题的约束条件进行处理.处理约束条件最简单的方法是保留可行解而舍弃不可行解，这里也采用这种简单策略来处理约束条件.在CGLSDE 算法中，当执行变异、交叉、混沌局部搜索和混沌全局搜索时，若有n维实数和m维整数的一个解变成了另一个(n+m)维的实数解时，则将该解中相应的m维实数通过四舍五入变为m维整数.若通过四舍五入变化之后的解不满足所有约束条件，则将其舍弃.

2 仿真实验及分析

2.1 测试问题

4 种算法，即本文提出的CGLSDE、文献[5]中的 CDE、文献[10]中的 DEMSCLS 以及CLSDE(文献[13]中提出的混沌局部搜索与本文1.1 节中差分进化算法相结合的一种混合算法)被用于求解4 个高维的测试问题.

1)问题P1.P1 属于高维的INLP 问题，其目标函数及约束条件如下：

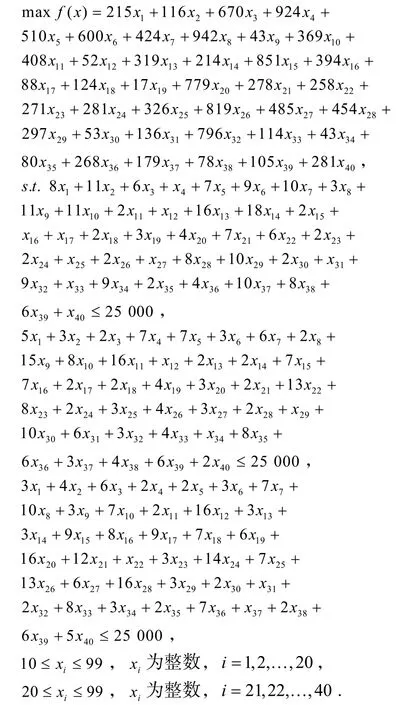
P1 的全局最优解为

对应的目标函数最大值fmax(x) = 1 352 439.

2)问题P2.P2 是一个高维MINLP 问题，其目标函数和约束条件函数与问题P1 完全相同，但其决策变量中的20 维为整数，20 维为实数，具体如下：

3)问题P3.P3 也是一个高维的INLP 问题，其目标函数及约束条件如下：

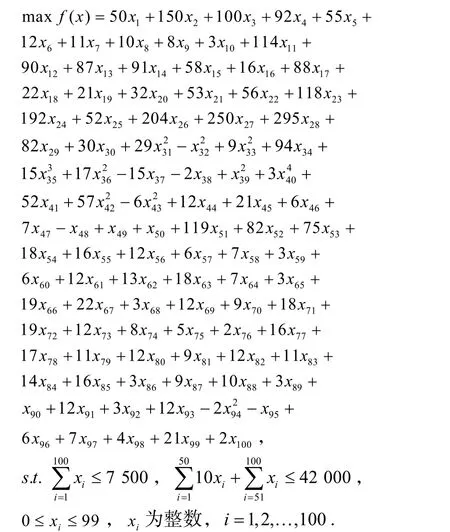
已知的最优解由CLPSO 算法获得[20]，对应的目标函数最大值fmax(x) = 304 117 194.

4)问题 P4.该测试问题是一个高维的MINLP 问题，目标函数和约束条件函数与P3 相同，但其决策变量中的50 维为整数，50 维为实数，具体如下：

2.2 实验结果及分析

CGLSDE 算法参数设置如下：种群大小PN为问题维数的3 倍；交叉因子CR为0.5；最大进化代数 maxG为400 代；总的混沌全局搜索次数GM和混沌局部搜索次数ML分别为NP/6和NP/3；当对当前最优解向量的m维整数进行混沌搜索时，参数α为区间[-5,5]的一个随机整数；若对n维实数进行混沌搜索时，α为( - 1)i，其中i为当前的搜索次数；类似地，控制参数β设置为[ -2 ,2]的随机整数或0.1( - 1)i；为公平起见，DEMSCLS 算法中总的混沌局部搜索次数为NP/2.

每个问题用上述4 种算法求解50 次，所得到的结果如表1 所示.

由表1 可知，对于P1，CGLSDE 每次都能找到全局最优值，CDE 和CLSDE 有时能找到，但DEMSCLS 都不能找到；当优化P2 时，CGLSDE优于其它3 种算法，而CDE 和CLSDE 优于DEMSCLS；对于P3，CGLSDE 获得的结果都好于CDE、CLSDE 和DEMSCLS，而CDE 获得的每个结果都比CLSDE 和DEMSCLS 差；当优化P4 时，CGLSDE 获得的结果最好，DEMSCLS 次之，CLSDE 最差.总之，CGLSDE 在优化上述4个问题时获得的结果整体都好于CDE、CLSDE和DEMSCLS.

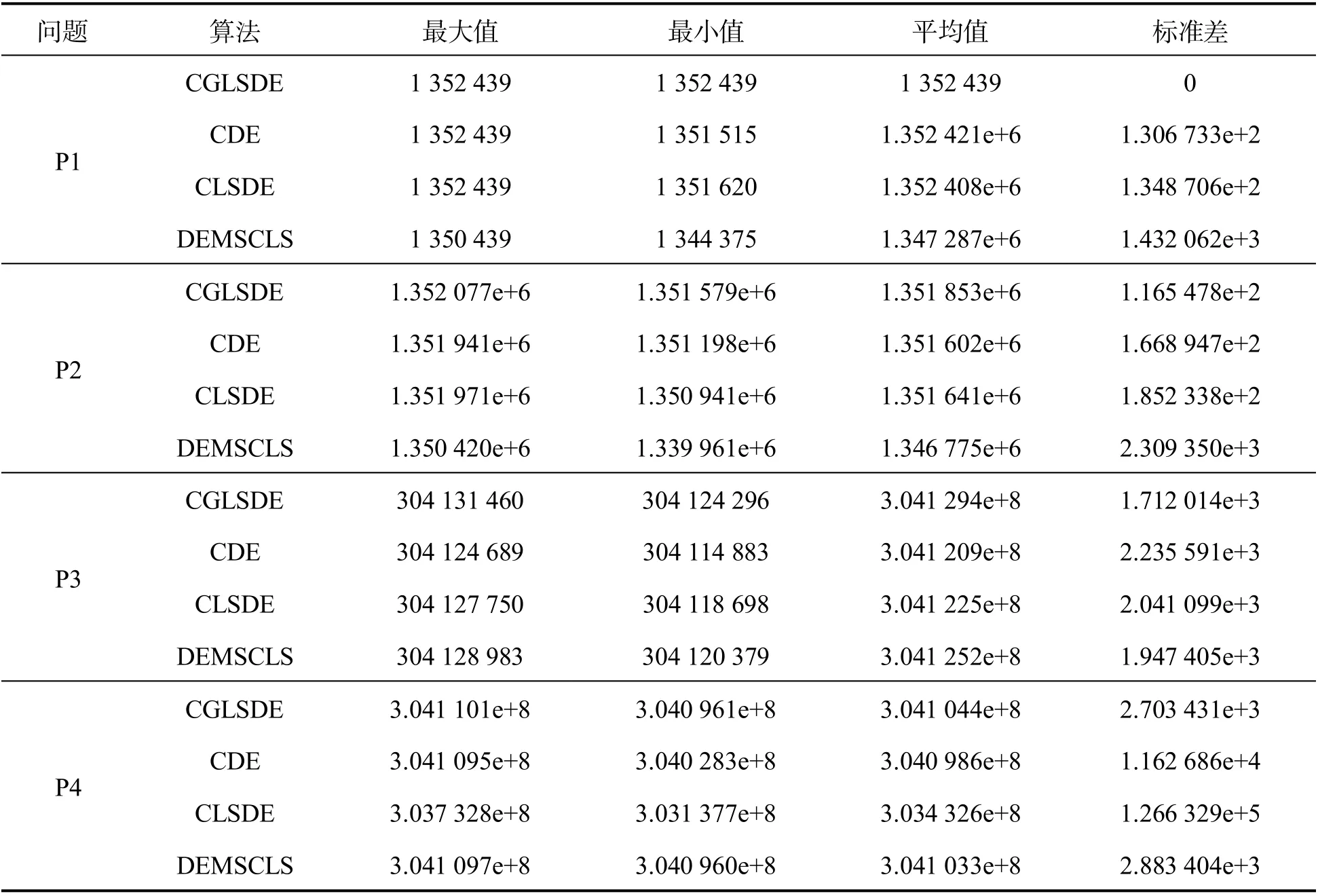
表1 4 种算法分别对P1～P4 单独优化50 次的结果

为了对不同算法的平均收敛速度进行直观地对比，对4 个函数50 次实验的每一代最优个体目标函数值的平均值进行计算，所得到的结果分别如图1～图4 所示.

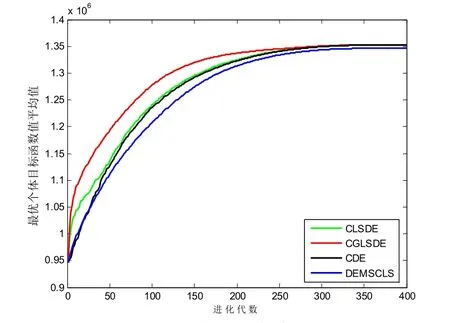
图1 P1 的平均收敛速度

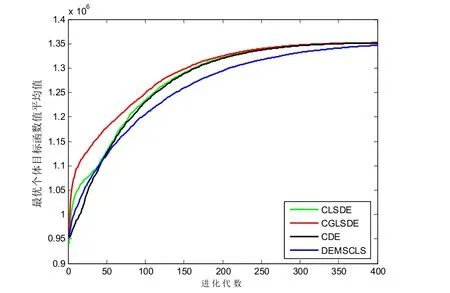
图2 P2 的平均收敛速度

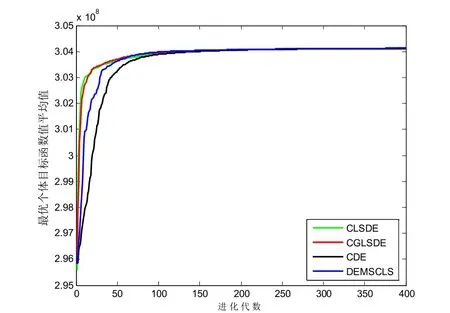
图3 P3 的平均收敛速度

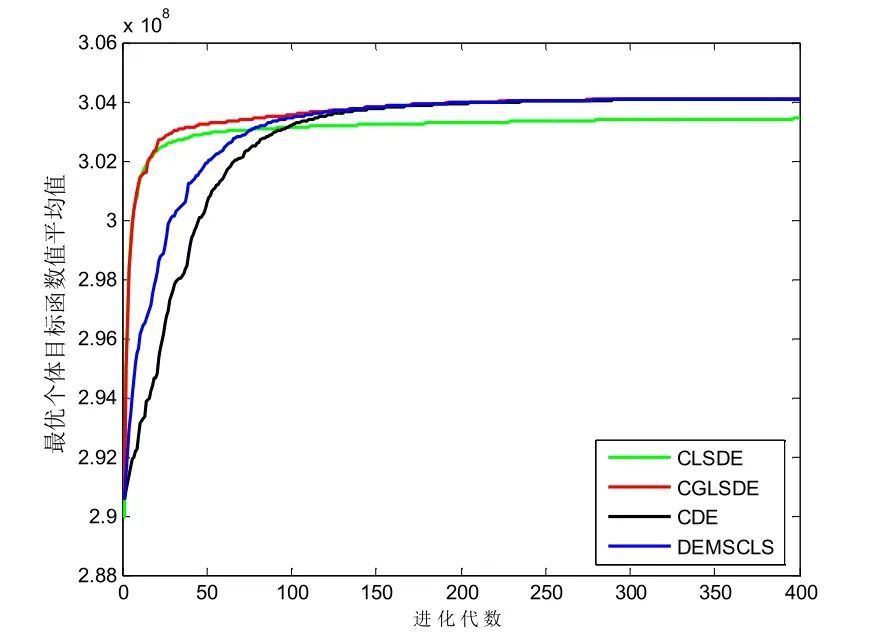
图4 P4 的平均收敛速度

从图1～图4 的平均收敛速度曲线对比中不难发现，CGLSDE 平均的收敛速度是4 种算法中速度最快的.根据以上比较可看出，CGLSDE 优于CDE、CLSDE 和DEMSCLS.在4 种算法中，CDE只用混沌序列来替换DE 的参数，CLSDE 和DEMSCLS 都能对当前种群的最优解执行多维的混沌局部搜索，而DEMSCLS 还具有单维的混沌局部搜索能力.从本质上来说，CGLSDE 可以视为在CDE 和DEMSCLS 结合的基础上再通过混沌全局搜索来进一步增强DE 全局搜索能力.因此，CGLSDE 比CDE 和CLSDE 具有更强的局部和全局搜索能力，而比DEMSCLS 具有更强的全局搜索能力.

3 结束语

为了同时改进DE 算法的局部和全局搜索能力，提出了一种被称之为CGLSDE 的混沌差分进化算法.该算法采用了单维和多维的混沌局部搜索改进其局部搜索能力，还利用混沌序列替换缩放因子并采用混沌全局搜索方式来改进其全局搜索能力.对CGLSDE 与其它3 种混沌差分进化算法(CDE、CLSDE 和DEMSCLS)用于解决4 个高维的INLP 和MINLP 问题进行了比较，仿真结果表明CGLSDE 要优于其它3 种算法.