双Boost无桥PFC变换器无差拍控制算法
文/蔡碧贞
功率因数校正(Power factor correction,PFC)是一种有效抑制谐波的方法。如今在一些大大小小的电子产品中都必须要添加PFC功能,目的是为了抑制电子产品的谐波对电网安全性产生影响。随着高功率、高密度电子设备不断深入研究,传统桥式PFC变换器因损耗高、电流THD偏大等缺陷凸显了其局限性。双Boost无桥PFC变换器因减少了整流桥和一些功率器件,能大大减小损耗,同时变换器输入电流不易断续,在功率因数校正场合得到广泛使用。
双Boost无桥PFC是实现PFC比较常用的一种拓扑,实现PFC的算法很多种,比较常用的如预测控制,无差拍控制,PI控制等。为了实现高功率密度,拓扑的体积需要作出限制,一些磁性元器件如电感、变压器等占据系统绝大部分体积的器件就需要限制大小。当电感变小时,双Boost无桥PFC在轻载下,电感电流会变成断续模式(DCM)。当参数模式发生变化时,传统的双环控制就无法兼顾两个模式下的控制精度。假设在CCM模式下,系统处于轻载时控制就会出现问题,电感电流会发生很大的畸变。为了解决这个问题,本文特地对双环无差拍控制算法添加了前馈补偿来解决轻载控制造成的电流畸变问题。
1 双Boost无桥PFC变换器建模分析
模态1:输入电源处于正半周,此时MOS管S1导通,L1充电储能,电感电流逐渐增大,回路由L1、S1和D3组成,输出端由Co供电,等效电路图如图1(a)所示。电感电流的增量为:
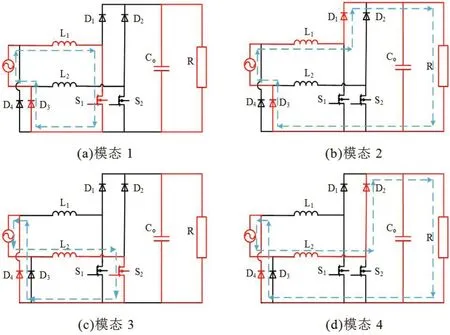
图1:双Boost无桥PFC工作模态分析

图2:无差拍控制框图
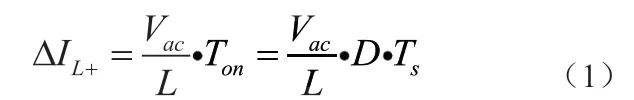
模态2:输入电源处于正半周,此时MOS管S1关闭,输入源以及L1对输出端放电,同时对Co进行充电,电感电流减少,回路由L1、D1、R和D3组成,等效电路图如图1(b)所示。电感电流的减量为:
模态3:输入电源处于负半周,此时MOS管S2导通,L2充电储能,电感电流逐渐增大,回路由L2、S2和D4组成,输出端由Co为负载供电,等效电路图如图1(c)所示。电感电流增量与模态1相同。
模态4:输入源处于负半周,此时MOS管S2关闭,输入源以及L2对负载端放电,同时对Co进行充电,电感电流减少,回路由L2、D2、R和D3组成,等效电路图如图1(d)所示。电感电流的减量与模态2相同。
2 无差拍控制算法研究
参照图1,S为开关管状态,可由式(1)表示,1表示导通状态,0表示截止状态,分别对应开关管导通和关断两种模态。
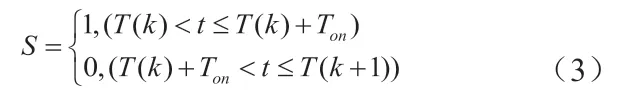
取IL和Vo为状态变量,当开关管导通时,其状态方程为:
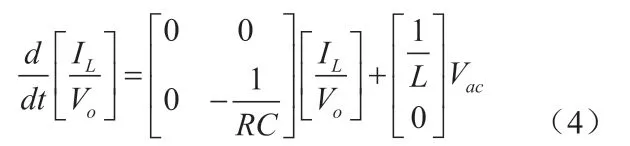
当开关管关断时,其状态方程为:
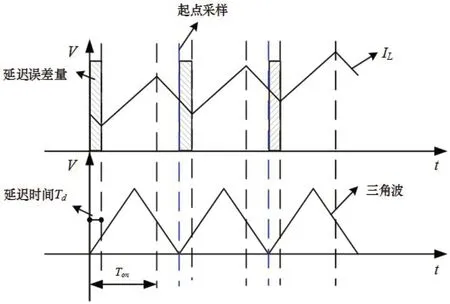
图3:改进前无差拍控制示意图

图4:改进后无差拍控制示意图
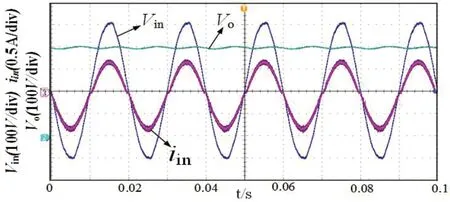
图5:满载下输入输出波形
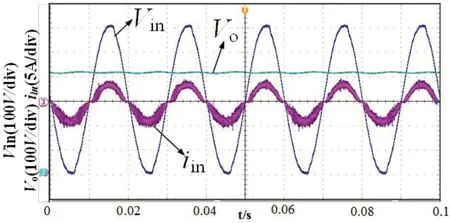
图6:半载下输入输出波形

图7:100W轻载电流波形

对上述两式取时间平均得:
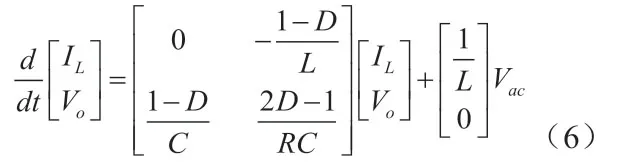
其中Vac指输入电压,IL指电感电流,Vo指输出电压,D为占空比,r指线上回路等效电阻(这里取r为0)。
又因为电感电压为:

离散化后可知单相整流的离散状态方程可表示为:
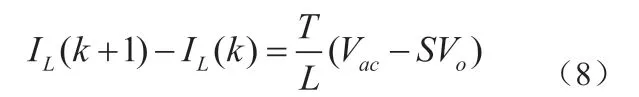
假设系统实现无差拍控制,即采样值IL(k+1)完全跟随参考值IL*(k+1),则离散后输入电流状态方程可表示为:
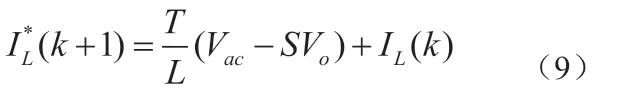
设系统一个开关周期从kTs开始,载波采用三角波,忽略线上回路电阻,则单个周期内输入电流变化公式为:
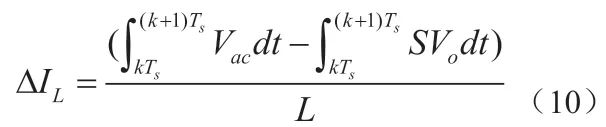
单个周期内电感电流的增量为:
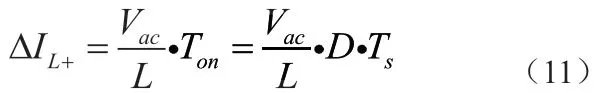
单个周期内电感电流的减量为:
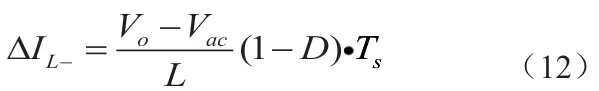
单周期内的电感电流变换量为:

那么,下个周期的电感电流可表示为:

其中D为占空比。
当开关频率足够高时,在单个开关周期内可将Vo值视为恒定,由公式(11),(12),(13),(14)得占空比的表达式:

2.1 前馈补偿研究
从式(15)可以看出基于双Boos无桥PFC变换器推导出的无差拍占空比表达式由两部分构成,一部分为电流项,电流项在公式中占据很小的比重,是调节电流跟踪精度的关键成分,属于动态项;另一部分为电压项,电压项属于稳态项,在式中占据很大比重。公式(15)是基于电感电流连续模式推导得到,当系统工作在DCM模式时,模式发生很大的变化,因为电压项占据很大比重,如果不对其做修改,会造成输出电压不稳定以及电感电流畸变。为此特地对电压稳态项做前馈补偿来弥补这个问题。
在CCM模式,电压项可表示为:

那么CCM模式下,电压项占空比可表示为:

同样在DCM模式下,电压项的表达式可表示为:
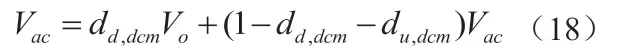
断续模式下电感电流可表示为:

而单个周期内开关导通时:

由公式(19)、(20)可得:

将式(21)代入式(18)中可知,DCM模式下电压项占空比表达式为:

其中df,ccm和df,dcm分别表示CCM模式、DCM模式下电压项占空比,du,dcm表示DCM模式下电感上升到峰值的电压项占空比,dd,dcm表示DCM模式下电感电流下降到零的电压项占空比。当式(22)取最小值时,就是系统的CCM模式,在电感处于CCM模式下df,dcm>df,ccm,当电感处于DCM模式时,df,dcm 数字延迟现象如图3所示,为了解决数字延迟现象对控制的干扰,本文对无差拍控制算法作了改进处理。本文在开关周期中点采样进行计算,在下个开关周期时刻一到即输出所得控制信号。已知上个周期三角载波右半部分的导通时间,可得出下个周期三角载波左半部分的导通时间,通过计算三角载波左右导通时间的总和来实现无差拍控制,从而克服了采样和计算延迟现象。改进算法解决了DSP固有的一个周期延迟现象。 改进后的无差拍控制示意图如图4所示。将采样点放在周期中点,改进算法留有半个周期时间可供采样和计算,当下一周期时刻一到立即输出控制信号。因而改进型无差拍控制会出现三角载波左右导通时间不对称的特点。 周期中点采样得到表达式为: 改进型算法的实际开关周期为相邻采样值的区间大小。如图4所示,系统在三角载波左半部分导通时间为: 右半部分导通时间为: 系统在一个开关周期的导通时间总和为: 其中PRD表示三角载波周期。 改进型无差拍控制占空比可表示为: 为了验证本文提出的控制方法的有效性,研制了一台1KW的实验样机。实验中数字控制芯片采用TMS320F28377D,设计开关频率fs=50KHz,S1、S2选用SPW24N60C3,二极管D1~D4选用STTH1212D。 图5、图6分别为1000W和500W功率下的相关波形。对满载时输出电流进行FFT分析,可得其THD为3.58%,PF值为0.9979,电流波形平滑,跟踪效果好。在500W下电感电流也能跟踪上输入电压,但是电流过零点的畸变比较明显。对波形进行FFT分析,得到半载下输出电流THD为10.17%,PF值为0.9875。这是因为双环控制中外环PI和内环无差拍的动态响应不同步,外环PI的积分环节导致系统动态响应比较缓慢。这种现象随着功率变化而发生变化,特别是在较低的功率下,因响应速度较慢会导致系统产生严重的过零点畸变现象。 轻载(100W)情况下如果未添加稳态前馈补偿,波形如图7(a)所示,特别在电流峰值附近,电流畸变严重,此时电感电流处于断续模式,这会对电网电流波形产生较大的谐波干扰;在添加了稳态前馈补偿后,波形如图7(b)所示,电流失真得到改善。 双Boost无桥PFC在轻载下,电感电流会变成断续模式,产生很大电流畸变,导致系统PF降低。本文从双Boost的建模分析推导了无差拍的表达式,从理论上解释了由于在轻载下,无差拍控制前馈部分发生变化,导致控制效果不好的原因,通过添加稳态前馈补偿来弥补无差拍控制带来的影响;同时针对数字采样延迟,对无差拍算法做改进处理,以改善电流跟踪效果,提高系统PF值。最后,研制了一台1KW的实验样机,实验结果验证了相关分析的正确性和所提出的控制策略的有效性。2.2 数字延迟现象处理


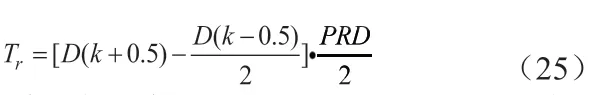
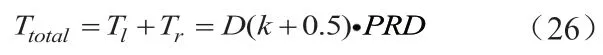

3 实验验证
4 结论

