基于Matlab的配网带电作业机器人正逆运动学仿真
文/李帅 张金禄 么军 李威 何玉龙
1 引言
电力工业是国民经济的基础,配电网又是其关键环节。当线路发生突发故障时,停电检修对社会经济影响巨大,严重影响百姓日常生活;另外,停电以及检修完毕之后的上电都会对系统内的设备造成冲击伤害,影响设备的使用寿命。传统意义上的带电作业,作业人员通过绝缘作业工具与带电设备接触,检修作业强度大,危险性高,人员受伤情况难以避免。
因此,通过研发一种配网带电作业机器人,不仅可减少作业时间即停电时间,同时还可以提高作业的可靠性,保护带电作业人员,就显得尤为重要。
2 机器人D-H法
Denavit-Hartenbery法简称D-H法。该方法于1956年由上述两位学者提出,绝大多数机械臂的数学模型可由该方法构建。绝大部分的关节型机械手臂,按顺序将转动副和移动副固定在连杆上,连杆不在同一平面,并且旋转轴彼此不平行。连杆坐标建立方式如图1所示。
Ci-1、Ci、Ci+1三个不同连杆对应各自关节i-1,i,i+1,Ji、Ji+1为关节i和i+1的轴线,作其公垂线与对应坐标系OiXiYiZi中的Ji+1交点为坐标原点,Zi轴与Ji+1轴平行且向上,Xi轴平行于公垂线,远离Ji轴为正方向。Ji对应坐标系Oi-1Xi-1Yi-1Zi-1。
参数aiαiθidi各自代表不同含义,在单个连杆关节中包括两个参数连杆长度ai表示单连杆长度,即公垂线上Ji、Ji+1间距离。αi表示Zi与Zi+1之间的偏转角度,逆时针为正。Di表示相邻两个连杆公垂线间距离。θi表示相邻两个连杆之间的扭转角,逆时针为正。
在连杆坐标系中,相邻两连杆可通过平移与旋转互相转换,分为以下四步:
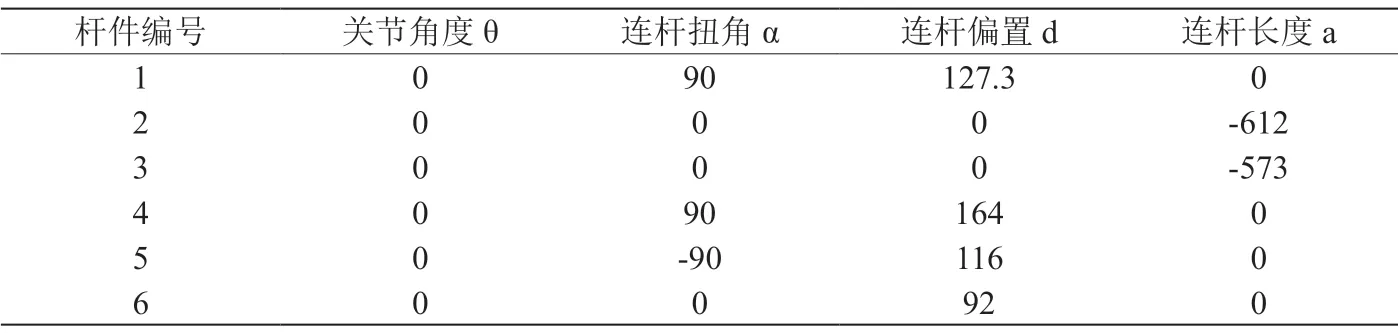
表1:机械臂连杆D-H参数

图1:连杆坐标建立方式
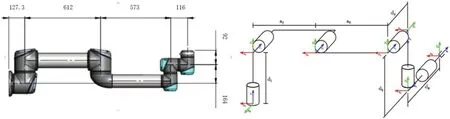
图2:配网带电作业机器人机械臂模型
(1)将初始连杆绕坐标系Z轴旋转,旋转角度为θ,使初始连杆与目标连杆的X轴共面;
(2)将初始连杆绕坐标系Z轴平移,平移距离为d,使初始连杆与目标连杆的X轴共线;
(3)将初始连杆绕坐标系X轴平移,平移角度为a,使得初始连杆与目标连杆坐标原点重合;
(4)将初始连杆绕坐标系X轴转动,转动角度为α,使得初始连杆与目标连杆Z轴共线;
将连杆坐标转换通过矩阵定义如下:

坐标系变换:
机器人运动求解过程中,机械臂末端的位姿可以通过连杆的坐标系变换得到。机械臂数学模型的建立关键在于找到局部坐标系在全局坐标系中的映射关系。发生平移时,其变换矩阵为Tr(dx, dy, dz):

旋转角度为θ的坐标系3个方向的变换矩阵分别为:

令PU表示点P相对于坐标系U的描述;TUR表示坐标系R与U之间的变换矩阵;即点P与坐标系R之间的转换关系如下PR:

图3:配电机器人机械臂起始状态

图4:机器人运动学仿真界面

图5:运动学正解
PR=PU×TUR
3 机器人数学模型建立
3.1 机械臂数学模型
为了完成机器人的仿真,第一步是创建其数学模型。Robotics工具箱的Link可用于构建其模型。
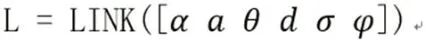
其各个参数定义如下:
(1)a为连杆长度,Z轴在X轴上的偏移;
(2)α为连杆扭角,Z轴绕X轴转角,逆时针为正;
(3)d为连杆偏置,X轴在Z轴上的偏移;
(4)θ为关节角度,X轴绕Z轴转角,逆时针为正;
(5)σ代表关节类型:0表示旋转关节,1表示移动关节;
(6)φ代表移动关节偏移量。
本文所用机械臂如图2所示。该机械手由六个旋转关节组成。各杆件的D-H参数如表1所示。
3.2 机器人正运动求解
正运动求解,即把关节变量、机器人末端初始位姿、各关节变化角度当作已知,把机器人末端的最终位姿当作未知的求解过程。表示为连杆i相对于连杆i-1的坐标位置。的变换通式为:
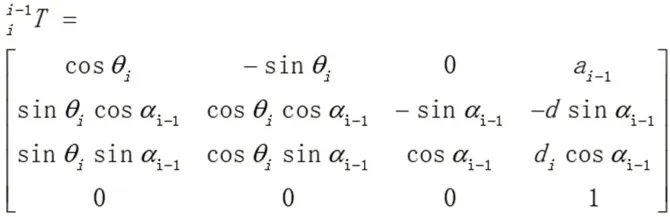
本文机器人机械臂末端位姿可表示为:

3.3 机器人逆运动求解
逆运动求解,即把关节变量、机器人末端初始位姿、最终位姿当作已知,把关节变化角度当作未知并求解的过程。逆运动问题实际上是运动方程的解。
给定末端执行器的位姿,即已知n,o,a,p的坐标。对于每个变量,只需将所对应的连杆进行逆变换,即可求解θ1, θ2, θ3, θ4, θ5, θ6。
变量公式分别如下:

3.4 初始状态仿真
在本文作业任务中,需两条机械臂相互协调配合,方可完成接引流线任务,两机械臂初始状态角θ分别为[90° 100° -50° 30° -90° 0]和[90° 70° 30°-20° -90° 0]。结果如图3所示。
3.5 仿真界面设计
对双臂数学模型的运动学和动力学仿真,其实质为每一条壁单独仿真,出于模拟工况较多的考虑,需进行大量重复编写或更改代码,每一次修改都在源代码里修改,容易出现疏漏,不够直观,且造成模拟效率的下降,将程序模块化,整合为如图4所示界面。
仿真界面左侧为模型建立部分,首先输入连杆的各个参数,包含关节角度θ,连杆扭角α,连杆偏置d,连杆长度a,连杆的初始长度和变化范围。为简化输入步骤,设置了默认参数一键输入功能。待各连杆参数确定后,点击建立模型,后台程序即可生成数学模型,并可通过绘图和动态演示可视化模型状态。
仿真界面右侧为运动学分析部分,可输入各连杆的初始位置、正求解位置和逆求解位置。为简化输入,设置了默认参数一键输入功能。待各连杆初始和终止位置确定后,点击正求解,即可在下方正解位置矩阵处显示结果,并可通过绘制轨迹曲线可视化模型位置。反求解环节亦同上。
4 机械手臂运动学仿真
正运动学问题(DKP)和逆运动学问题(IKP)是机械臂运动学仿真中的主要问题。
4.1 正运动学问题仿真
调用MATLAB中Robotics工具箱对机械臂数学模型正运动求解过程如下:
T=fkine(robot,q);
Robot为所建立的机械臂数学模型,q为关节变化角度,T为多得正运动求解。选取左侧机械臂为例,数学模型的各关节初始状态设为q0,各坐标变化量为qz,其正运动学求解过程为:

运行后,由MATLAB计算得到的运动学正解如图5,其中最后一列为机械臂末端位置坐标(-164.0000 -631.4900 26.9651),正解模型如图6。用jtraj函数仿真其1秒运动轨迹,如图7所示。
4.2 逆运动学问题仿真
调用MATLAB中Robotics工具箱对机械臂数学模型逆运动求解过程如下:
q=ikine(robot, T, q0, m)
其中,q是逆运动学问题的解,即每个关节的变化,robot是机械手的数学模型,q0是关节初始角,T为反求解的变换矩阵,m是4×4矩阵。
T1是正运动解的结果。逆运动求解过程如下:
qz2=ikine(bot, T1, q0, m)
运行后,由MATLAB计算得到的运动学逆解为:
qz2=[1.0749-2.2721 -1.7441 -0.5394 1.6551 -0.4807]
与qz1不同,将逆解qz2带入正求解方程,得末端位置坐标[-164.0000 -631.4901 26.9652]与正问题求解工程中给定的末端位置坐标相同,即证明相同位置坐标可通过不同坐标变换得到,同时也证明逆运动求解的不唯一性。
5 结论
使用D-H方法,建立了用于配电网带电作业的机械臂的结构参数,并在MATLAB Robotics工具箱中建立了其模型,完成了机械臂正逆问题的求解和仿真,并完成其轨迹规划,
为日后作业过程中可能遇到不同复杂工况下的轨迹规划、离线编程和动态设计等研究奠定了基础。
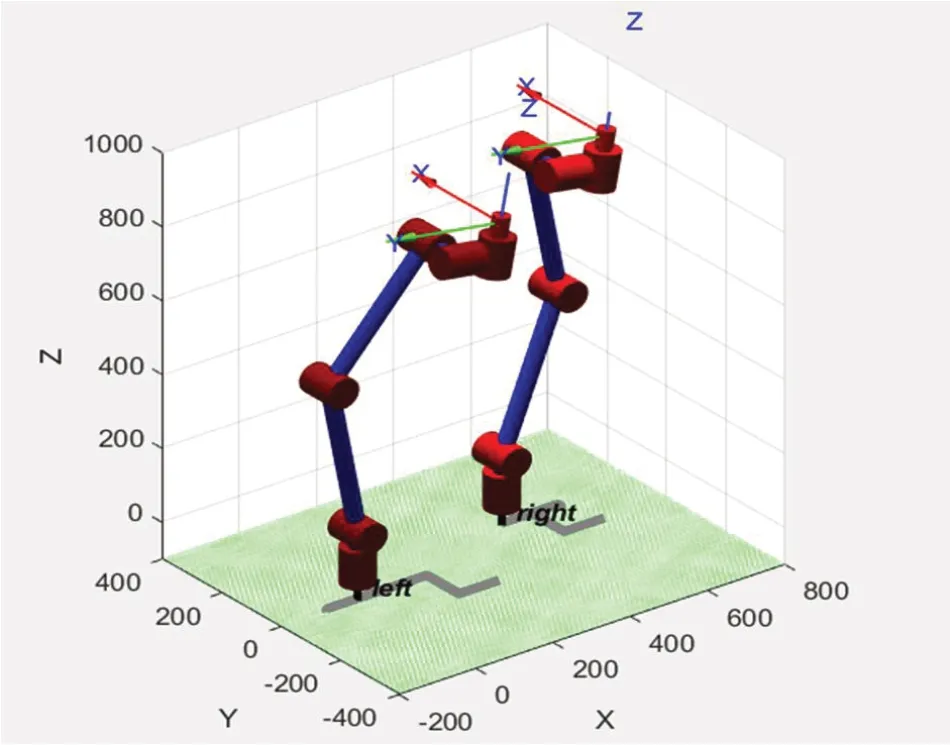
图6:运动学正解模型
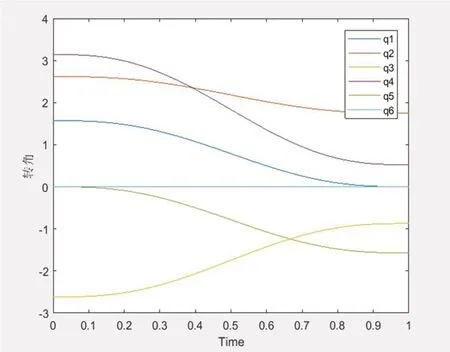
图7:正求解各关节运动过程

