基于多重分形谱的木材高光谱图像纹理分类算法
唐艳慧,赵 鹏,王承琨
(东北林业大学 信息与计算机工程学院,黑龙江 哈尔滨 150040)
1 引 言
精准快速地对木材进行分类在工业生产中具有重大意义。使用计算机智能手段对木材进行分类不仅可以减少工作人员的工作量,同时也可以弥补经验和技术的不足减少木材分类出错率。目前使用计算机手段对木材分类的研究主要集中在数字图像处理上。
目前木材树种分类识别主要可以分为宏观和微观两种分类方法,利用宏观方法对木材树种进行分类主要是指使用木材表面的纹理结构、木材的颜色等特征标记木材种类。但是由于木材生长环境复杂极易造成颜色、纹理等特征被篡改或破坏,使得木材错分率增加。另一种方法是使用木材的微观结构对木材树种进行识别分类,该类方法具有极高的分类正确率。近几年来,许多学者利用木材的微观纹理结构对木材进行分类并取得可喜的科研成果。印度学者Yadava[1-2]等人利用DWT变换和LBP(局部二值变换)对木材的微观数字图像进行了识别,正确率均在90%以上。希腊学者Barmpoutis[3]将木材横截面的二维数字图像看成是一种多维信号的集合,多图像进行分解,利用多方向的纹理信息对木材进行分类,正确率可接近91%。但是该类方法最大的问题在于无法做到无损检测,而且往往需要制作切片,识别效率低下。本文使用的是小倍率放大,该方法可以不用破坏木材原有的形态结构,同时也可以体现出木材的一定微观结构。
随着图像获取设备的迭代更新,高光谱图像成像仪成为了一种全新获取图像信息的手段。高光谱图像具有“图谱合一”的特性,在获取物体图像信息的同时也可以获取该物体的光谱信息。目前便携式小型高光谱成像仪走进实验室,该类光谱仪小型轻便可以和数字放大镜共同工作,方便采集木材微观结构的高光谱图像。
本文借助于美国SOC公司生产的SOC710VP高光谱成像仪对8种不同生长区域的木材进行了树种分类识别。首先使用波段选择方法选择了高光谱图像中最有代表性的若干个波段,然后利用分形思想提出了这些波段图像的多重分形曲线,最后融合了这些多重分形曲线找到了整个样本的特征向量。实验证明本文方法具有良好的分类效果。
2 材料与方法
2.1 材料
本实验的所有数据采集使用了美国SOC公司生产的SOC710VP高光谱成像仪,该成像仪的光谱范围为372.53~1 038.57 nm,共计128个波段,光谱分辨率为5.2 nm。拍摄到的显微高光谱分辨率为200×200×128。

表1 样本木材的详细资料Tab.1 Details of the sample wood

续 表
本文以8种木材横截面的高光谱图像为研究对象,具体木材样本资料见表1。每种木材采集120个样本,这些样本均来自不同的树木,为方便采集,首先需要对样本进行处理,处理方法如下:
首先需要将木材切割成若干个长与宽均为20 mm的条状样本,这些条状样本的侧面是木材的弦切面,顶面和底面是木材的横切面。然后使用圆盘锯将这个条状样本切割成若干高度为30 mm的小长方体,切割时注意其横切面平滑无毛刺,最后制作的样本长宽高分别为20 mm×20 mm×30 mm的小长方体。
每种木材样本的前96个小长方体作为训练集,从剩下的24个小长方体作为测试集。将这些样本在SOC710VP高光谱成像仪下完成高光谱图像采集,放大倍数为45×,图1为上述8种样本所采集的横截面图像。

图1 8种木材样本的横截面Fig.1 Cross-section of eight wood samples
2.2 高光谱图像的波段选择
高光谱图像可以看作是一个三维数据立方体。该三维立方体可以看成是由多张图片累积而成,每张图片的长与宽对应高光谱图像的长M与宽N,图片的数量多少对应高光谱图像的高L,图2中给出了高光谱图像的示意图。

图2 高光谱三维立方体示意图Fig.2 Hyperspectral three-dimensional cube diagram
高光谱图像往往具有几十至上百个波段,如果直接对这些波段进行处理,不仅处理速度慢也会影响分类精度的大小。所以在对高光谱图像进行处理时往往需要降维处理。目前高光谱图像的降维主要包含两类方法,一类是将高光谱图像做某种变换进行特征提取的方法,即寻找一个高光谱图像的低维投影,这类方法一般会改变高光谱图像的整体结构,降维后的高光谱图像与任意波段均不相同。代表方法有主成分分析(principal component analysis,PCA)、线性判别分析(linear discriminant analysis,LDA)、最小噪声分数(minimum noise fraction rotation,MNF Rotation)等。另一类方法是利用某种手段从现有的高光谱图像中挑选出若干波段的波段选择方法,这类算法挑选的结果是整幅高光谱图像的某一子集。代表方法有自适应波段选择(adaptive band selection ABS)、基于K-L的波段选择(Kullback-Leibler divergence,K-L)。本文主要侧重高光谱图像纹理分析与研究,故采用波段选择方法对高光谱图像进行降维。
2.2.1 自适应波段选择(Adaptive Band Selection)
自适应波段选择主要是通过波段信息量和波段与波段之间的相关性进行波段选择,具体描述如下[4]:
首先我们定义高光谱图像为A={b1,b2,b3…bi,…b128},其中bi代表高光谱图像的第i个波段。则第i个波段与第j个波段的相关系数定义为:

(1)


(2)
定义第i个波段的索引指数Ii为:

(3)
其中:上式中的Ri,j-1与Ri,j+1分别代表第i个波段与其前后两个波段的相关系数。值得注意的是这里的i,j∈[2,127]且i,j∈N*,最后选择的波段不包含第一个波段与最后一个波段。
Ii充分考虑了每幅图像的信息富集程度与相邻波段的相似性,Ii越大,相应波段的信息量就越大,也就是说该波段在整幅图像中越具有代表性。假设选择出的波段数量为n,则选择Ii较大的前n个波段即可完成波段选择[5-6]。
2.2.2 K-L散度(Kullback-Leibler divergence)
K-L散度是一种在信息论中得到广泛应用的信号相似度的度量方法,其定义为如下:设两个离散的概率分布函数分别为P=[P1,…,Pn,…PN]T和Q=[Q1,…,Qn,…QN]T,则Q相对于P的K-L散度为[5-6]:
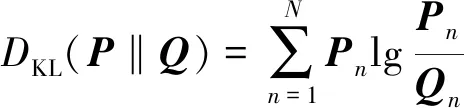
(4)
上式的物理意义是使用Q中的元素来表示P的所有元素所需要的额外信息量的大小,其单位与log的底数有关,当底数为自然常数时,其单位为nat;当底数为2时,其单位为bit。K-L散度越大,说明使用Q来表示P越困难[7]。


(5)
以此计算高光谱中任意两个波段的散度,得到矩阵对称矩阵D,设D中的第i行为ai=[D(i,1)…D(i,L)],ai中元素的平均值代表将第i个波段从数据集中删除后,所带来的损失。找到元素平均值最小的ai,去除该波段后重复上述算法流程再次去除波段,就可以得到含有信息量最大的n个波段[8]。
2.3 基于多重分形的高光谱图像纹理分类方法
分形和不规则的形状有关,是对图像自相似性的描述,由法国数学家Mandelbrot[9]于1975年提出。通过对自然景物纹理图像的研究进展,人们发现分形维数与图像粗糙度具有十分紧密的联系,作为一种非线性理论,分形理论可以很好的应用于研究不同木材的纹理特征。
其中计算分形维数的方法有很多,常用的有盒分法(box-counting)、随机游走法(Fractional Brownian motion)以及频域法[10-13]。针对不同的研究对象选择相应的分形维数作为度量,本文使用盒分法来计算分形维数其具体定义如下:
设F是Rn上任意非空的有界子集,Nδ(F)是直径最大为δ,可以覆盖F集的最少个数,则F的盒维数记为:

(6)
上述的盒分法可以计算一幅数字图像的分形维数。但是对于一幅数字图像来说,如果只使用一个分形维数对其进行描述,显然不能完全刻画其结构和特点。为此我们将一幅图像分成若干个小尺度,分别计算其分形维数,这样就可以获得多个分形维数,为更好的实现这一想法,我们引入图像密度函数。
图像密度函数表示了在测量点附近区域的一种不均匀性,其具体表达式如下:

(7)
其中:X(x,y)∈R2代表二维数字图像,B(X(x,y),r)代表一个中心为X(x,y)半径为r的正方形区域,f(B(X(x,y),r))代表对这个区域的一种运算,具体包含了以下3种方法[14]:
(1)基于图像亮度(强度)的函数运算:
f(B(X(x,y),r))=
∬B(X(x,y),r)(Gr*I)dX(x,y).
(8)
(2)基于图像梯度的函数运算,其中fk代表横向梯度与纵向梯度:
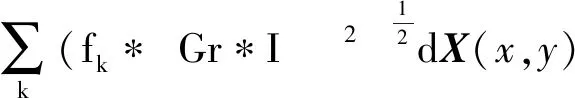
(9)
(3)基于拉普拉斯算子的函数运算:
f(B(X(x,y),r))=
∬B(X(x,y),r)|2(Gr*I)|dX(x,y).
(10)
以上3个式子中的“*”运算代表二维卷积运算,Gr代表高斯平滑核,其具体表达式如下所示,其作用是对图像起平滑作用。

(11)
图3是美国红橡的密度图像(r=4,δ=2)其中图3(a)利用图像梯度函数得到的密度图像,图3(b)是利用亮度函数得到的密度图像,图3(c)是利用拉普拉斯算子函数得到的密度图像。

图3 密度利用图像梯度函数(a)、亮度函数(b)和拉普拉斯算子函数得到的(c)图像函数。Fig.3 Density images by using image gradient function(a),luminance function(b),and Laplace operator functicn(c),respectively.
根据图3可知密度函数图像的像素取值范围主要集中在0~4之间。设步长为s=0.1,则整个密度函数图像的像素取值可被分为m个小区间如:(0,0.1],(0.1,0.2]….(0.1*(i-1),0.1*i]…(0.1*(m-1),0.1*m],整个图像可按照上述区间范围被分解成m个二值图像,其具体方法按式(12)计算:

(12)
我们使用计盒维数来估计图像的分形维数,计盒维数的算法如下:
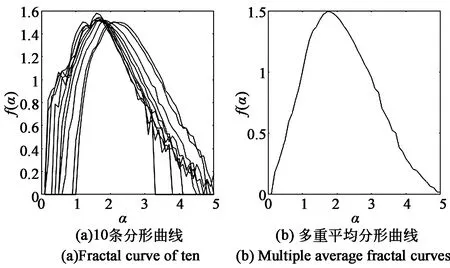
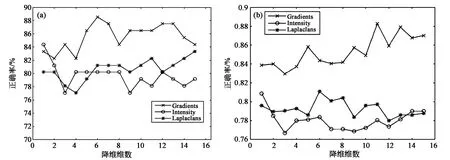
首先设一个长度为r(r∈{2,4,8,…,2n}∧2n 分别对这m个二值图像使用盒分法求解计盒维数,以小区间(0.1*(i-1),0.1*i]的右端点为横坐标α以该区间所对应二值图像的计盒维数f(α)=k作为纵坐标可以建立多重分形谱曲线。图4是根据图3采用不同密度图像所得到的多重分形谱曲线。 图4 3种不同密度图像所对应的多重分形谱曲线Fig.4 Multifractal spectral curves corresponding to three different density images 利用该方法可以对普通的数字图像进行分类,但通过实验发现,有多处重合并不能在木材微观结构的数字图像上得到理想的分类效果,这一点会在第三节中给出结论。 高光谱图像往往拥有百余个波段,并不能像正常上述的灰度图像那样求解其密度图像,为了能够提高效率并尽可能多地使用高光谱图像中的有用信息,必须使用降维方法对高光谱图像的多个波段进行选择,对所选波段求解多重分形谱。 假设通过2.3节的波段选择方法得到的波段为{x1,x2,…xn},使用上述方法求解每一个波段xi所对应的多重分形曲线yi(i∈[1,n]),这样就可以得到n个多重分形曲线,图5(a)中给出了美国红橡木材的一个样本在n=10时使用梯度密度函数图像所得到的10条多重分形曲线。 图5 高光谱图像10个波段的多重分形谱Fig.5 Multifractal spectra of 10 bands in hyperspectral images 在本节我们将与传统常用的纹理分类方法的准确率和运行时间作对比,本文与应用较多的传统方法灰度共生矩阵(GLCM)做对比实验,该方法的基本思想是使用PCA对高光谱图像进行降维,提取高光谱图像的第一主成分,使用第一主成分对应的图像利用灰度共生矩阵(GLCM)提取特征值,最后送入分类器进行分类。与多重分形做纹理对比试验,分类精度提升显著。 本文实验所使用的计算机配置为CPU:Intel I7-6700,内存:8 G,显卡:AMD Radeon R7 200 硬盘容量为1 TB。使用上述配置得到的各个算法的运行时间如表2所示。 表2 不同算法在各个阶段的运行时间Tab.2 Running time of different algorithms in each stage 从表2中可以看出主要影响运行时间的因素包含降维方法与函数密度计算,显然ABS降维方法的效率要远远高于K-L散度。函数密度中的亮度运行速度最快,拉普拉斯最慢。下面我们来看一下使用各种算法处理一个实验样本所需的时间。表3中给出了提取的波段数量为10时使用不同方法处理一个实验样本所需的时间。 表3 处理一个样本所需时间Tab.3 The time required to process a sample 从表3中可以看出,使用ABS作为降维方法和亮度密度函数求解分形曲线,速度最快,使用K-L散度作为降维方法和拉普拉斯密度函数求解分形曲线速度最慢。 我们使用PCA对高光谱图像进行降维,并将其第一主成分作为图像纹理分类对象。表4中给出了在SVM分类器下的混合分类正确率。 表4 使用PCA降维方法的分类正确率 方法训练集交叉正确率/%测试集正确率/%亮度密度函数69.0179.16梯度密度函数69.0180.20拉普拉斯密度函数73.3078.12GLCM67.6072.91 从表4中可以看出上述4种纹理分析法在PCA降维方法下的分类正确率略低,一方面原因在于使用PCA降维方法对高光谱图像进行降维时,高光谱的大量信息被压缩,这就导致正确率的下降。另一方面该方法对图像的尺寸大小具有严格要求,不同木材的横截面微观结构也具有一定的相似度。显然使用PCA提取高光谱的第一主成分这种方法在木材高光谱图像中并不十分适合。 图6是美国红橡树种使用亮度密度函数提取的波段选择数量n=15,8,2时的多重分形曲线。 图6 不同波段选择数量下的多重分形曲线。(a)n=15;(b)n=8;(c)n=2。Fig.6 Multifractal curves with different number of bands selected.(a)n=15;(b)n=8;(c)n=2. 通过图6可以看出,波段选择数量越大分形曲线越平滑,每条多重分形曲线的类内距离更近,这样在分类时就能得到更高的分类精度,这一结论可以在后面的分类正确率上得到证实。 为了能够更加准确地说明分类正确率,本文使用SVM与BP神经网络两种分类器对其进行分类。由于BP神经网络每一次的分类正确率并不稳定,所以本文的分类精度是在训练25次后所得到的平均分类精度。 图7、图8中给出了使用K-L散度和ABS作为波段选择方法的SVM分类精度与BP混合分类精度,可以看出使用梯度作为图像密度的K-L降维方法分类精度最高,在SVM下最高分类精度可达97.91%,在BP下最高分类精度可达90.83%。另外亮度和拉普拉斯方法均满足正确率先上升后下降的趋势,梯度方法随着波段选择数量增加而增加。造成这一因素的主要原因在于过多的波段选择数量会将一部分噪声融入平均分形曲线中从而造成正确率先升后降的现象。从整体上看在SVM分类器下梯度方法正确率高于其他两种方法,在BP分类器下亮度方法正确率高于其它两种方法。 图7 基于K-L降维方法的分类精度。(a)SVM;(b)BP。Fig.7 Classification accuracy based on k-l dimension reduction method.(a)SVM;(b)BP. 图8 基于ABS降维方法的分类精度。(a)SVM;(b)BP。Fig.8 Classification accuracy based on ABS dimension reduction method.(a)SVM;(b)BP. 表5中给出了不同方法下的最佳分类正确率所对应的波段选择数量。将表5和表4进行对比可发现,使用K-L波段选则方法和多重分形曲线对对木材的纹理进行提取可拥有更高的分类正确率。分类准确率最高可达到97.91%。 表5 不同方法下的最佳分类正确率与波段选择数量Tab.5 Optimal classification correctness and band selection number under different methods 本文重点研究高光谱图像中的纹理信息,对比分析了传统纹理识别方法GLCM和本文应用的多重分形提取纹理的方法做对比。结果表明,从运行速度角度分析,ABS降维方法优于K-L降维方法;从运行准确率角度分析,K-L降维方法高于ABS降维方法。其中在分类选择上我们都选择有监督分类,SVM分类效果高于BP,其中基于梯度密度函数的SVM准确率最高为97.91%。 本文采用纹理图像密度函数中的图像亮度函数、图像梯度函数、图像拉普拉斯算子函数运算不同盒维数值具有显著相关性。可以作为研究对象不同属性和指标进行研究。多重分形值可以作为基于纹理识别木材的重要参数,多重分形值与其它指标相结合进行木材识别与提取研究将成为下一步研究侧重点。

3 结果与讨论
3.1 不同算法的时间对比


3.2 使用PCA算法求解高光谱图像的纹理分类结果
Tab.4 Classification accuracy using PCA dimensionality reduction method
3.3 基于波段选择的多重分形谱纹理分类结果




4 结 论

