基于格的可验证秘密共享方案①

彭 咏,邵培南,李 翔,白建峰,孟珂举

1(中国电子科技集团公司第三十二研究所,上海 201808)

2(中国科学技术大学 计算机科学与技术学院,合肥 230026)

1 概述

秘密共享最早由Shamir[1]和Blakley[2]与1979年提出.秘密共享方案中存在一个可信的秘密持有者去分离一个秘密到多个不同的子份额.秘密持有者需要将子份额分发给多个子份额持有者.当秘密恢复时,子份额持有者互相交换子份额用于恢复秘密.为了避免子份额的持有者收到错误的子份额,可验证秘密共享允许子份额持有者去验证自己收到的子份额.后来的可验证秘密共享方案拓宽了原始的概念,使得可验证体现在以下两个方面:

1)秘密分发过程中,子份额持有者验证从秘密持有者获得子份额的完整性和正确性.

2)秘密恢复过程中,秘密恢复者验证从其他子份额持有者那获得的子份额的正确性和完整性.

秘密共享自提出之后就得到了广泛关注,并成为众多论文的研究热点[3–8].此外,可验证秘密共享是密码学方向中的一个重要领域.最早的方案是由文献[9]提出,用以抵抗非法参与者欺骗攻击来提高秘密共享方案的安全性.随后,文献[10]提出基于文献[1]的非交互式的可验证秘密共享方案.该方案利用离散对数的同态性去完成认证.其安全性是基于离散对数的计算难题假设.文献[11]总结并提出了一种公开秘密共享方案,在其中有一种特别的属性.任何一位参与者都允许检查自己收到子份额是不是正确的.

从方案设计角度来看,已经有很多种秘密共享方案被提出.大致可以分为两类.

第一类,通过通信来完成子份额的验证.大多数该类方案主要采用双变量多项式,该类方案主要问题在于,过多的通信导致验证低效.比如,当n个人参与恢复秘密时,我们需要两两验证子份额的合法性,总共需要进行轮通信.此外,在双变量多项式的秘密方案中,每个子份额是一个多项式.该类的秘密共享本身从信息率角度来看,即秘密和子份额信息熵的比值,是低效的.它的信息率是该子份额多项式维度的倒数.针对这其中的问题,后来的研究者主要研究如何能够降低通信复杂度.文献[12,13]已经展示了如果一个可被忽略的错误概率被允许的话,过去的通信复杂度边界不再适用.文献[14]在一个可忽略的错误概率被允许的情况下,给出了确切的通信轮复杂度.

第二类,采用数学难题来保证验证的安全性和有效性.很多该类可验证秘密共享方案,如著名的Feldman[10]和Pedersen[15]都是基于离散对数难题的.该类的方案主要特点,利用公开的参数信息进行验证,可以做到非交互式的验证.然而针对离散对数问题和大数分解难题,文献[16]中Shor给出了一个高效的量子算法.虽然Pedersen[15]更是在Feldman[10]的基础上,提出了无条件安全的可验证秘密共享方案,即安全性不依赖于数学难题.即使离散对数能被解决,也能保证子份额的安全性.但一旦出现这种情况,虽然能保证子份额的安全性,但方案将无法保持有效性,验证的过程可被任意伪造,方案不再有效.

因此,为了应对可能存在的量子计算机,保证方案的有效性,我们需要设计出一种可以抵抗量子攻击的新型无条件安全的可验证秘密共享方案.

本论文组织结构如下.在第2节,我们回顾一些基础的定义,概念和定理.在第3节,提出具体的可验证秘密共享方案并描述如何进行子份额的验证.在第4节,分析方案的效率安全性,比较其他的方案.在结束语中做出全文的总结.

2 基础知识

2.1 秘密共享

定义1.访问结构

使{p1,···,pn}代表所有参与者的集合.一个集合A⊆2{p1,···,pn}是单调的如果满足B∈A 并且B⊆C,则C⊆A .一个访问结构A ⊆2{p1,···,pn}是集合{p1,···,pn}的非空子集.A中的集合为授权集而任何不在A 均为非授权集合.则A 是该秘密共享方案的访问结构.

定义2.秘密共享[17]

假定K是秘密s的有限集合.一个分发方案∏ 和集合K实现访问结构 A 在满足下列条件下称之为秘密共享.

正确性:任意在A 中授权集合可以恢复秘密.

隐私性:任意不在A 中的非授权集不能得到关于秘密的任何信息.

2.2 格

格[18]是m维欧式空间Zm的n个线性无关向量组b1,b2,···,bn的整系数线性组合,即:

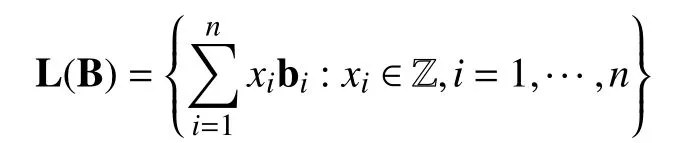
向量组 b1,b2,···,bn称为格的一组基.同一个格可以用不同的格基表示.m称为格的维数,n称为格的秩.有了格的定义,下面我们将简单介绍格上常见的数学难题,如:最短向量问题,γ-近似最短向量问题(SVPγ),最短线性无关向量问题.这些数学难题,已被用于构造基于格的公私钥密码方案.

最短向量问题(Shortest Vector Problem,SVP):给定格 L,找一个非零格向量v,满足对任意非零向量u∈L,∥ v∥≤∥u∥.

γ-近似最短向量问题(SVP-γ ):给定格L ,找一个非零格向量v,满足对任意格中的非零向量u ∈L,∥v∥≤γ∥u∥.

最短线性无关向量问题(Shortest Independent Vector Problem,SIVP):给定一个秩为n的 格L,找n个线性无关的格向量si,满足λi(L)=∥si∥,(i=1,···,n).其中λi(L)表示格L中第i个逐次最小的向量.

2.3 Ajtai单向函数[19]

选定适合的整数q,n,m满足条件m>nlogq,q=poly(n).令A ∈Znq×m为n×m的矩阵,矩阵中的元素均在 Zq上 .该矩阵包含m个 均匀随机的向量ai∈Znq,记为A=[a1|···|am],其中{a1,···,am}相互线性无关.

给定函数FA(x)=Ax(modq),x∈{0,1}m,反向计算出原像x的概率是可忽略的,其中,{ 0,1}m表示一个m位的0,1字符串.

上述单向函数的构造十分简单,且计算十分高效,他的安全性依赖于格难题.根据Ajtai文章[19]中结论,我们有如下引理.

引理1.如果格上的近似最短向量问题(SVP)和近似最短线性无关向量问题 (SIVP)是多项式时间不可解的,对于m>nlogq,q=poly(n),FA(x)是单向函数.

3 方案构造

本节介绍我们提出的可验证秘密共享方案.该方案示基于Shamir的(t,n)秘密共享,并且具有高效和抵抗量子攻击的特性.

3.1 符号

首先,定义Fp作为在素数p上的数域.Pi表示第i个参与者,si表示Pi用于恢复秘密的子份额并且si∈Fp.我们使用⊕ 代表异或运算.此外,用A ∈Znq×m表示一个由n个m维 线性无关向量组成的矩阵,其中n,m和q满足最后,记FA(x)等于Axmodq,其中x∈{0,1}m.

3.2 可验证秘密共享方案

该方案由以下3个步骤组成:初始化阶段,子份额分发阶段和秘密恢复阶段.

初始化阶段:

秘密持有者在Fp上 随机生成一个t−1 阶的多项式f(x):

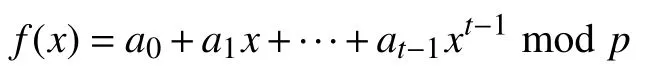
其中,秘密s即为多项式的常数项.也就是说,s=a0.此外,秘密持有者选择 整 数n,m和q满足m>nlogq,q=这里我们可以将Fp上的一个元素看成一个m比特的二进制字符串.最后生成m个线性无关的向量αi∈Znq,记为A :=[α1|···|αm].

分发阶段:

(1)秘密持有者计算si=f(xi)并且随机从{ 0,1}m中选择ti,将(si,ti)一 起发送给子份额持有者Pi.注意到如果sisj且titj,那么si⊕ti一定不等于si⊕tj.

(2)秘密持有者公开矩阵A,FA(si⊕ti)和s′i的值,其中s′i=si⊕ti.

(3)子份额持有者Pi收到(si,ti)后,首先要对自己接收到的子份额进行验证:

如果验证所得到的子份额是正确的,那么继续以下的骤,如果验证失败,则要求秘密持有者重新发送子份额.

秘密恢复阶段:

假设有k个子份额持有者参与恢复秘密s,其中k≥t,他们需要执行以下步骤:

(1)子份额持有者之间互相验证对方子份额的合法性,具体操作如下:

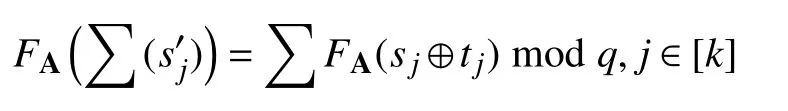
如果验证正确,则继续下边的步骤.否则,我们可以通过以下操作检查每个参与者的身份从而确定哪个是非法的参与者.

(2)参与秘密恢复的子份额持有者互相交换信息si并用所得到这些子份额采用Shamir秘密共享的方式去恢复秘密.

为证明验证秘密恢复阶段步骤(1)的正确性,我们给出定理1.

定理1.单向函数FA具有线性同态的特性,并且满足以下公式:

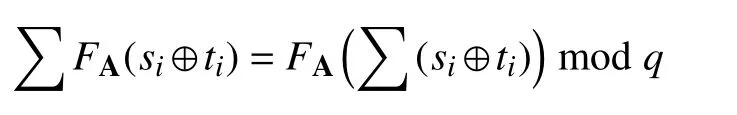
证明:假设有k个子份额持有者组成的授权集合,他们的子份额构成Γ ={s1,···,sk}.每个Γ 中的si均绑定一个对应的随机值ti,所有的si和ti都 是从{ 0,1}m中选取的.使用 A∈Znq×m表示一个由n个m维线性无关向量组成的矩阵,也就是说A :=[α1|···|αm].那么有:

此外,因为 (si⊕ti)仍然是一个m比特位的二进制字符串,可以被写为因此,上述公式等于:

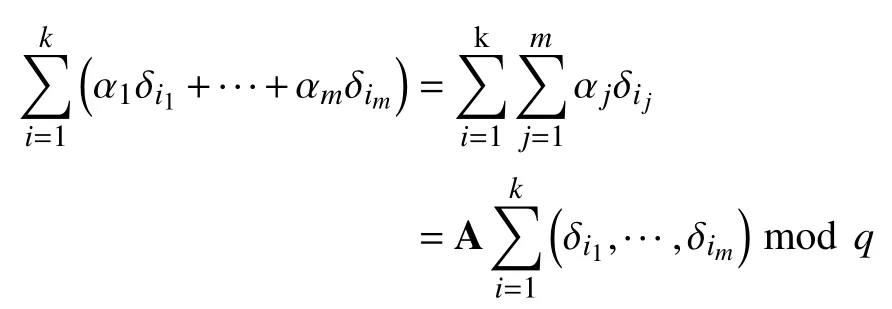
因此,函数FA有线性同态性并且该定理成立.

4 分析

在本节,我们分析提出方案的效率以及安全性.事实上,我们的方案就是将Ajtai单向函数函数应用到Shamir方案中,同时引入随机变量ti,使得可验证方案是无条件安全的.即使最终格难题被破解,也无法获得关于子份额的任何信息.当然方案的有效性仍然依赖于格难题.

4.1 效率分析

首先,我们需要考虑方案的信息率.信息率是作为衡量一个秘密共享系统的重要手段,被广泛用于衡量秘密共享方案本身的效率.信息率 σ 被定义为秘密长度与最大子份额长度的比值,也就是说:

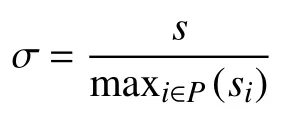
在我们的方案中,因为子份额不仅仅是单独的si,而是一对值(si,ti).因此,该方案的信息率为1/2而不是1.此外,还有以下一些指标用于衡量可验证秘密共享方案的效率:

(1)验证子份额时所要通信的轮数.

(2)子份额持有者用于验证子份额合法性所需的通信数据量.

(3)子份额持有者验证子份额合法性所要做出的运算量.

指标(1)和(2)用于衡量通信的效率,也是大多数分析通信协议通信复杂度的指标.指标(3)用于衡量计算的效率.

可验证秘密共享的轮数复杂度主要是在实际方案设计中需要考虑的.通信轮数相较于通信量来言,往往需要更多的时间.因此,在实际的通信协议中往往作为重要因素被考量.我们的方案类似于方案[9,16],是非交互式的可验证秘密共享,在分发阶段,并不需要在验证时额外交互信息.在秘密恢复时,仅仅只需要将自己的验证信息广播出去即可,所以不会提高通信轮数,通信的轮数复杂度可被忽略.

子份额持有者用于验证子份额合法性所需的比特数可以被分为以下两部分:秘密持有者分发的信息和子份额持有者之间互相交互的信息.第一部分与其它可验证秘密共享方案差别较大而后一部分和其它可秘密共享方案大致相同,因此我们主要分析第一部分的信息量.在我们的方案中,秘密持有者需要公开一个矩阵A ∈Znq×m和FA(si⊕ti)的值.它总共包含的比特数如下:

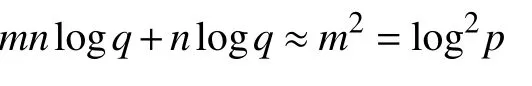
在本文中,计算开销是可以预估的.为了更好的说明,我们比较我们的方案与其它3篇基于Shamir秘密共享的可验证秘密共享方案.假设所有的秘密和子份额的空间都是在Fp,我们将Fp上一次乘法运算记为1次运算.

我们只在此比较子份额持有者用于验证其它子份额合法性所需要的计算量.在我们的方案中,子份额持有者仅仅需要在很小的整数中进行线性运算.总共所需要在Zq中 执行nlogp乘 法运算,其中l ogp>nlogq.为了方便比较计算复杂度,我们通过除以 2n将我们的结果从Zq转化到Zq.

下面我们将从通讯量,计算量和适用性3个方面,比较本文方案和以往方案.通讯量是秘密恢复阶段,每个参与者需要广播多少比特的验证信息.计算量是每个在于者在最坏情况的计算复杂度来表示.比较结果如表1所示.

在表1中,Schoenmakers的方案[20]取决于公钥密码,所以无法进行评估.此外,我们使用“普适”去代表我们方案的适用性.它代表我们的方案可以应用于任何的方式构造的秘密共享方案中,例如基于拉格朗日插值多项式,基于中国剩余定理,基于超平面空间,基于线性码等密码共享方案.显然,我们的方案相对于其它可验证秘密共享方案具有更好的计算效率.

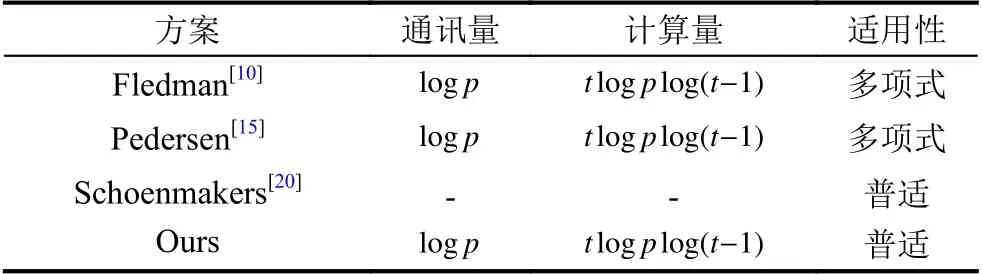
表1 本方案与已有方案的性能比较

4.2 安全性分析

我们的方案是基于Shamir秘密共享,所以任何授权集合都应该能够恢复秘密而任何的非授权集合都不应该能恢复秘密.此外,我们还需要考虑验证过程的安全性,也就是说子份额持有者在验证子份额合法性时是否泄漏了秘密.

定理2.本文方案的验证机制,包括分发和秘密恢复过程,基于Ajtai单向函数,满足不可区分和不可伪造特性.

证明:在我们的方案中,si⊕ti满足均匀随机分布.此外,Ajtai单向函数FA(si⊕ti)是均匀随机分布.我们不能够区分所以该验证机制满足不可区分的特性.

为了证明绑定特性,我们需要证明不存在 概率多项式时间的算法去找到两个不同的si.也就是说,不存在 概率多项式时间的算法去找到sisj∈{0,(1}m使)得Asi≡Asj(modq).如果我们找得到,那么存在0(modq).因为sisj∈{0,1}m,我们有构成了一个针对格难题中小整数问题的一个解法,而小整数问题被认为是一个不可解的数学难题.因此,本方案中验证机制满足不可伪造性.

我们已经证明了我们方案的验证机制满足不可区分和不可伪造两个特性.不可区分特性意味着方案的验证过程不会泄露秘密的任何信息.不可伪造特性意味着只有正确的子份额才能通过验证.在上述证明过程中,不可区分和不可伪造均是依赖于格难题.

定理3.即使Ajtai单项函数被破解,验证子份额的过程也不会泄露任何秘密的信息.

证明:根据引理1,我们知道Ajtai单项函数可以被约简为格难题中的近似最短线性无关向量问题.至今还没有任何多项式时间的算法去解决近似最短线性无关向量问题.假设近似最短独立向量问题和Ajtai单项函数都被破解,攻击者可以从FA(si⊕ti)得 到值si⊕ti.因为ti是 在子份额空间中的随机值,所以si⊕ti是随机分布在子份额空间的,从而我们无法从si⊕ti得到任何秘密的信息.这就表明了,即使Ajtai单项函数被破解,验证子份额的过程也不会泄露任何秘密的信息.

通过以上证明,我们得到我们的方案是无条件安全的.换言之,格难题保证了可验证的有效性,即使格难题被破解,我们的方案依旧不会泄露子份额的任何信息.即本方案的验证机制是无条件安全的.

5 结束语

我们在本文展示了基于格的可验证秘密共享方案,能够在秘密分发和恢复过程中,验证子份额的合法性.同时该方案具备无条件安全的特性,即使格难题被其他什么未知工具破解,也能保证子份额的安全性.

本方案通过与已有方案的比较,我们的方案具有以下特性:更高的效率;量子攻击抵抗性;普适性(可以应用于任何数学工具实现的秘密共享方案).