异重流水卷吸经验式不确定性对层平均数学模型的影响

（浙江大学 港口海岸与近海工程研究所，浙江舟山316000）

泥沙异重流常发生在水库和高含沙河流等区域，如长江深水航道区浮泥沿河床运动形成的异重流现象[1].异重流在人类的生产生活中有着广泛的应用，合理利用异重流排沙可以减小水库淤积和航道淤塞.国内外学者通过野外观测、实验和数值模拟对异重流取得了丰硕的研究成果[2－5].特别是异重流数值模拟，随着计算机科学的进步，取得了飞速的发展.层平均模型在异重流的数值模拟研究中得到了广泛的应用[6－11].层平均模型不可避免地要引用泥沙侵蚀、水卷吸和泥沙沉速等经验关系式.其中，水卷吸经验关系式的精确度对数学模型的计算结果影响很大.这是因为，异重流的驱动力来自其与环境流体之间的密度差，而水卷吸经验式的计算结果代表环境水体进入异重流的水量，若卷吸水较多，则使得含沙量较低，反之则含沙量高，并因此影响密度差和驱动力.

早在1959年，Ellison等[12]建立了异重流卷吸水量与理查德森数的经验式.在此基础上，范家骅[2]认为急流时泥沙异重流的水卷吸同盐水异重流类似.Parker等[13]结合少量的持续入流式异重流水卷吸实验数据，对Ellison经验式进一步修正，修正公式在异重流层平均模拟中得到了广泛应用.然而，异重流发生在水下，不易观测到，且其与背景流体的交界面环境非常复杂（湍流、开尔文－赫姆霍茨（K－H）不稳定性），要量化这个区域是个挑战，需要获取大量高精度野外及实验数据来进一步率定水卷吸经验式.当实测数据增加或存在误差时，采用传统最小二乘法拟合得到的经验系数值极可能发生变化，这使得异重流水卷吸经验式具有较大的不确定性.比如，Ottolenghi等[14]指出，Parker的水卷吸经验式[15]可能会低估开闸式异重流水卷吸量一个量级.

Traer等[11]采用基于贝叶斯定理的 Monte Carlo方法（以下简称概率法），首次尝试了对异重流水卷吸经验式进行不确定性分析，并探讨了其不确定性对异重流经典四方程模型的影响.Traer所采用的概率法相较于以最小二乘法为代表的传统拟合方法有很大优势，因为通过经验系数样本与实测数据拟合优劣的比较筛选过程，可以得到经验系数的大量样本，用以分析其均值和标准差等统计特性，而传统拟合方法得到的是固定的经验系数取值.然而，Traer所采用的异重流四方程模型具有恒定流和忽略地形冲淤过程的假设.一方面，恒定流的假设显然不能全面地描述异重流随时间的变化；另一方面，异重流运动过程中造成的地形冲淤，以及地形冲淤对异重流演化的反作用不能轻易忽略[9－10].Traer等采用四方程模型的可能原因是：异重流三方程模型（包括水沙混合体质量守恒、动量守恒和泥沙质量守恒）模拟自加速异重流时高估了泥沙侵蚀量，消耗过多能量，产能小于耗能从而不满足能量平衡，与异重流自加速本质相反.然而，Hu等[16]通过理论推导和数值实验发现，三方程模型并没有破坏能量平衡.实际上，泥沙侵蚀量越多，异重流传播时有越多势能转化为动能，增加产能，满足能量平衡.

因此，本文考虑异重流非恒定特性、地形冲淤和地形冲淤对异重流演化的影响，研究异重流水卷吸经验式对三方程模型框架下异重流层平均水沙耦合数学模型计算结果的影响.具体而言，本文结合现有异重流水卷吸实验数据，应用基于贝叶斯定理的Gibbs随机采样方法，采样获取了异重流水卷吸经验式中经验系数组合的大量样本；然后，将经验系数样本值代入异重流层平均水沙耦合异重流数学模型（以下简称耦合模型），模拟陡坡上异重流演化过程，从而讨论经验系数不确定性对模型计算结果的影响.

1 水卷吸经验式不确定性研究方法

1.1 水卷吸经验式的简介

Parker等[13]基于异重流实验数据，得到了水卷吸经验式：

式中：ew为水卷吸系数；E1＝2.4，E2＝0.5，为Parker率定的经验系数取值；Ri＝Rgφh／u2为理查德森数，R为有效重力，g为重力加速度，φ为层平均泥沙的体积分数，h为层平均厚度，u为层平均速度.

1.2 基于贝叶斯定理的Gibbs采样法

用Data指代实测值（即Parker等[13]在可侵蚀底床上所做持续入流式异重流实验中获得的相关Ri和ew的数据，共53组），用m指代经验系数组合，m＝ （E1，E2），用P（m｜Data）表征给定实测数据时，经验系数某组取值的概率.根据贝叶斯定理[17]有

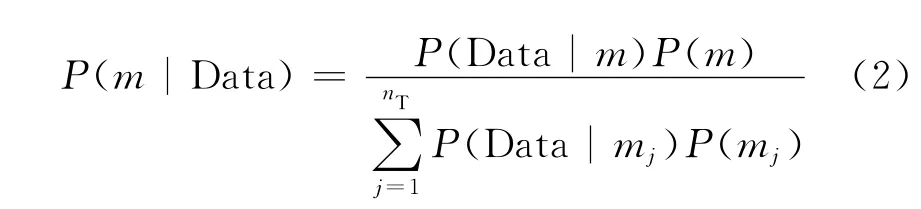
式中：下标j表示经验系数样本的序号；nT＝2×105为总样本数；P（m）为先验分布（即无实测数据条件下，经验系数取值的概率）；P（Data｜m）为似然函数，即对于给定的经验系数取值，式（1）计算值与实测值之间的拟合程度.由于每个经验系数的取值受到实验条件和测量数据准确性等很多因素的影响，符合中心极限定理，所以本文假设经验系数取值符合正态分布，采用 Gibbs采样法[18－19]，分别对E1和E2进行循环采样.采样过程叙述如下.

任意选取一组经验系数值 （E1，0，E2，0）作为初始值；先固定E2，0不变，以E1，0为均值，以E1，0σE1为标准差（σE1为E1，0先验概率的标准差），随机取得一个新的备选系数样本值，将其记为E＊1，则E＊1的接受概率[20]为

式中：f（E1，0｜E＊1）为以E＊1为均值，E＊1σE1为标准差的正态分布在E1，0处的值.当ra大于一个[0，1]之间的随机数时，接受E＊1并以（E＊1，E2，0）为新的起点.固定E＊1，使用同样的方法对E2，0进行采样.如此循环，在采样的过程中，不断采取以下方法对样本频次进行统计：以每个样本点为圆心，0.2为半径作圆，统计圆内点的频次.结果表明，当采样所得的（E1，E2）样本数达到2×105后，继续增加样本数量对样本集合的频次分布不再产生影响，本文认为采样已经收敛，停止采样.

Gibbs法的关联性采样体现在两个方面：① 由于每个样本的入选仅与上一个样本相关联，所以在采样过程中，如果待选（E1，E2）样本能够比上一个样本更好地拟合实测水卷吸数据（似然函数值较高），则该样本能够以更高的概率被接受；② 每组（E1，E2）样本之间相关联，如果一组（E1，E2）样本使得水卷吸计算值和实验值差距较大（似然函数小），则该组样本的接受概率就小.基于上述认识可以预期的是，在通过足够数量的采样后，能够使得水卷吸实验值和计算值拟合越好的（E1，E2）样本频次越高.

2 经验系数的样本分布

得到样本点在（E1，E2）平面的分布后，进一步得到25%nT、50%nT、75%nT和95%nT的（E1，E2）样本所在的区间范围，如图1所示，其中黑色十字为概率最大样本（E1，E2）＝（2.38，0.52）.颜色由深至浅，依次为25%nT、50%nT、75%nT、95%nT样本的区间范围.占总样本95%的E1、E2取值组合中，E1和E2的区间范围分别是[0.96Em1，2.72Em1]和[3×10－4Em2，6.59Em2]，Em1和Em2分别为概率最大的E1和E2值（即以该点为圆心，0.2为半径的圆内，样本频次最高的值）.

图1 E1和E2不同比例样本所在的区间范围Fig.1 Interval of different proportions of E1and E2

图2显示了概率最大系数组合与最小二乘法拟合结果（E1，E2）＝（2.38，0.52）的对比情况，图2（a）为代入概率最大系数组合的式（1）与实测数据的拟合图像，图2（b）为原经验式与实测数据的拟合图像.可以看出，概率最大系数组合与原公式拟合结果相近.

图2 概率法拟合的经验式与原经验式对比Fig.2 Comparison between the empirical formula fitted by probability method and the original formula

3 系数不确定性对数学模拟的影响

3.1 层平均水沙耦合异重流数学模型

在层平均假设下，非恒定的水沙耦合异重流数学模型可写成如下守恒形式[9－10]：

式中：U为守恒变量向量；F为通量向量；Sb为几何源项向量；Sf为底床摩擦、底床变形、水体卷吸等源项向量；z为底床高程；E＝ωEs和D＝ωφb分别为泥沙上扬通量和沉降通量，ω为泥沙沉速，Es＝8.9×10－9Z5m／（1＋8.9×10－9Z5m／0.3）为泥沙侵蚀系数[21]为泥沙雷诺数，R＝ （ρs－ρw）／ρ为有效重力，g为重力加速度，Ds为泥沙粒径，ν为水的运动黏滞系数，φb＝r0φ为近底泥沙的体积分数，r0为近底与水深平均泥沙体积分数的比值；x为水平坐标；t为时间；g′＝Rgφ为水下有效重力加速度为摩阻流速，cD为拖曳系数，rw为异重流上下界面阻力比值；ρ＝ρw（1－φ）＋ρsφ为水沙混合体密度，ρ0＝ρwp＋ρs（1－p），ρw为清水密度，ρs为泥沙密度；p为床沙孔隙率.控制方程使用有限体积法进行离散[9－10]，并采用正方形网格，则有

式中：Δx为空间步长；Δt为时间步长；上标n和 ＊代表时间节点号；i代表空间节点号；Fi＋1／2和Fi－1／2为体积单元间的通量向量；Sb，i为底坡源项在第i个空间单元的计算值.时间步长需满足CFL收敛条件.

本文将Parker推导的陡坡上异重流自加速临界“点火条件”作为边界条件，在这些初值条件下的异重流，从底床和环境水体获得的能量高于其耗散，在沿程运动时会不断加速，故称为“自加速”异重流，这种异重流在实际生活中应用广泛[8－9，11]：x＝0处，h＝2.0m，u＝0.801m／s，φ＝0.006 09.其他参数：g＝9.8m／s2，ω＝ 0.75cm／s，r0＝ 1.6[13]，cD＝0.004，Ds＝0.01cm，ν＝1×10－6m2／s，ρw＝1 000 kg／m3，ρs＝2 650kg／m3，p＝ 0.4，rw＝0.43.计算区域为6 000m，空间步长1m，时间步长1s，出口为自由出流.

3.2 （E1，E2）组合对异重流模型的影响分析

由于不同的（E1，E2）样本值代表了不同的环境流体进入异重流的清水量，进而影响异重流与环境流体的密度差及其运动速度，为了使所有单个异重流算例均能流过最后一个统计断面（1 000m），且尽可能提高计算效率，现随机选择5 000组样本输入模型并记录其运动时间和运动距离.通过测试，当计算时间为2 200s，计算区域为6 000m时，所有算例均符合要求.

由于篇幅所限，现选择概率最大经验系数值所对应的异重流在4个典型时刻（100，200，300，400 s）的厚度h、速度u、泥沙体积分数φ、底床形变Δzb（初始时刻时为0），如图3所示.其中，x表示与进口边界的距离.

图3 不同时刻异重流水力参数Fig.3 Turbidity current hydraulic parameters at different times

从图3中可以看出：随着异重流运动时间的增加，厚度和速度增加明显，且增速在加快；泥沙体积分数先增加后减小；而底床被侵蚀得越来越多.

将所有（E1，E2）样本值输入上述异重流耦合模型，计算异重流过程，以x＝100m断面为例，将计算所得水力参数范围（0.53m≤h≤6.19m，0.98 m／s≤u≤2.30m／s，0.01≤φ≤0.11，－6.18m≤Δzb≤－2.91m）分为50等份，对每个区间作频次（n）统计，结果如图4所示.若计算水力参数的范围越大，（E1，E2）不确定性对异重流计算结果的影响就越大.从图4可以看出，厚度最小值频次较高，速度和泥沙体积分数的较大值频次高.比如，厚度区间0.53～0.64m的频次为69 981，占比约37%，随着厚度的增大，频次逐渐降低，计算速度和泥沙体积分数有类似但相反的规律.底床形变的最小值和中间值（－4m左右）频次都较高.－6.19～－6.12m区间的频次为14 159，占比7%；－4.22～4.15m区间的频次为33 947，占比18%；其他区间占比普遍低于3%.

为解释这一现象，并了解样本空间内不同样本输入模型计算所得的异重流水力参数分布情况，将E1样本范围[－3，7]以及E2样本范围[0，4]等分为100份，得到10 201组（E1，E2）.首先输入耦合模型，得到10 201组计算结果，并取x＝100m断面处计算结果作等值线，结果如图5所示；然后输入式（1）得到的10 201组ew计算值，作等值线，结果如图6所示.

以图5（a）为例，根据0.9m厚度等值线，将E1－E2平面分为两个区域，区域I中ew较小，区域II中ew较大（图6）.当（E1，E2）取区域I样本值时（该区间样本频次为97 357，占比达51%），ew较小，计算的厚度相应较小；当（E1，E2）取区域II样本值时（频次93 214，占比达48%），ew较大，计算所得厚度较大，但是由于区域I的厚度范围（0.53～0.9m）较区域II的厚度范围（0.9～6.19m）小，所以频率分布图4（a）中出现了最小值频次最高的现象.以异重流速度等值线图5（b）为例，根据2.118m／s速度等值线，可将平面分为3个区域.当（E1，E2）取区域I样本值时（频次22 658，占比12%），速度区间范围为2.113～2.118m／s；当（E1，E2）取区域II样本值时（频次80 235，占比42%），速度区间范围为2.118～2.3m／s；当（E1，E2）取区域 III 样本值时（频次87 079，占比45%），速度区间范围为0.98～2.113 m／s，虽然区间III的样本频次较高，但是其速度的范围较大，所以图4（b）中出现了较大速度频次高的现象，泥沙体积分数和底床形变的频率分布图可以使用同样的方法分析予以分析，不再赘述.

图4 异重流水力参数的频次统计（x＝100m）Fig.4 Frequency statistics of the hydraulic parameters（x＝100m）

图5 E1－E2平面上计算异重流水力参数的等值线图（x＝100m）Fig.5 Equivalent line of the hydraulic parameters on the E1－E2plane（x＝100m）

图6 E1－E2 平面ew 的等值线与（E1，E2）样本分布图（Ri＝0.3）Fig.6 Equivalent line of ewon E1－E2plane and （E1，E2）sample distribution（Ri＝0.3）

将概率最大（E1，E2）取值输入数学模型，计算所得各断面水力参数分别记为hr、ur、φr和 Δzbr（以下简称标准值）.将（E1，E2）样本值输入数学模型计算所得水力参数（h、u、φ、Δzb）分别除以各断面水力参数（hr、ur、φr、Δzbr），比较该倍数的变化情况，可以定量分析经验系数不确定性对数学模型计算结果的影响.图7给出了4个典型断面（100，200，500，1 000m）上h／hr、u／ur、φ／φr、Δzb／Δzbr的范围，并通过颜色的深浅区分了25%、50%、75%、95%样本对应的该比值的范围.图中黑色虚线代表标准值随空间的变化.

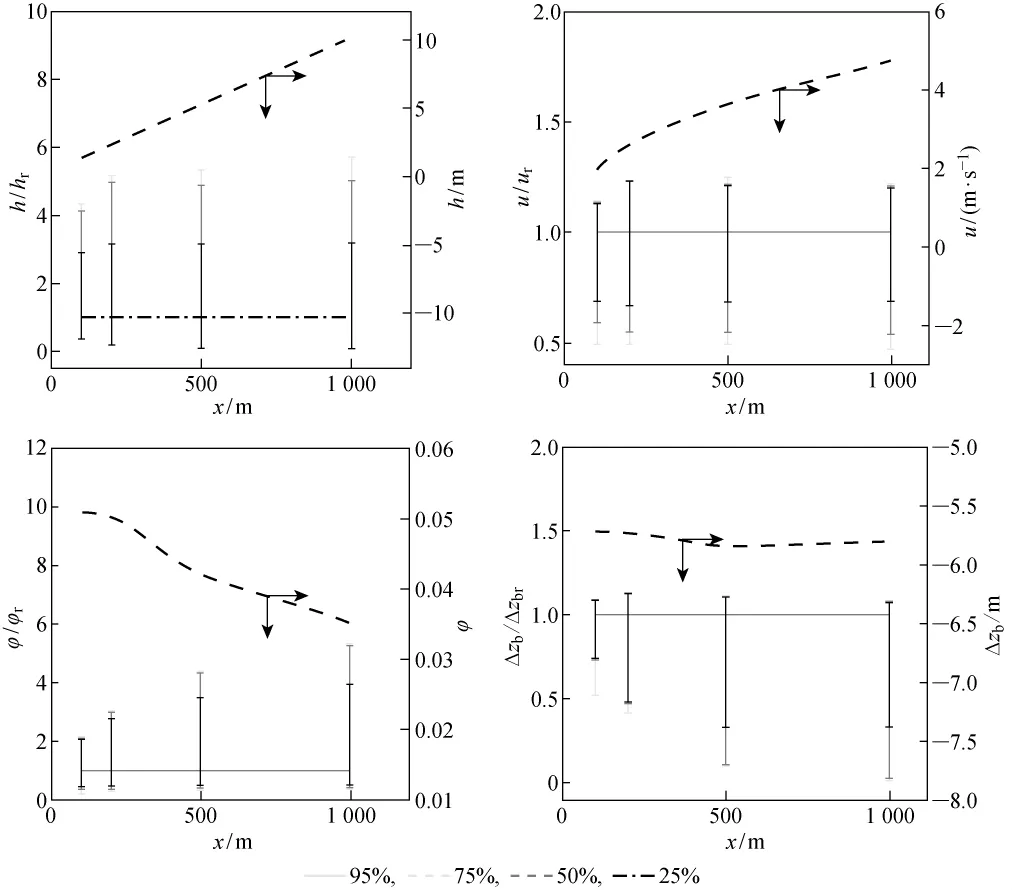
图7 不同比例（E1，E2）样本计算的异重流水力参数在4个断面的区间范围Fig.7 Interval of turbidity current hydraulic parameters calculated by different proportions of（E1，E2）

由图7可知，随着距进口距离的增大，计算厚度和速度的标准值迅速增大、泥沙体积分数标准值迅速减小、底床形变标准值变化不大.95%（E1，E2）样本计算得到的比值（h／hr、u／ur、φ／φr、Δzb／Δzbr）范围也随着距离增大而增大.这说明，（E1，E2）不确定性对计算水力参数的影响随着与进口边界距离增大而增大.在x＝500m处，95%样本计算的厚度是标准值的0.06～5.35倍、计算速度是标准值的0.49～1.24倍、计算泥沙体积分数是标准值的0.37～4.35倍，计算底床形变是标准值的0.1～1.11倍；到x＝1 000m处，计算水力参数与标准值之间倍数扩大至0.03～5.73（厚度）、0.46～1.23（速度）、0.39～5.31（泥沙体积分数）和0.01～1.08（底床形变）.由图7可见，随着距离的增加，95%样本计算所得水力参数的范围远大于25%样本计算所得水力参数范围，这说明异重流数学模型对水卷吸经验式中经验系数（E1，E2）的取值十分敏感.比如，在x＝500m处，95%样本计算的厚度是标准值的0.1～3.16倍，比25%样本的范围扩大了72%，计算速度、泥沙体积分数和床面形变也有类似现象.通过上述分析可以看出：经验系数（E1，E2）对数学模型的计算结果影响很大，且随着距离的增加，经验系数不确定性对模型的影响在逐渐增大；概率最大（E1，E2）值代入数学模型可能低估异重流厚度和泥沙体积分数，高估异重流速度和床面形变.

4 结论

（1）本文应用基于贝叶斯定理的Gibbs随机采样法得到 概率最大 系数组 合 （E1，E2）＝ （2.38，0.52），与原公式的取值（E1，E2）＝（2.4，0.5）相近，该方法可以作为最小二乘法等传统经验式拟合方法的重要补充.

（2）比较（E1，E2）不同比例样本计算结果在不同断面的区间范围，可以看出：相同比例样本输入模型计算得到异重流水力参数区间范围随运动距离的增加逐渐增大；经验系数不确定性对数学模型的计算结果影响逐渐增大；采用概率最大经验系数值可能低估异重流厚度和泥沙体积分数，高估速度和底床形变.

（3）比较不同比例（E1，E2）样本输入数学模型得到的同一断面计算水力参数区间范围可以发现，在x＝1 000m 处，95% （E1，E2）样本计算得到的厚度范围比25%样本计算所得厚度范围扩大了83%，说明模型对（E1，E2）系数组合的取值十分敏感.

由于概率最大经验系数取值输入模型预测的异重流水力参数可能出现偏差，所以下一步将在两个方面开展工作：① 增加实验数据获取，以便对经验系数的取值进行更加准确的率定；② 开展不同水卷吸经验式不确定性对数学模型影响的比较，为经验式选择提供依据.