近爆作用下钢筋混凝土柱数值分析加载方法对比

闫秋实，陈天一，廖维张

(1.北京工业大学城市与工程安全减灾教育部重点实验室，北京 100124；2.北京建筑大学工程结构与新材料北京市高等学校工程研究中心，北京 100044)

近些年来，世界恐怖爆炸袭击事件频发. 另一方面，我国加工厂越来越多,化工品泄露爆炸、粉尘爆炸和燃油泄露爆炸、家用燃气泄漏爆炸等意外爆炸事件时有发生. 钢筋混凝土柱作为建筑主要承重和传力构件，其抗爆性能好坏直接关系到结构的抗爆乃至抗连续倒塌性能.

国内外学者对爆炸荷载作用下钢筋混凝土柱损伤破坏做了大量数值计算研究. Shi等[1]、高飞等[2]对爆炸荷载作用下钢筋混凝土柱的动力响应细致研究，采用等效三角形荷载以均布形式施加在柱表面，这种加载方法适合炸药距离柱较远的情况，但在近爆作用下，荷载沿柱呈现明显的不均匀分布，需要对荷载简化研究[3]. Kyei[4]、Wu等[5]、龚顺风等[6-7]、闫秋实等[8]采用“炸药- 空气- 柱子”流固耦合(以下简称流固耦合)的方法对柱子的抗爆性能进行参数分析. 徐慎春等[9]采用Load blast命令(以下简称Load blast)对钢管混凝土柱进行数值模拟和试验验证，但钢筋混凝土柱数值模拟中采用这种加载方式的情况较少.

从相关文献可以看出，国内外学者对爆炸荷载作用下钢筋混凝土柱动力反应及损伤破坏数值模拟研究，其爆炸荷载加载方式各有不同，近爆作用下钢筋混凝土构件数值模拟加载方式的对比研究仍为一个空白. 高飞等[10]提出爆炸荷载的施加不同，造成计算结果差异. 本文对近爆作用下钢筋混凝土柱进行数值模拟，提出爆炸荷载简化模型(以下简称荷载简化)并与Load blast和流固耦合加载方式进行对比，为近爆作用下钢筋混凝土构件的数值分析提供必要的参考.

1 试验介绍

北京建筑大学廖维张课题组进行1组钢筋混凝土柱抗爆试验. 钢筋混凝土柱截面尺寸为300 mm×300 mm，柱高3 000 mm，保护层厚度30 mm，混凝土等级C40，纵筋等级HRB400级，箍筋等级HRB335级，纵向受力钢筋采用对称布置，配置4根20 mm的HRB400级钢筋，配筋率为1.4%，箍筋采用直径10 mm，考虑抗震等级为二级，间距分别为100、200 mm，沿柱高均匀布置. 普通柱配筋详图见图1，制作完成的构件见图2. 试验选取炸药装量为7.6 kg，爆炸距离(TNT炸药中心至结构表面)为0.6 m，比例距离为0.3 m/kg1/3，试验装置见图3，图4为试验装置示意图.

2 近爆作用下钢筋混凝土柱表面荷载简化计算

2.1 AUTODYN数值模型建立

在AUTODYN数值分析中所采用的材料参数及属性均取自AUTODYN自带的标准材料模型库[11]. 空气状态方程采用理想气体状态方程

p=(γ-1)ρ0e0

(1)

式中：空气绝热指数γ=1.4；空气密度ρ0=1.225 mg/cm3；空气初始能量密度e0=206.8 MJ/kg. 炸药采用TNT，状态方程为JWL状态方程

(2)

式中：ω=0.35；r1=4.15；r2=0.9；C1=374 GPa；C2=3.74 GPa；ν为比容. 炸药的爆速为6.93 km/s，TNT炸药初始密度ρ=1.63 g/cm3，爆压为21 GPa.

由文献[3]可知柱的刚度对柱表面爆炸荷载影响较小，柱子采用水泥混凝土材料，其密度为2.75 g/cm3，初始紧缩压力P为23.3 MPa，剪切模量G为16.7 GPa，体积模量E为35.27 GPa，抗压强度σC为35 MPa.

采用2D、3D的映射方法建立1/4模型以提高计算效率减少计算时间，首先建立2D炸药模型，见图5(a)，计算到爆炸波传递到柱表面之前停止. 然后，将计算好的2D炸药模型映射到3D模型中，见图5(b).

在数值模拟中，柱采用Lagrange单元模拟，炸药和空气采用Euler单元模拟. 流固耦合采用AUTODYN提供的Euler/Lagrange全接触算法[11]. 图6给出有限元模型的三视图，其中柱子的两端固结并标出有限元模型的边界条件.

2.2 超压峰值沿柱分布及简化

选取等间距测点提取超压ΔP1曲线，见图7，图中h为距柱底高度. 冲击波遇到混凝土柱形成反射超压，其峰值沿着柱高度方向向两端逐渐衰减，离柱高度中心越远，前后2个压力峰值之间的时间间隔越长，意味着冲击波传递速度慢，体现出钢筋混凝土柱对空气冲击波的黏滞作用，但钢筋混凝柱对冲击波在其上作用时间影响不大. 超压峰值沿柱高分布见图8，沿柱宽方向柱中线的超压峰值明显高于柱两边缘的超压峰值，随测点沿柱高方向距离炸药越远这种差异越小.

取柱中轴线和柱两侧边缘的均值将其分成3部分进行第1次折线简化，见图9：柱两端为第1部分，超压荷载峰值呈非线性分布有明显的拐点，但因荷载较小且离支座端较近对柱子的动力响应影响较小故将其简化成一次线性分布；第2部为超压荷载过渡阶段，超压荷载峰值呈线性分布；第3部分超压荷载峰值分布较复杂但总体持平.

因ANSYS/LS-DYNA不能进行面荷载的梯度施加，所以将第1次简化后的折线荷载进行第2次简化：第1、2部分遵循等冲量原则，取各部分荷载平均值作为该部分的荷载值施加在结构表面，第3部分为结构主要破坏区域，为保证计算结果的安全性采取包络原则，取荷载最大值作为该部分的荷载值施加在结构表面. 简化后的对应冲量(I)见图10、11.

3 近爆作用下钢筋混凝土柱动力响应及损伤数值分析方法对比

3.1 LS-DYNA数值模型建立

为研究不同加载方式对近爆作用下钢筋混凝土柱动力反应及损伤破坏的影响，本文根据之前所述试验分别建立荷载简化模型、blast-load计算模型、流固耦合3种钢筋混凝土柱动力响应计算模型(由于炸药在对称位置摆放，考虑模型对称性，使用对称模型建模以提高计算效率)，材料参数可见表1.

混凝土采用072_R3损伤本构模型. 其包括初始屈服面、极限强度面和残余强度面，可以较好模拟各阶段变化. 该材料还可以通过动力增大系数DIF(材料动强度与其静态强度之比)来考虑应变率效应. 本文采用MALVAR等[12]提出的应变率增大系数，计算规定如下.

表1 材料参数

1) 混凝土受压

(3)

(4)

2) 混凝土受拉

(5)

(6)

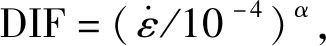
计算时要考虑静载和动载联合作用问题，需要先施加轴力，待轴力稳定后再施加爆炸荷载，见图13，其中，O～T1为轴压荷载准静态加载时间；T1～T2为轴压荷载稳定时间；T2～T3为爆炸荷载加载时间. 3种加载方式的模式如下：

① 流固耦合模型

由炸药、空气、柱、支座组成，见图14，同2.1节,炸药用JWL方程模拟爆炸压力，见式(2)；空气采用空材料和EOS状态方程模拟. 模型中采用侵蚀算法处理可以删除变形过大的Lagrange混凝土单元，从而保证计算的精度和效率，以及计算的正常运行. 师燕超[3]提到在流固耦合中网格尺寸对爆炸荷载有影响，为了提高计算时间且保证计算的精度，在炸药所在的主要受载核心区采用1 cm的网格，在非核心区采用1～5 cm渐变网格.

② 荷载简化模型

由柱、支座组成，混凝土材料、钢筋材料采用前述本构，爆炸荷载由简化后的荷载分段施加在柱表面，见图15.

③ Blast-load计算模型

由柱、支座组成，见图16，混凝土材料、钢筋材料同荷载简化模型，在其K文件中设置*LOAD_BLAST卡片，其炸药当量设为7.6 kg，并设置炸药中心坐标.

以上3种模型中都建立了支座，其采用固定的刚体材料，柱与支座之间采用弹簧单元1e-4和阻尼单元0.2模拟试验中支座与试件之间的橡胶垫块. 柱中钢筋和混凝土分离式建模，钢筋与混凝土之间采用共节点方式连接，在误差允许的范围内极大减少了计算时间提高计算效率.

3.2 结果对比分析

采用不同爆炸荷载加载方法的计算结果见图17和表2，在柱子的1/4位置，3种分析模型的最大位移结构相差不大，但荷载简化的震动周期最短，震动回弹相对较弱，残余位移模拟较好；流固耦合的震动周期中等，震动回弹和残余位移模拟较好；Load blast的震动周期最长，震动回弹较好，但残余位移较大，因为Load blast基于无限平面假定，不能考虑柱子的绕射作用. 如表3所示，荷载简化、Load blast的所占内存、计算时间较少，计算效率较高. 流固耦合所占内存、计算时间较大，但误差较小，比较适合精细模拟. 采用流固耦合加载时钢筋混凝土柱的跨中位置的位移最大值是3种加载方式中最高的，其次是荷载简化，二者的残余位移相似；采用Load blast加载时，钢筋混凝土柱的残余位移是3种加载方式中最大的，跨中位置最大位移却是最小的.

表2 实测值与计算值对比表

表3 误差及计算效率对比表

图18为试验破坏图，对比图19可知，3种模型都可以较好地模拟钢筋混凝土柱的破坏形式，Load blast产生的损伤与试验拟合最好，流固耦合因为采用侵蚀算法处理所以删掉部分单元，流固耦合模拟爆炸过程中不考虑外界干扰为理想化模型，模拟过程中引起流场在柱表面复杂的反射与叠加，支座处的荷载相对试验消散较小，简化模型在流固耦合的基础上为了简化而增大了支座处的荷载. 所以采用荷载简化与流固耦合的加载方式都在支座处产生了轻微受压破坏，其中简化模型加载产生的受压破坏程度更高.

4 结论

1) 荷载简化方法、Load blast、流固耦合3种模型都可以较好地分析近爆作用下钢筋混凝土柱的动力响应及损伤破坏.

2) 采用本文提出的简化荷载加载方式，其计算位移误差较小且所占内存较小，但造成结构的震动周期相对较短且需要掌握2种软件多次建模；采用Load blast命令加载方式建模简单、计算时间较短、所占内存较小、模型稳定不易出现结构网格畸变、荷载造成结构的震动周期拟合较好但残余位移误差较大；采用 “炸药- 空气- 混凝土柱”流固耦合加载方式建模较为复杂、计算时间较长、所占内存较大、运算时需要采用侵蚀算法以免结构网格畸变，但误差较小.

3) Load blast计算模型损伤模拟较好，修改炸药比例距离方便，适用于试验前不同炸药比例距离下构件损伤预估；流固耦合模型计算误差较小，适用于试验的拟合；荷载简化方法模型，计算效率高、误差小，适用于构件抗爆试验后的参数分析. 科研人员可以根据不同的需要参考本文选择不同的模型进行计算分析.