基于图像质量分析的PM2.5空气质量预测

李晓理，张 山，王 康,2

(1.北京工业大学信息学部，北京 100124； 2.计算智能与智能系统北京市重点实验室，北京 100124；3.数字社区教育部工程研究中心，北京 100124； 4.北京未来网络科技高精尖创新中心，北京 100124)

近年来，城市化规模不断扩张,工业的发展和化石燃料的消费也有所增加，导致了中国空气污染的增加，许多城市出现了水、空气和噪声污染等严重的环境污染问题. 与使用有效的方法处理水和噪声污染问题相比,目前,人们却对最常见的空气污染没有更简单、便捷的办法，这使得环境可持续发展的目标难以实现. PM2.5是由具有高活性的有毒有害物质组成，并且在大气中显示出长的停留时间和远距离的运输距离. 据报道，暴露于高质量浓度的PM2.5会导致心血管和肺部疾病的增加，对健康特别有害，每年导致约700万人死亡[1-4]. 当其含量超过环境承载能力时，空气质量将会恶化，导致人们的工作、生活、健康以及生态环境等遭受严重破坏. 此外，空气污染的许多来源并不能得到有效控制，而且这些来源的数量不断增加. 如上所述，在短时间内彻底治理空气污染问题是很困难的. 因此，大多数人逐渐重视大气污染物质量浓度预测和大气污染预防措施. 此外，迫切需要一种用于监测空气质量的有效且经济的方法，促进环境部门做出决策，例如实时向所有用户发布空气质量信息，并且他们可以提前采取预防措施.

目前，在空气污染预测应用中有各种机器学习算法. 陈淳祺等[5]应用多元线性回归模型研究武汉市气象环境对空气质量的影响和相关性. 白鹤鸣等[6]用神经网络算法预测空气质量指数. Liu等[7]使用反向传播神经网络和选择样本规则来预测城市空气质量. 李翔[8]将遗传算法优化的误差反向传播网络(back propagation neural network，BPNN)和模糊BPNN应用于空气质量预测. Sun等[9]用隐马尔可夫模型算法预测北加利福尼亚州的PM2.5质量浓度. 最近，Zhou等[10]利用混合集合经验模式分解和广义回归神经网络对PM2.5质量浓度进行预测. 当然，使用组合的方法能得到更好的预测结果，但是这些方法的弊端也是显而易见的，如运行时间长、成本高等.

众所周知，图像在记录信息、传达思想和表达日常生活中的情感方面发挥着越来越重要的作用. 因此，本研究不同于以往单一的利用机器学习的方法，仅结合污染物质量浓度数据和气象数据对污染物质量浓度进行预测，而是考虑空气污染会影响图像的质量，从图像质量分析的角度，结合机器学习方法对污染物质量浓度进行预测，目的是进一步提高PM2.5质量浓度预测的准确性.

1 特征提取

1.1 图像质量分析

与好的天气相比，在恶劣天气下拍摄的照片往往更为有序. 这一现象主要是因为饱和度可以看作是一种颜色与其最接近的自然光谱颜色之间的相似性，当PM2.5质量浓度较大时，颜色特征参数会降低到一个很低的水平. 在这种情况下，图像中每个像素的饱和度往往变成零，整个空间饱和度趋于稳定和有序. 也就是说，雾霾天气改变了图像的对比度和自然统计特性，这反过来又影响图像的质量. 图1很形象地说明了上述现象. 仅相差半个小时，就可以直观地感受到雾霾天气给图像带来的明显改变. 由此可知，直观上不同颗粒质量浓度的霾会影响图像的视觉效果. 实质上是因为图像的自然特性和对比度发生了变化. 因此，本文选择与上述2种特性相关的图像质量评价模型进行特征提取.

1.2 特征提取

本研究首先获取日常天气照片，得到大量的图像数据集. 通过图像质量评价(image quality assessment，IQA)的方法，获取相应的特征. 目前，现有的特定的盲测量方法受到失真类别的先验知识和专用应用场景的依赖性的极大限制，导致可以同时处理各种失真类型的通用型无参考(no reference, NR)IQA引起了更多关注，因而，有许多质量度量被提出用来测量原始图像和失真图像之间的差异/保真度以预测质量评分. 本文选择了3种最新的图像质量评价模型(无参考的基于自由能的鲁棒测量模型、使用图像直方图的相位一致性和统计信息来呈现用于对比度变化的模型和无参考调频质量指数模型)来提取特征.

1.2.1 第1组特征

第1组特征是利用文献[11]中所用的模型进行提取的，它根据所提出的一种NRIQA度量，称作无参考的基于自由能的鲁棒测量，使用最近揭示的基于自由能的大脑理论和经典人类视觉系统(human visual system, HVS)原理来提取特征[12]. 这组特征又可以分为如下3个部分.

第1部分涉及受自由能原理和结构退化模型启发的特征. 该特征来自2个有效的全参考IQA算法及其组合. 本文算法是根据自由能理论实现的，正如Friston揭示的自由能理论，将生物和自然科学中关于人类行为、感知和学习的几种脑理论的解释统一起来. 类似于贝叶斯脑假说[13]，基于自由能的脑理论的基本前提是认知过程，是由内部生成模型操纵的. 使用这种生成模型，人类大脑可以主动推断输入视觉信号的有意义信息的预测，并以建设性的方式避免剩余的不确定性. 这个建设性模型是一个基本的概率模型，可以将其分解为可能性项和先验项. 然后，视觉感知通过反转这个可能性项来推断给定场景的后验可能性. 在真实场景和大脑预测之间存在差距是自然的，因为生成模型不可能是通用的. 外部输入与生成模型预测结果产生的偏差被认为与人类视觉感知的质量密切相关，甚至可以用于质量测量.

第2部分特征是由一些HVS启发的特征(例如结构信息和梯度)预测图像的特征组成，也受到自由能理论的启发，这说明HVS总是试图通过减少基于内部生成模型的不确定性来感知和理解输入视觉刺激.

第3部分特征通过将广义高斯分布(generalized Gauss distribution, GGD)拟合平均减去对比归一化系数来量化失真图像中“自然度”的可能损失. 在文献[14]中，发现解相关函数可以通过应用局部非线性运算来对比亮度，以消除零对数对比中的局部平均位移并归一化对数对比度的局部变化. 此外，这些归一化的亮度值使自然图像的高度趋近于单位正态高斯分布，该方法已被用于模拟早期人类视觉中的对比度增益掩蔽过程. 因此，可用GGD来有效捕捉失真图像的更宽泛的统计量，根据公式

(1)

估计均值为零的GGD. 式中

(2)

(3)

式中，参数μ控制着分布的形状，而另一个参数σ2则表示分布的方差. 在本研究中，选择局部归一化亮度系数的分布是由于其通常是对称的，所以选择零均值分布. 通过部署这个参数模型来拟合扭曲图像以及未失真图像的局部归一化亮度系数经验分布. 对于每幅图像，首先估算2个参数(μ,σ2),这2个参数分别通过对原始尺度进行局部归一化亮度参数的GGD拟合及使用低通滤波方法降低图像分辨率的处理方法得到；然后进行2倍因子下采样，构成最后一组特征；最后，通过这个模型共提取了750×19组特征.

1.2.2 第2组特征

第2组特征是根据文献[15]中所用的模型进行提取的. 目前，IQA的研究主要集中在噪声、模糊、传输误差和压缩图像方面. 通常，失真图像的感知质量低于其相应的理想版本. 然而，对比度变化与上述失真类型不同. 为了填补这个空白，本文使用图像直方图的相位一致性和统计信息来呈现用于对比度变化的图像质量度量.

该模型通过两阶段框架来描述图像对比度变化的IQA[16]. 第1个阶段是比较原始图像和对比度变化图像的相似性，因为高质量图像应该与其原始副本很相似. 此外，人们通常关注显著区域，因此，用相位一致性原则(phase congruence, PC)搜索重要区域，然后估计原始图像和对比度变化图像中所选区域的熵差异. 第2个阶段与“舒适度”有关. 在这个框架中采用一阶、二阶统计量(均值和方差)，根据它们在图像质量评估中的贡献分别设为20和25. 另外，在神经科学和自然场景统计中经常使用第3和第4阶统计量(偏度和峰度)，其揭示了高阶统计量与人的舒适感有关.

1) 相似性

熵作为统计学中的一个主要概念[17]，它通过量化其平均不可预测性来表示随机信号的信息量. 高对比度图像的熵通常较大. 首先将对比度变化图像x的熵表示为

(4)

尽管熵能够测量图像信号的平均不可预测性，但它不能表征和区分各种图像场景. 例如，虽然可以很容易地找出2个具有相同直方图和熵的图像，但它们分别呈现出美丽的景象和无序的图像. 因此，通过计算原始图像和对比度变化图像的选择性熵值的差异以测量相似度. 对于原始图像s，基于PC的熵也被类似地定义为Hs(y)，然后用相似度量化.

R0=Hs(x)-Hs(y)

(5)

2) 舒适性

原始图像y的平均值或一阶统计量决定了图像直方图的整体亮度. 在照相技术中，一对经常遇到的问题是曝光过度(高平均亮度)和曝光不足(低平均亮度)，这经常会降低照片的质量并降低用户的舒适度. 因此，摄像机通常具有自动调节图像直方图的功能，可以使用适当的Gamma传输. 但与此同时，不正确的Gamma功能选择将恶化图像对比度和视觉质量. 因此，通过引入一个高斯核函数

R=exp [-((E(x)-α)/τ)2]

(6)

来设计一阶统计相关项，从而惩罚具有非常大或较小平均值的图像.

其中E(x)被定义为图像x的期望值，并且α和τ是确定使用的高斯核的均值和形状的固定模型参数. 最后，将相似度和舒适度结合起来，得出对比度变化图像的整体质量分数. 最终，使用简单的线性融合来整合基于PC的熵和四阶统计的差异. 值得注意的是，此类模型只需要一个单一的数字，即原始图像Hs(y)基于的PC熵与图像文件的大小相比通常可忽略不计，只需在头文件中进行编码即可. 鉴于此，最终得到750×4组特征.

1.2.3 第3组特征

第3组特征是根据文献[18]中所用的无参考调频质量指数模型进行提取的. 由于动态范围的限制，色调映射图像不能保留原始图像的所有信息. 首先假设一张好的色调映射图像包含大量信息是合理的，然后在此基础上，评估色调映射图像质量的第1个考虑因素是直接估算其本身的信息量以及通过使原始亮度变暗/增亮所产生的中间图像. 接下来，再寻求一种衡量信息量的方法，常用的如Kullback-Leibler散度及其修正的对称格式. 通过实验发现，散度的发散或其对称版本的使用不能有助于性能增益的显著提高，相反会引入很多成本时间，因此，决定用熵[17]来量化信息量.

另外,考虑的第2点是图像的统计自然性. 首先假设高质量的色调映射图像也应该看起来很自然. 在过去的几年中，为了促进图像/视频处理技术的探索和对生物视觉的理解，有大量的文献倾向自然图像的统计[19]. 许多现有的NRIQA度量标准都是基于自然场景统计的[20]. 这些模型背后的基本思想在于，自然图像通过局部平均去除和分裂归一化处理，使归一化系数严格地遵循高斯分布，不同的失真类型或级别的图像将重新形成此分布.

然而，上述统计模型在评估色调映射图像的视觉质量方面并不合适，因此，需要另一种基于自然统计特性的模型. 对色调映射图像进行自然统计的研究表明，自然度和图像属性存在高度相关性，特别是亮度和对比度[21]. 因此，所用的模型考虑了根据平均亮度和对比度形成的统计自然度模型[22]. 基本上，这个模型在捕捉自然图像的关键因素的简单性和能力之间达到平衡.

第3点考虑的是校准色调映射图像保留主要结构的能力. 在文献[23]中，Wang等表明HVS高度适应从输入视觉刺激中提取结构信息，并且他们还提供了大量示例来证明基于结构相似性指数在评估图像质量方面优于传统的均方误差. 事实上，许多高精度的IQA算法是基于结构相似性[24]或梯度幅度相似性设计的，可以将其视为图像结构的另一种度量[25]. 最终，从色调映射图像中提取了共750×11个特征.

2 质量浓度预测

2.1 实验原理

在特征提取之后，需要使用回归模块找到从特征空间到主观平均意见分(mean opinion score，MOS)的合适映射，产生图像质量的度量. 根据预测模型与原始图像数据之间的残差，找到与PM2.5质量浓度之间的联系，用非线性映射的方法估计PM2.5质量浓度的自然可能性.

在实验中，将支持向量回归机(support vector regression, SVR)[26]应用于图像质量评估问题[12]. 首先，利用具有径向基函数(radial basis function, RBF)内核的SVR做了一个简单的实验. 随后，为了展示提取特征的有效性并与最先进的技术进行比较，本文利用粒子群优化的支持向量回归机(support vector regression for particle swarm optimization，PSO-SVR)和用遗传算法优化的支持向量回归机(support vector regression for genetic algorithm，GA-SVR)预测PM2.5质量浓度. 最终的实验结果证实了PSO-SVR预测模型的优越性. 利用粒子群算法对SVR参数进行优化的整体算法过程如图2所示.

2.2 参数的选取与优化

核函数是支持向量机的重要组成部分，通过把数据映射到高维特征空间来增加传统的线性学习器的计算能力. 核函数的构造及其相应参数的选取都能对SVR的性能造成一定的影响，因此，要想提高预测精度必须选择合适的核函数和相应参数. SVR模型有2个非常重要的参数c与g，其中c是惩罚系数，即对误差的宽容度.c越高，说明越不能容忍出现误差,容易过拟合；c越小，容易欠拟合.g是将RBF函数作为核函数后该函数自带的一个参数,间接地决定了数据映射到新的特征空间后的分布，g越大，支持向量越少；g越小，支持向量越多. 支持向量的个数影响训练与预测的速度.

本文选择使用2种启发式算法来查找SVR核函数的c和g. 首先，当进行第1个简单的实验时，将上述2个参数在一定范围内取值，最终取性能最好的值. 其次，先用第1种元启发式算法- 遗传算法(genetic algorithm，GA)对2个参数进行优化. 最后，再用PSO算法进行优化. 由于PSO是一种基于群体智能的进化计算技术，与GA相比，PSO没有选择、交叉、变异操作，而是在可行域中搜索跟随的最佳粒子. 目前，该算法已在多领域有广泛的应用[27]. 基于PSO算法的函数极值寻优算法的流程图如图3所示. 本实验中，适应度函数是Ackley函数表达式，适应度值为函数值. 种群粒子数为20，每个粒子的位数为2，算法迭代进化次数为100.

对于一组图片，整体可能性越大，PM2.5质量浓度越小. 因此,需要一个非线性映射来将残差值转换为最终的PM2.5质量浓度. 鉴于此，需要采用非线性映射来提高性能的准确性，但不影响输入数据的单调性. 因此，本文选择最简单的三参数非线性函数

(7)

式中{λ1,…,λ2}是在曲线拟合过程中确定的自由参数.

3 实验与结果分析

3.1 实验内容

3.1.1 数据获取与处理

为了评估基于图像分析的PM2.5质量浓度的预测能力和准确性，建立一个数据库是至关重要的. 在目前的工作中，选择文献[28]中使用的空气质量图像数据库作为测试平台进行验证. 该数据库包含了过去3年不同PM2.5质量浓度下相机拍摄的750张照片. 涉及公园、湖泊、公路、建筑物等多个场景，这样可以近似表征自然场景中的空气质量分布. 这些照片的分辨率从500×261到978×550. 每幅照片的相关PM2.5质量浓度由美国驻北京大使馆提供的每小时PM2.5质量浓度历史数据以及参考安装在北京工业大学校园内的监测设备获取，以做比较与分析. 本文选择2个设备及记录数据界面，如图4、5所示. 为了确保图像的质量，图像的采集须有一定的前提条件，首先是要在无风或有微风的天气拍摄，这样可以最大限度地保证获取到的图像所对应的PM2.5质量浓度与监测点报告的真实PM2.5质量浓度接近. 其次是,捕获的图像必须包含天空,大约占1/3～1/2图像的区域,并避免面对太阳. 在整个数据集中，PM2.5质量浓度为1～423 g/m3(值越低，表示空气质量越好).

同时，由于光线的散射作用，天空在晴朗的日子是蓝色的，在朦胧或阴天的时候，天空是灰色的或白色的. 天空中云的存在可以直接从图像中检测出来，用来区分它和朦胧的天空. 通过结合色彩和光滑的特点，试图确定清晰、部分阴天、阴天和朦胧的日子. 这些信息结合在线天气数据可帮助最大限度地减少对天气条件判断的误差.

3.1.2 实验过程

首先，获取图片数据，根据2节提及的模型与方法进行特征提取，分别得到750×19、750×4、750×11三组特征；其次，针对SVR、GA-SVR、PSO-SVR回归模型预测方法，分别按训练集和测试集的比例7∶3、8∶2、9∶1进行3组实验，共9组实验，用来比较各个实验的结果与模型性能. 同时，验证预测数据与实际数据的相关性，具体的结果见表1.

3.2 结果分析

为验证所提出的PSO-SVR模型的高效性，将实验结果与一般的SVR和GA-SVR模型进行比较. 相关性分析的图表可反映2个变量之间的相互关系及其相关方向，但无法确切地表明2个变量之间相关的程度. 于是，实验选择了利用计算相关系数以反映变量之间相关关系的密切程度. 引入了性能指标皮尔逊相关系数来评估模拟结果，计算公式为

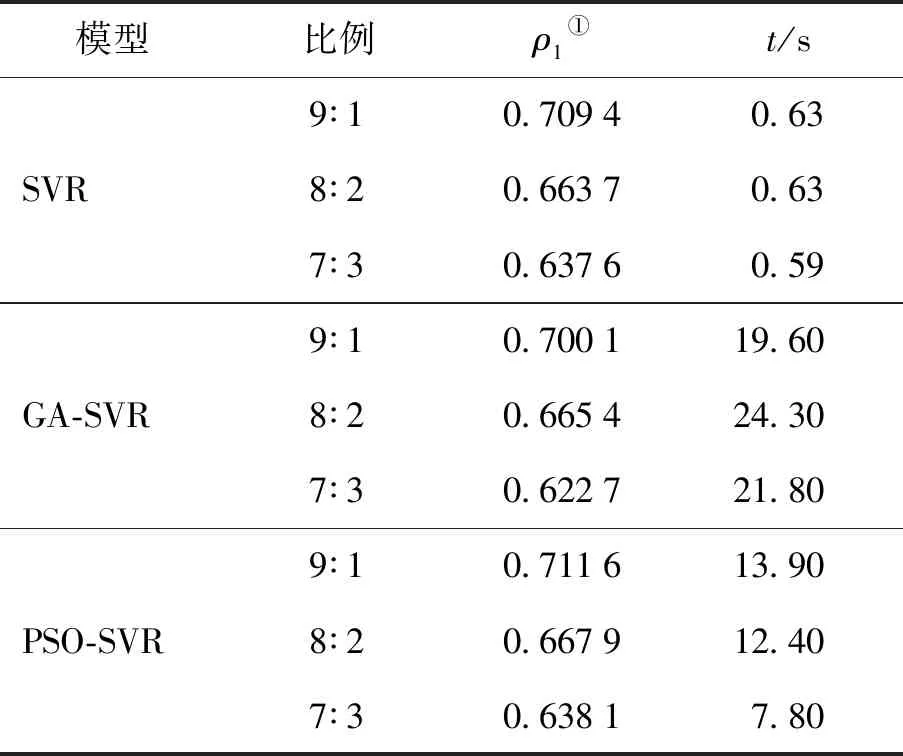
表1 3种模型的数值性能和运行时间的比较

①ρ1为皮尔逊相关系数.

(8)

从表1可以看出，随着训练集和测试集的比例从7∶3变到9∶1，3种模型的整体性能均逐渐变好. 当训练与测试数据比例设置为9∶1时，3个模型的性能由好到坏依次为：PSO-SVR、SVR、GA-SVR；当训练与测试数据比例设置为4∶1时，依次为PSO-SVR、GA-SVR、SVR；当训练与测试数据比例设置为7∶3时，依次为PSO-SVR、SVR、GA-SVR. 虽然PSO-SVR的执行时间相对较长，但由于计时时间单位是s，并不会受太大影响. 总体来说，PSO-SVR的性能始终表现最好. 虽然在运行时间上并不是很占优势，但通过增加数据集，可让模型在时间方面做进一步验证.

4 结论

1) 考虑到雾霾天气图像的对比度和自然统计特性发生显著变化，本文基于图片数据，结合图像分析技术对PM2.5质量浓度进行预测. 所研究的方向在领域内具有一定的代表性.

2) 获取不同天气、不同场景和不同时间的图像数据，参考多种已经建立的图像质量评估模型，提取关于空间域和变换域的熵等多组特征. 本实验选择了3个模型进行特征提取.

3) 利用熵特征和统计模型之间的关系寻找与PM2.5质量浓度之间的相对关系，得出反映给定图像PM2.5质量浓度的可能性的相对值.

4) 使用简单的非线性逻辑函数将可能性测量映射到估计PM2.5质量浓度. 最终结果验证了本文模型在数值方面获得了所有模型中最好的性能，且具有计算成本低和实现效率高的优点.

5) 本文设计了一个简单且依赖于经验的方案，而其他的基于机器学习的先进技术将会在以后进一步进行研究.