基于灰色神经网络的航线客流量预测

徐 涛 孙媛媛 卢 敏

1(中国民航大学计算机科学与技术学院 天津 300300)2(中国民航信息技术科研基地 天津 300300)3(民航旅客服务智能化应用技术重点实验室 北京 101318)

0 引 言

近年来，随着旅客出行需求的逐步增长，越来越多人选择飞机出行。实现航线客流量的准确预测，对航空公司而言，无论是对运力安排、市场拓展、未来发展等作出重要决策，还是制定航班计划和机队规划都是必不可少的[1]。

国内外关于航线客流量预测研究从早期的统计模型和计量经济学模型到现阶段的时间序列模型[2]、神经网络模型[3]、支持向量机模型[4]以及组合模型[5]等。这些模型大都只是基于旅客订票历史数据进行预测，鲜见考虑民航旅客出行的随机性及航线旅客流量的非线性特征。由于民航行业的特殊性，较难准确获取旅客在航线上的具体信息，因而对客流量预测影响较大的因素(如折扣、机型、舱位等)与客流量之间的关系分析不足。

综上，现有对航线客流量的研究存在以下问题：(1) 鲜见对航线客流量数据特征作准确分析，根据数据特征选用合适模型进行预测；(2) 缺乏对航线客流量影响较大因素的分析，影响预测精度。

针对上述问题，本文对航线客流量数据的非线性及随机性进行分析，同时验证平均折扣率对航线客流量的影响。运用灰色理论弱化航线客流量数据的随机性，再结合非线性处理能力较强的BP神经网络，构建灰色神经网络模型对航线的客流量进行预测，避免了选用模型的盲目性以及对客流量影响较大因素的疏忽。

1 数据来源及特征分析

1.1 数据来源

本文的数据来源是中国民航旅客订票记录(Passenger Name Record，PNR)，旅客的一次出行记录为一条信息，记录中包含旅客订票的航班、舱位、折扣等重要属性。数据集中属性含义如下：

身份证号：为保护旅客个人隐私，根据真实身份证号通过加密算法进行处理。

航空公司：为保护航空公司的隐私，航空公司的名称采用数字代号表示。

航班号：由真实航班号信息进行填充，用于区分不同航班信息。

起飞日期：表示旅客具体出行时间(年月日)，出于对旅客出行信息的保护，年份采用201X表示。

起飞机场、目的机场：采用国际航空运输协会规定的机场“三字码”表示。

舱位：区分旅客出行的舱位等级。如：F舱表示头等舱，C舱表示商务舱，Y舱表示经济舱，W舱表示折扣普通舱。

折扣：表示旅客购买机票时的折扣信息。

数据示例如表1所示。

表1 PNR数据示例

选取201X年及次年某航空公司每天北京飞三亚航线的旅客流量、折扣等指标作为本文研究的对象。

1.2 数据预处理

将数据进行整合分析，以天为单位统计北京飞三亚航线的旅客流量、平均折扣率，记Ys为该航线第s天的旅客流量：

(1)

式中：m表示该航线的航班数；nj表示该航线第j个航班的旅客人数。

不同航班不同舱位对应折扣的含义不同，对含航班舱位等级的平均折扣率Diss计算如下：

(2)

式中：l表示该航线有l种舱位；zjk表示乘坐第j个航班第k种舱位的旅客人数；Pjk表示第j个航班上第k种舱位的价格(根据航空公司、航班号及舱位结合现有订票软件统计得到各个舱位的价格)；Gjki表示第i位旅客在第j个航班上乘坐第k种舱位的折扣。

根据式(1)-式(2)，可以得到北京飞三亚航线的旅客流量、平均折扣率等指标数据。

1.3 数据特征分析

航空客流量受不同因素影响，通常表现出不同的变化特征[6]。对航空公司航线客流量进行建模首先要对航线客流量的数据特征进行分析，根据表现出的特征构建合适的模型进行预测。

根据北京飞三亚航线客流量的分布特征，淡旺季区分较明显，每年的十月至次年的四月三亚气候适宜，这段时间客流量明显高于其他月份。淡季客流量变化相对平稳，本文主要针对该航线旺季(201X年十月下旬至次年三月下旬)进行分析预测，航线客流量通常表现出很强的非平稳非线性特征。

首先，对航线客流量序列进行单位根检验以验证序列是否平稳以及对序列的自相关性进行分析，验证序列的非线性特征。据表2航线客流量序列的单位根检验可知，概率值(P值)大于10%，不能拒绝原始假设，因此序列为非平稳序列[7]，说明民航旅客订票随机性较强。

表2 航线客流量序列的单位根检验

其次，对航线客流量序列进行一阶差分并进行单位根检验，由表3检验结果知，序列一阶差分后概率值(P值)小于10%，证明差分后的序列已平稳。且表3中自相关、偏相关图与右边自相关系数与偏相关系数相关，“*”代表其超出置信空间，而“·”代表在置信空间内。通过对一阶差分后的序列进行自相关、偏相关分析后发现，自相关系数和偏相关系数三阶后快速收敛于置信区间内，故存在三阶截尾，所以对差分后的序列建立自回归积分滑动平均模型ARIMA(3,3,1)。

表3 一阶差分序列的相关性检验

最后，对序列残差以及残差的平方进行自相关分析(见表4、表5)，自相关系数与零存在显著的差异，说明序列残差及残差的平方均存在自相关性。因此，航线客流量序列具有非线性特征。

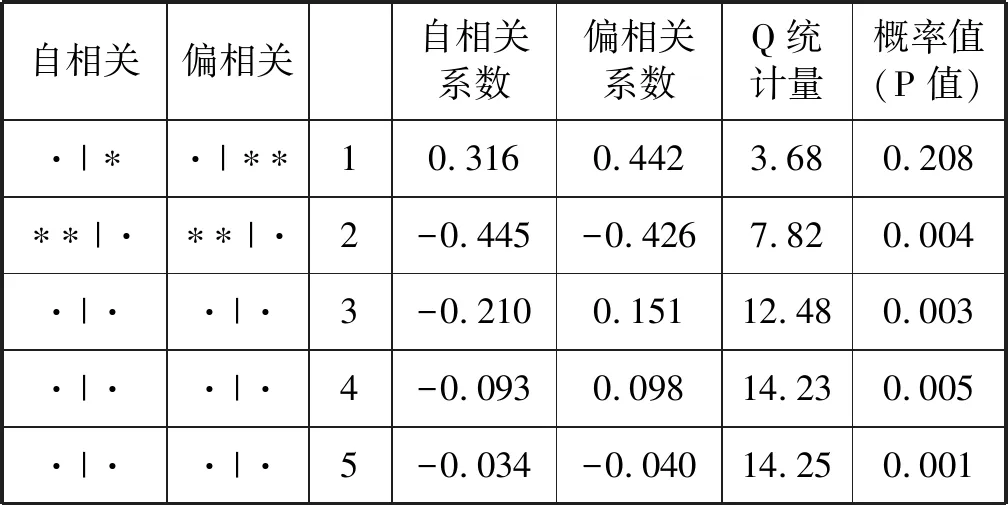
表4 序列残差的相关性检验

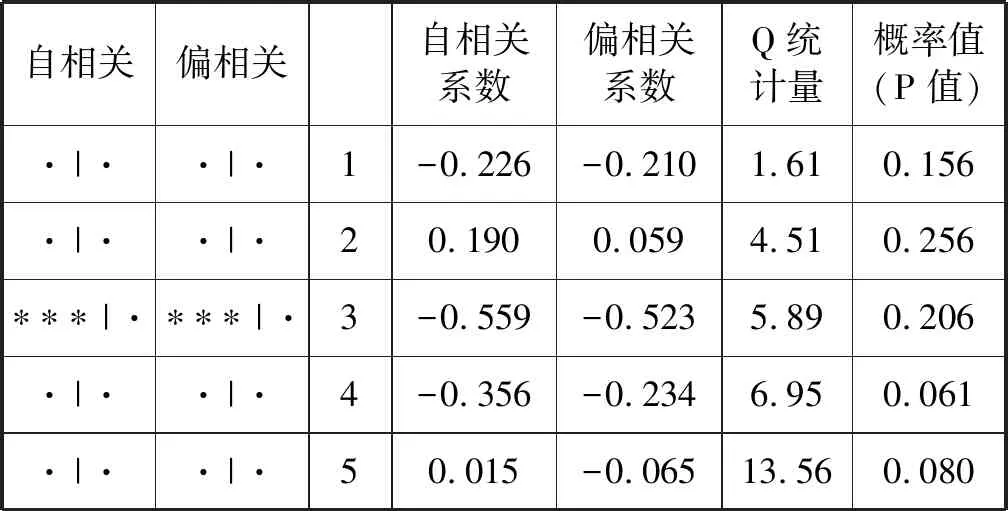
表5 序列残差平方的相关性检验

1.4 客流量与平均折扣率的相关性分析

式(2)平均折扣率的计算中包含了旅客订票的航班以及舱位等信息，故将平均折扣率作为航线客流量的影响因素较为全面。两者相关性通过相关系数进行分析。

相关系数是反映变量之间密切程度的一种统计指标[8]，它的主要目的是分析两个或多个变量之间的相关程度。1代表两个变量完全正相关，0代表两个变量不相关，-1代表两个变量完全负相关。对航线客流量Ys和平均折扣率Diss建立相关系数表进行相关性分析。由表6可知，航线客流量Ys与平均折扣率Diss的相关性系数为-0.667 91，说明这两个变量呈负相关关系。平均折扣率降低意味着折扣力度增大，旅客会更偏向于乘坐该航线，使得航线客流量增大。

表6 相关系数表

2 模型设计

2.1 航线客流量预测

航线客流量预测是具有不确定性的复杂系统，受许多因素的制约。灰色系统理论是一种处理“部分信息已知、部分信息未知”的“小样本、贫信息”不确定性的理论[9]，该理论认为通过生成变换可以将无规律的数据序列变成有规律的数据序列，弱化数据的随机性。通过1.3节对航线客流量数据的特征分析发现，航线上旅客流量具有随机性的特征，符合灰色理论的特点。并且航线客流量具有很强的非线性特征，BP神经网络具有较强非线性映射能力[10]，所以运用灰色系统理论和BP神经网络组合对航线客流量进行预测，具有较强的针对性。

2.2 灰色神经网络模型

灰色神经网络是在灰色系统理论中融入了神经网络的思想，通过网络反馈的形式不断地进行学习[11]。具体的算法流程如图1所示。

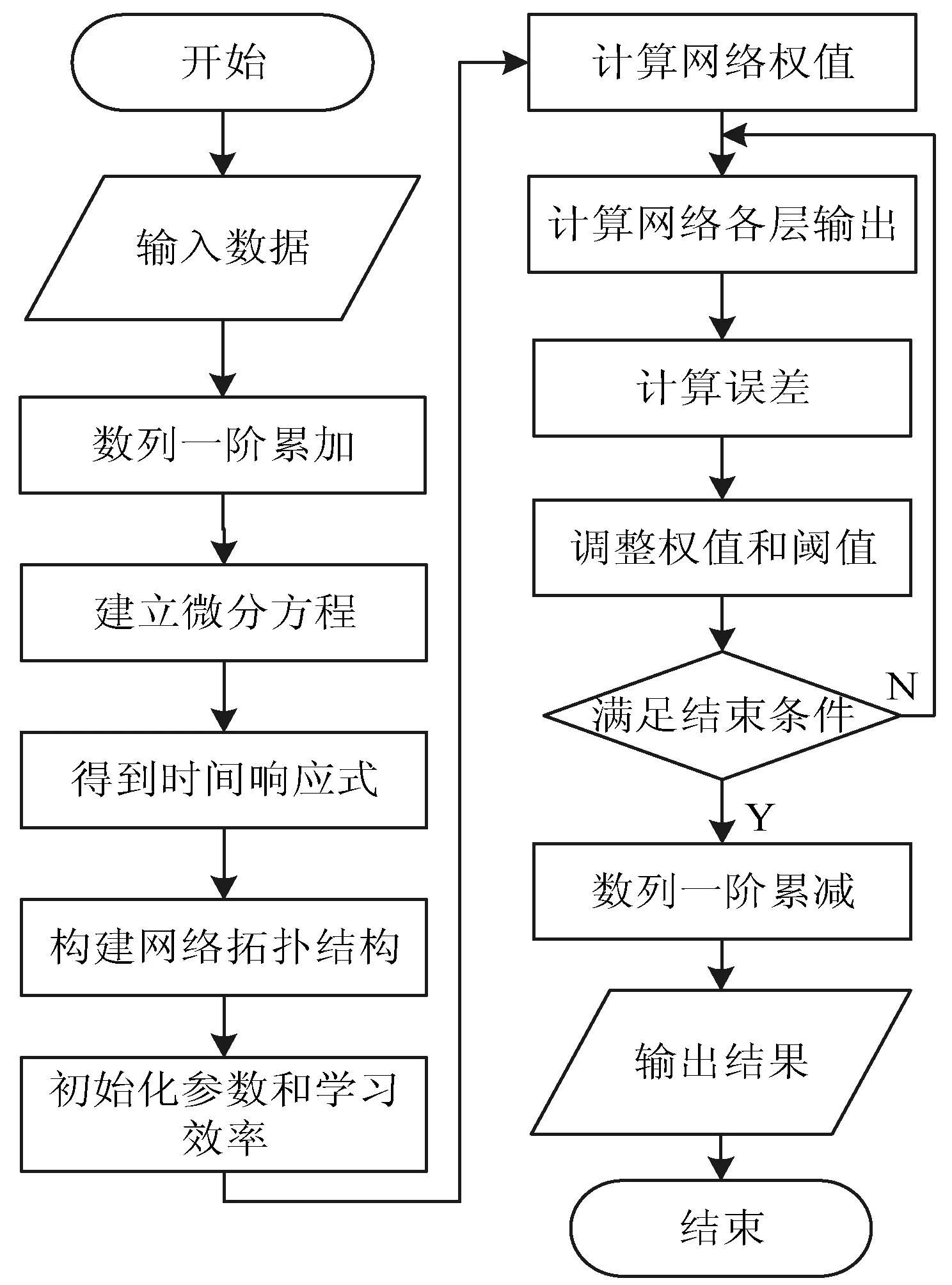
图1 灰色神经网络模型流程图

(3)

(4)

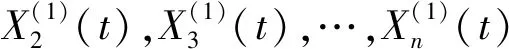
式(4)的时间响应式为:

(5)

令:

式(5)可作如下转化以映射到BP神经网络:

(6)

将变换后的式(6)映射到扩展的BP神经网络中，得到n-1个输入参数、1个输出参数的灰色神经网络，网络拓扑结构如图2所示。

图2 灰色神经网络拓扑结构

(7)

LD层输出节点的阈值为:

(8)

2.3 基于灰色神经网络的航线客流量预测模型

由航线客流量与平均折扣率的相关性分析可知，后者对前者存在较强的影响，故将平均折扣率作为影响因素加入航线客流量的预测。所以灰色神经网络结构为1-1-2-1，即LA层有1个节点，输入为时间序列t，LB层有1个节点，LC层有2个节点，第2个为平均折扣率，输出为航线客流量预测值，灰色神经网络的训练流程如下：

1) 网络初始化。根据训练数据特征确定网络拓扑结构，初始化参数a、b和学习速率μ。

2) 据式(7)计算网络权值ω。

3) 计算各层输出。对每一个输入序列(t,X(1)(t)),t=1,2,…,N，计算各层输出。

LA层：a=ω11t。

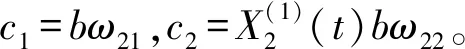
LD层：d=ω31c1+ω32c2-θ。

4) 计算误差。计算网络预测输出与期望输出的误差。

LC层误差：δ1=δ2=δ0(1+e-ω11t)。

5) 根据误差更新权值和阈值。

更新LA到LB的连接权值：ω11=ω11-atδ3。

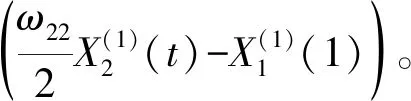
6) 判断训练是否结束，若没有结束，返回步骤3。

3 实 验

3.1 实验数据

以某航空公司北京飞三亚航线数据为例，该公司在本条航线上每日有4个班次，滤除订票后退票即没有实际乘坐的订票数。选取北京飞三亚航线201X年11月17日至次年1月17日(除元旦节假日)旅客流量及平均折扣率作为历史数据，对次年1月18日-1月31日航线客流量进行预测。

由于旅客订票数据量巨大，传统数据库进行操作速度缓慢，故航线客流量的统计通过搭建Hadoop伪分布式平台，采用Map-Reduce技术对大规模旅客订票数据进行处理，如图3所示。

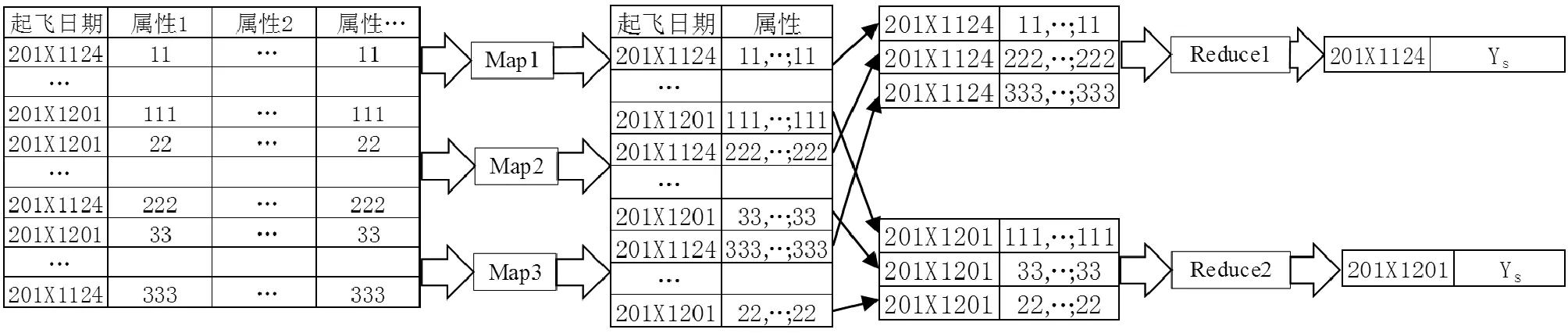
图3 Map-Reduce数据处理

通过采用Map-Reduce技术将数据处理集处理成北京-三亚航线上起飞日期-航线客流量记录文档的形式如表7所示。出于对数据的保密，对涉及到的航线客流量作了单位化处理。平均折扣率根据上面的计算得出，最终基于灰色神经网络的输入样例如表8所示。

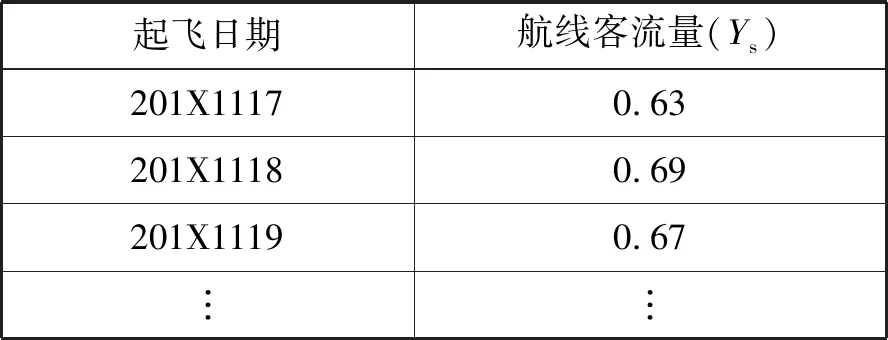
表7 日期-航线客流量记录文档

表8 基于灰色神经网络的输入样例

3.2 评价指标及参数设置

用预测客流量与真实的客流量的相对误差对实验结果进行评价。其计算公式如下：

(9)

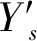
根据输入信息的特征以及期望输出，确定灰色神经网络的结构为1-1-2-1，因累加的数据具有单调增加的趋势，BP神经网络的非线性激活函数易逼近，故LB层神经元激活函数为Sigmoid型函数，其他层激活函数取线性函数。设置训练次数为100，学习速率u为0.001。

3.3 实验结果分析

为验证灰色神经网络模型在航线客流量预测方面的有效性，与灰色模型GM(Grey Model)、BP神经网络模型作对比实验。

根据上面的讨论，将平均折扣率作为影响因素加入到航线客流量预测中，建立灰色GM(1,2)模型和输入节点为2，输出节点为1的BP神经网络模型作对比实验，采用相同的航线客流量数据进行实验。图4给出了三种模型的客流量预测结果，以相对误差QRE为评价指标。

图4 北京-三亚航线客流量预测相对误差对比图

由图4可知，灰色GM(1,2)模型因结合航线客流量随机性的数据特征，预测相对误差较低，控制在7%以内，但预测稳定性较差，如在1月21日预测相对误差在3%左右，而1月30日预测相对误差却在6.5%左右。因BP神经网络模型结合航线客流量非线性的数据特征，预测相对误差较低，控制在6%以内，但预测稳定性也相对较差。

相比于BP神经网络模型和灰色GM(1,2)模型，灰色神经网络模型结合了航线客流量非线性和随机性的数据特征，预测相对误差更低，而且预测稳定性更高。同时平均相对误差(表9)比其他两种模型提高了1%左右，说明灰色神经网络模型更适用于航线客流量预测。

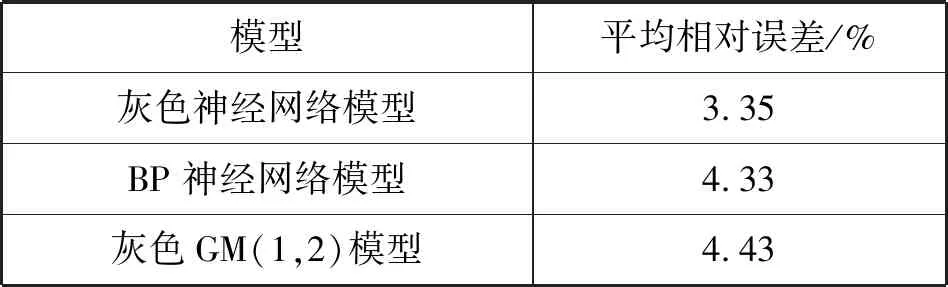
表9 模型对比

4 结 语

航线客流量预测对于提高航空公司收益有重要意义。本文对平均折扣率与航线客流量的相关性进行分析，结果表明，平均折扣率与航线客流量呈负相关关系，即随着平均折扣率的降低，折扣力度增大，旅客会更偏向于乘坐该航线，使得航线客流量增大。同时在对航线客流量数据特征分析的基础上，将弱化航线客流量数据随机性的灰色理论以及非线性处理能力强的BP神经网络模型组合为灰色神经网络模型对航线客流量数据进行预测。在相同数据集下的实验结果表明，针对航线客流量预测，灰色神经网络模型具有更高的预测准确率和更强的预测稳定性。