热模型下扬声器音圈温度的卡尔曼滤波预测
周静雷,董春君
(西安工程大学 电子信息学院,陕西 西安 710048)
0 引 言
热损坏与机械损坏扬声器单元的主要毁损方式有热损坏与机械损坏等2种。输入到扬声器的电能90%~95%被转化为热能,因此影响扬声器使用寿命的最主要原因是扬声器单元的热损坏。扬声器的热损坏常由音圈内部开始。作为扬声器最重要的零部件之一,音圈是将电能转换成振动的电动原件[1-2],音圈过热是扬声器损坏和故障的主要原因之一。
在音圈温度达到最大温度的前一时刻进行及时有效地控制(停止运行或调低功率等),是延长扬声器使用寿命的可行方法之一。卡尔曼滤波多数用于目标跟踪、运动轨迹预测、变形监测以及算法延迟补偿,大都分布在金融、交通、能源、无人机、自动驾驶等领域[3-6],将卡尔曼滤波用于预测扬声器音圈温度的情况极少,文献[7]提出了一种预测低频信号驱动下动圈式扬声器稳态温度场的数值分析方法,并通过自行设计的扬声器温度测量系统测量扬声器音圈及磁路外表面特殊点的稳态温度值;文献[8]运用卡尔曼滤波预测扬声器磁铁温度,将其作为热保护控制方案中的状态观测环节;文献[9]提出了基于传热模型的导线电阻温度系数的测量方法,这是扬声器热效应领域、温度测量技术中的一个重要参数。
本文基于卡尔曼滤波原理,实时预测扬声器下一时刻的音圈温度,利用卡尔曼滤波算法的参数估计功能,对音圈温度进行实时处理和超前预测,有助于在第一时间控制输入信号的功率,及时避免由音圈温度过高引起的扬声器热损坏,达到保护扬声器的目的。
1 回归预测算法
在环境温度23.2 ℃下,通过扬声器寿命试验仪测得音圈温度的实际温升数据,画出扬声器的音圈温度随时间升高的散点图,如图1所示。

图1 温升数据散点图
通过观测散点图可知扬声器的温升趋势与指数模型较为接近,根据温升模型特点,设回归模型为[10-11]

(1)
式中:y为试验测得的扬声器音圈温度;t为试验时间;a为指数回归常数;b,c为指数回归系数;τb为扬声器音圈温升常数;τm为扬声器磁铁温升常数。
2 扬声器热模型
扬声器在中频激励信号下,磁铁的涡流热效应和空气中的强迫对流效应均可忽略不计[12],此时扬声器的热传递模型如图2所示。

图2 扬声器中频段热模型电路类比图
图2中,Tc(t)为音圈温度,Tm(t)为磁铁温度,Ta(t)为环境温度,P(t)为热功率,Cb为音圈热容,Rb为音圈热阻,Cm为磁铁热容,Rm为磁铁热阻。
2.1 状态空间方程
根据电路类比图列出系统状态空间方程如下:

(2)

(3)
2.2 可观测性
在对系统运用卡尔曼滤波进行状态估计之前,系统需满足可观测性[13]。可观性矩阵表示为
(4)
音圈温度升高的稳定时间常数τb=RbCb,磁铁温度升高的稳定时间常数为τm=RmCm。
文献[14]表明,音圈温升时间常数小于磁铁温升时间常数,既τb<τm,满足rankUo=n(n为矩阵秩数)的要求,因此系统可观测。
3 卡尔曼滤波预测算法
1960年,Kalman于发表的论文中首次提出卡尔曼滤波的概念,利用2个正态分布的融合仍是正态分布这一特性进行自回归迭代,在不知道模型的确切性质的情况下,估计信号的将来状态[15]。
当实际测量同时存在模型预测和直接测量2种方式时, 由于预测噪声和测量噪声相互独立互不干扰, 需要对这2个结果进行一个可信度的取舍, 此取舍的权重系数称为卡尔曼增益。测量值和真实值的协方差最小时确定的系数就是卡尔曼增益系数。通过设定卡尔曼增益系数对估计值和测量值进行数据融合处理, 得到新的预估值并以此为根据更新卡尔曼增益系数, 使最终测量结果逼近真实值, 达到预测的目的[16]。
3.1 离散化
卡尔曼滤波将状态空间和最优滤波理论相结合,通过递推计算离散随机系统的状态估计值[17],连续状态空间模型的离散化方程可写成:

(5)
式中:T为离散化模型的采样周期。由连续系统离散化经典理论计算离散模型矩阵G(T),H(T):

(6)
3.2 滤波器设计


4 试验和仿真
寿命试验仪是一种对扬声器进行可靠性试验的仪器,能够在为扬声器提供激励信号的同时对扬声器的电压、电流及音圈的温度等特性参数进行测量。测量原理如图3所示。

图3 扬声器寿命试验仪音圈测量原理
寿命试验仪可以产生中频频段的激励信号对扬声器进行激励使音圈升温,通过扬声器寿命试验仪的音圈测温功能,得到音圈温度的实际测量值。
本次扬声器寿命试验在环境温度23.2 ℃下进行,激励信号为寿命试验仪产生的7 V,1 kHz的正弦信号,采样周期为0.1 s,选择额定阻抗8 Ω,额定功率10 W,室温下直流电阻为7.81 Ω的扬声器作为试验品。试验共分20组同时进行,每组试验取4 000个采样点,试验总时长为400 s。根据采样周期对数据进行均值处理,将其用于算法验证。用相对误差反映预测值的可信程度:
(7)
95%置信范围内的拟合结果为
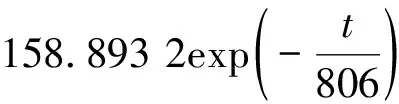
(8)
回归预测结果及相对误差如图4所示。从图4(a)可知,回归预测结果的拟合曲线与测量值基本吻合;从图4(b)可知,相对误差波动范围在0.273 7以内,100 s以后误差波动幅度减小,忽略异常点,整体波动范围在0.086 9以内。

(a)预测结果

(b)相对误差
卡尔曼滤波预测结果及相对误差如图5所示。从图5(a)可知,卡尔曼滤波预测结果与测量值吻合度很高,忽略初始时刻的异常点,从图5(b)可知,相对误差的波动范围在0.018 22以内,且波动幅度随着试验时间逐渐减小。50 s时刻的预测结果就较为精准,之后的误差波动范围稳定在0.013 29以内。选取[290,350]区间内的预测结果放大查看,可看出卡尔曼预测结果与实际测量值极其吻合。

(a)预测结果

(b)相对误差
抽取0 s,1 s,10 s,30 s,50 s,100 s,200 s,350 s时刻的音圈温度的回归预测值和卡尔曼预测值,与测量值进行对比,如表1所示。

表1 预测值与测量值的对比
图6为卡尔曼预测误差与回归预测误差比较。从图6可以看出,卡尔曼预测的值要比回归预测的更接近测量值,且误差范围稳定。
表2为卡尔曼预测与回归预测的相对误差值。从表2知,卡尔曼预测的相对误差的最大值最小值、平均误差与标准偏差均小于回归预测的相对误差。从图4图5对比可知,卡尔曼预测的误差值与误差波动范围均小于回归预测,说明卡尔曼预测具有更好的准确度和可靠度。

图6 预测值的误差对比

表2 相对误差值
5 结 语
针对扬声器音圈温度预测问题,对已采集的音圈温升数据进行均值处理,应用回归预测算法和卡尔曼预测算法,快速准确的预测扬声器音圈温度。回归预测算法是根据已知数据建立温升模型,直观地描述扬声器温度与时间的关系,具有更好的规律性;适用于试验环境、试验设备、激励信号、试验品等都相同的情况,因此机动性较差,不能根据测量值的突变进行及时的调整,但也避免了由异常数据引起的对预测值的过度矫正。卡尔曼预测模型则是运用卡尔曼滤波迭代算法预测音圈温度,适用于扬声器热模型已知的情况下;在出现异常点时,及时对卡尔曼增益值进行调整,使预测值靠近测量值,但也因此受测量值的影响较大,不能辨别异常并将其剔出,而使预测值的确定过于依赖测量值,从而在短时间内存在过度矫正的现象。综上所述,在相同的试验条件下,卡尔曼预测算法有更高的准确率与可靠性,且对突发情况的适应能力更强,因此最终选用卡尔曼预测算法作为扬声器音圈温度预测工具。

