基于模糊度参数估计的数字媒体图像无损复原
许靖添,冯 新
(1.北京师范大学珠海分校 设计学院,广东 珠海 519087;2.大连理工大学 建设工程学部,辽宁 大连 116024)
0 引 言
在实际生活中,模糊图像经常发生在监控设备及各种摄像设备拍摄过程中。造成的原因有很多种,比如,人们在使用手机拍摄运动对象时,成像设备就会与被拍摄对象产生相对运动,从而发生图片模糊及失真;或者有外来物体突然闯入拍摄画面,导致重新对焦时图像模糊[1]。由于某些图像时效性,不可能再重新获取,因此,采用数字图像处理使其恢复到真实、清晰的水平就显得尤为关键[2]。图像无损复原就是一种对失真图像复原方法,通过计算机进行数学计算,修复其失真像素,提高其图片质量,从而还原成清晰图像[3]。
目前,在图像复原领域,已有相关学者研究出一些相对成熟的方法。如文献[4]提出了一种基于点扩散函数(PSF,point spread function)估计的运动模糊图像复原方法,该方法分别对PSF中运动模糊方向及长度进行最优估计,由此生成PSF最优参数,并将其用于模糊图像的复原处理。虽然该方法能更进一步还原模糊图像信息,但是它在计算小尺度模糊时,波动很大,复原效果不理想。文献[5]设计了一种基于改进维纳滤波的运动模糊图像恢复算法,利用模糊角度估计方法检测模糊方向,根据极径累加值选取Hough变换或Radon变换获得模糊方向检测结果,并结合改进维纳滤波复原方法实现参数的自动设定,对边缘像素的振铃效应进行抑制,实现模糊图像复原。文献[6]提出一种基于PSF尺寸预估计的天文图像复原优化算法,该文献通过基于边界测度的PSF尺寸预估计方法对稀疏测度PSF估计算法进行优化,继而对PSF尺寸进行预估,得到精准的PSF数值,提高图像复原的精度。然而上述方法在实际拍摄曝光时间内,相机与拍摄对象间的相对位移易产生误差,导致复原结果不清晰的问题。为此,本文运用模糊图像沿模糊角偏移特性,采用Radon变换原理,应用PSF估计参数构造恢复图像模型,并采用维纳滤波方法还原模糊图像。
1 模糊图像退化模型设计
数字图像恢复的前提在于退化模型的建立,模糊图像退化模型如图1所示。

图1 模糊图像退化模型
输入原始图形函数f(a,b),其中a和b表示图像坐标的横向和纵向变量。经过退化函数h(a,b)配合噪声函数n(a,b)进行运算,得到退化图像g(a,b)。通俗来说就是原始图像f(a,b)通过一种变动h(a,b)加上噪声n(a,b)的影响变成了模糊图像g(a,b)[7]。此过程中,h(a,b)为图像变模糊的具体过程,该函数把实际遇到的问题转换成PSF模型,该模型中的参数即为模糊度参数[8]。
假定物体对象在空间中的相互位移是线性的,则输出图像g(a,b)可由式(1)得到[9-11]:
g(a,b)=h(a,b)*f(a,b)+n(a,b)
(1)
根据理性化模型将,由于存在多种线性运动导致图像模糊,因此根据理性化模型将他们分为N个线性运动,由此得到退化函数[12-14]:

(2)
式中:C表示模糊尺度,即运动模糊方向上像素移动的距离;β表示运动模糊方向,即相对运动方向和水平方向的夹角。
当沿水平正方向做匀速直线运动而导致运动模糊[15],h(a,b)表示为

(3)
通常情况下,频谱相图中条纹与模糊方向是相互垂直的,根据这一特性,测量出频谱图中相对运动方向和水平方向的夹角,来估计PSF运动模糊方向。
2 参数估计
2.1 运动模糊方向参数估计
基于上述模糊图像退化模型,对运动模糊方向估计参数进行估计,将基于空间笛卡尔坐标系的函数用极坐标(ρ,θ)表示,其在原平面下的一条直线在极坐标的表示下就都为同一点,叠加成一定厚度,根据这一特性,原平面内所有直线的存在性都可从极坐标(ρ,θ)平面上直观表示出来,将图像中的某个像素点用函数表示,求其在笛卡尔坐标系下某方向的积分转变成极坐标(ρ,θ)下点的测量。其原图像中高亮条纹转换到极坐标(ρ,θ)下就变成一个亮点,其原图像中暗亮条纹转换到极坐标(ρ,θ)下就变成一个暗点[16-18]。
在实际参数估计过程中,首先对图像进行灰度化,对其进行数学建模,然后进行傅里叶变换,得到频谱图,使其居中扩大发现其条纹呈明暗相间、等距平行排布,其条纹方向的垂直方向就是所求模糊度方向,然后在其区间[1°,180°]进行变换,从而获得一个列数为180的矩阵R,每一列数值就是该方向笛卡尔坐标系变成其在极坐标(ρ,θ)下某位置的数值,其在极坐标下投影的最大值就是明暗相间条纹的方向,也就是矩阵R中最大值,通过查找最大值在矩阵R中的所在列,由此获取模糊运动方向[19-20]。
2.2 模糊尺度参数估计
假设模糊度C为运动模糊图形的第2个参数,模糊尺度C表示拍摄设备在曝光过程中,拍摄设备与被拍摄对象间相对位移,采用径向基函数神经网络来估计模糊度尺度。此技术具有完全贴合及以全局为目标函数,计算出全局最优解,并不是基于各位置优化算法,为当前一种较高级反馈式神经网络,由于性能优良,算法能得到最真实解。用RBF作为内置空间的一个个元素,对输入值分别进行计算,使输入的低维度函数变成高维度函数,最后对每个运算结果进行加权求和得到最终结果。径向基函数在算法中的第1次变换,即从原始函数到内置空间的元素是非线性变换,而第2次从低维度函数变成高维度函数是线性变换。
在这一过程中,采用高斯基函数来求解非线性基函数,高斯基函数计算步骤较少,条理性逻辑性强,输入多个变量也不混乱,曲线光滑,存在任意次导数,且具有对称性。
利用RBF神经网络完成对模糊尺度参数的估计,把估计结果与实际拍摄曝光时间内相机与拍摄对象的相对位移比较,就可以算出模糊尺度的误差,提高参数估计精准度。
3 维纳滤波图像无损复原
估计出模糊度2个参数后,采用维纳滤波复原法进行复原,此方法采用原始图像f(a,b)与复原图像F(a,b)间的最小二乘法估计准确值,使其均方差最小,此方法能最大程度还原图像。尽管维纳滤波是目前最常见的一种复原图像的手段,但也有不足,因为其中的均方差准则会计算所有的误差,无论条件如何,都会对所有误差进行加权平均计算,然后求取平方值。为了提高计算效率,降低图像噪声的影响,也为了符合人类关注关键部位的第一感觉,优化后的维纳滤波技术图像复原原理如下:
(1)对整体进行去卷积;
(2)采用对模糊图像进行划分的方法进行逐个复原,虽然划分越多,噪声影响会与划分个数成正比,严重影响其还原质量,但是这种噪声影响会被引导在不重要的区域,使其关键部位比传统方法真实;
(3)对图像进行重叠划分,减少图像分割时带来的边界干扰问题,以1 024×1 024图像为例:原划分方法是将原图片划分为2的整数幂次,假定现在分为32块,每块大小32×32,改进的方案为外推3个像素,变成36块大小为38×38的图像,对中间区域优化复原对边界进行适当的忽略。
4 结果与分析
为验证基于模糊度参数估计的数字媒体图像无损复原方法的有效性,设计如下实验。将本文方法与文献[4]中的基于PSF估计的运动模糊图像复原方法(传统方法)进行对比,主要对比模糊方向、模糊角度的估计效果以及图像复原的结果。
4.1 模糊方向估计实验
先使用传统的估计方法进行估计,得到不同模糊尺度下不同模糊方向结果,如表1所示。
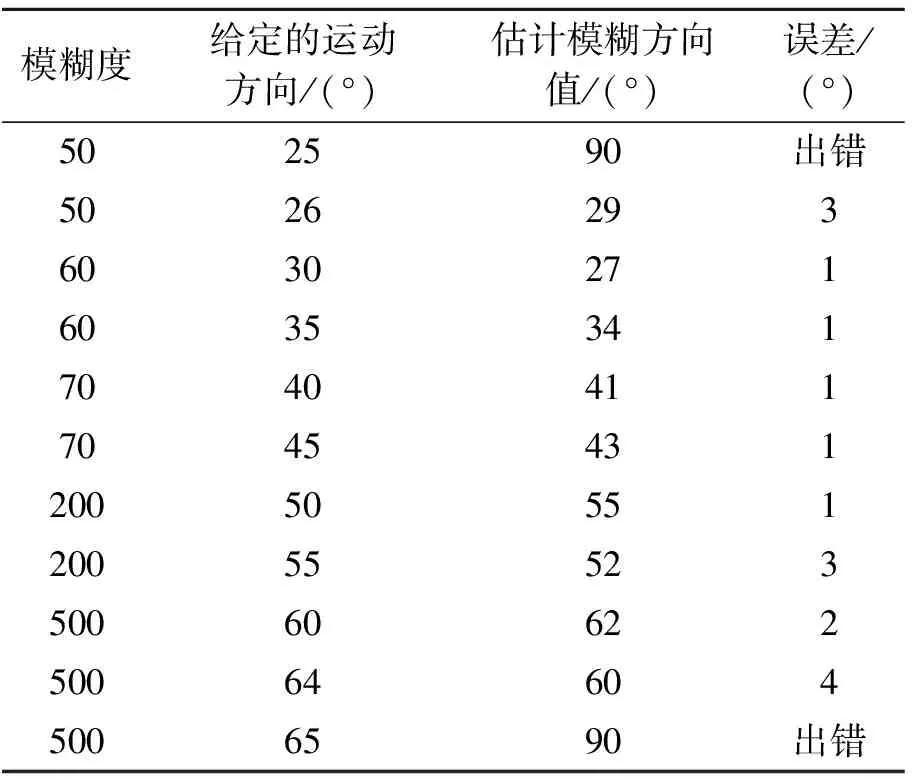
表1 传统方法模糊方向参数估计结果表
从表1可知,传统的估计模糊方向参数在30~60°范围内误差限度不超过1°,能够准确估计出模糊方向参数,但在其他小角度及大角度境况下,其估计模糊度参数值会出现很大偏差,根据实验得知,出现变差最大角度为90°或者180°。
采用模糊度参数估计方法,令90°或者是180°的结果为0,然后对新矩阵重新运算,重新查找其最大值。得到的最大值即为模糊方向,模糊度参数估计方法实验结果如表2所示。

表2 本文方法模糊方向参数估计结果
从表2可知,模糊度参数估计方法比传统方法计算速度更快,不必逐个判断图像是否受十字标记影响,将其赋于零,既简单准确又方便快捷,整体的模糊方向参数估计误差都在1°范围内。
4.2 模糊尺度估计实验
采用本文方法对模糊尺度参数进行估计,并与传统方法进行对比,实验结果如表3所示。

表3 不同方法的模糊尺度实验结果对比表
实验结果表明,传统方法仅在实际模糊长度较小时比较准确,而本文方法的模糊尺度估计结果不受实际模糊长度的影响,始终保持较高的准确性。
4.3 复原图像结果评价
根据上述对模糊方向和模糊尺度验证分析可知,采用模糊度参数方法复原结果更为精准,为了进一步验证基于模糊度参数估计的数字媒体图像无损复原方法的有效性,利用现有的主观评价和客观评价2种方法对图形的复原质量进行判定。
由于主观评价方案如人类第一感官一样,往往比较注重图形中比较重要地方,然后观察整体图像是否清晰,整体图像是否光滑等等。虽然评价结果具有第一实用性,但是难免会加入人的主观思想,而且不会定量给出评价结果,因此需要采用客观评价方法进行研究。
客观评价方法一般采用峰值信噪比、均方差等方法,客观评价方法通过对复原图像每一个像素与原图的每一个像素进行对比,来定量判断图像质量,其结果好坏不一定能够满足人类主观感觉,因此采用以下方法进行对照评价。
(1)对全局复原性进行判定 对全局复原性进行判定,图像复原模糊/粗糙度对比结果如表4所示。

表4 2种方法图像复原模糊/粗糙度对比表
从表4可知,传统方法对原始粗糙度小的复原率比较高,并且模糊度参数估计方法复原率明显优于传统复原方法。
(2)直观印象判定 采用直观印象进行判定,2种方法对比结果如图2所示。
从图2可以直观的看出,模糊度参数估计方法比传统方法在关键部位——脸部,具有明显优势,复原结果十分清晰,传统方式显得比较模糊而且有锐利感,不平滑;从整体上看模糊度参数估计方法也比传统方法看上去较为清晰,模糊度参数估计方法边缘较中心稍微模糊,整体过度平滑,比较符合人类观察事物的第一印象,而传统方法图像中心与边缘有的地方清晰度不一致,有些边缘甚至比关键部位清晰,所以模糊度参数估计方法比传统方法优势较为明显。
5 结 论
(1)在获得PSF中的模糊方向及模糊尺度两个参数的基础上,通过参数转换来估计模糊度方向参数,能够有效降低误差;
(2)由于模糊度参数估计方法通过RBF神经网络结构计算输入函数,直接将估计结果和相机与拍摄对象相对位移比较,不必逐个判断图像是否受十字标记影响,使得复原过程简单准确又方便快捷;
(3)采用优化后的维纳滤波技术对图像进行复原,采用原始图像与复原图像间的最小二乘法估计准确值使其均方差最小化,能够最大程度还原图像,使图片整体平滑,复原效果更好。

