基于LBM与Matlab GUI的流体力学可视化教学与虚拟实验

刘向东, 戴含晖, 陈永平,,3

(1.扬州大学 电气与能源动力工程学院，江苏 扬州 225127；2.东南大学 能源与环境学院，南京 210096；3.苏州科技大学 环境科学与工程学院，江苏 苏州 215009)

0 引 言

流体力学是力学的一个重要分支，主要研究流体内的力学规律，是水利工程、化学工程、动力工程等诸多学科的理论基础，在航空航天、船舶制造、能源电力等领域有着广泛应用[1-2]。流体力学有着理论性强、抽象难懂的特点。特别是，在多数高校的流体力学教学中，各类理论性极强的概念、案例往往只能通过陈述/推导公式的方式传授给学生，学生在学习过程中难以获得直观体验，这大大削弱了他们的接受度和学习兴趣，进而明显影响到了教学效果[3-5]。

随着计算机技术和计算流体力学理论的发展，对流体力学教学及实验案例进行数值虚拟仿真能够直观清晰地展现流体力学相关规律，从而为改观传统教学方法形式单一、教学成效有限的现状提供了一种有效手段[6-8]。传统计算流体力学方法通过数值化求解以非线性偏微分纳维尔-斯托克斯方程组(Navier-Stokes equations)为核心的宏观连续性流体力学控制方程来实现对流体力学问题的虚拟仿真，其数值化编程和计算求解过程都相当复杂，并且求解计算量大、计算效率一般，从而限制了其在流体力学教学与实验领域的普及。为解决这一问题，本文将使用有别于传统计算流体力学方法的格子玻尔兹曼方法(Lattice Boltzmann method，LBM)[9-10]来进行典型流体力学问题的数值模拟仿真。与传统计算流体力学模拟方法不同，LBM基于分子动理论，通过对微观粒子行为的统计平均来反应流体宏观动力学特征，是一种典型的介观模拟方法。相较于传统计算流体力学方法，LBM具备先天的并行特性，且物理背景清晰、边界条件处理简单、程序易于实现、计算效率高[11]，已经在许多传统计算流体力学模拟方法难以胜任的领域都获得了成功应用[12-13]，近年来逐渐受到了国内外研究者的关注。

值得注意的是，Matlab软件中的图形用户界面(Graphic User Interface，GUI)工具可通过添加控件设计人机交互界面，便于搭建可视化仿真实验平台，已应用于数学、物理、力学等课程教学中[14-16]。鉴于LBM方法在流体力学高效模拟计算和Matlab GUI工具在用户操控与可视化方面所具有的优势，结合LBM方法和Matlab GUI工具设计搭建流体力学虚拟实验仿真平台，用于高校流体力学教学实验中，为进一步丰富流体力学课堂与实验教学手段、提高课堂与实验的教学效果提供一种崭新工具。

1 LBM简介

LBM基于分子动理论，将流体抽象为大量只有质量没有体积的微观粒子，这些粒子可以向空间的若干方向任意移动。LBM将粒子的演化过程分为碰撞和迁移两个阶段，因此格子玻尔兹曼方程可以分解为两个部分。

(1)

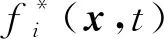
在数值模拟过程中根据流场空间维数的不同，有不同的离散速度集和与之对应的平衡态分布函数。针对二维的计算区域，选择D2Q9模型(2维空间，9个离散速度，见图1)，其流场被一系列正方形划分。其速度、局部平衡分布函数、权函数及声速分别如下：

(2)

图1 D2Q9模型示意图

在获得速度分布函数后，流体的宏观密度与速度通过以下公式计算得到：

(5)

计算过程中固体界面处的边界节点使用非平衡外推的方法，该节点上分布函数计算方法如下

(6)

式中,x+为壁面法向的相邻节点的位置。

LBM的演化过程可分解为碰撞和迁移两个过程，其计算流程图如图2所示，具体的计算步骤如下：

步骤1给定初始密度ρ和速度场u；

步骤2计算平衡态分布函数feq；

步骤3在时刻t执行碰撞过程，发生改变的节点x上的粒子分布函数为原有粒子分布和碰撞项之和；

步骤4执行迁移，节点x上的粒子以速度ei运动到与节点x相邻的x+ei，粒子分布函数也随之迁移；

步骤5边界处理；

步骤6计算时刻t+1的密度ρ与速度u；

步骤7重复步骤3～6直到满足终止条件。

图2 LBM方法计算流程图

2 功能模块

2.1 整体设计思路

采用Matlab GUI工具对LBM模拟计算方法进行封装，便可建立起流体力学虚拟实验仿真平台，其用户界面如图3所示。由图可知，本文所建立的仿真平台主要包含顶盖驱动流、泊肃叶流和卡门涡街模块。3个模块对应着流体力学中的几个经典问题。该仿真平台的逻辑结构如图4所示。

图3 流体力学虚拟实验仿真平台用户界面

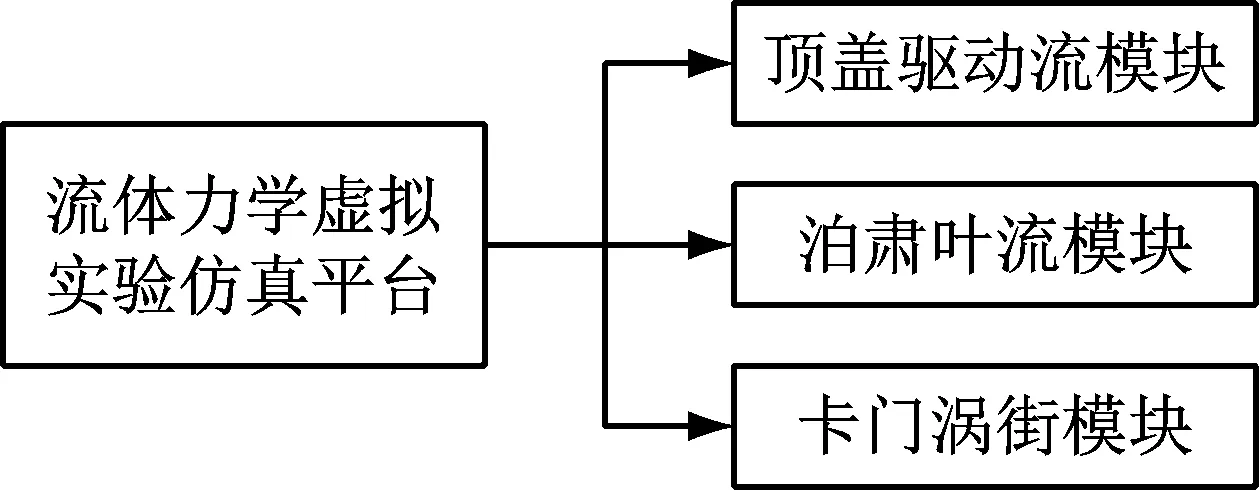
图4 流体力学虚拟实验仿真平台模块结构图

2.2 顶盖驱动流模块

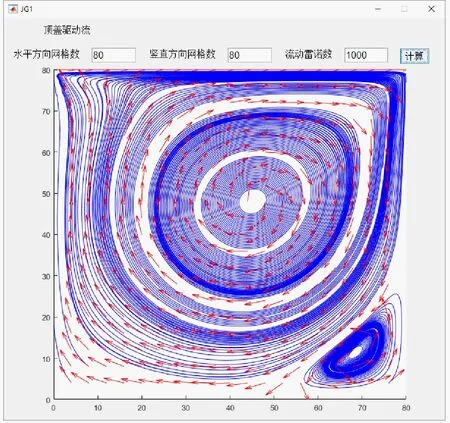
顶盖驱动流是通过腔体顶盖水平滑移运动驱动腔体内流体产生流动的典型流体力学问题。不同工况条件下的顶盖驱动流流场内蕴含着复杂流体力学现象(诸如不稳定层流、多级涡及湍流等)，从而使之成为流体力学教学中的经典物理模型之一。为此，本文建立的流体力学虚拟实验仿真平台特包含了顶盖驱动流模块，其用户界面如图5(a)所示。该模块为用户提供了自定义计算区域尺寸与流动雷诺数的功能。用户可通过文本框分别键入计算区域水平方向网格数、竖直方向网格数、流动雷诺数，然后点击“计算”按钮完成模拟操作。顶盖驱动流的不同流动状态主要受流动雷诺数影响。在输入计算区域几何尺寸后，在显示计算结果的区域内会给出网格划分示意图(图5(b))。图6显示了不同雷诺数条件下，同一个方腔内的流体流动的LBM模拟计算结果。

由图6可见，整个流场中的流线由蓝色线条表示，计算区域中的速度矢量场用红色箭头表示。值得一提的是，为了让图中表示速度的矢量箭头显示得更加清晰，在绘制过程中对整个速度场做了标准化处理，即所有速度矢量的模都设为相同。这样，图中红色箭头便可直观展示流场内各处的速度方向信息。从图中可以发现，随着雷诺数Re的增大，在中央1级涡的右下部、左下部和左上部会依次逐渐出现2级涡。Re=200时，方腔右下部的2级涡已有形成的趋势，到Re=1 000时右下部的2级涡已完全成型。当Re提升到4 000时方腔左下部会出现2级涡。当Re=700时，方腔左上部的2级涡也已初步形成。基于该模块中流线与流体速度矢量的可视化展示，学生可以在图中清晰的获得方腔内流体流动的详细流场分布，并能够直观地感受到流动状态在很大程度上与流体流动的雷诺数直接相关。

2.3 泊肃叶流模块

深入了解泊肃叶流的流动规律是研究更为复杂流动问题的基础。本文建立的流体力学虚拟实验仿真平台也纳入了泊肃叶流模块，其用户界面如图7所示，计算区域的网格尺寸与入口流速可通过对应的文本框键入，再点击“计算”按钮便可获得模拟结果。图中显示的是计算区域内水平速度的分布云图。从图右侧的颜色图例可以看出，颜色由浅入深表示的是速度由大到小的变化过程。水平方向的速度分布总体呈现从流道中央向两侧递减的规律。图中还显示了中央某界面上的速度分布图，用红色箭头与轮廓线标出，这使得计算结果更加直观清晰。值得注意的是，在计算区域左侧流体流入部分存在一定的过渡段。这是由于在给定入口流速时是平均分布的，由速度平均分布演变为充分发展段内抛物线状的速度分布需要一定的过渡段。同时，考虑到不同入口流速下泊肃叶流速度云图分布相似，该模块还设置了计算模拟数据导出功能，为用户获得不同工况下通道内充分发展段主流速度分布的具体计算模拟结果提供了有效接口。利用该功能，图8给出了不同入口流速条件下充分发展段的水平方向速度分布的模拟结果。如图所示，学生可以观察到两平板间的流动大致呈现二次方函数的抛物线分布，垂直于流体流动方向的流动速度由流道中央向通道两侧壁面递减，直至壁面上速度降为0。该模块可以为学生直观形象地认识流体力学中典型的泊肃叶流主流速度分布特征提供一种有效手段。

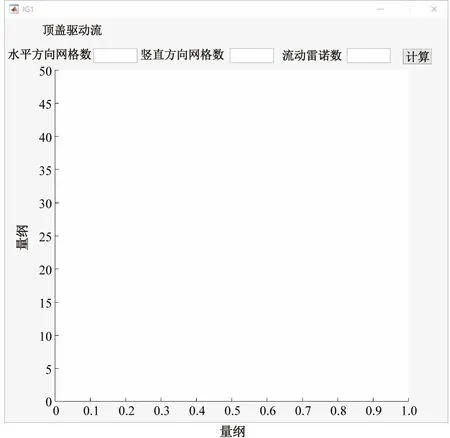
(a) 用户界面图

(b) 计算网格图

图5 顶盖驱动流模块用户界面及计算网格图

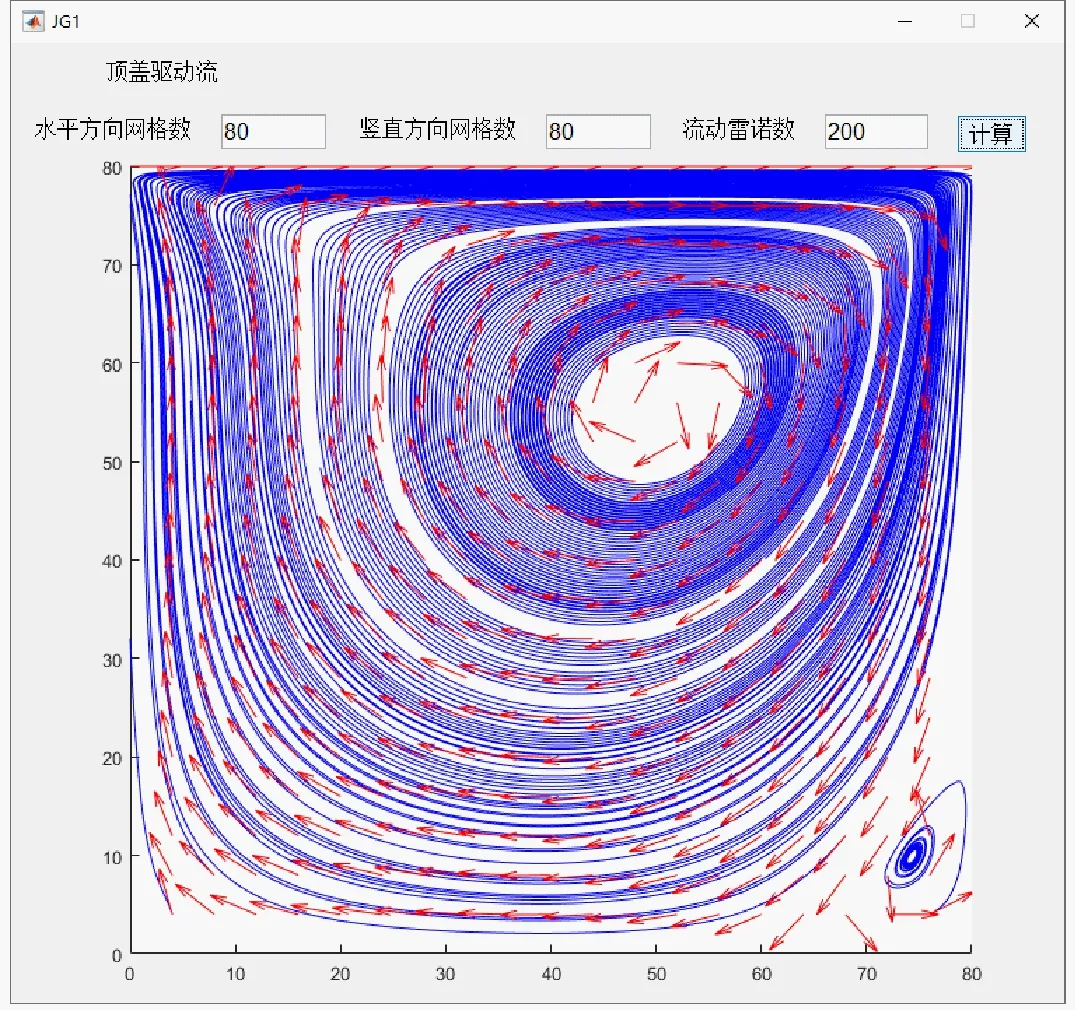
(a) Re=200

(b)Re=1 000

(c)Re=4 000

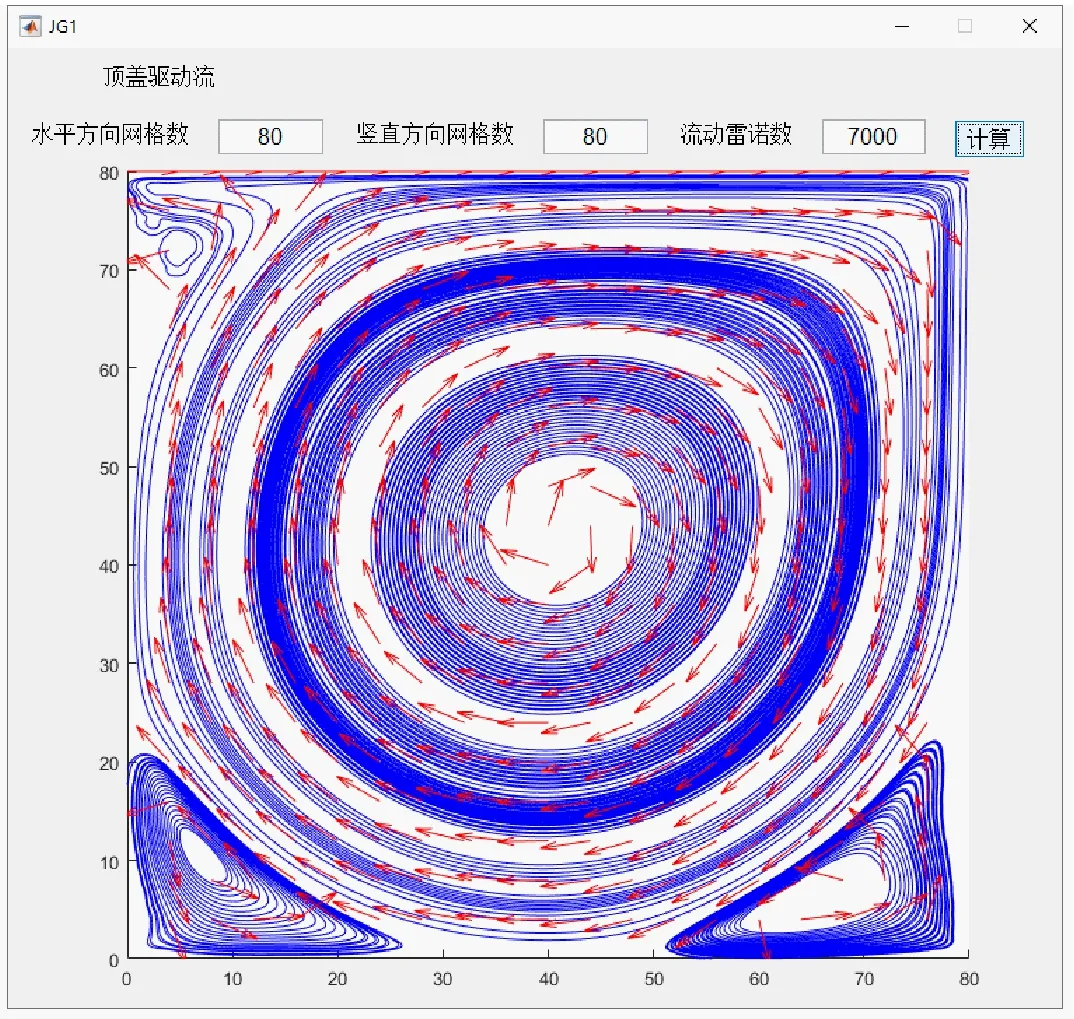
(d)Re=7 000

图6 不同雷诺数条件下顶盖驱动流的计算结果

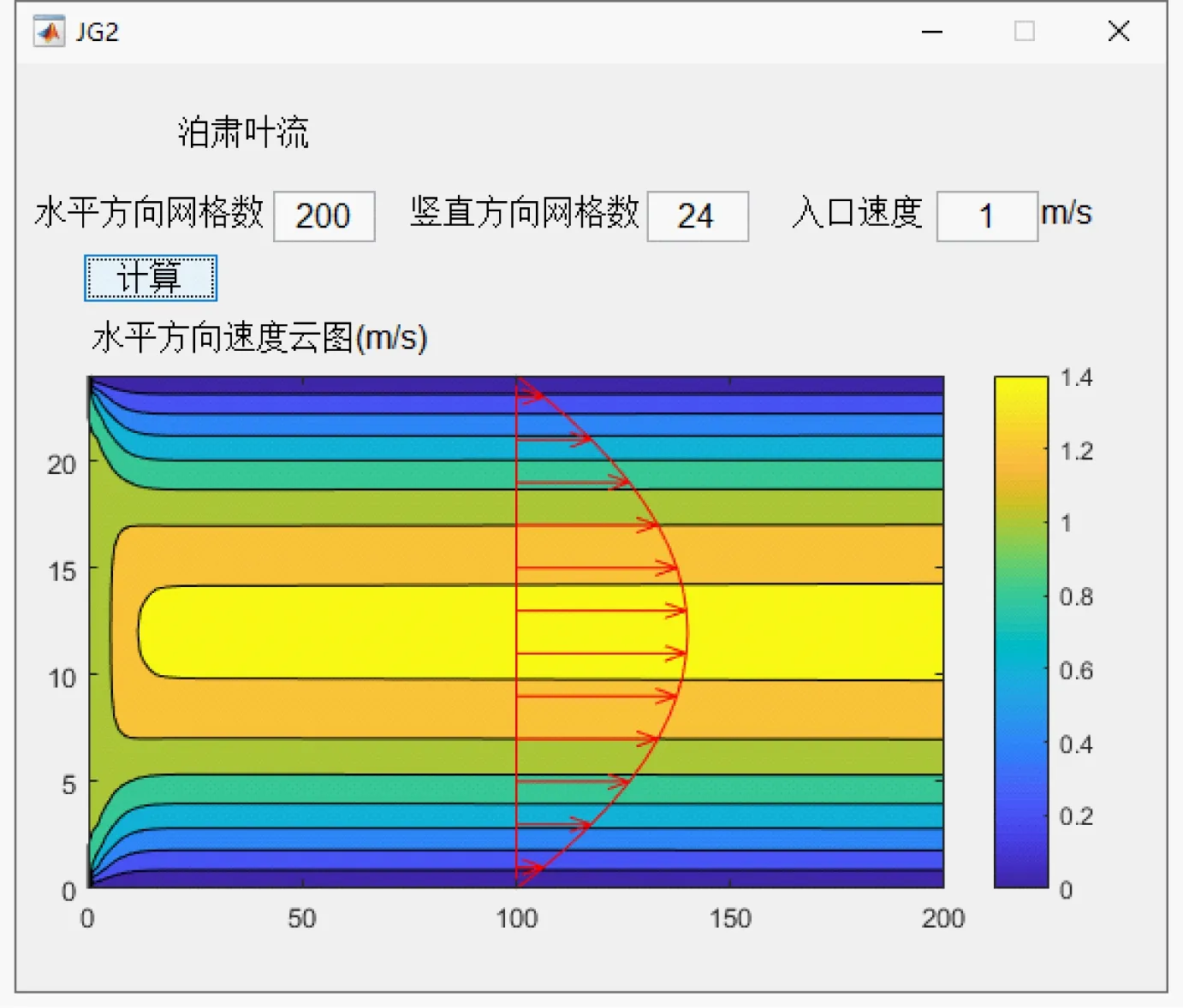
图7 泊肃叶流模块用户界面

图8 不同入口流速条件下泊肃叶流主流速度分布

2.4 卡门涡街模块

卡门涡街是当定常来流绕过流场中的障碍物时，障碍物两侧周期性脱落形成旋转方向相反、排列规则的双列线涡的流体力学现象。在不同的来流速度与障碍物尺寸条件下，障碍物之后的卡门涡街特征各异。本文流体力学虚拟实验仿真平台所包含的卡门涡街模块用户界面如图9所示，演示的是二维圆柱绕流问题。该模块允许用户调整入口流速u、障碍物直径与流道宽度比pr，可以实现对卡门涡街特征的模拟与直观展示。从模拟计算结果可见，该模块可以直观地展示出不同工况下计算区域内流体速度大小连续分布的流场云图，计算结果界面还给出了每个模拟计算工况所对应的不同尺寸圆柱障碍物的轮廓示意。图9(a)～(c)显示的是圆柱直径一定、入口流速不同的条件下，各个流场计算结果的对比。图9(a)中的入口流速为30 m/s，该条件下整个计算区域内的流动较为平稳，在圆柱的后方基本没有出现线涡脱落的现象。当入口流速增大到250 m/s(见图9(b))，圆柱之后出现了明显的扰动，但随着流动向下游发展，这一扰动也逐渐趋于缓和。而继续增加入口流速到500 m/s(见图9(c))，可以发现在圆柱之后的整个计算区域内都出现了明显的线涡脱落现象。当在图9(c)的基础上将障碍物半径占流道宽度的比例从0.3减小到0.1时(见图9(d))，圆柱后的流场波动仍然显著，但波动幅度相较于图9(c)有所减小而波动频率则有所增加，这就说明随着障碍物半径占流道宽度比例的减小，卡门涡街所产生的线涡强度有所减小，同时其脱落频率则有所提升。通过以上算例，学生可以直观地认识到，在流体绕障碍物流动的过程中，流体流速较高时更易在障碍物后产生卡门涡街，并且涡街产生的频率和强度与障碍物与流道间的尺寸比例直接相关。

3 虚拟仿真实验平台在教学活动中的应用方式与优势所在

本文建立的流体力学虚拟实验仿真平台为学生提供了一个直观、清晰认知经典流体力学的有效窗口，为改观传统陈述/推导公式型的教学方法提供了契机。任课教师在课堂教学过程中可以通过引导学生在计算机上进行仿真平台的实际操作来加深对经典流体力学的理解认知，并直观体会到关键工况参数对流体流动特性的影响。同时，教师还可以就此向学生引申介绍后续《计算流体力学》《数值传热学》等相关课程的基本思想，进一步拓展学生的知识面，并为其未来专业课的学习打下良好基础。

相对于传统流体力学教学方法，使用Matlab GUI设计的流体力学仿真模拟实验平台进行辅助教学的优势明显：

(1) 具有良好的可视化效果。虚拟实验仿真平台最显著的优点就是具备良好的可视化效果。通过矢量场图、流线、速度云图将各个算例清晰直观地展现在学生面前，有利于强化学生对该方面知识的理解，为后续内容的学习打好基础。

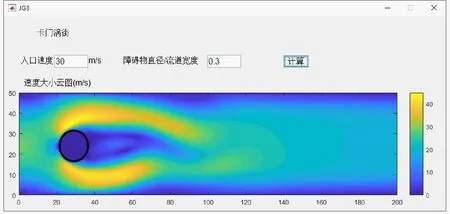
(a) u=30 m/s，pr=0.3

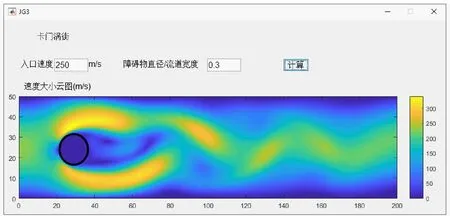
(b) u=250 m/s，pr=0.3

(c) u=500 m/s，pr=0.3

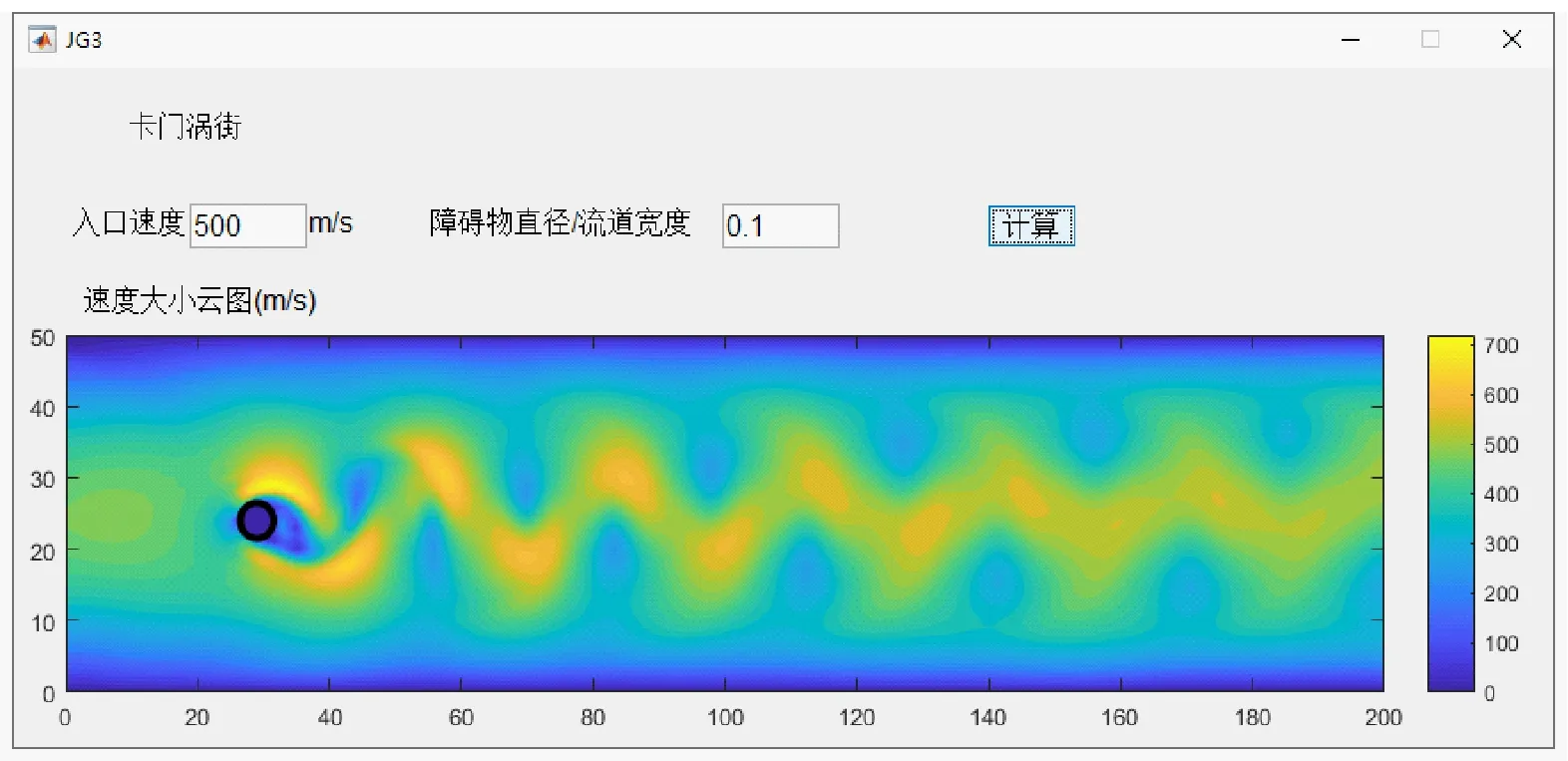
(d) u=500 m/s，pr=0.1

(2) 操作简单，运行速度快。本文所建立的虚拟仿真实验平台界面清晰，操作简便。同时，该平台基于LBM方法进行数值模拟仿真，且本文已根据Matlab GUI的运行特点对程序内的运算逻辑做了优化。因此，相较于基于传统计算流体力学方法的数值仿真平台，该平台运行速度得到了明显提升，可在几分钟内获得合理计算结果。

(3) 其他优势。该平台所基于的LBM方法，边界条件处理简单，程序易于实现且开源，学有余力的学生可以通过自行编译程序，对几个流体力学问题进行自主模拟。这充分体现了“因材施教”的教育理念，并有助于进一步提升学生的计算机程序编译水平。虚拟仿真实验平台节约了实验过程中的耗材耗能，成本低廉、节能环保，从而实现了“绿色教学”。

4 结 语

采用LBM对流体力学教学中的经典案例进行了数值模拟，并基于Matlab GUI工具对其进行封装，开发了流体力学虚拟实验仿真平台。该仿真平台主要涵盖了流体力学知识体系中顶盖驱动流、泊肃叶流和卡门涡街3个经典案例模块。学生可以在平台用户界面上输入可变工况参数进行计算，并可以获得流场中的速度矢量场、流线等重要信息的直观展示。同时，学有余力的学生还可以通过自行编译程序，对几个流体力学问题进行自主模拟。

相对于流体力学传统课堂与实验教学方法，本虚拟仿真实验平台具有可视化效果好，计算速度快，界面清晰操作简单，教学成本低廉，方便交流等优点，有助于激发学生的学习兴趣，加深学生对抽象概念与复杂流动状态的理解认识，课堂与实验教学效果的提高，值得在流体力学教学中进行推广。