应用差分进化算法进行波阻抗反演

(四川水利职业技术学院，四川 崇州，611231)

引 言

波阻抗反演是油气勘探中储层预测的有效方法之一，同时也是一个非线性优化问题。在求解非线性问题上，传统的优化手段存在着一些不足，导致对有些函数容易陷入局部解而难以得到全局最优解，收敛速度也较慢。而非线性优化方法在求解这类问题中有较强的全局优化能力，因而在地球物理反演中已得到了高度的重视。近几年相继出现了各种各样的进化优化算法均被引入到波阻抗反演中[1，2]。从目前研究的结果已表明，非线性优化方法的反演结果大多优于线性反演方法，它们的共同特点就是能实现解的全局最优[1]。

差分进化算法(Differential Evolution，DE)是新近提出的一种智能优化方法，已被证明在求优过程中具有高效性、收敛性、鲁棒性等优点[3，4]。差分进化算法可以采用实数分量合成参数矢量，因此描述问题的方式接近实际；同时其采用的变异操作具有微调功能，加之进化过程控制变量较少；算法通用，不依赖于问题信息；算法原理简单，容易实现。根据这些优点，本文应用差分进化算法进行波阻抗反演，并应用理论模型和实际数据进行验证。对于理论模型，反演的结果与原始模型非常吻合；从实际数据处理效果来看，算法能较好地反演出结果，其中存在着相邻道反演出来的波阻抗整体趋势是一致的，只是具体数据存在一些差异，需要做平滑处理。试验表明：应用差分进化算法进行波阻抗反演方法是可行的，有效的。

1 差分进化算法

差分进化算法[5]是一种基于实数编码的具有保优思想的全局优化进化算法。它是由Storn等人于1995年提出的，最初的设想是用于解决切比雪夫多项式问题，后来发现DE也是解决优化问题的有效技术。其适于求解一些利用常规的数学规划方法所无法求解的复杂环境中的优化问题。

1.1 基本差分进化算法

为求非线性函数f(x1，x2，…，xD)的最小值，进化过程中的第G代利用NP个D维参数向量构成种群{xi，G，i=1，2，…，NP}，种群大小NP在进化过程中保持不变。

1.1.1 种群初始化

在D维空间，随机产生满足边界约束的NP个向量构成初始种群：

xji，0=randj·(bj，U-bj，L)+bj，L

(1)

其中，randj为区间(0，1)上的随机数，bj，U和bj，L分别为第j个变量xj的上界和下界。

1.1.2 变异

对每一个目标向量xi，G，在{1，2，…，NP}范围内随机选择3个互异整数r1，r2，r3，且使得i≠rj(j=1，2，3)，得到变异向量：

vi，G+1=xr1，G+F·(xr2，G-xr3，G)

(2)

其中，变异因子F∈(0，2)为一常数，控制偏差向量的放大程度。

1.1.3 交叉

为增加种群的多样性，按如下方式得到试验向量：

(3)

式中：rnbri∈{1，2，…，D}为随机选择的序列，用它来确保ui，G+1从vi，G+1至少获取一个分量。交叉因子CR∈[0，1]。

1.1.4 选择

差分进化的选择方案基于局部竞争机制，如果ui，G+1的目标函数值小于xi，G的目标函数值，则令xi，G+1等于ui，G+1；反之，令xi，G+1等于xi，G。

在有边界约束的问题中，必须确保产生新个体的参数值落在问题的可行域中，一个简单方法是将不符合边界约束的新个体用在可行域中随机产生的参数向量代替。

1.2 差分进化算法其他形式

上面介绍的是最基本的DE操作程序，实际应用中还发展了DE的多个变形形式，并用符号DE/x/y加以区分，其中x限定当前被变异的向量是“随机的”或“最佳的”；y是所利用的差向量的个数。利用这个表示方法，前面叙述的基本DE策略可描述为DE/rand/1。其他多种形式，主要体现在变异操作的不同，如：

(1)DE/best/1

vi，G+1=xbest，G+F·(xr1，G-xr2，G)

(2)DE/best/2

vi，G+1=xbest，G+F·(xr1，G-xr2，G+xr3，G-xr4，G)

(3)DE/rand/2

vi，G+1=xr1，G+F·(xr2，G-xr3，G+xr4，G-xr5，G)

(4)DE/rand-to-best/1

vi，G+1=xi，G+F·(xr1，G-xr2，G)+λ·(xbest，G-xi，G)

实际反演计算标明，DE/rand-to-best/1算法既保持了种群的多样性，又具有较快的收敛速度，为此本文选取该计算模式计算波阻抗反演。

2 波阻抗反演数学模型

地震道反演的褶积模型可以表示为：

Y(t)=b(t)×R(t)

(4)

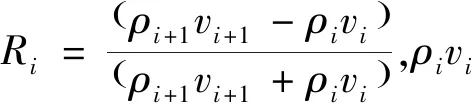
由褶积模型可以知道地震记录与反射系数为非线性关系，因此，求取反射系数或波阻抗的过程为非线性的。地震道非线性最优化反演就是求取下列目标函数的极值问题：

目标函数：f(Z)=∑[X(i)-Y(i)]2

(5)

式中，Z即ρv为波阻抗序列；X为原始地震记录；Y为模型响应，由反演出的反射系数(或由波阻抗计算得到的)与地震子波的褶积计算得到。找到目标函数f，于是很容易知道差分进化算法的搜索空间为Z或R的空间。本文是在R空间进行反演。具体实现：差分进化算法的每一维就对应地下某一地层的波阻抗Zi。地下介质分为n层，则算法个体的维数就是n。差分进化算法的任意一个体就是在波阻抗空间里进行搜索，每搜索到一个新位置就相当于构建了一个新的波阻抗模型。对每个新的波阻抗模型，可以用式(4)求取模型响应，然后带入目标函数式(5)就可以算出各个个体的目标函数值。比较新个体的目标函数值与旧个体的目标函数值优劣，选择优者作为新种群中的个体。这样通过反复的进行迭代最终得到了最优解，即能最佳反映原始地震道的波阻抗模型。

3 算例分析

为了验证算法的可行性和有效性，本文分别给出了下面两部分内容，第一部分给出了反演方法在理论模型试算，从反演结果分析算法的有效性和可行性。第二部分给出了应用算法对实际数据的处理。

对于差分进化算法中的控制参数，本文通过查阅相关文献[1，5，6]和试验，最终是这样选取的：种群规模NP取500，缩放比例因子K取[0.4，1]之间的均匀分布随机数，交叉概率CR取0.9，加权因子λ取0.8。算法的退出条件为：①目标函数达到要求；②迭代次数达到一定的次数。

3.1 理论模型试算

波阻抗理论模型如图1所示，图2为合成地震记录。所采用的Ricker子波，主频为30Hz，采样点为30个，采样间隔为2ms。

图1 波阻抗理论模型

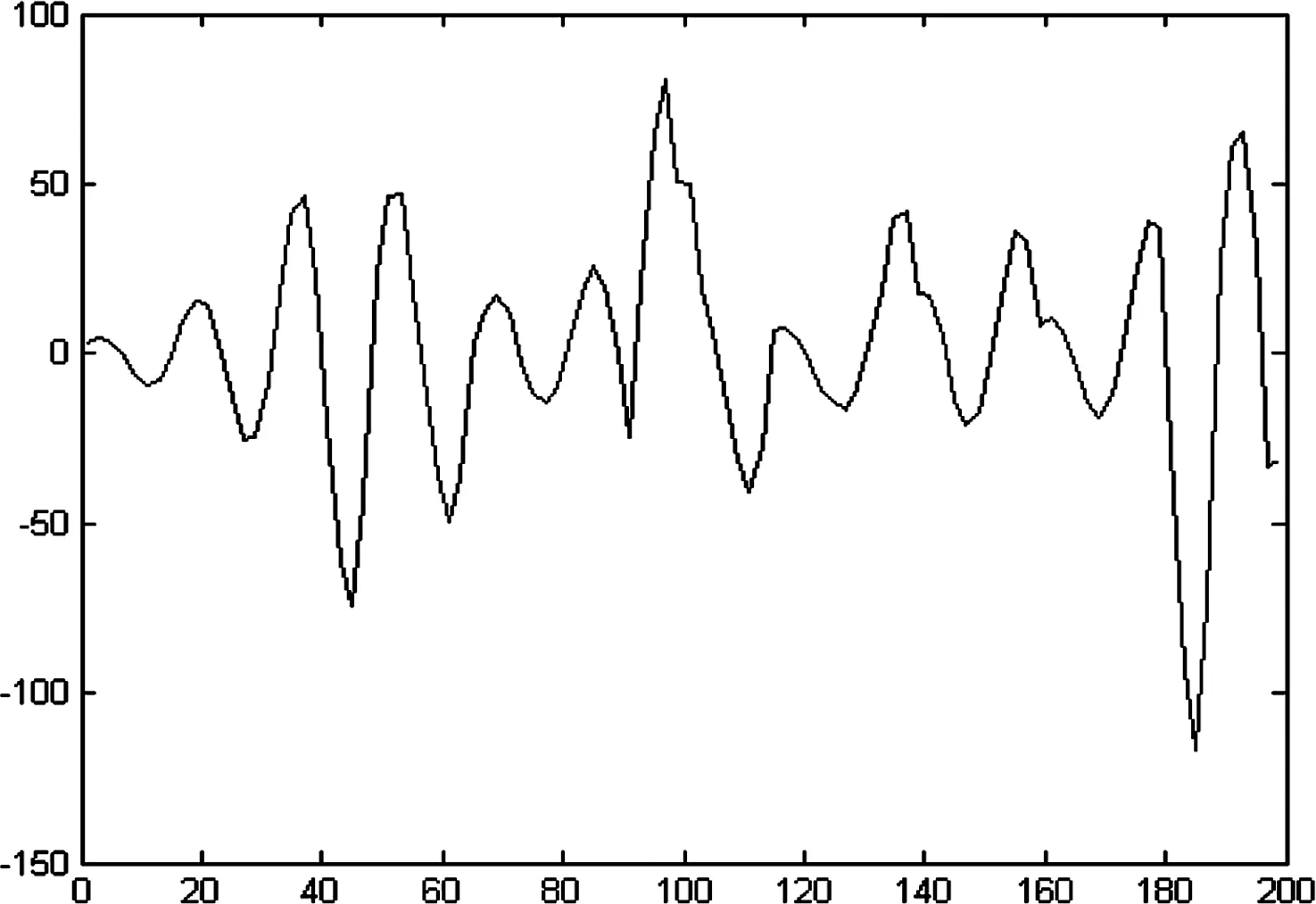
图2 正演得到的地震道

根据模型进行反演得到的结果如图3、图4所示，其中图3为反演得到的波阻抗模型与原始模型的比较图，图4为反演后的地震记录与合成地震记录的比较图。

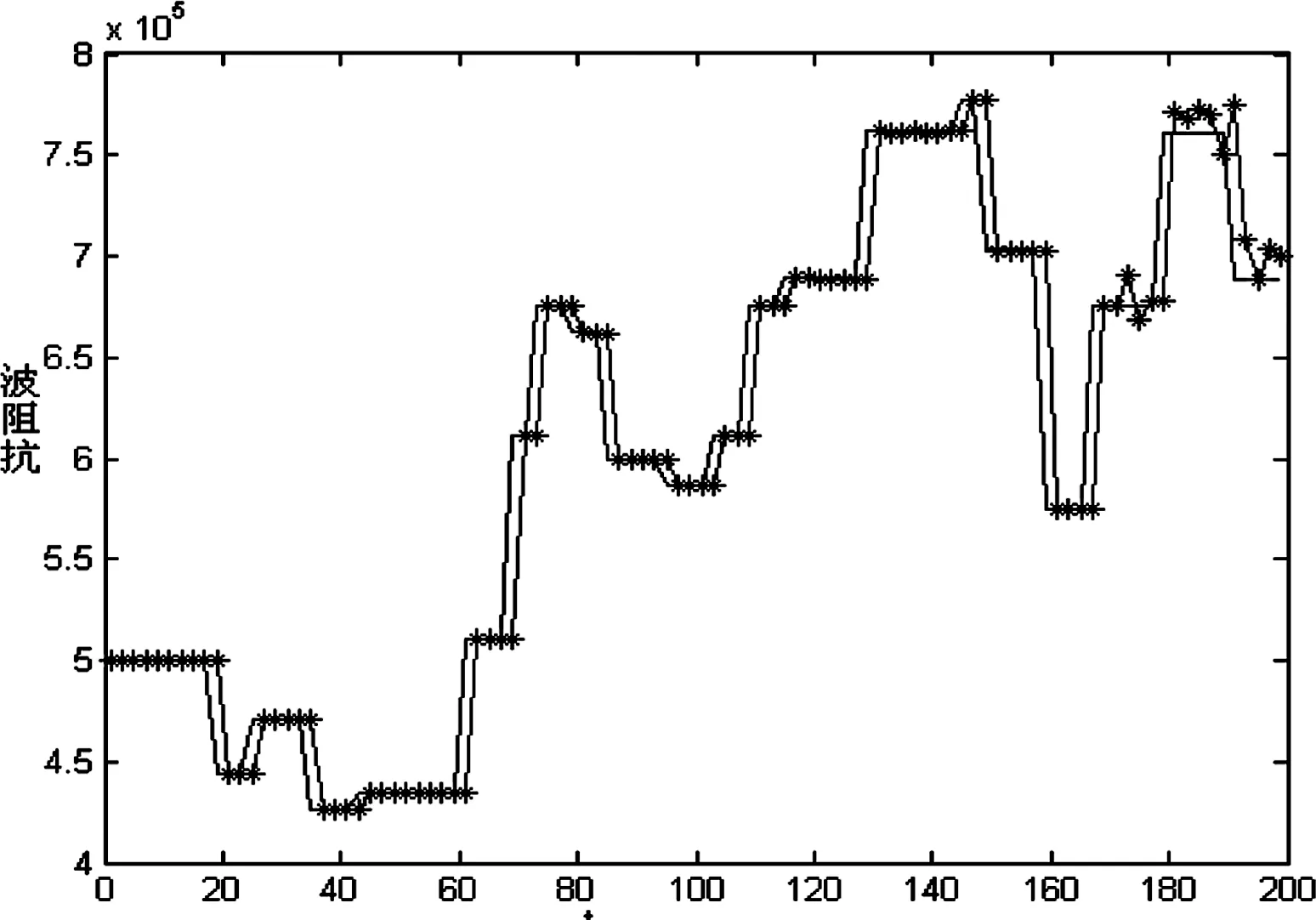
图3 反演波阻抗模型与原始模型比较

(其中--为原始波阻抗模型，-*-为反演波阻抗模型)

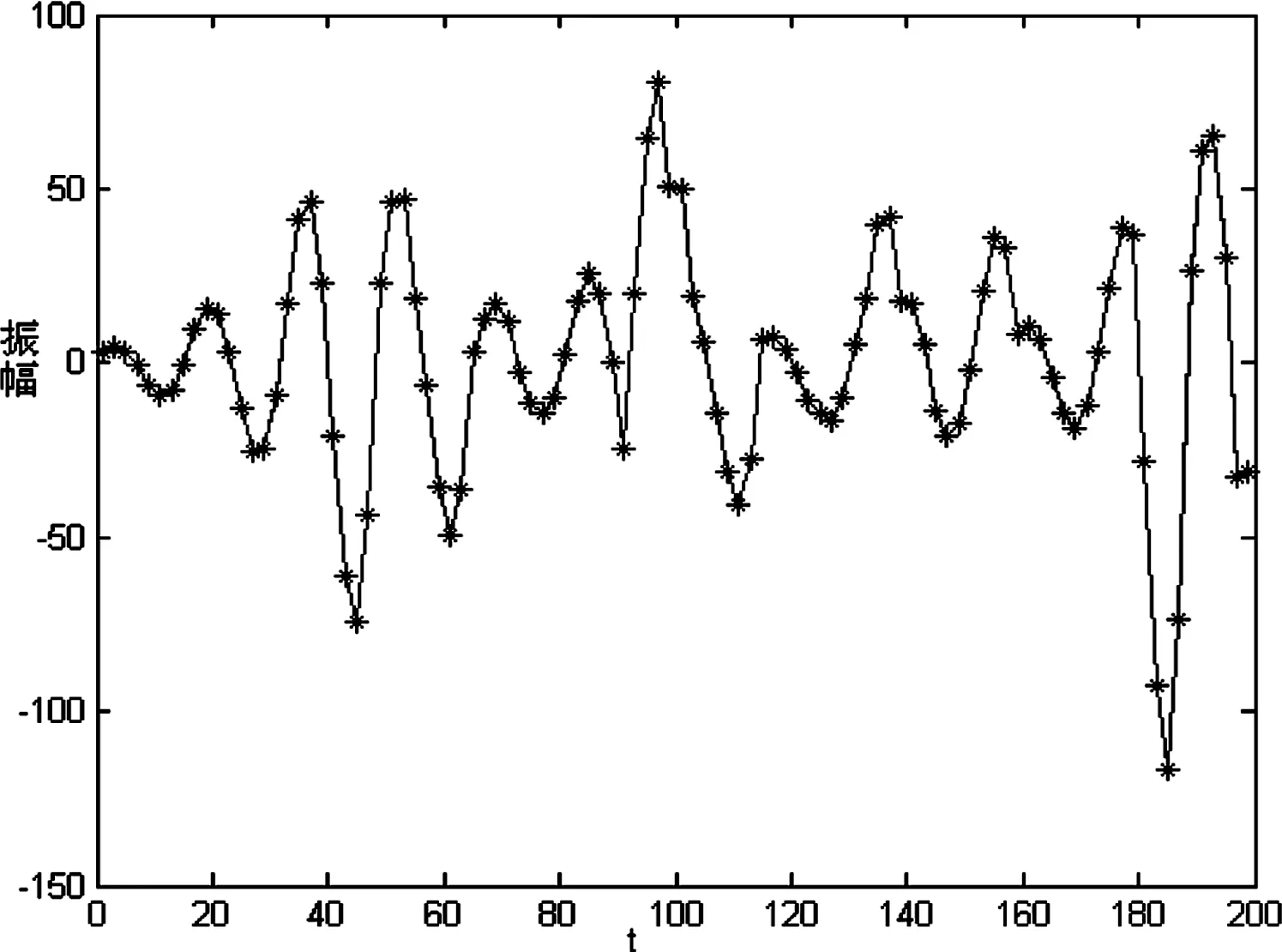
图4 反演后地震记录与合成地震记录比较

(其中--为原始地震记录，-*-为反演地震记录)

从反演得到的结果来看，算法能较好地解决波阻抗反演问题，由此可见，应用差分进化算法进行波阻抗反演是可行的。

3.2 实际资料反演

为了验证算法处理实际资料的效果，笔者选取某一地震剖面中的一段，如图5所示，从中提出的子波如图6所示。子波有32个采样点，采样间隔为2ms。

图5 地震剖面

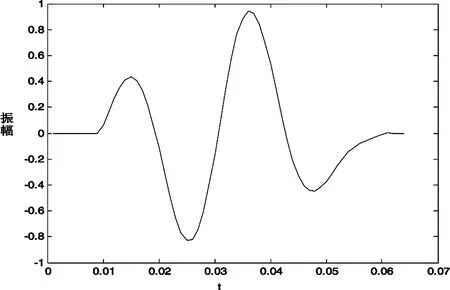
图6 地震子波

对其中一单道反演的结果如图7-图10所示。

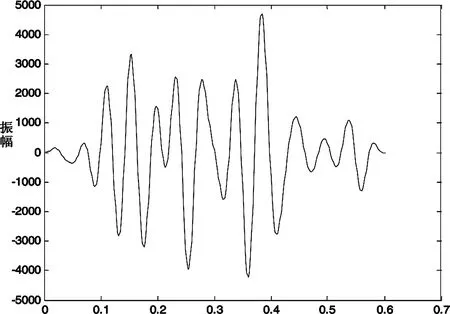
图7 第18道地震记录

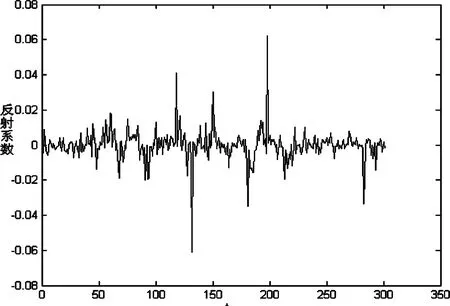
图8 反演得到的反射系数

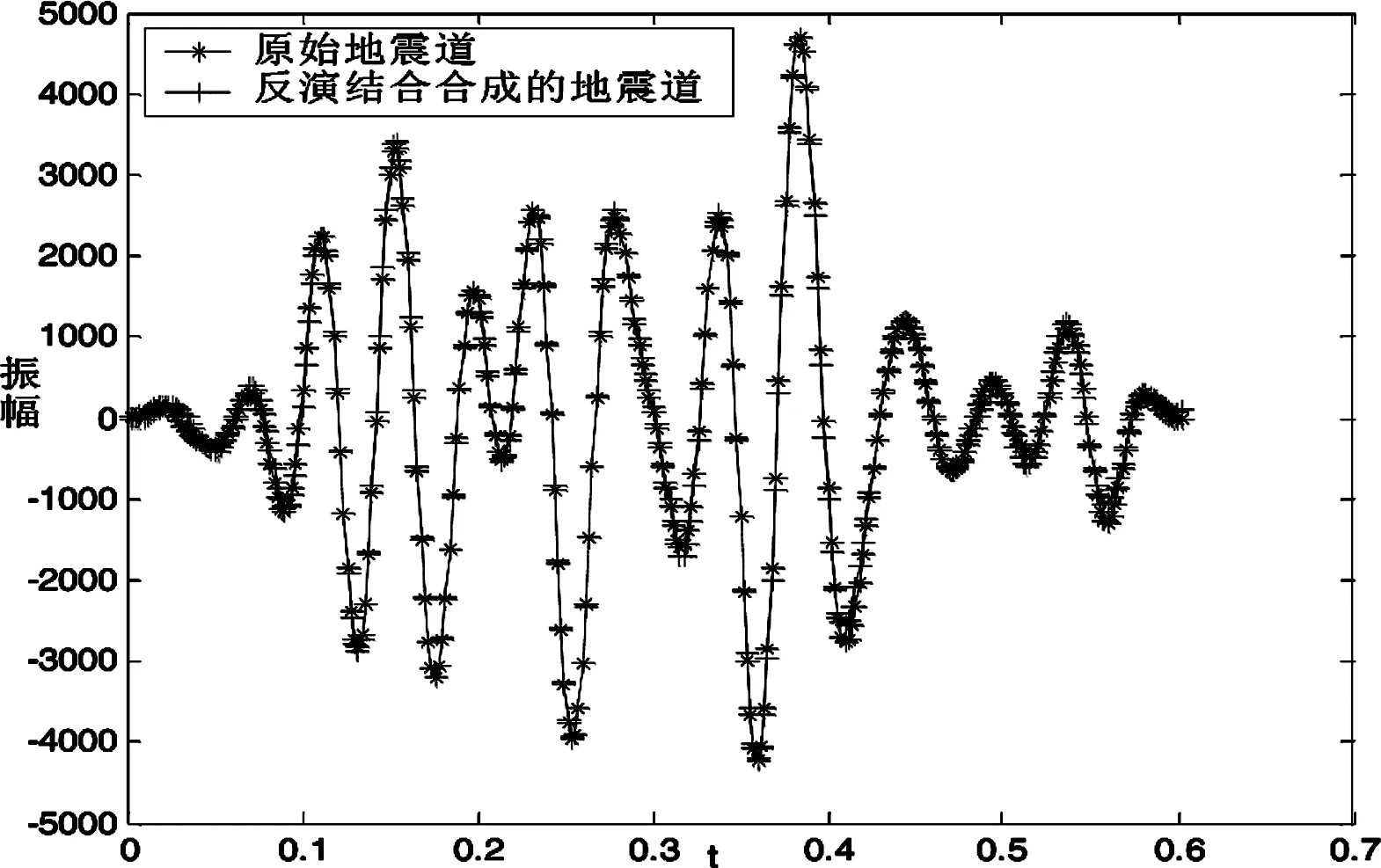
图9 对应的地震道比较

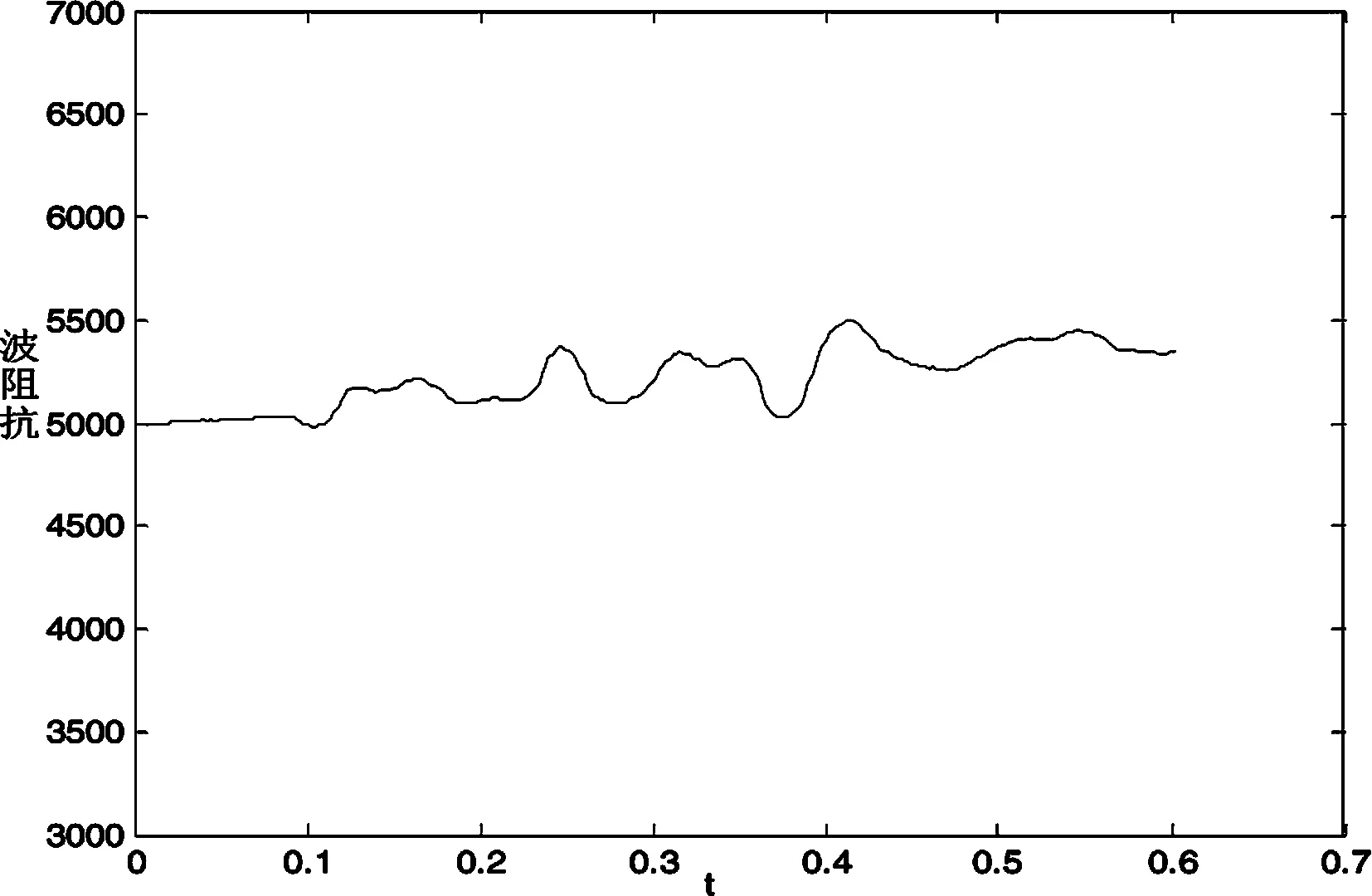
图10 相应的波阻抗

整个剖面逐道反演并对反演得到的波阻抗做平滑处理可得到的结果：如图11、图12所示。

图11 反演得到的地震剖面

图12 对应的波阻抗剖面

在处理实际数据中，算法对地震道拟合的很好，达到0.981，而且反演出来的波阻抗整体趋势是一致的，只是相邻道之间具体数据存在一些差异，需要用平滑处理。可见算法反演的结果是可行的，有效的。

4 结论

通过研究差分进化算法，提出地震波阻抗反演的差分进化算法的实现方法，并应用C++编程实现，将该方法应用于实例进行试算。从理论模型试验的结果可以看出，差分进化算法进行波阻抗反演是收敛的、稳定的；从实际资料处理效果来看，算法能较好地反演出结果，其中存在着相邻道反演出来的波阻抗整体趋势是一致的，只是具体数据存在一些差异，需要用平滑处理。应用差分进化算法进行波阻抗反演的方法是可行的、有效的。