基于跨尺度精细方法的面板坝面板损伤演化尺寸效应分析

邹德高，陈楷，余翔，于逸姝，张仁饴

(1.大连理工大学 水利工程学院；海岸和近海工程国家重点实验室，辽宁 大连 116024；2.郑州大学 水利科学与工程学院，郑州 450001;3.广州市城市规划勘测设计研究院，广州 510060)

猴子岩、大石峡、拉哇等工程的规划建设，标志着中国面板坝规模正突破200～300 m级跨越[1]。面板是保证此类高坝大库安全的关键防线，探讨其地震下的损伤破坏规律，并定位薄弱部位，具有重要意义。

近年来，研究人员开展了诸如挤压边墙损伤分析[2]、双层面板抗裂措施研究[3]、地震破坏机理研究[4-5]、填筑蓄水期面板脱空分析[6]、考虑界面接触效应的影响研究[7]等工作，取得了丰硕的成果。但目前对面板损伤演化规律讨论较少[8-9]，未见网格尺寸对面板应力及损伤规律的影响效应研究。

本文采用Quadtree跨尺度方法，高效建立12个精细分析模型，联合土体广义塑性模型和混凝土塑性损伤模型，并通过SBFEM-FEM耦合分析方法，开展250 m级面板坝静动力数值分析，研究网格精细化对面板损伤演化规律的影响，建议面板损伤分析中宜取的网格尺寸，给出面板易损区范围及其特点。

1 跨尺度精细建模与分析方法

1.1 Quadtree离散技术

Quadtree[27]根据设定的精度条件，通过对几何域进行递归四分来获得跨尺度的精细分析模型。用于面板坝分析的优势有：正方形单元比例大，单元精度最高且具有几何相似性；跨尺度实现了精细化分析精度与计算代价间的良好平衡；单元具有水平分层特性，自动满足坝体填筑模拟要求(见图1)。

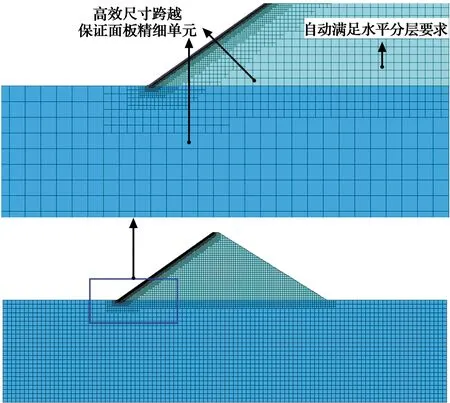
图1 Quadtree离散的面板坝跨尺度网格Fig.1 Cross-scale mesh of concrete face rock-fill

1.2 面板坝跨尺度精细模型

图2 面板法向离散单元分层Fig.2 Layering of discrete face elements along

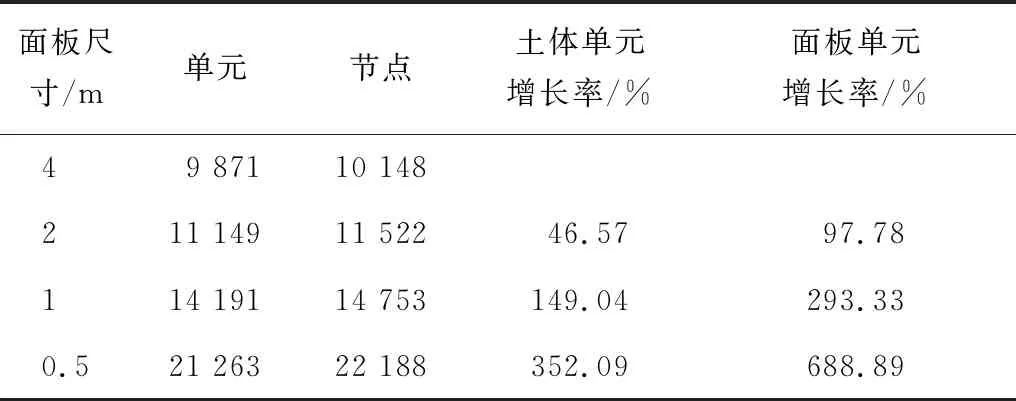
表1 面板坝跨尺度分析模型信息Table 1 Model information for cross-scale analysis of concrete face dam

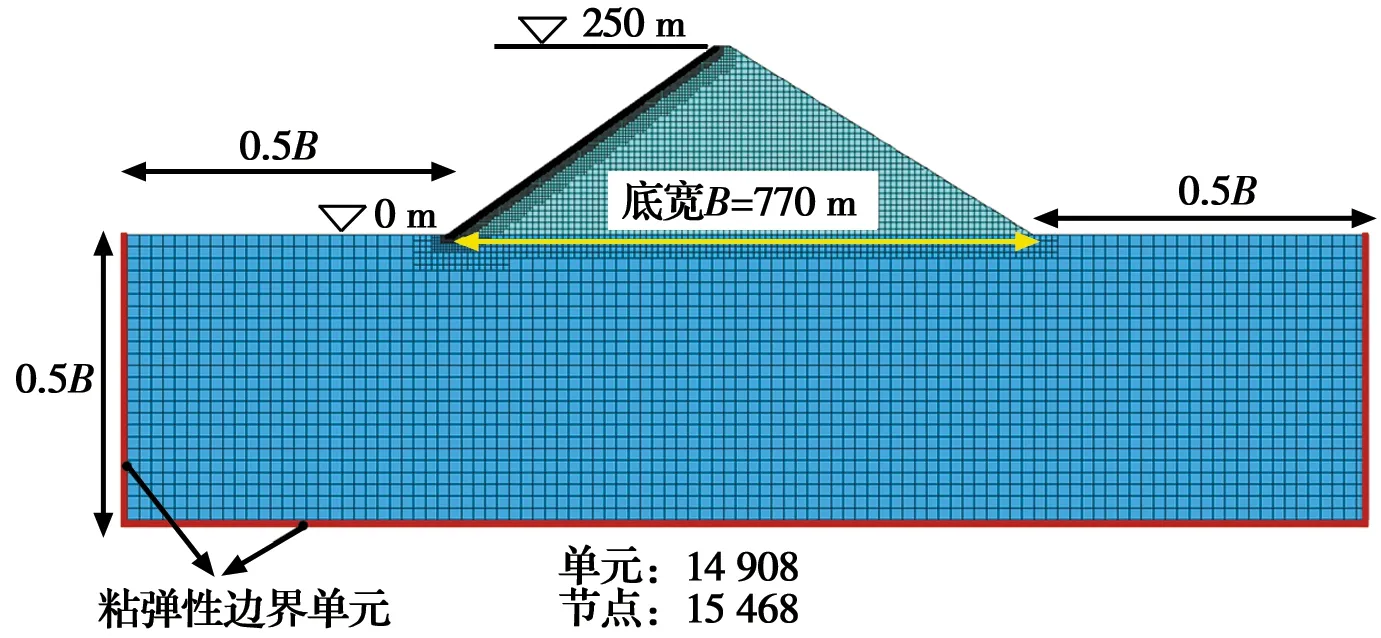
图3 面板坝四分树网格(面板顺坡向尺寸1 m)Fig.3 Quadtree grid of concrete face dam (face size is 1 m)

通过四分树跨尺度方案建立精细网格，使得整体单元量增加很少，尤其土体单元增长不多，跨尺度有效减少了精细分析的计算量，可有效提高分析效率。

1.3 耦合的SBFEM-FEM分析方法

如图4所示，在坝体和坝基网格中，包含常规三角形、四边形单元，也包括传统方法难直接求解的多边形单元。通过传统等参FEM计算常规单元，采用作者发展的非线性SBFEM可直接求解生成的多边形单元，在程序内部仅需给定不同的单元类型号，即可实现无缝耦合分析。

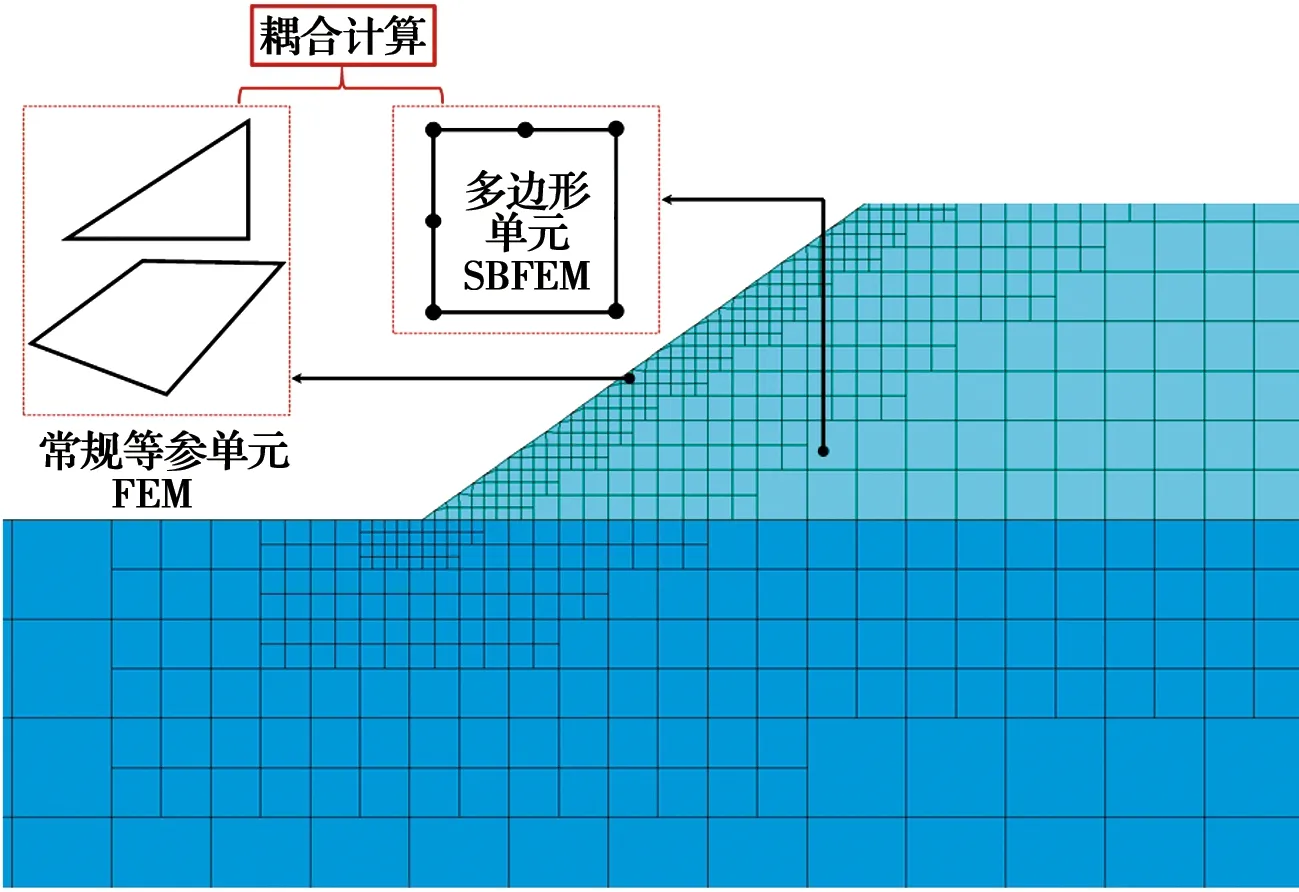
图4 耦合计算中单元类型分配示意Fig.4 Schematic diagram of element type assignment

这里简要介绍多边形SBFEM单元理论，通过边界离散、径向解析思路，可直接获得任意多边形插值函数Φ和应变位移矩阵B，参见式(1)和式(2)。

(1)

(2)

通过域内积分点，可求出多边形单元刚度矩阵。

(3)

代入相关变量，可解得内外力向量，见式(4)～式(8)。

(4)

(5)

(6)

(7)

(8)

通过迭代求解力学平衡方程，见式(9)，可获得计算域的数值解，详细理论推导及实现过程参见文献[10]。

(9)

大连理工大学工程抗震研究所基于Visual C++平台，通过类抽象、继承等面向对象设计方法、并行计算等先进的开发技术，自主开发了Windows版本的大型岩土工程非线性分析程序GEODYNA[28]，并已推广应用于50多个大型水电、核电、水运工程和地下结构等工程项目。

基于该平台，集成了多边形SBFEM单元，丰富了传统分析方法的灵活性和通用性，可以实现SBFEM-FEM的耦合分析，并兼容了所有常用的土石坝筑坝材料本构模型。

2 面板坝损伤分析

2.1 计算参数

采用堆石料广义塑性模型[29]、混凝土塑性损伤模型[30]、弹塑性接触面模型[6]开展面板坝静动力数值分析，参数列于表2～表5。其中，土体广义塑性模型中：G0、K0分别为弹性体积模量和剪切模量；Mg为临界状态线在p′-q平面的斜率；Mf、αf、αg为模型参数；H0、Hu0为塑性模量参数，趾板及基岩采用线弹性模型；β0、β1、γDM为模型参数，详细理论推导介绍参见文献[31]。弹性模型参数Dn0、Ds0，临界状态参数e、λ、Mc，塑性流动方向α、γd、km，加载方向参数Mf，塑性模量参数H0、k、fh，颗粒破碎参数a、b、c，详细理论介绍可参见文献[32]。损伤模型中：ft为最大抗拉强度；fc为最大抗压强度；Gt为混凝土材料断裂能。线弹性参数见表6，缝单元法向压缩刚度为25 GPa/m，法向拉伸刚度为5 MPa/m，切向刚度为1 MPa/m。静力计算考虑了坝体的填筑和蓄水过程同步进行，坝体填筑分34个荷载步完成，其中，面板分3期浇筑，计算步为13、25和34，水位蓄至240 m高程。

表2 筑坝材料广义塑性模型参数Table 2 Generalized plastic model parameters of dam material

表3 过渡料广义塑性模型参数Table 3 Generalized plastic model parameters of transitional material

表4 混凝土塑性损伤模型参数Table 4 Plastic damage model parameters of concrete

表5 广义塑性接触面参数Table 5 Parameters of the generalized plastic interface model

表6 线弹性材料参数Table 6 Parameters of linear model

动力计算中，采用规范谱人工波，顺河向峰值加速度取0.3g，竖向峰值加速度为顺河向的2/3，加速度时程见图5，持续时长为40.00 s，计算时间步间隔取为Δt=0.005 s。

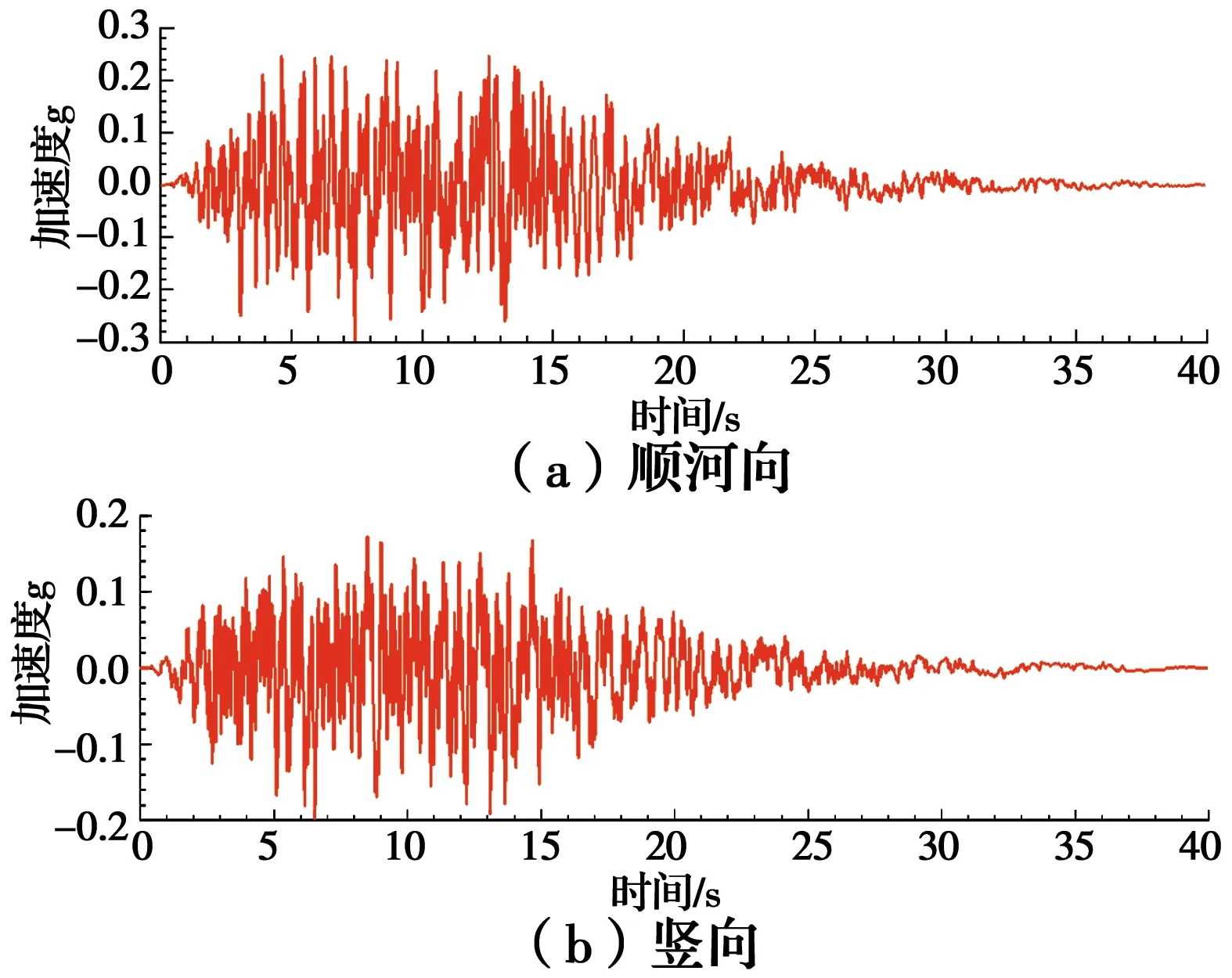
图5 地震波加速度时程曲线Fig.5 Time history curve of seismic wave

2.2 计算结果及分析

混凝土材料抗拉强度较低，受拉破坏较为严重，故本文主要研究面板分层及网格尺寸对其地震中拉损伤分布的影响，首先研究顺坡向尺寸的影响。

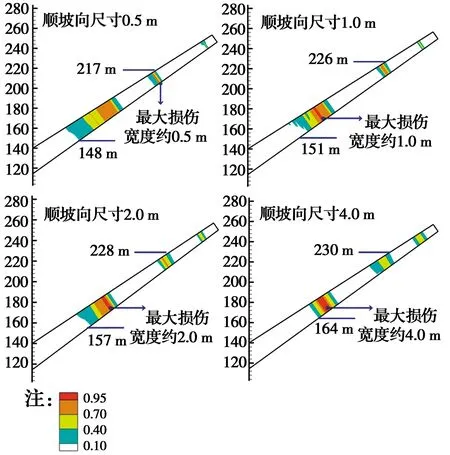
图6 面板法向离散3层网格时损伤分布Fig.6 Damage distribution of concrete face discreted three-layer mesh in normal

图6绘出了面板法向分3层网格，顺坡向取不同尺寸时的损伤分布对比。可以看出：面板破坏区域主要集中在高程150～220 m区间附近，随着网格细化，分布范围波动在10 m左右，且网格越小，损伤分布越趋局部化，有利于准确定位薄弱部位，建议面板顺坡向尺寸宜取0.5 m～1.0 m。

图7给出了面板法向分5层和3层网格，顺坡向单元尺寸取0.5 m和1.0 m时，面板整体损伤分布对比情况，可以看出：法向分3层网格时，损伤分布范围和数值与5层网格结果吻合较好，故面板法向分3层网格时，可满足计算精度。

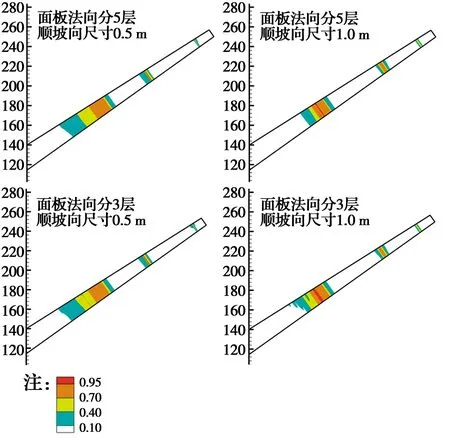
图7 面板法向离散5层和3层单元对损伤分布Fig.7 Damage distribution of concrete face discreted five-layer and three-layer mesh in normal

随后分析了面板法向分不同层网格所得结果的对比情况，如图8和图9所示，可以看出：损伤整体分布范围较为相近，故实际分析中，面板大部分区域法向可分2层(或1层)网格。但在面板顶部局部位置(见图9)，当法向分2层单元时，损伤最大位置偏上7 m左右；当分1层单元时，损伤较小，易高估面板的安全性。故该区域可考虑分3层网格，以准确定位面板薄弱位置，便于编定经济的抗震措施。

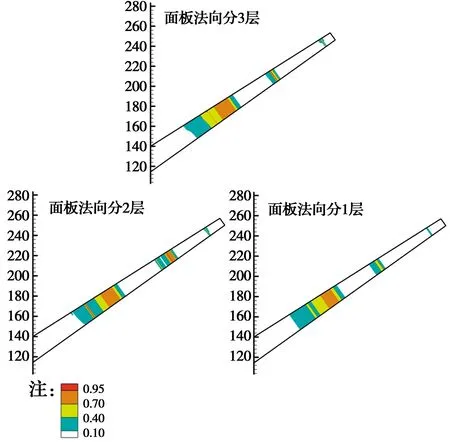
图8 面板法向离散层数的损伤分布对比(顺坡向尺寸0.5 m)Fig.8 Comparison of damage distribution of concrete face discreted different layer mesh in normal drection(dimension is 0.5 m along slope)

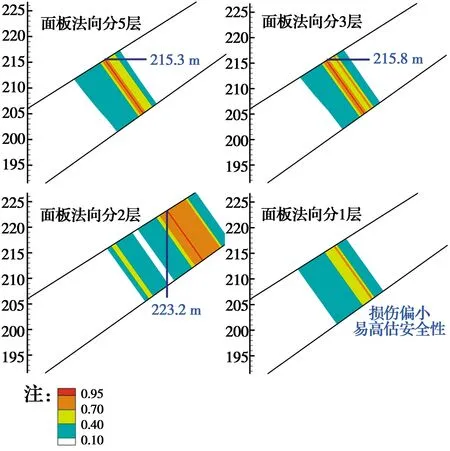
图9 面板顶部损伤分布对比(顺坡向尺寸0.5 m)Fig.9 Comparison of damage distribution on the Top of concrete face slab(dimension is 0.5 m along slope)

3 结论

采用跨尺度精细化建模和分析方法对高面板堆石坝进行了面板地震损伤演化研究，结果表明：

1)Quadtree方法可快速建立跨尺度精细分析模型。SBFEM可处理传统方法难直接求解的多边形单元(多于四边)，FEM则计算常规的三角形和四边形，通过耦合的SBFEM-FEM计算方法，实现了高效的精细损伤演化分析。

2)面板损伤区域主要发生在高程0.6H～0.9H区间附近；随顺坡向网格细化，损伤越趋局部化，越能更合理地反映面板顶部的损伤破坏现象，建议顺坡向面板尺寸宜取0.5～1.0 m；面板大部分区域法向划分2层或1层网格可达到工程精度，但对顶部局部区域，可考虑分3层网格。

3)基于Quadtree-SBFEM-FEM的跨尺度分析方法，实现了面板的精细化损伤演化规律研究，可为工程地震薄弱区域的精准定位和抗震安全控制方法的有效性分析提供重要参考和指导，且该方法具有良好的通用性，易于拓展至三维或其他复杂结构精细化分析。

4)旨在讨论跨尺度方法在面板精细损伤尺寸效应中的应用，未考虑钢筋和抗震措施的影响，这部分工作将在三维分析中开展。