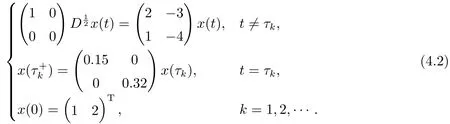具有Caputo导数的分数阶退化脉冲微分系统的有限时间稳定性 .
吴桐,张志信,蒋威
(安徽大学数学科学学院,安徽 合肥230601)
1.引言
分数阶微积分理论是关于任意阶微分和积分的理论,是整数阶微积分的一种推广,分数阶导数的记忆性,使得其能够更充分地应用于物质的记忆和遗传性质,也能够更好地模拟自然界的物理现象.特别是在最近的四十年里,分数阶微积分在现代控制理论、粘弹性理论、流体力学、凝聚态物理等各个领域得到了广泛应用,但由于分数阶微分算子所特有的奇异性和非局部性质,导致分数阶微分方程的理论研究面临一定难度.因此,对分数阶微分方程的研究具有重要的理论意义和应用价值[1−3].
自1953年苏联学者Kamenkov[4]提出有限时间稳定的概念以来,微分系统的有限时间稳定性一直是微分系统稳定性的一个重要课题,并取得了丰富的理论成果.目前国内外学者对于分数阶有限时间稳定性问题已经展开研究工作,Lazarevi´c[5−7]运用广义Gronwall不等式给出了一类分数阶线性时滞微分系统的有限时间稳定的充分性条件,此外ZHANG[8]也对该类系统给出了相关的有限时间稳定性分析.文[9-11]讨论了一类分数阶神经网络的有限时间稳定性,利用压缩映射原理、迭代以及Gronwall不等式等方法对分数阶神经网络的有限时间稳定性问题做出了详细的分析.文[12-14]中,相关学者研究并分别给出了分数阶非线性系统、分数阶时滞系统与分数阶线性时变系统在带脉冲情况下的有限时间稳定性条件.MA等在文[15]中讨论了分数阶时不变微分系统在带扰动下的有限时间稳定性问题,同时给出了相关的状态反馈,研究了系统有限时间镇定问题.最近,Phat等[16]在结合广义Gronwall不等式与Mittag-Leffler函数后给出了一类具时变时滞及非线性扰动的分数阶微分系统有限时间稳定的新的判据,该判据形式简洁且便于检验及应用.LI和WANG[17−18]通过引入滞后Mittag-Leffler型矩阵函数并利用常数变易法给出了一类分数阶齐次与非齐次时滞微分方程解的显式表达式,验证了方程解的存在唯一性,并给出了方程有限时间稳定的充分性条件.
对于分数阶线性退化微分系统的有限时间稳定性,ZHANG等[19−20]已经展开了初步的研究工作,通过代数方法得出了退化分数阶线性系统显示解的表达式,讨论了系统初值问题解的存在唯一性,并给出了该系统在带时滞情况下的指数估计与系统有限时间稳定的充分性条件.在前面学者的研究成果的启发下,我们研究同时带有扰动和脉冲现象的退化分数阶微分系统的有限时间稳定性问题.
记号:Rn表示n维欧氏空间.Rn×n为所有n×n实矩阵的集合.自然数集记为N.时间区间J=[0,T],其中T >0是有限数.对任意正定矩阵A ∈Rn×n,λmax(A),λmin(A)分别表示矩阵A的最大与最小特征根,而cond(A)=λmax(A)/λmin(A)称为矩阵A的条件数.n阶单位矩阵记为In.
2.准备知识
在这一节中,本文将给出分数阶微积分的一些定义与基本性质以及论文相关的几个定义与引理.不失一般性,本论文中所有分数阶微分、积分的下限均设为0.
定义2.1[3]设可积函数f(t)∈C[0,+∞),α>0,则记

为函数f(t)的α阶分数阶积分.
定义2.2[3]设n−1≤α 为f(t)的α阶Caputo分数阶导数. 为方便起见,以下将分数阶积分符号0Iαt与Caputo导数符号分别记作Iα与Dα. 定义2.3[3]设α>0,β >0且z ∈C,记具单参数的Mittag-Leffler函数为 而具双参数的Mittag-Leffler函数常记为 易见,β=1时,Eα(z)=Eα,1(z).而E1,1(z)=ez. 下面介绍本文中用到的引理和相关结论. 引理2.1[21]设α ∈(0,1),x(t)∈Rn为一连续可微向量函数,则有以下不等式 其中P ∈Rn×n为一常值对称半正定矩阵. 引理2.2[3]由分数阶积分及Caputo导数的定义,有 特别地,当α ∈(0,1)时,Iα(Dαx(t))=x(t)−x(0). 引理2.3[22]假定α>0,x(t)与a(t)在[0,T),(T ≤+∞)非负且局部可积,g(t)在[0,T)上连续非负且单调增加,g(t)≤M(M为常数),满足以下不等式 则 特别地,若a(t)在[0,T)单调增加,则有 考虑如下分数阶退化脉冲线性系统; 其中t ∈J.x ∈Rn为状态变量.ω ∈Rn为干扰项.A,Bk ∈Rn×n,且Bk≠In.E ∈Rn×n为退化矩阵.Dαx(t)为x(t)的α阶Caputo导数,其中α ∈(0,1). 为了研究系统(2.1),现作如下假设[23−24]: (H2)状态变量x在每个τk处左连续,即 (H3)矩阵对(E,A)是正则的,即存在复数s,使得det(sE−A)0; (H4)常值干扰项ω满足约束条件:ωTω ≤d,d ≥0. 定义2.4[25]给定两正实数c1,c2满足c1≤c2,正定矩阵R,则系统(2.1)关于(c1,c2,J,R,d)是有限时间稳定的,如果 定理3.1假定(H1)-(H4)成立,c1,c2为给定正实数,c1≤c2且存在常数γ >0,以及对称正定矩阵P ∈Rn×n,正定矩阵Q ∈Rn×n满足以下不等式,则系统(2.1)关于(c1,c2,T,R,d)是有限时间稳定的. 证考虑Lyapunov泛函 对V(x(t))关于t沿系统(2.1)的解求α阶Caputo导数,由引理2.1及条件(3.1a)有 而由定理条件,Q正定,从而ωTQω ≤λmax(Q)ωTω ≤λmax(Q)d,则(3.3)化为 由引理2.2,对(3.4)两边同时进行α阶分数阶积分,得 由条件(3.1c),∀k ∈{1,2,··· ,m},都有 从而,(3.5)式变为 结合(3.6)及引理2.3,有 这样,结合(3.7),(3.8),(3.9)及条件(3.1b),有 消去λmin(P1),即得xT(t)ETREx(t) 定理3.2假定(H1)-(H3)成立,ω=0,c1,c2为给定正实数,c1≤c2且存在常数γ >0,以及对称正定矩阵P ∈Rn×n满足以下不等式,则系统(2.1)关于(c1,c2,T,R)是有限时间稳定的. 证在定理3.1的证明过程中,由条件ω=0及ωTω ≤d,d ≥0,可令d=0,即证. 下面给出两个数值算例来说明定理3.1及定理3.2条件的有效性. 例4.1考虑如下分数阶退化线性系统: 容易得到d=ωTω=0.0014.令R=I3,可以算出xT0ETREx0=2.取γ=1,对于给定的有限时间区间J=[0,0.1](T=0.1),取c1=2,c2=5.根据假设(H1),在该例给出两个脉冲点τk=0.05k(k=1,2).应用定理3.1的条件(3.1a)、(3.1c),可以通过Matlab找到P1,P和Q如下 并得到λmax(Q)=3.7144,λmax(P1)=2.5090,λmin(P1)=1.8368.以下只需验证定理条件(3.1b), 故系统(4.1)关于 是有限时间稳定的. 例4.2考虑如下分数阶退化线性系统: 显然有d=0.为此应用定理3.2,令R=I2,容易算出xT0ETREx0=1.取对于给定的有限时间区间J=[0,0.1](T=0.1),取c1=1,c2=21.同例4.1,给出两个脉冲点τk=0.05k(k=1,2).应用定理3.2的条件(3.10a)、(3.10c),可以通过Matlab找到P1,P如下 并得到λmax(P1)=3.7830,λmin(P1)=0.9392.以下只需验证条件(3.10b), 故系统(4.2)关于(c1=1,c2=21,J=[0,0.1],R=I2)是有限时间稳定的.






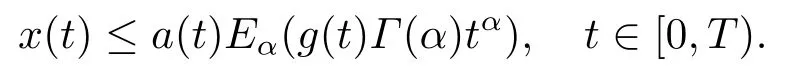




3.主要结果




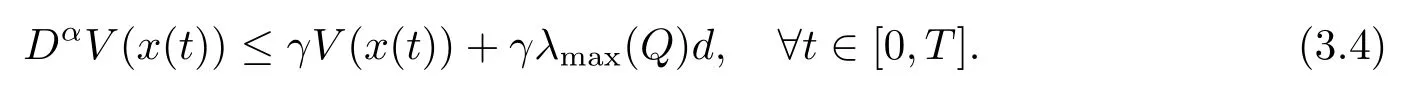







4.数值算例