石墨烯纳米带导热的分子动力学模拟
吴 霜, 王继芬,, 王绪哲, 谢华清
(1. 上海海事大学 商船学院,上海201306;2. 上海第二工业大学 理学院,上海201209)
0 前言
石墨烯作为一种新型二维纳米材料自2004年[1]发现以来,在电学、机械、光学及电化学方面都表现出独特的性质。由于其高载流子迁移率[2]、高导热率[3-5]、超高杨氏模量[6], 在传热[7]、光电[8]、传感器以及能量存储领域都有巨大的应用前景。目前在石墨烯导热方面的研究方式有实验测试、模拟和理论研究。实验方面主要研究石墨烯复合材料导热性能[9-11]和复合石墨烯的纳米流体[12-13]。分子动力学作为模拟研究微纳尺度材料的重要方式之一,广泛应用于石墨烯和类石墨烯二维材料的研究。
Azizinia 等[14]利用非平衡分子动力学的方法研究镀镍涂层对石墨烯导热性能的影响,研究结果表明涂层比增加到0.5%时,热导率降低了40%,但涂层比为2%时热导率趋于恒定值。Senturk 等[15]使用分子动力学模拟了氮掺杂对扶手型石墨烯热导率的影响,模拟表明吡啶氮掺杂热导率最高,吡咯氮掺杂热导率最低。此外模拟结果还表明掺杂在SW-1缺陷中心位置的石墨烯热导率要高于边缘位置的热导率。Ong 等[16]采用分子动力学模拟和非平衡格林函数的方式研究石墨烯-SiO2界面传热, 结果表明,电导界面大部分受低于20 z 弯曲声子模的影响,且共振机制主导了界面的声子传输。Chinkanjanarot等[17]利用分子动力学和微观力学模拟石墨烯纳米片(GNP)/脂环族环氧树脂(CE)复合材料的热导率,研究不同分散率纵横比的GNP 对复合材料热导率的影响。结果表明,GNP/CE 复合材料的导热率随着GNP 含量、分散度和纵横比的增加而增大,并通过实验验证了模拟正确性。
本文基于分子动力学中非平衡模拟的方法计算石墨烯热导率,研究几何尺寸和温度对锯齿型和扶手型石墨烯导热率的影响。
1 模型建立和计算方法
1.1 模型建立
建立扶手型石墨烯纳米带(AGNRs) 和锯齿型石墨烯纳米带(ZGNRs) 物理模型, 如图1 所示。GNRs 长20 nm、宽4 nm。
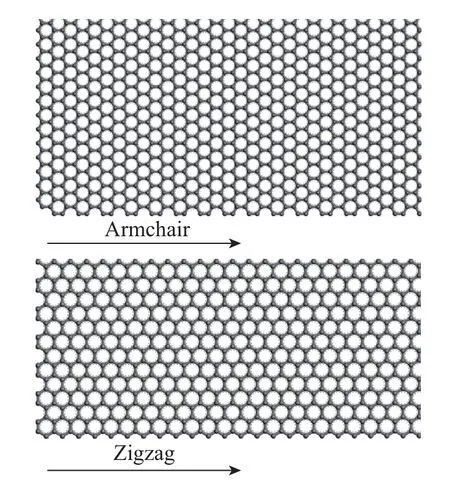
图1 AGNRs 和ZGNRs 模型Fig.1 Models of AGNRs and ZGNRs
1.2 势函数的选取和模拟方法
采用tersoff 势函数描述C–C 原子间的相互作用,其原子间交互作用总和E 的表达式为:
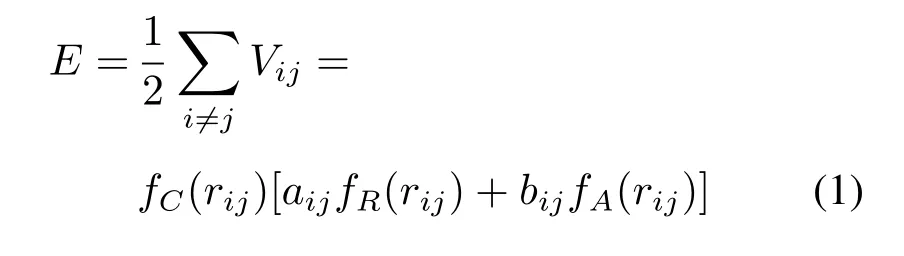
式中: Vij为原子i 和j 间的键能;rij为原子间平衡距离; fR为排斥力作用; fA为引力作用; aij和bij分别为排斥和引力作用系数;fC为光滑的分段函数,其表达式为:
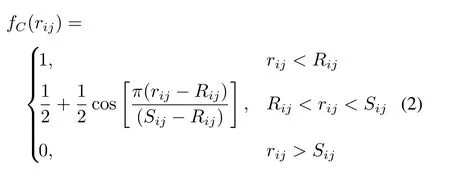
式中: Rij为i、j 原子间距; Sij为势能的截至半径; 函数fC可以使得原子距离较远时相互作用趋近于零。
本文采用分子动力学中的非平衡动力学模拟(NEMD)方式,基于傅里叶公式计算石墨烯热导率:
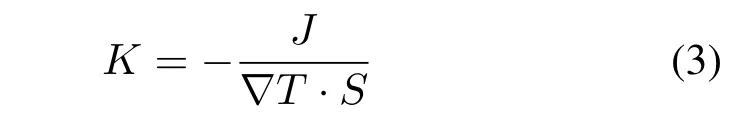
式中: J 为热流方向横截面积内的热流密度; ∇T为温度梯度; S 为截面面积。本文中的厚度均取为0.24 nm(石墨烯层间范德瓦耳斯力作用距离)。
LAMMPS (大规模原子分子并行模拟器) 中采用动量交换的方式实现热流,即通过中间原子与两端原子相互交换动能实现温度梯度和热流的产生,如图2 所示。所以石墨烯导热系数可表示为:

式中: m 为原子质量; VH和VC分别为热端最高温原子速度和冷端最低温原子速度; t 为交换原子速度的时间; 分母中2 是由于热流方向两个方向, 大小相等。

图2 NEMD 计算原理图Fig.2 NEMD calculation schematic
1.3 模拟过程
先通过MEDEA 建立物理模型, 系统能量最小化后转至分子动力学计算热导率。采用的积分方法为速度-Verlet 法, 时间步长设定为0.5 fs。采用Nos´e-Hoover 控温法,在NVT 系综下对所有的原子进行弛豫,并利用NEMD 方法形成热流。在系统的状态平衡之后(约为10 ns 后),统计拟合求得石墨烯的∇T。本文沿X 方向将石墨烯带划分为50 块,分别交换第1 和第26 块原子动能,从而形成冷端和热端如图2 所示。对系统施加N 步后使系统形成稳定热流, 统计石墨烯带划分后各块的温度。温度计算采用如下公式:
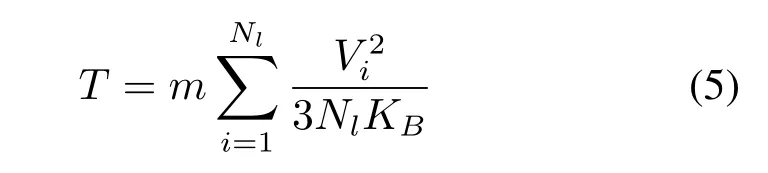
式中: m 为原子质量;Vi为第i 个原子的速度;Nl为原子总数;KB为玻尔兹曼常数。通过对冷、热端中间区间温度的线性拟合可以获得温度梯度,从而进一步得出导热系数。
2 模拟结果分析和对比
2.1 温度和手性对纳米带导热系数的影响
在温度为300 K 时, 长20 nm、宽4 nm 的AGNRs 各块温度分布图如图3 所示。通过对两侧温度的线性拟合,取两侧∇T 的平均值为。从图3 可以看出,X 方向的左右、中间区域出现温度跳跃的现象,这是由于本文选用的石墨烯模型尺寸远小于石墨烯平均声子自由程的距离,所以热端和冷端附近会产生声子散射, 在左右和中间的热端、冷端附近出现温度跳跃的现象。
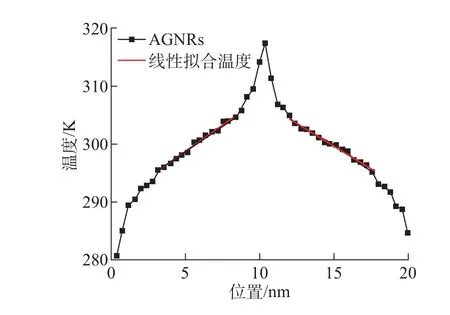
图3 AGNRs 温度分布Fig.3 Temperature distribution of AGNRs
通过模拟计算可以得出在300 K 时AGNRs 的导热系数为133.58 W/(m·K),而ZGNRs 几何尺寸温度相同,导热系数为156.45 W/(m·K)。因此可以通过改变初始温度,研究温度变化对ZGNRs 和AGNRs导热系数的影响。模拟选用长20 nm, 宽4 nm 的ZGNRs 和AGNRs, 模拟温度为200∼600 K 的热导率变化如图4 所示。可以看出温度升高,GNRs 导热系数降低。在相同的温度下,ZGNRs 热导率均高于AGNRs。因为石墨烯导热传递的方式主要为声子传热,热导率计算公式为:

式中: C 为比热容;l 为声子自由程; v 为声子速度。由于锯齿形方向的声子速度高于扶手型方向的声子速度,因此ZGNRs 的热导率要高于AGNRs 的热导率。随着温度升高,声子碰撞加剧,声子自由程降低,热导率降低。
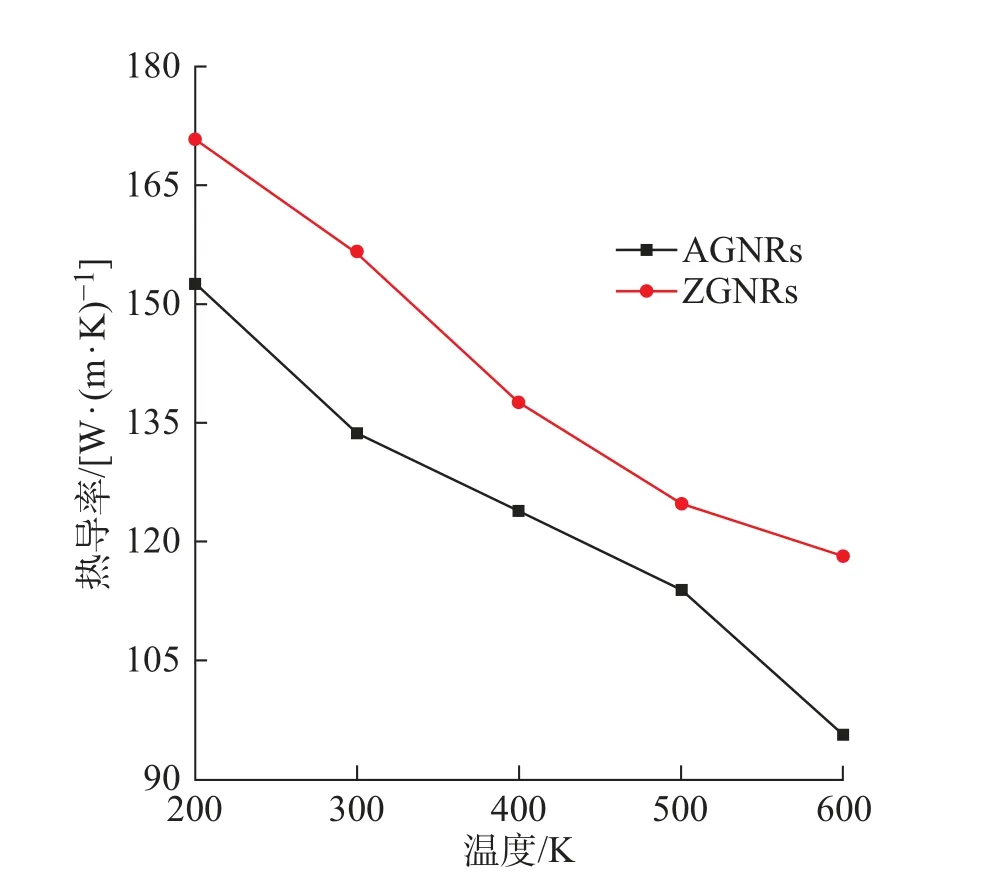
图4 随温度变化的ZGNRs 和AGNRs 的热导率Fig.4 Thermal conductivity of ZGNRs and AGNRs with temperature
2.2 几何尺寸对GNRs 导热系数的影响
2.2.1 长度对GNRS 导热系数的影响
研究模拟长度对导热系数的影响时选择了宽度为4 nm 的AGNRs。温度设定为300 K。长度分别设定为10、20、30、35、40 nm, 模拟结果如图5 所示。结果表明, 热导率随长度的增加而线性增长, 并没有出现收敛和极值的情况。热导率从10 nm 时的78.58 W/(m·K) 增加至长度为40 nm 时的226.43 W/(m·K),对比图5 中宽度为5 nm 的AGNRs 的热导率[18],可以看出模拟计算出的热导率也随长度的增加而增加,进一步验证了模拟的准确性。由于分子动力学模拟的长度远小于GNRs 的平均自由程775 nm[19], 声子处于弹道发射区域,所以随着模拟长度的增加, 热导率不断线性增加。同时由于模拟系统尺寸限制,导致声子平均自由程较小,模拟热导率低于实际的实验测量。
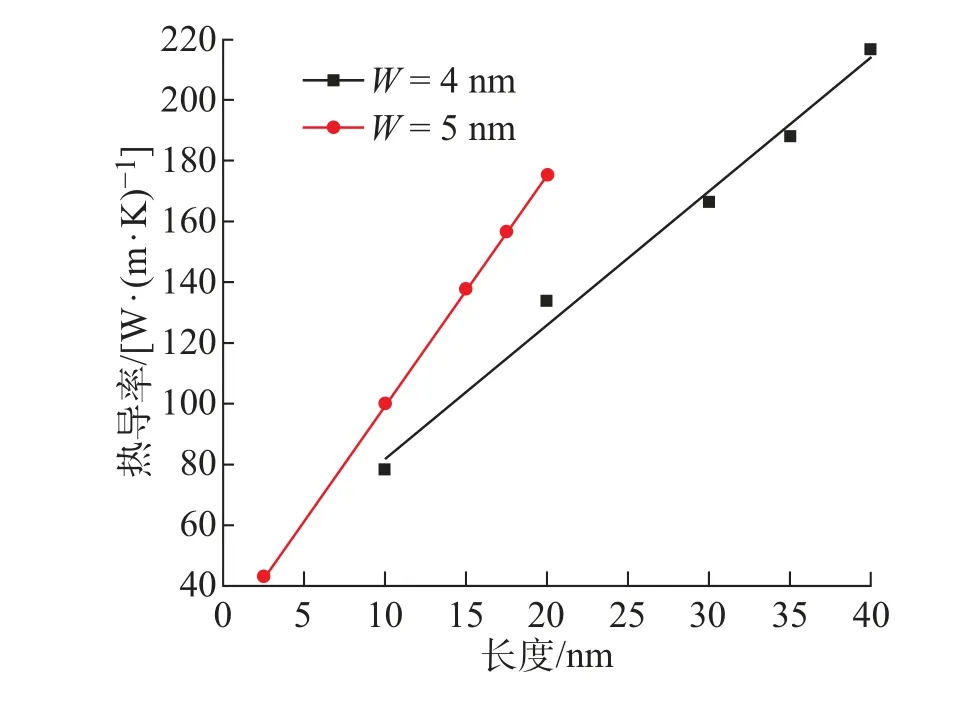
图5 热导率随长度变化Fig.5 Variation of thermal conductivity with length
2.2.2 宽度对GNRs 导热系数的影响
选择长度为20 nm 的AGNRs, 温度设定为300 K。模拟的宽度分别为4、10、15、17、20 nm,热导率的模拟结果如图6 所示。与图6 中唐恺[20]计算的长度为30 nm 的AGNRs 的热导率变化规律相同,模拟热导率也随宽度的增加而升高,进一步验证了长度为20 nm 的AGNRs 热导率的准确性。
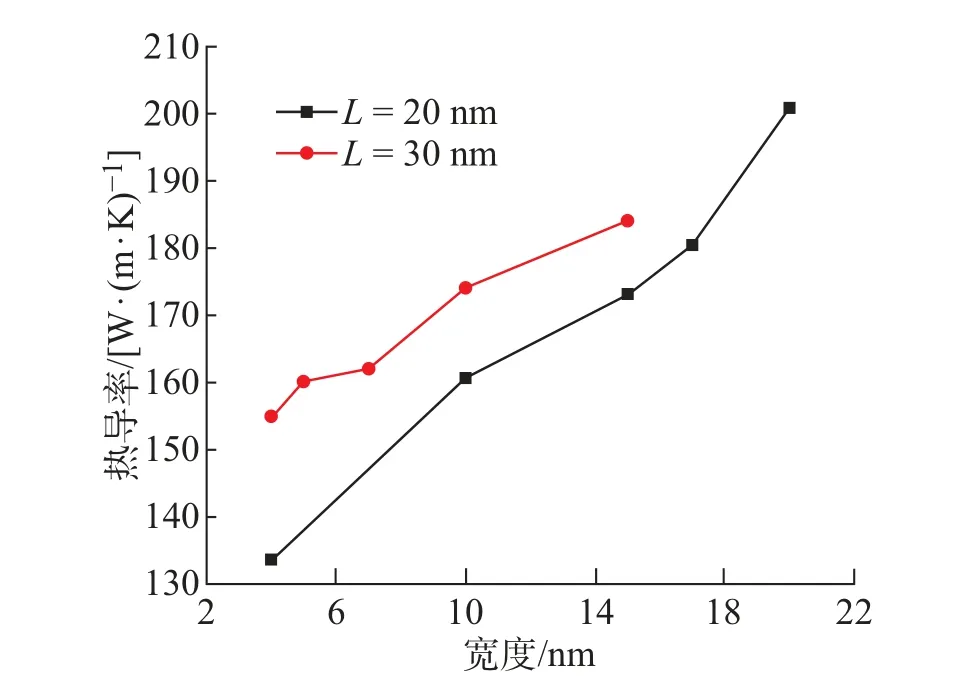
图6 AGNRs 热导率随宽度变化Fig.6 Thermal conductivity variation of AGNRs with width
造成热导率随宽度的变化而变化的主要原因是边界散射。传热主要是依靠能量较低的声子来进行传递, 而边界散射会严重影响能量较低的声子。随着宽度的增加, 边界散射作用减弱同时声子的态密度提高,因此石墨烯的热导率随着宽度的增加而增加。
2.3 几何形状对GNRs 热导率的影响
选择长为8.45 nm、高为4.8 nm 的直角三角形非对称石墨烯,模型如图7 所示。图中左右边界原子为固定不动的边界, 右侧区域为热源, 左侧区域为热汇, 箭头方向为热流方向从右到左。通过靠近固定边界区域动能的交换形成热流,定义X 方向从右到左为正向,从左到右为反向。由于结构为非对称性,采用Jund 法计算热导率,先在NVT 系综下对除去边界的原子进行弛豫,之后选择NEMD 中Jund法计算热导率。
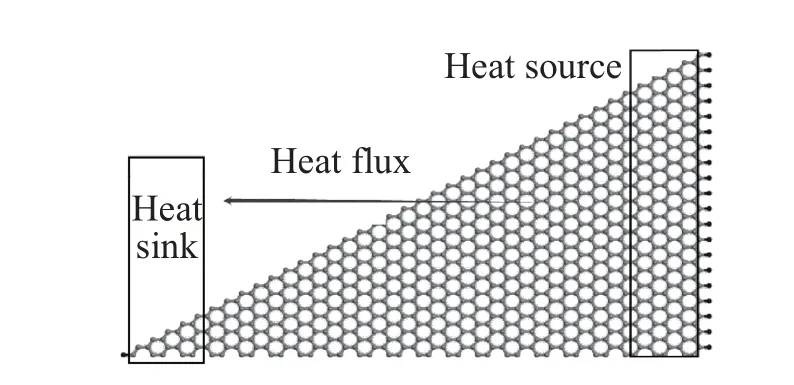
图7 三角形GNRs 模型Fig.7 Model of triangle GNRs
由于三角形石墨烯截面积在不断变化,所以内部温度梯度将不再是常数。温度300 K、热流方向为正向时,三角形GNRs 内部温度分布如图8 所示。可以发现在结构两侧存在温度跳跃的现象,这是由于声子散射造成温度突变。因此拟合时跳过两侧温度跳跃的区间, 对中间的区间进行非线性拟合。拟合得到温度T 和X 的函数,其表达式为
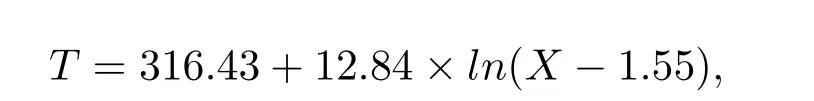
式中,X 为温度区域到左侧边界的距离。经过进一步计算得到300 K 时正向三角形GNRs 的热导率为228.43 W/(m·K)。
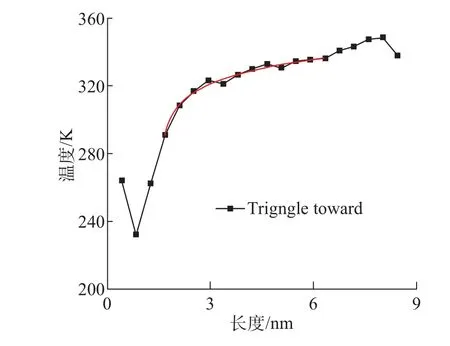
图8 三角形GNRs 温度分布图Fig.8 Temperature distribution of triangle GNRs
改变热流方向, 热导率将发生变化。为了进一步研究整流效应,定义整流系数
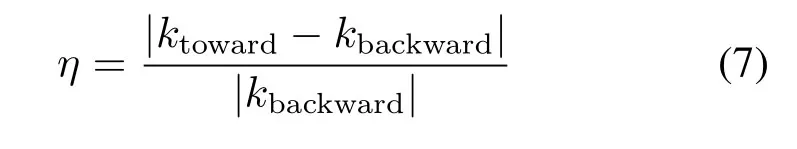
式中: ktoward为热流正向时热导率;kbackward为热流反向时热导率。整流系数越大,整流效应越明显。通过改变不同的温度研究整流系数的变化,模型仍为直角三角形模型。温度分别为300、350、400、450 K,三角形GNRs 热导率模拟结果如图9 所示。图10 所示为随温度变化的整流系数图, 图中I 为Hu[21]对三角形AGNRs 计算结果,II 为根据图9 所绘的热导率。模拟结果表明三角形GNRs 存在热整流效应,即随着温度的升高整流系数降低, 整流效应下降。本文模拟所选用的尺寸比文献[21]中的长,整流系数较低, 这也符合Hu 关于整流系数随长度的增加而降低的结论。造成这一现象的主要原因为声子频谱和能量谱耦合的非对称性[22],声子频谱随温度的升高而升高,声子传输通道增多,则相同热流下温度梯度越高、热导率越大。在正向热流下,声子频谱的叠加较多,为声子传输提供更多的通道,相同热流下温度梯度更高、热导率越大。因此,正向热导率较反向高,形状对石墨烯热导率存在影响,非对称结构存在热整流效应且随着温度的升高而降低。
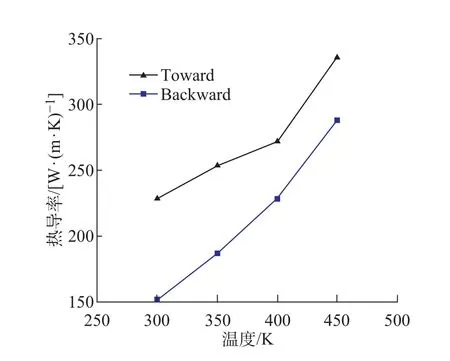
图9 三角形GNRs 热导率随温度变化Fig.9 Thermal conductivity of triangle GNRs varies with temperature
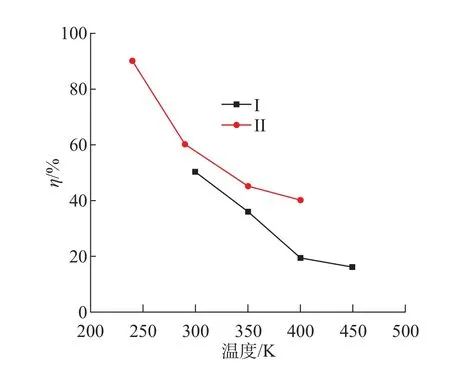
图10 整流系数随温度变化Fig.10 Variation of thermal rectification factor with temperature
3 结 论
基于分子动力学原理, 对影响GNRs 热导率的几何尺寸、手性和温度进行了研究。模型建立及优化基于MEDEA 软件,模拟计算采用NEMD 方法研究GNRs 的热导率,结论如下:
(1)采用NEMD 方法计算了GNRs 热导率。模拟结果表明GNRs 的热导率随温度的升高而降低。这是由于温度升高声子自由程降低, 导致热导率降低。
(2) 模拟结果表明, GNRs 热导率与手性有关。由于ZGNRs 锯齿方向的声子传递速度高于AGNRs扶手型方向,因此ZGNRs 的热导率高于AGNRs。
(3)GNRs 作为低维材料,其热导率受几何尺寸影响较为明显。其他条件均相同的情况下, 热导率随长度和宽度的增加而近似线性增长。
(4)形状影响GNRs 的热导率。三角形GNRs 具有热整流效应,随着温度的提升整流效应降低。

