嵌入式相变材料对热电发电器件性能的影响
田园园, 刘安邦, 张梦君, 王俊丽, 谢华清, 吴子华, 王元元,b
(1. 上海第二工业大学a. 环境与材料工程学院;b. 资源循环科学与工程研究中心,上海201209;2. 南京理工大学 能源与动力工程学院,南京210014)
0 引言
热电器件(thermoelectric generator, TEG) 能够直接将热能转化为电能,以其体积小、操作简单、无运动部件、寿命高、运行成本低等优点[1-2]被广泛应用于航空航天[3]、太阳能光热发电[4]、余热和废热利用[5-6]以及海上航行[7]等领域。传统的TEG由热端、冷端、p 型半导体材料和n 型半导体材料串联而成, 为冷、热端施加不同的温度在热电臂内形成温度梯度, 以此产生电能。决定TEG 性能的主要因素是热电材料性能和热电模块结构[8]。虽然学者们已经做了大量研究, 但TEG 的转换效率始终只有10% 左右[9-11]。转换效率低是目前TEG应用过程中亟待解决的问题。为了提高TEG 的热电转换效率, 首先要提高热电优值(ZT)[8,12-13], 优化TEG 的几何尺寸[14-15],稳定热源温度[16-17]。热电发电器件的应用环境决定热源会有强烈波动,因此稳定热源温度尤为重要。相变材料(phase change material,PCM)以其高相变潜热、高密度、吸收和释放热量时温度稳定等优点[18],被应用于热电领域以稳定热端温度,有效提高热电发电系统的热电转换效率。Carneiro 等[7]利用海洋温度梯度,应用TEG为水下自主航行器提供动能, 引入PCM 储存热能并稳定热源温度。结果表明,使用PCM 的热电发电系统可以提供更多的动能。Kiziroglou 等[19]探究了PCM 对无线飞机传感器热电发电系统连续发电性能的影响,实验结果表明,使用PCM 可以为无线飞机提供足够的电能。Kiziroglou 等[20]通过数值模拟和实验相结合的方法,探究了PCM 的储热功能在热电采暖中对热电发电器件发电性能的影响。结果表明,使用PCM 能够很好地稳定热源温度,极大地提高TEG 的总发电量。Cui 等[21]建立了一种新型的光伏-相变-热电(PV-PCM-TE)混合系统,将PCM镶嵌在PV 模块和TE 模块之间,吸收PV 模块中多余热量的同时为TE 模块提供稳定的热能。结果表明,采用PCM 可以显著提高PV-PCM-TE 系统的性能。Altstedde 等[22]将PCM 应用于汽车热电发电器件的热端,稳定热端温度。结果表明,PCM 能较好地稳定热源温度,提高TEG 的发电性能。Atouei 等[23]设计了PCM 与TE 模块组成的热电联产两级发电系统。PCM 镶嵌在一、二级之间, 作为第一级的冷端,第二级的热端。结果表明,相比于第一级或第二级单独发电, 两级同时发电产生的电能最多。上述研究表明, PCM 能够很好地稳定热端温度,在热源停止供热后为热电发电续能, 延长TEG 的发电时长。然而,PCM 处于热源与热电发电器之间,在稳定热端温度的同时,阻碍了热源和热电发电器件热端之间的传热。基于此,Jo 等[24]提出了一种嵌入式的PCM-TEG 装置。该装置以聚二甲基硅氧烷(PDMS)为主体,内部设有空间用于存放TEG 和PCM。PCM包裹在热电臂靠近热端的周围用于吸收热源散失的热量。实验对比了有无PCM 的两种发电情况,结果表明, 包裹了PCM 的装置具有较好的发电性能。Liu 等[25]在前者的基础上研究了PCM 的尺寸(横截面和高度) 对单腿TEG 发电性能的影响。结果表明, TEG 的总发电量随着PCM 横截面和高度的增加而增大。然而,以上工作忽略了PCM 体积相同时,PCM 的尺寸对热电发电器件性能的影响。基于热源与热电发电器件热端直接接触以保证热端传热的思路,本文设计了嵌入式的PCM-TEG 系统,将PCM 包裹在热电臂靠近热端的周围,探究了热源停止供热后的一定时间内,相同体积不同长度的PCM对TEG 发电性能的影响,以探究PCM 包裹热电臂的长度的优化值。
1 研究模型与方法
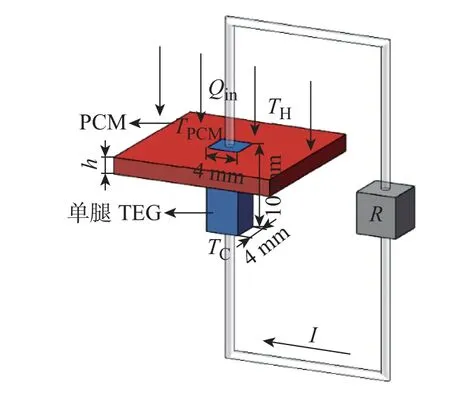
图1 PCM-TEG 模型图Fig.1 The schematic of PCM-TEG
图1 为PCM-TEG 系统的示意图, 其由单腿TEG 和镶嵌在热电臂周围的PCM 组成。热端和冷端的温度分别为TH和TC, 外接电阻为R。本文采用的PCM 为硬脂酸, 其热性能参数如表1 所示[26]。硬脂酸作为有机储能材料具有化学稳定性好、相变潜热大、成本低等优点。PCM 的初始温度为373 K。本研究中,基于热电发电器件的尺寸,设定PCM 的体积为800 mm3,宽度与厚度相同,PCM包裹热电臂的高度为h(1≤h≤5 mm)。为了更好地解释研究结果, 引入了热电臂的冷热端温差∆T(∆T = TH−TC)。PCM-TEG 系统中的热电材料为常见的低温热电材料p 型Bi0.5Sb1.5Te3[27]。当TEG 冷、热两端存在温度差(TH> TC) 并在电路中串联一个负载时, 由于Seebeck 效应闭合回路中产生电流I。计算中, 采用了两个假设: (1) 环境和PCM-TEG 系统之间不存在热交换, 即真空条件下;(2)PCM 与热电臂之间的接触热阻忽略不计。这两个假设不会影响本文的主要结论。

表1 硬脂酸的性能参数[26]Tab.1 The properties of stearic acid [26]
在PCM-TEG 系统中, 应用热力学第一定律建立瞬态导热问题的控制方程[7,28-29]
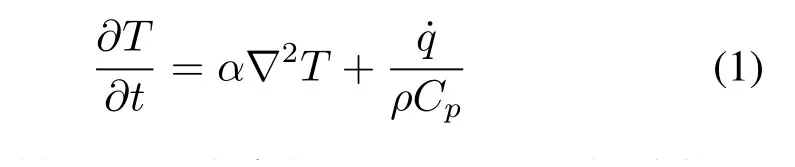
式中: t 为时间, s; T 为空间(x,y,z) 和t 相关的温度,K;∂T/∂t 为某一点温度相对于t 的变化率;α 为热扩散系数; ˙q 为单位体积内热量的生成率;ρ 为密度,kg/m3; Cp为恒压比热容,J/(kg·K)。∇为揭示物体温度梯度的拉普拉斯算子。
利用Galerkin 加权残差法对体积进行积分[30],同时考虑边界条件(温度、热流和对流的时空依赖性) 和形状函数的替换[31], 通过ANSYS 进行有限元分析。式(1)可以写成下列矩阵形式:
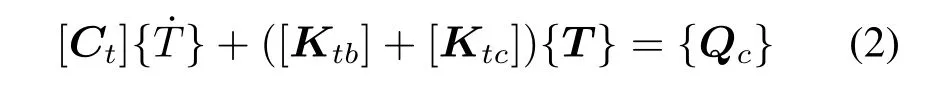
式中: t、b 和c 分别为时间、扩散系数和对流表面;[Ct] 为比热矩阵, J/(kg·K); { ˙T} 为每个节点的温度变化率,K/s; [Ktb]和[Ktc]分别为扩散导热矩阵和对流表面导热矩阵; {T} 为节点温度, K; {Qc} 为对流表面热流矢量。基于初始参数和材料特性, 在ANSYS 中采用Newton-Raphson 算法求解离散的非线性方程,在给定的时间间隔内求解{Qc}[32]。
在降温过程中PCM 经历液相到固相的转变,即凝固过程。在ANSYS 中,利用焓模型考虑了冷却过程中相变释放的潜热能,并将焓(H)定义为温度的函数,由所用材料的比热(C)、ρ 和T 来表示[33]:
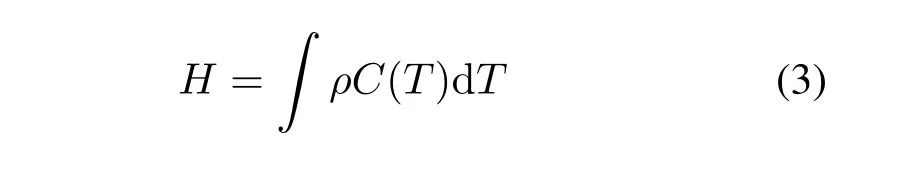
式(3) 包含了3 种状态的PCM 相对于T 的H值[34]。
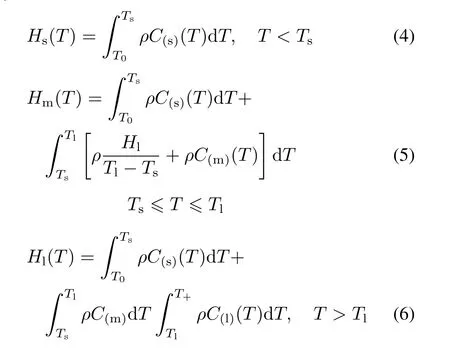
式中: Hs、Hm、Hl分别为固体、固液混合态和液体PCM 相对于T 的焓值,J/m3;Hl为相变潜热,kJ/kg;Ts为固相线温度,K;T0、Tl和T+分别为下限温度、液相线温度和上限温度,K;C(s)、C(l)和C(m)分别为固体比热、液体比热及固体和液体的平均比热,J/(kg·K)。
整合并对式(4)∼(6)进行积分可得[33]:
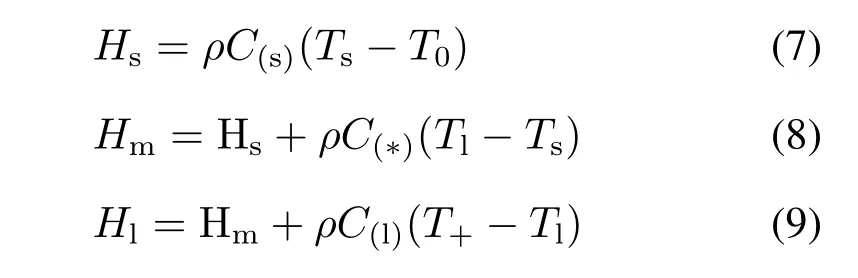
式中,C(∗)为固液混合区比热容,J/(kg·K)。可定义为
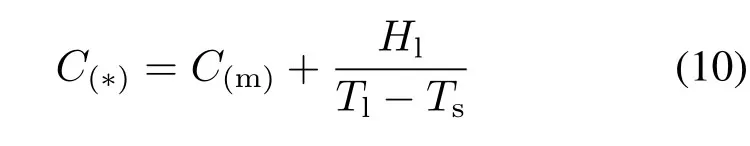
式(7)∼(9) 定义了温度界限后, 可用来定义PCM 的H 与T 的关系曲线。通过ANSYS 软件的Transient-Thermal 模块, 利用以上焓法公式模拟PCM-TEG 系统在热源停止供热后, PCM 做为热源继续为TEG 供热的一段时间内,系统随时间变化的温度分布。将获得的TEG 的瞬态温度分布数据导入ANSYS 软件的Thermal-Electric 模块, 利用有限元方法计算出TEG 随时间变化的输出电流(I,mA)和输出电压(U,mV),继而得到随t 变化的输出功率(P,mW)和总产能(E,mJ)
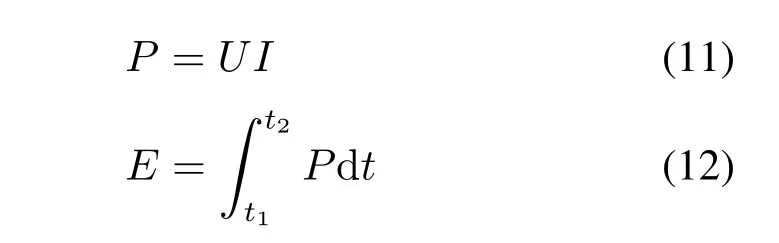
2 结果与讨论
在PCM-TEG 系统中,热电臂与热源直接接触,由于kPCM< k热电臂,热量优先在TEG 模块中传递,相变模块吸收没有被热电发电器件吸收的热量并储存。当热源停止供热后, PCM 作为热源继续为TEG 供热。本文研究了热源停止供热后,PCM 作为热源继续为TEG 供能的一定时间段内,体积不变的PCM 包裹热电臂的高度变化时对TEG 发电性能的影响。在计算中,假设PCM 温度为373 K 时热源停止供热,冷端温度固定为283 K,外接电阻与内阻相等,固定为15 mΩ。为了研究PCM 包裹热电臂的高度h 对TEG 发电性能的影响,将h 固定在1∼5 mm间变化。
图2 为PCM 的温度随着时间变化的性质。由图2 可知, PCM 包裹热电臂的高度越长, 相变阶段维持的时间就越短, 这是因为假设PCM-TEG 系统与外界无热量交换、同时忽略了PCM 与热电臂之间的接触热阻,PCM 储存的热量全部用来发电所造成的。因此,PCM 与热电臂的接触面积越大,热量传递就越快。图3 为热电发电器件的性能随时间变化的性质。从图3(a)∼(c)可以看出,在PCM 的相变阶段,PCM 包裹热电臂长度越长,PCM-TEG 系统的瞬时U、I 和P 越大且下降得越快。由图3(d)可以清晰地看出, 热源停止供热后的14 700 s 内, 当PCM包裹热电臂的长度h = 4 mm 时, 即被PCM 包裹的长度与总长度的比值为40%时, PCM-TEG 系统产生的电能最多。且此时产生的电能比h=1 mm时增加了42.39%。即在保持PCM 体积一定的情况下, PCM 包裹热电臂的长度存在最优值,可以大幅提高热电发电器件的输出电能。同时注意到, 与不使用PCM 相比, 取PCM 包裹长度最优的条件(h = 4 mm)时,输出电能增加了76.06%。为了探究PCM-TEG 系统的瞬时U、I 和P 随着时间变化的原因,探究了热电臂的∆T 与时间的变化关系,如图4 所示。由图可知, h 越大, ∆T 在相变平台处的值越大,且下降越快;h 越小,∆T 在相变平台处的值越小, 且下降越慢。热电臂的∆T 随时间的变化是导致PCM-TEG 系统产生的总能量随着h 变化有最大值的重要原因。由此可见,PCM 的使用能够提高热电发电系统对热能的利用率,且在使用的PCM 的体积一定时,需要优化PCM 包裹热电臂的长度以提升热电发电器件的输出热能。
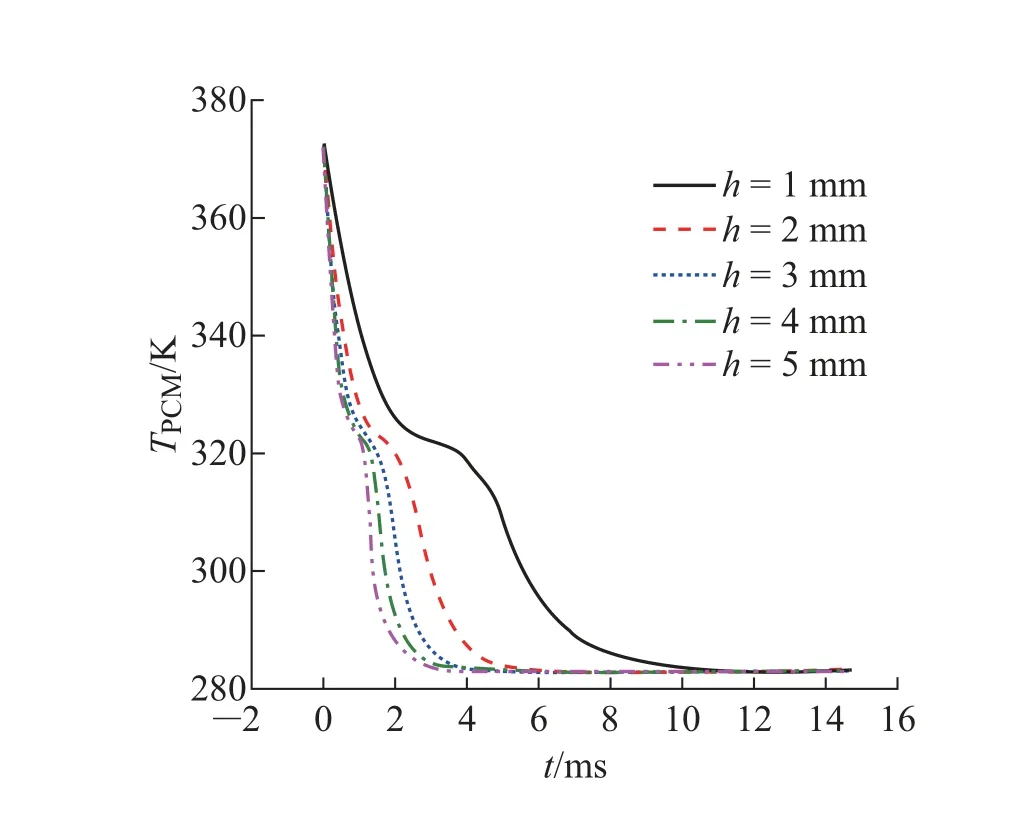
图2 PCM 随时间变化的温度Fig.2 The temperature of PCM varies with time
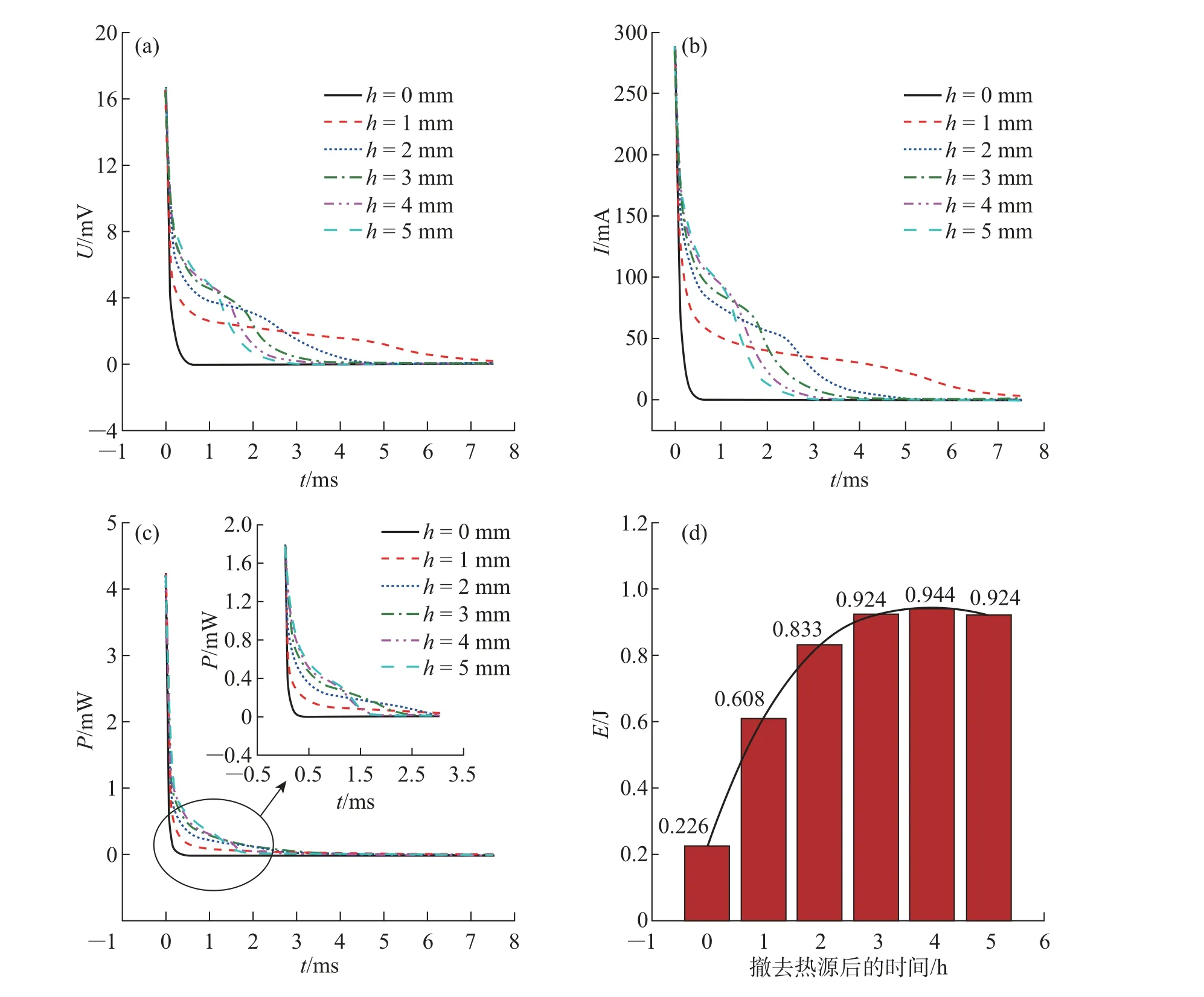
图3 PCM-TEG 系统的(a)U、(b)I、(c)P 及(d)撤去热源后的14 700 s 内产生的总能量随时间变化的性质Fig.3 (a)U,(b)I,(c)P and(d)the total energy within 14 700 s after the heat source removed of PCM-TEG system varies with time
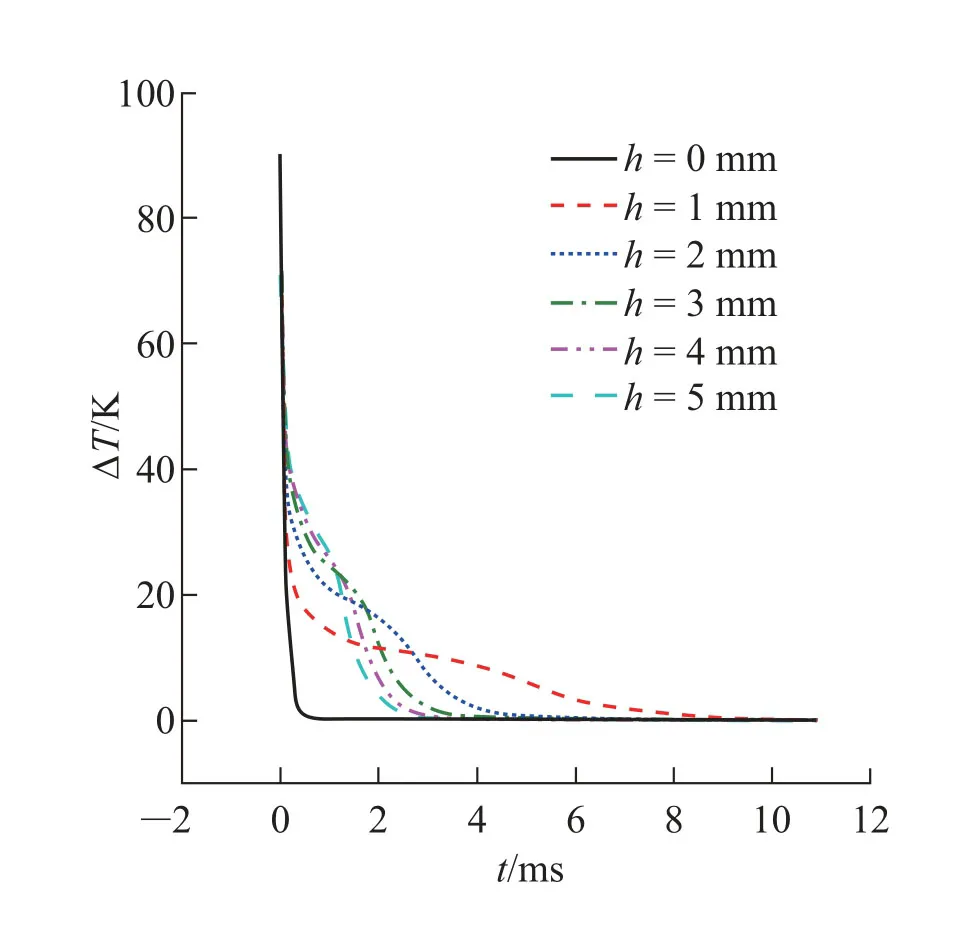
图4 PCM-TEG 系统中电臂冷热端的∆T 随时间变化的性质Fig.4 The ∆T between the hot-and cold-ends of the thermoelectric leg varies with time in the PCM-TEG system
3 结 论
PCM 与热电发电器件耦合, 能够极大地提高TEG 对热能的利用率。本文设计了一个嵌入式的PCM-TEG 系统,将PCM 镶嵌在TEG 的热电臂靠近热端的外围。利用有限元方法研究了在PCM 的体积保持不变时, 改变PCM 包裹热电臂的长度对热电发电器件的性能的影响, 并且与不采用PCM 的热电发电系统进行了对比。结果表明,使用PCM 有效提高了TEG 的发电性能。撤去热源后,PCM-TEG系统产生的总电能随着PCM 包裹热电臂的长度变化且存在最大值。当h = 4 mm 时,PCM-TEG 系统产生的电能最多,与h = 1 mm 时相比,电能增加了42.39%。同时, 与不使用PCM 相比,当采用了最优的PCM 包裹条件时, 热电发电器件的输出电能增加了76.06%。因此, PCM 的应用极大地提高TEG对热能的利用率, 并且PCM 包裹热电臂的长度在PCM 体积保持不变的情况下存在最优值。

