氢原子在少周期强激光场中阈上电离的电子波包干涉图像

郭志坚，孙 乾

(陇东学院 电气工程学院，甘肃 庆阳 745000)

1 引 言

原子阈上电离(Above-Threshold Ionization,ATI)是强激光场与物质相互作用的一个基本过程[1]。阈上电离发生的过程可以分为多光子电离(γ>1)和隧穿电离(γ<1)两种电离机制。根据经典的三步模型理论，在隧穿电离机制下，电子在激光场作用下，有一定概率返回母核发生重散射，即高阶阈上电离[2]。电子波包之间的干涉效应在强场电离中是一个非常重要的概念，末态动量相同的电子波包会发生干涉效应，干涉理论可以用来分析强场电离中的许多现象[3-6]。根据产生电子波包的时间间隔，可将电子波包分为周期间干涉(电离间隔为一个周期之外)和周期内干涉(电离间隔为一个或多个周期)，周期间干涉和周期内干涉的相互作用形成了阈上电离光电子能谱和二维动量谱的典型特征。近几年，学者们利用鞍点近似方法、经典轨道蒙特卡洛方法及量子轨道蒙特卡洛方法等对电子波包干涉进行了大量的研究[7-10]。

由于红外激光技术的快速发展，强场电离已经可以在深度隧穿电离机制下发生，随着人们对强场电离的深入研究，逐渐发现库仑势以及电子与母核发生的再散射对光电子能谱以及二维动量谱有着非常重要的影响。在深度隧穿电离机制下，实验中发现在红外激光场作用下光电子能谱将在低能处产生尖锐的峰，即低能结构(Low-Energy Structure,LES)[11]，而经典的强场近似(Strong Field Approximation,SFA)模型无法重现出该结构。一些人认为该结构是在长程库仑势作用下电子与母核的再散射引起的[12-13]， LES的出现不依赖于靶原子或分子，但是与激光强度、波长以及脉宽有很大的关联，对此至今仍然没有合理的解释。另外，在光电子二维动量分布中，在低能部分的扇形结构也被认为是由库仑势引起的，在SFA基础上考虑库仑势效应的Coulomb-Volkov近似(Coulomb-Volkov Approximation,CVA)方法能够较好地重现出该结构。

本文采用了一种SFA和CVA结合时间窗函数(限制电离时间)来得到电子波包干涉的方法，从电子波包干涉的角度出发，研究了在隧穿电离机制下(γ=0.5)库仑势以及电子再散射对少周期原子阈上电离二维光电子动量谱的影响。首先通过SFA方法和CVA方法的对比，发现库仑势在电子波包干涉中起到非常重要的作用，在库仑势的影响下，电子波包周期内干涉和周期间干涉共同作用，形成了二维动量谱中的扇形条纹结构。另外，采用数值求解TDSE(Time-Dependent Schrodinger Equation)方法计算了不同脉宽下氢原子的二维动量谱，发现二维动量谱中存在特殊的径向条纹，在2 cycles脉冲下的径向条纹尤其明显，随着脉宽增加，周期内干涉作用使得这些径向条纹变得模糊。通过进一步分析发现这些径向条纹是再散射电子波包之间的干涉引起的。

2 基本方法

2.1 TDSE方法

在单电子近似下，强场中电子的波函数可通过求解下面的含时薛定谔方程得到：

Hi(t)]ψ(r,t) ,

(1)

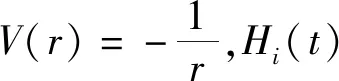
E(t)=E0a(t)cos(ωt+φ)z.

(2)

包络函数a(t)形式如下[13]：

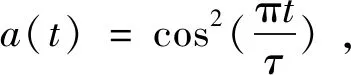
(3)

在数值计算中，随时间演化的波函数ψ(r,t)通过下面方式展开[14]：

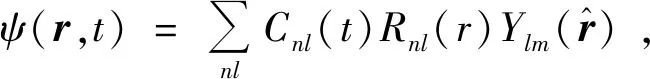
(4)

电离振幅通过投影方法得到：

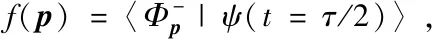
(5)

末态动量为p的自由态电子，其动量分布可通过下面方程得到：

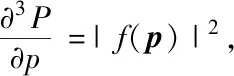
(6)

其中，P为电离几率，f(p)表示电子从基态跃迁到动量为p的末态的电离振幅。

对于线性极化的激光场，光电子二维动量谱为：

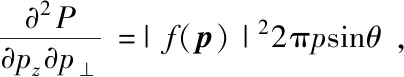
(7)

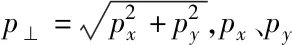
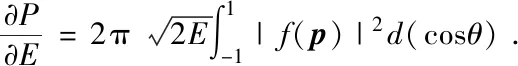
(8)

2.2 SFA方法

对于SFA方法，电子的电离振幅为：

f(p)=f1(p)+f2(p) ,

(9)

其中第一项表示直接电离部分，即SFA1：

(10)

SFA模型中，电离态用Volkov态表示，即：

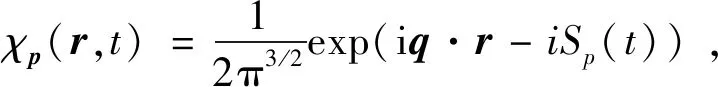
(11)

q(t)=p+A(t)，A(t)为电场矢势，Sp(t)可写作：

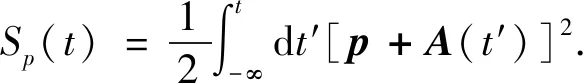
(12)

对于氢原子，基态为：

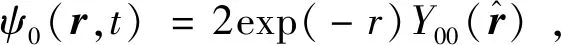
(13)

对空间部分积分之后，电离振幅为：

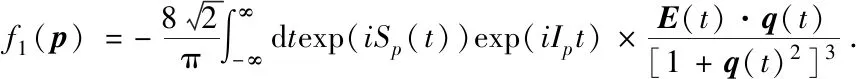
(14)

与电子再散射有关的电离振幅为(SFA2)[15]：

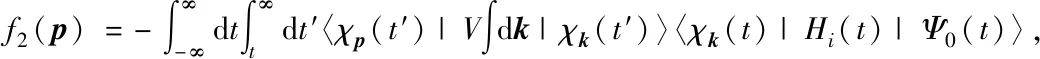
(15)

|χk(t)〉表示动量为k的Volkov态，对空间部分积分后，有：

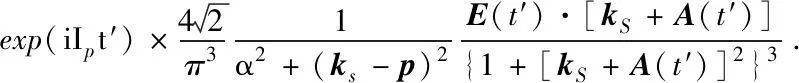
(16)

积分过程中对动量k采用了鞍点近似，kS为鞍点动量，α是为了避免积分发散引入的量，本文取α=1。

为了得到电子波包干涉图像，引入时间窗函数，其定义为[16]：

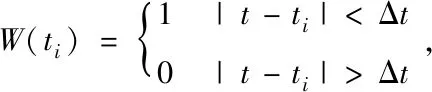
(17)

其中，ti为时间窗的中心，Δt=0.01T，T为电场的周期。电场可以写成如下形式：

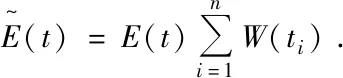
(18)

结合时间窗函数，SFA1电离振幅可以表示成：

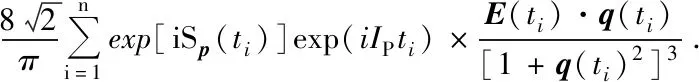
(19)

式中的E(ti)为第i个时间窗电场的平均值。

2.3 CVA方法

CVA未考虑电子的再散射情况，它在SFA1的基础上，考虑了在激光场作用下电离电子受到母核的库仑势，电子从基态到连续态的跃迁振幅为：

(20)

其中，|ψ0(t)〉为原子基态，对于氢原子仍采用式(5)的形式，|ψp(t)〉为Coulomb-Volkov态，其表达式为[17]：

ψp(r,t)=χp(r,t)cp(r) ,

(21)

库仑态cp(r)为：

1; (pr+p·r)] ,

(22)

其中，1F1为合流超几何函数。

3 结果与讨论

图1给出了模拟计算所用激光场的电场及矢势(在最大峰值处进行了归一化)，脉宽为5 fs，A、B、C为式(17)中提到的时间窗。A窗和B窗(或A窗和C窗)电离的电子具有相同的末态动量，电离间隔在一个周期之内，其电子波包会发生周期内干涉；B窗和C窗电离的电子波包会发生周期间干涉；3个时间窗都打开时，得到的是周期内干涉和周期间干涉共同作用的结果。

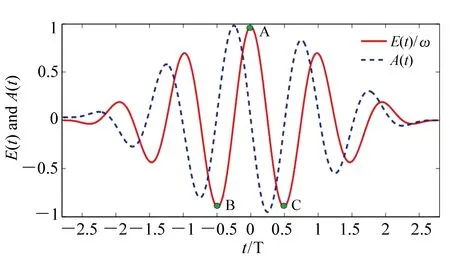
图1 激光场的电场及矢势，I=4.0×1014 W/cm2, λ=800 nm, CEP=0, Γ=5 fs Fig.1 Electric field and vector potential of laser field with I=4.0×1014 W/cm2, λ=800 nm, CEP=0, Γ=5 fs

电子波包干涉图像如图2(彩图见期刊电子版)所示。为了说明库仑势的作用，图2分别展示了SFA及CVA结合时间窗函数得到的二维动量谱。图2(a)、2(c)以及2(e)为SFA模拟结果，图2(b)、2(d)以及2(f)为CVA模拟结果。(a)和(b)为周期内干涉图像；(c)和(d)为周期间干涉图像；(e)和(f)为周期内干涉及周期间干涉相互作用的图像。

图2 氢原子电子波包干涉形成的二维动量谱 Fig.2 2D momentum spectra of H atom with EPs interferences

由于CVA方法考虑了长程库仑势，所以图2(b)的周期内干涉及图2(d)的周期间干涉图像均向阈值方向移动，低能部分的干涉条纹均出现了扭曲。图2(b)及2(d)在阈值附近均出现了径向条纹，共同形成了图2(f)中的扇状条纹；图2(e)相应位置处为垂直条纹，这充分说明二维动量谱中的扇形结构是在长程库仑势作用下，由周期内干涉和周期间干涉共同作用形成的。

图3(彩图见期刊电子版)是电子波包干涉形成的光电子能谱，图3(a)为周期内干涉能谱，可见，能谱中随着光电子能量增加，峰与峰的间隔逐渐增大；图3(b)为周期间干涉能谱，能谱中峰与峰的间隔相等，是典型的ATI峰；图3(c)是周期间干涉和周期内干涉相互作用形成的能谱，图中的蓝色曲线为图3(a)的周期内干涉能谱，通过比较可以明显地看到光电子能谱仍然保持ATI特征，但是谱线整体受到了周期内干涉的调制。

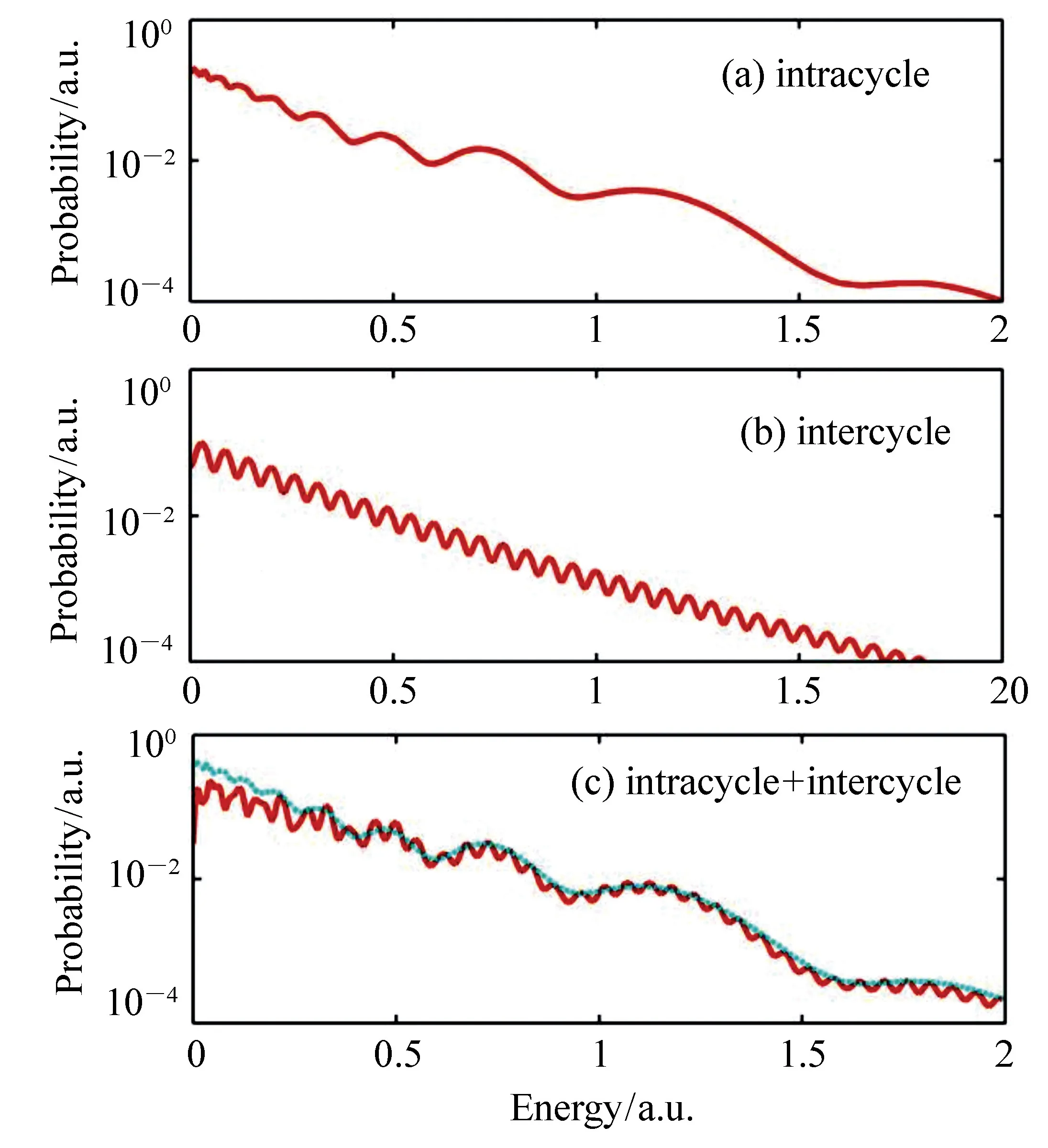
图3 CVA方法得到的电子波包干涉形成的光电子能量谱，激光参数与图1相同。(a)周期内干涉；(b)周期间干涉；(c)周期内干涉和周期间干涉相互作用的结果 Fig.3 Photoelectron energy spectra of EPs interferences by CVA under the same laser field as shown in Fig.1. (a)Intracycle interference; (b)intercycle interference; (c) intercycle and intracycle interferences

图4比较了采用SFA、CVA及TDSE方法计算得到的氢原子的二维动量谱(不设置时间窗)，激光参数与图1相同。3种方法得到的二维动量谱在整体结构上非常相似，都可以看到明显的周期内干涉条纹和周期间干涉条纹。SFA方法未考虑长程库仑势效应，在阈值附近产生垂直条纹，CVA及TDSE方法得到的是扇形的径向条纹，考虑了库仑势修正的CVA方法也未能够完全重复出TDSE的扇形结构，一些研究认为这是由于阈值附近的扇形结构不仅与库仑势作用下的直接电离有关，同时与电子跟母核的再散射有关[18]。从本文得到的结果来看，CVA方法虽然重复出了阈值附近的扇形条纹，但是扇形条纹的数目与TDSE结果仍然有明显差别，总是少于TDSE中的条纹数目，因此认为其他几条扇形条纹与电子再散射有关是合理的。此外，由于库仑势作用，3种方法得到的周期内干涉条纹位置有明显的偏移，这种现象在图5给出的能量谱中能够更直观的看到。图5(a)、5(b)及5(c)分别为TDSE、CVA和SFA模拟计算的光电子能量谱，在图中的箭头标记处为周期内干涉产生的峰，由于库仑势作用，TDSE和CVA对应的峰均向低能方向移动，其中TDSE移动较为明显。

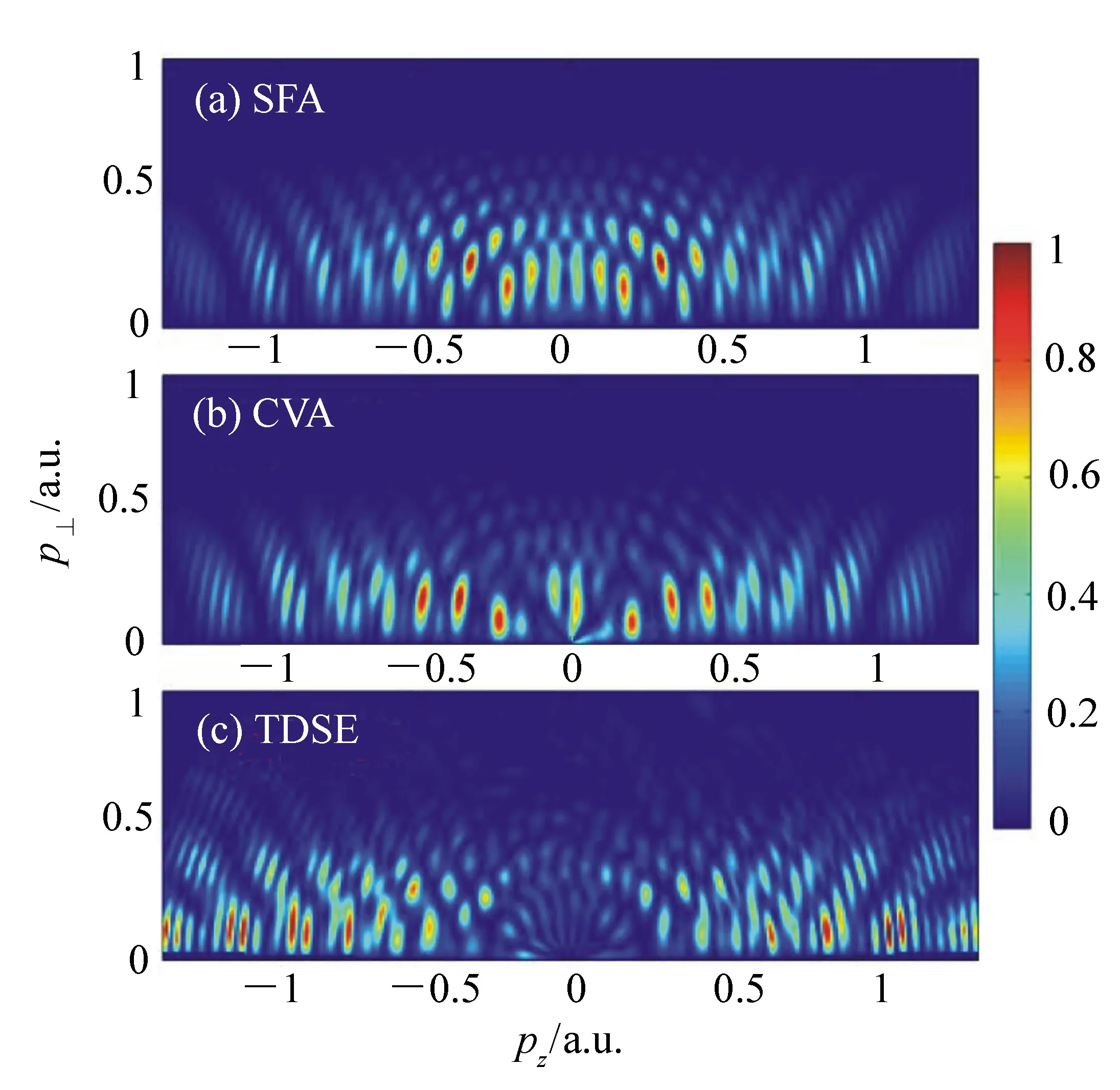
图4 H原子二维光电子动量谱，激光参数与图1相同 Fig.4 2D photoelectron momentum spectra of H atom under the same laser field as shown in Fig. 1

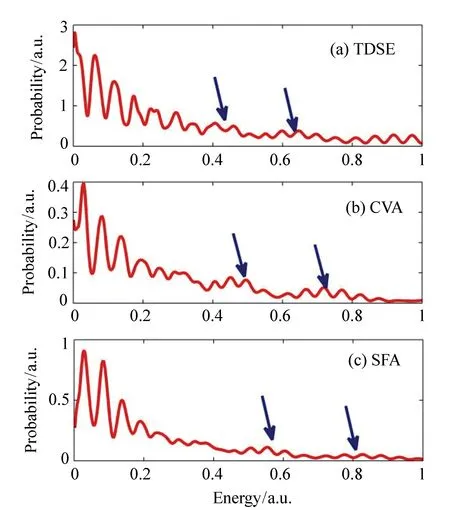
图5 H原子能量谱，激光参数与图1相同 Fig.5 Photoelectron energy spectra of H atom with under the same laser field as shown in Fig.1

图6(a)、6(c)及6(e)分别给出了氢原子在光学周期为2 cycles、4 cycles和8 cycles(对应的半峰全宽分别为1.9、3.8、7.6 fs)脉冲下的二维动量谱。 在2 cycles激光脉冲作用下得到的二维动量谱在pz<0的区域能看到明显的周期内干涉条纹，本文首次发现在pz>0的区域出现非常明显的径向条纹，使得该区域的周期内干涉条纹非常模糊； 4 cycles对应的动量谱中周期内干涉和周期间干涉均能明显观察到，除此之外，pz>0.5的区域出现了和图6(a) 类似的条纹，但是在周期内干涉作用下不是很清楚；在8 cycles脉冲作用下，pz>0.5区域的径向条纹仍然可以观察到。图6(c)及6(e)在00区域的图像是基本对称的，这与图6(a)有明显区别。为了分析库仑势对图6(a)、6(c)及6(e)中出现的径向条纹的作用，将作用势由长程库仑势换成短程势[19]，得到的二维动量谱如图6(b)、6(d)及6(f)所示。对比发现不考虑库仑势的情况下，动量谱在阈值附近的扇形条纹消失，变成了垂直条纹(预期的结果)，对上面所述径向条纹的出现并没有产生明显的影响。

图7采用SFA及CVA方法模拟了图6(a)的结果。模拟计算的电场如图7(a)所示，采用 SFA1、CVA得到的动量谱如图7(b)、7(c)所示，二者均未能重现出图6(a)的径向条纹，由于SFA1和CVA只涉及电子直接电离的情况，未考虑电子再散射。为了证实该条纹与电子再散射有关，本文在图7(a)中设置了两个时间窗对电子的电离时间tb以及返回母核发生再散射的时间tr进行了限制。根据经典的三步模型理论，在激光场峰值附近处电离的电子，会在激光场作用下大约经过0.75T左右的时间返回母核与电子发生再散射，因此将电离时间限制在-0.6T0方向运动，在激光场改变方向时返回母核附近与母核发生弹性散射，若发生背向散射将在pz>0区域被探测到。采用SFA2方法结合上述时间窗得到的动量谱如图7(d)所示，图中pz>0区域出现了明显的径向条纹，证明图6(a)中的径向条纹确实是再散射电子波包形成的；图7(e)为直接采用SFA2模拟的动量谱(不设置时间窗)，在pz>0区域出现了和图7(d)一致的条纹结构，再次说明了该条纹结构是再散射电子波包引起的，图7(d)在pz<0区域没有出现类似径向条纹，这是由于在2 cycles作用下其他峰值附近处电离的电子很难发生再散射。由于SFA2忽略了长程库仑势，所以在阈值附近的条纹成了垂直条纹。

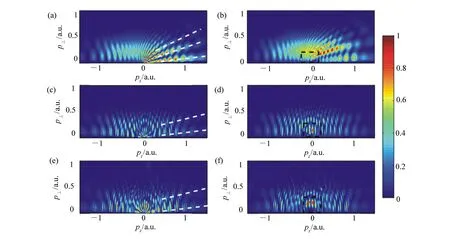
图6 H原子TDSE二维光电子动量谱，I=4.0×1014 W/cm2， λ=800 nm， CEP=0。(a)、(c)及(e)为考虑库仑势的计算结果，(b)、(d)及(f)为考虑短程势的计算结果；(a)和(b)脉冲持续时间为2 cycles；(c)和(d)为4 cycles；(e)和(f)为8 cycles Fig.6 TDSE 2D photoelectron momentum spectra of H atom when I=4.0×1014 W/cm2, λ=800 nm and CEP=0. (a)、(c) and (e) calculated with coulomb potential , (b)、(d) and (f) calculated without coulomb potential ; (a ) and (b) with 2 cycles pulse; (c) and (d) with 4 cycles pulse; (e) and (f) with 8 cycles pulse

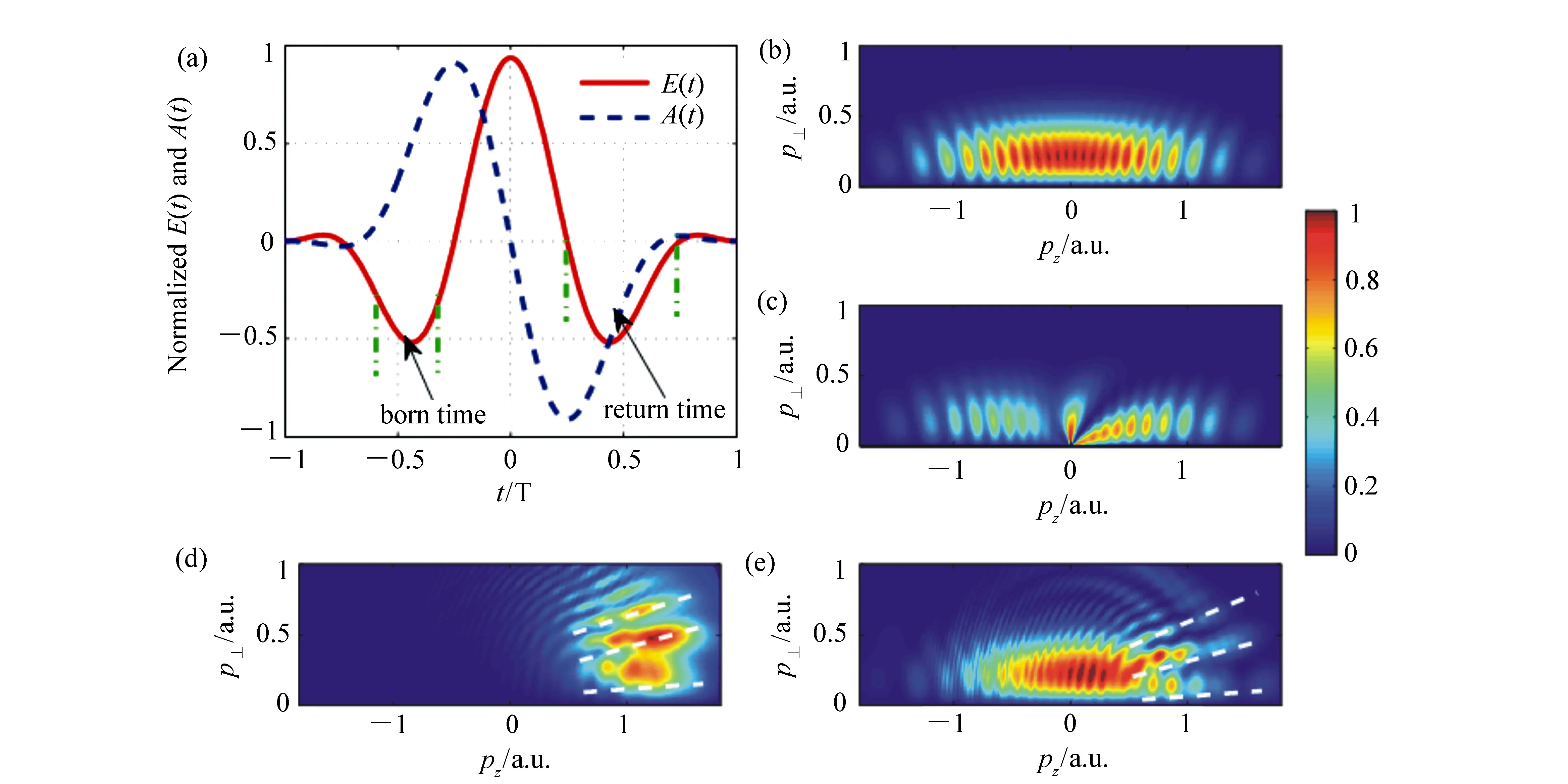
图7 H原子二维光电子动量谱及对应的电场和矢势，激光参数与图6(a)相同。 (a)电场和矢势 ；(b)SFA结果；(c)CVA结果；(d)SFA2结合时间窗的结果；(e)SFA2结果 Fig.7 Electric field and vector potential, and 2D photoelectron momentum spectra of H atom under the same laser field as shown in Fig. 6(a). (a)Electric field and vector potential; (b)result from SFA; (c)result from CVA; (d)result from SFA2 with time windows; (e)result from SFA2

4 结 论

本文采用SFA、CVA以及数值求解TDSE 3种方法研究了在深度隧穿电离机制下氢原子在线性极化少周期强激光场中的二维光电子动量谱。首先对比分析了SFA结合时间窗函数以及CVA结合时间窗函数模拟计算得到的氢原子电子波包周期内干涉及周期间干涉图像，发现长程库仑势作用下，周期内干涉条纹和周期间干涉条纹整体向阈值方向移动，在阈值附近受库仑势影响最为明显；更重要的发现是在库仑势作用下，周期内干涉和周期间干涉相互作用形成了二维动量谱中的扇形条纹。此外，利用TDSE方法求解了不同脉宽下的二维光电子动量谱，发现动量谱中除了周期内干涉条纹和周期间干涉条纹之外存在另外一种径向条纹结构，这些径向条纹在阈值附近受库仑势的影响明显，但是在pz>0.5的区域库仑势的影响几乎可以忽略，正是由于这种条纹的出现使得周期内干涉图像变得模糊。通过在SFA2模型中设置时间窗(电离时间以及返回时间)，重现了该结构，证实了该径向条纹是再散射电子波包干涉形成的，单独采用SFA2也模拟出了该结构。目前SFA模型中对再散射电子的贡献考虑不够，这是SFA模型急需改进的地方。