静止液态甲烷饱和单液滴蒸发模拟

邓佳佳, 许 健, 卢金树

(1.浙江海洋大学港航与交通运输工程学院,浙江舟山 316022; 2.浙江海洋大学船舶与机电工程学院,浙江舟山 316022)

天然气作为清洁能源受各界学者关注和研究[1-2],由于其产地与需求地不匹配,需长距离运输,长距离运输天然气最为经济的方法是采用LNG运输船运输[3]。为保证安全,LNG液舱投产前需预冷作业,使用制冷剂蒸气置换舱内气体,然后喷入雾化后的制冷剂液滴,通过相变吸热制冷[4],大型液舱一般采用LNG预冷[5-6]。Abramzon等[7]考虑多物性参数、Stenfan流及“吹拂效应”的影响,建立适用于喷雾燃料燃烧的近似蒸发模型。Haywood等[8]研究运动液滴在气流中蒸发,发现“吹拂效应”严重影响传质过程。Zhou等[9]考虑蒸发速率的影响,发现“吹拂效应”扰乱液滴蒸发过程中温度边界层的形成。前人研究主要基于组分梯度与扩散系数,而液舱预冷过程中制冷剂液滴在其蒸气中蒸发,无法描述组分梯度及扩散系数。目前,液体与其蒸气间的传热传质,通常采用Lee模型[10],Lee模型形式简单,适用于压力恒定且温度接近饱和温度、传热占据主导地位的过程,如管内水沸腾[11]和相变[12-13]。而LNG液舱预冷过程,初始环境温度远高于饱和温度,传质非常剧烈,高速蒸气喷出使边界层加厚,阻碍了传热过程[14],存在“吹拂效应”[9]。且液舱预冷过程中舱内温度变化大,“吹拂效应”的影响非恒定。这些因素Lee模型中均未考虑,因此不适用于LNG液舱预冷操作。故有必要建立适合液态甲烷液滴在其蒸气中蒸发的模型。笔者通过分析液滴蒸发过程,确立分步的研究思路,现阶段通过建立静止饱和单液滴在其蒸气中蒸发的模拟模型研究液态甲烷饱和单液滴在甲烷蒸气中的蒸发特性及“吹拂效应”的影响。

1 模型设计

基于能量守恒方程及质量守恒方程,建立静止饱和单液滴在其蒸气中蒸发模型。利用该模型对液态甲烷单液滴在甲烷蒸气中蒸发过程进行模拟。

1.1 假 设

静止液态甲烷饱和单液滴在其蒸气中蒸发过程非常复杂,为了简化模型,假设:①由于喷雾液滴粒径较小(最大为2.5 mm),可假设液滴保持球形,暂时忽略质量力对气相场的影响,可以将模型简化为球坐标系一维模型;②气液界面相变符合准稳态假设[7]且相变只发生在气液界面处;③液态甲烷液滴为饱和液滴且处于稳态蒸发阶段[15],液滴内部运动对传热传质的影响很小,暂时忽略液滴内部的运动带来的影响;④忽略热辐射带来的影响,只需计算液滴表面处的气相场区域。

1.2 物理模型

建立以静止液滴中心为球心,计算区域为液滴表面至距离球心0.5 m的球形物理模型,如图1所示。

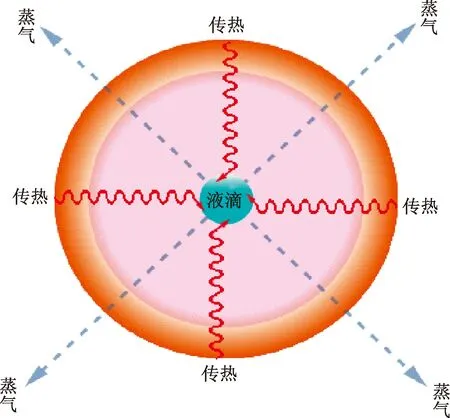
图1 液滴蒸发物理模型Fig.1 Physical model of droplet evaporation

1.3 数学模型

一维球坐标系下气相区域的能量方程[16]为

(1)

式中,ur为轴向蒸气速度,m/s;r为轴向位置坐标,m;cp为比定压热容,J/(kg·K);Γ为导热系数,W/(m·K);ρ为密度,kg/m3;T为温度,K。

根据界面处能量守恒(吸收的热量完全用于蒸发相变)以及质量守恒定律,得到液滴表面及其他区域的气相速度计算公式[17]为

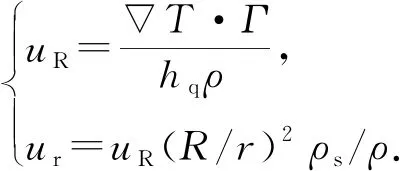
(2)

基于以上数学模型,对计算区域使用结构化网格进行划分,并对临近液滴附近网格进行加密处理。利用控制容积法对能量方程进行离散化处理,对流项采用二阶精度的中心差分格式。设置计算绝对残差收敛标准为10-10K,松弛因子为0.3,运用C语言编程,进行迭代计算求解,其中甲烷的导热系数通过状态方程[18]得到,计算程序流程见图2。

1.4 模型验证

由于液滴在同种蒸气中蒸发的相关研究国内外未见报道,因此对比模型计算和理论分析所得低温球(无蒸发)传热过程中温度边界层厚度(δT)并分析网格敏感度,以验证模型准确性。

低温球的传热公式[16]为

(3)

给定边界条件为

(4)

图2 程序流程Fig.2 Program flow

低温球δT表达式为

(5)

其中

式中,δT为温度边界层厚度,m;下标R,δ和∞分别为液滴表面、温度边界层处和无穷远处。

在温差为10～190 K工况下,对比模型计算与和理论分析所得半径为0.5和2.5 mm的液态甲烷低温球δT[17],对比结果如图3(a)所示,吻合较好。

对数量分别为100、1 000、2 000的粗、中、细网格进行液滴蒸发过程计算,采用累积均方根(RMS)[19]对比其差异, RMS的计算公式为

(6)

式中,ε1,2为累积均方根;N为样本数量;T1和T2分别为网格1和网格2计算温度,K。

不同网格温度对比见图3(b)所示,粗—中和中—细网格的RMS分别为1.48×10-2和5.44×10-6。可知,中等网格计算结果与细网格结果基本一致,但与粗网格结果差距较大,因此采用中等网格进行后续计算。

图3 模型验证Fig.3 Model validation

2 模拟结果与分析

采用所建模型,在半径R为0.5 ～ 2.5 mm,温差ΔT为10～190 K工况下,对静止液态甲烷饱和单液滴和低温球(无蒸发)在甲烷蒸气中的蒸发过程进行模拟,分析液滴蒸发特性以及“吹拂效应”的影响。

2.1 气液界面蒸气喷出速度

液滴为饱和单液滴,处于稳态蒸发阶段,吸收热量完全用于相变,并以蒸气的形式喷出。R及ΔT是气液界面蒸气喷出速度(uR)的重要影响因素。图4为气液界面蒸气喷出速度变化趋势。由图4可知,uR随R减小而增大,随ΔT增大而增大。进一步对uR、R以及ΔT之间的关系进行分析,发现uR与R乘积随ΔT呈现相同的变化规律,如图5所示。

牛顿冷却公式和uR表达式分别为

(7)

式中,A为液滴表面积,m2。

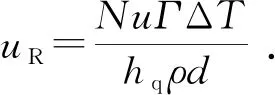
(8)

图4 气液界面蒸气喷出速度变化趋势Fig.4 Trend of uR

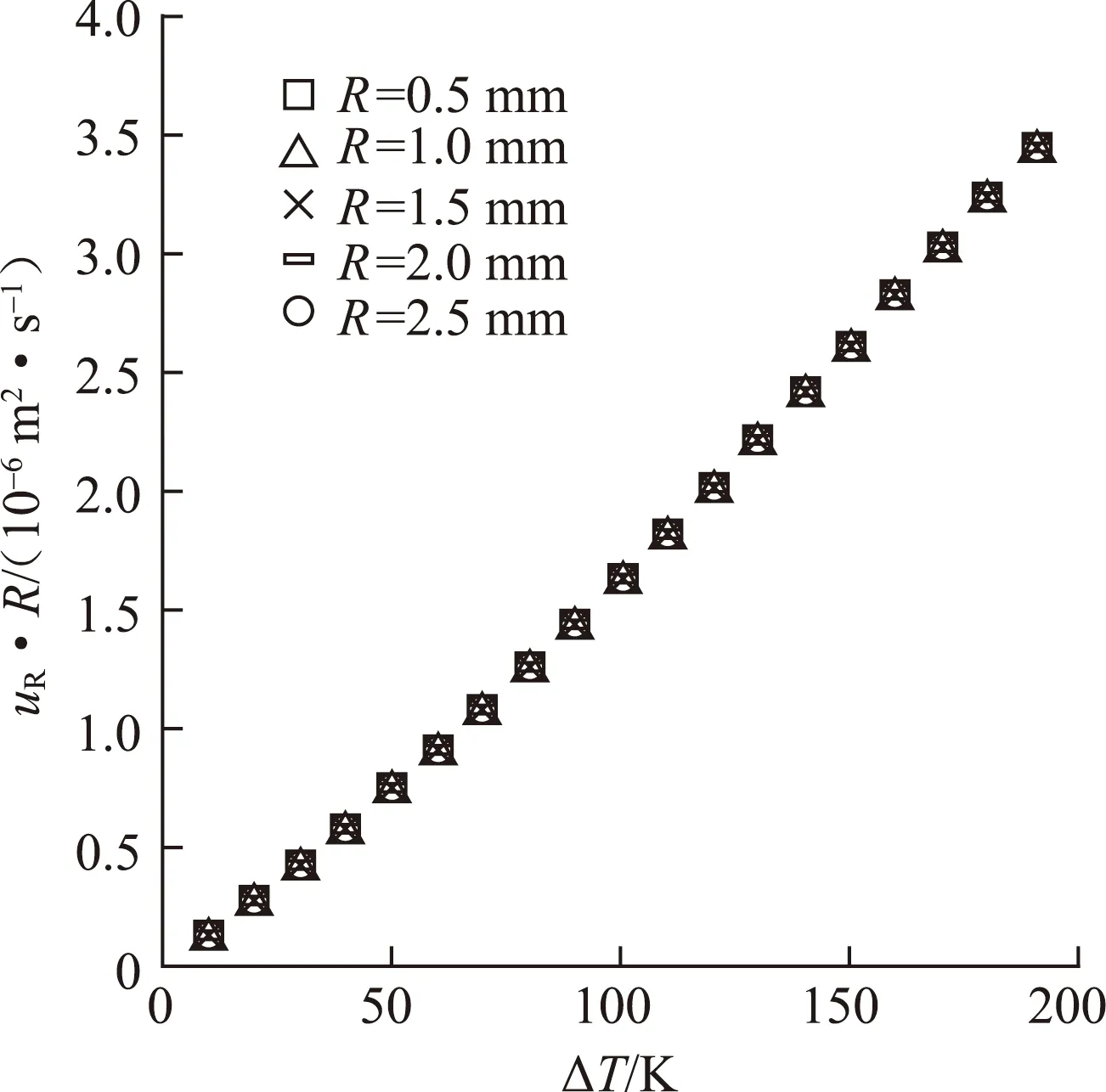
图5 气液界面蒸气喷出速度与温差、半径关系Fig.5 Relationship of R,ΔT and uR

由于静止液滴蒸发过程中Nu数一直以来被认为等于常数[9],uR又表示为

uR=KΔT/R.

(9)

式中,K为常数。

由公式(9)可以看出uR与R成反比,与ΔT成正比。

根据图5,对系数K进行计算,得出uR的计算式为

uR=1.69×10-8ΔT/R.

(10)

2.2 温度边界层厚度

液舱预冷过程中其初始环境温度远高于饱和温度,传质非常剧烈,高速蒸发蒸气喷出使δT加厚,阻碍了传热过程,这种现象称为“吹拂效应”。液态甲烷饱和单液滴在甲烷蒸气中蒸发,温度边界层厚度δT主要考虑R和ΔT及“吹拂效应”的影响。由于“吹拂效应”的影响暂无计算公式,将δT增厚率(α)定义为“吹拂效应”对δT的影响,计算式为

α=(δTd-δTc)/δTc.

(11)

图6为温度边界层厚度变化趋势。由图6可知:

(1)低温球δT随R增加而变厚,随ΔT增加而变薄。根据式(5)可知,低温球δT为R和J的乘积,J是仅与ΔT有关的无量纲系数。图7为系数J随ΔT变化趋势,随着ΔT加剧,J呈减小趋势。因此低温球δT随ΔT增大而变薄,随R增大而变厚。由于uR与传热方向相反,产生“吹拂效应”,造成相同工况下液滴δT比低温球厚。

图6 温度边界层厚度变化趋势Fig.6 Trend of δT

图7 系数J变化趋势Fig.7 Trend of coefficient J

(2)ΔT不变情况下,R越小,“吹拂效应”越明显。在ΔT=190 K工况下,“吹拂效应”使R=0.5 mm液滴δT增长28.8%,使R=2.5 mm液滴δT增长22.03%。R不变情况下,ΔT越大,“吹拂效应”对δT影响越剧烈。R=2.5 mm工况下,ΔT=10 K时,“吹拂效应”使δT增加1.06%;ΔT=190 K时,“吹拂效应”使δT增加22.03%。

2.3 热流密度

δT变厚,将导致传热受阻,造成热流密度(q)减少。热流密度计算式为

q=hqρsuR.

(12)

将q减少率(β)定义为“吹拂效应”对q影响,计算式为

β=(qc-qd)/qc.

(13)

式中,β为“吹拂效应”对q的影响率;q为热流密度,W/m2。

本文提出了一种基于二元域等效的RS码识别方法，能有效完成码长、信息分组长度和生成多项式的识别.方法遍历本原多项式，并随之构建二元域分析矩阵和校验向量对其进行检验.为了提升识别性能，先后进行两次判决，进而确定本原多项式、码长和信息分组长度.最后，利用连续根分布计算生成多项式.该方法性能优良、计算量低，易于工程实现.后续研究将主要针对缩短RS码，以进一步完善方法的适用范围.

图8为热流密度变化趋势。由图8可知,液滴q随ΔT增大而增大,随R增大而减小,这与uR的变化特性一致。由于“吹拂效应”影响,传热受阻,相同工况下,液滴q相对于低温球较小。“吹拂效应”对q影响仅与ΔT有关,温差由0提高到190 K,“吹拂效应”的影响由0线性增加至27.7%。

图8 热流密度变化趋势Fig.8 Trend of heat flux

2.4 质量蒸发率

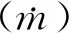
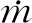
(14)

(15)

图9 蒸发速率对比Fig.9 Trend of evaporation rate

图10 温差、半径、蒸发速度关系Fig.10 Relationship between ΔT,R and

3 结 论

(1)液滴蒸发过程中气液界面蒸气喷出速度与半径成反比,与温差成正比。

(2)低温球温度边界层厚度随着半径增加而变厚,随温差增加而变薄;在“吹拂效应”影响下,液滴温度边界层比相同工况下要厚,半径越小温差越大,“吹拂效应”影响越剧烈。温差为190 K、半径为0.5 mm工况下,“吹拂效应”对温度边界层厚度影响最剧烈,使温度边界层厚度增加28.8%。

(3)“吹拂效应”阻碍传热过程,使热流密度减少;“吹拂效应”对热流密度的影响仅与温差有关,温差由0增大至190 K,热流密度减小率线性增加至27.7%。