多层局部感知卷积神经网络的高光谱图像分类

池 涛 ， 王 洋， 陈 明

(1.上海海洋大学 农业部渔业信息重点实验室， 上海 201306;2. 喀什大学计算机科学技术学院， 喀什 944104)

1 引 言

高光谱影像HSI(hyperspectral image)[1]含有丰富的光谱信息和空间信息在空间观测和目标识别中有着重要地位. 它广泛使用在现代军事、精准农业以及环境监控等诸多领域.

高光谱图像分类[2]是高光谱影像处理和应用的重要组成部分. 高光谱图像包含了上百个光谱通道，并且具有高维特性、波段间高度相关性以及光谱混合等特性. 这使得高光谱图像分类成为一个巨大的挑战. 由于光谱信号的高维度、不确定性、信息冗余以及表面覆盖的异构性和同质性，使得高光谱数据结构具有高度非线性的特征，这导致基于统计模式识别的分类模型难以直接分类和识别高光谱数据. 同时，样本数量有限并且质量好坏不一，从而导致分类器模型的参数难以估计或者估计不准确. 在这些情况下，高光谱图像的准确分类需要建立复杂的数学模型，从而可以真实的反映数据的内在本质. 模型训练过程需要繁琐的预处理和后处理. 通过研究和实践表明，传统的遥感影像技术在分析高光谱图像时无法解决高维数据小样本识别、高光谱图像分类精度等问题，目前机器学习、计算机视觉以及模式识别的理论和方法成为高光谱图像分类的重要技术手段.

为了实现高效、高精度的高光谱图像分类，曾在高光谱图像上采用K邻近算法、主成分分析(principal components analysis, PCA)、支持向量机SVM(support vector machine)等方法. 随着特征提取和分类方法改进，提出了光谱空间分类法、局部Fisher判别法、U-Net卷积神经网络分割图像法[2]等多种方法，取得了较好的结果. 其中，支持向量机SVM[3]被认为是高效和鲁棒性良好的方法，适用于小规模训练样本. 它是一种监督学习模型，通过非线性映射将样本空间映射到一个高维甚至无穷维的特征空间(Hilbert空间)中. 将原始样本空间中的非线性可分问题变成比原始样本空间更高维度空间中的线性可分问题，并在高光谱图像分类中有着良好的效率和正确率.

以卷积神经网络CNN(convolutional neural network)[4]为代表的深度学习技术在图像分类和模式识别方面具有良好的性能. 随着神经网络的发展，CNN越来越多的被应用于高光谱数据的分类. 例如，多层感知器MLP(multilayer perception)[5]和径向基函数RBF(radial basis function)[6]的应用.

CNN方法在机器视觉方面分类效果优于传统的SVM分类器. 实际上，在高光谱图像分类任务中，SVM在分类精度、时间复杂度和空间复杂度方面优于传统的神经网络的，但不能因此放弃神经网络这样强大的工具. 在本文实验过程中，当训练数据足够大时，本文提出的改进型卷积神经网络的精度可以优于SVM.

文献[7]提出的卷积神经网络网络，只有Alexnet网络参数的10%大小，在计算机视觉上的分类精度和算法效率上优于Alexnet网络. 文献[1]中将CNN直接应用于高光谱分类中，本文通过实现该论文中方法作为改进前CNN网络. 本文通过文献[7]中提高卷积神经网络的非线性特征学习能力的改进策略应用对高光谱影像分类的CNN方法改进，改进后的网络结构能够有效提高对高光谱影像非线性特征的学习能力，有效提高分类精度[7].

2 多层局部感知卷积神经网络

针对高光谱图像每个像素的不同频谱的特征具有非线性，本文提出在传统CNN网络的基础上通过改变卷积层感知器和激活函数，并且引入批标准化层，实现多层局部感知网络结构，增强其对非线性特征的学习能力.

2.1 增强非线性特征学习的改进方法

2.1.1 多层感知器卷积层(Mlpconv layer) 经典卷积神经网络中的卷积层实际使用线性滤波器对图像进行内积运算，与单层神经网络类似，卷积滤波器实际就是一种广义线性模型GLM(generalize linear model)， GLM的抽象能力相对较低. 例如Lenet-5[8]是一个经典的卷积神经网络结构，它的卷积层为线性滤波器.

线性卷积层假设其上层一个输入为xm，步长为s，卷积核大小为k，激活函数为f，输出为n(指代由一个样本数据通过n个神经元输出n个数据，在这里没有给定具体数值仅仅代表这个变量与图1中下标n对应，以更好描述一个线性卷积层结构和运算过程，在2.2节中给出模型的具体数值)，i代表0～n之间的第i个输出数据或第i个神经元；j代表输出数据中第j个基本数据；神经元激活函数为f；权重矩阵W；偏置为b(每个神经元由激活函数、权重矩阵和偏置三部分组成)；T为转置，该卷积层的过程如图1所示.

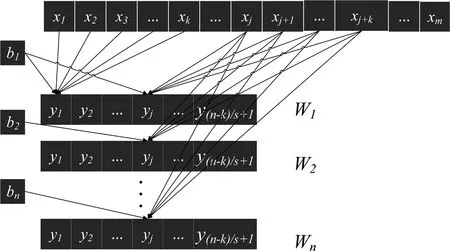
图1 线性卷积层Fig.1 Linear convolution layer

则线性卷积层中第i个神经元的计算公式如下.

(1)

本文对卷积神经网络的卷积层进行了较大的改进，使用MLP(多层感知器)作为卷积层模型，从而提高非线性特征学习能力. 在实际使用过程中，通过在经典卷积层后增加两层卷积核为1*1的卷积层实现. 由于采用了Mlpconv卷积层，网络在前面卷积阶段特征提取效果提高，极大地减少了参数和过拟合风险.

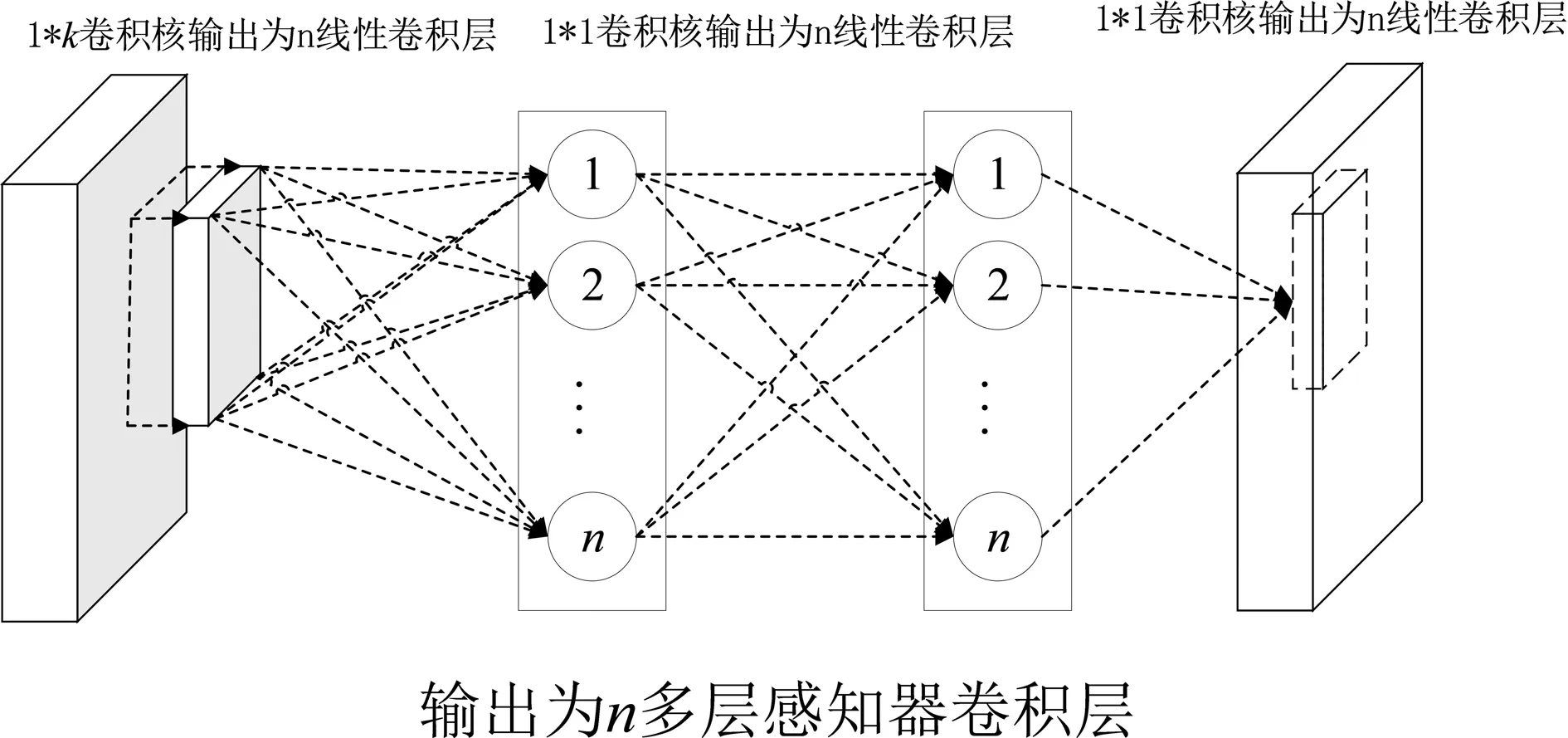
图2 多层感知器卷积层Fig.2 Mlpconv layer

从图2可以看到，Mlpconv卷积层网络结构就是在图1的基础上增加两层卷积核为1*1，输出为n，步长为1，相同激活函数的卷积层. 简而言之，多层感知器卷积层使用Mlp网络结构，对局部感受野的神经元进行更复杂的运算操作，可以对非线性特征更加敏感，而线性卷积层，局部感受野的运算仅仅只是一个单层的神经网络.

2.1.2 激活函数层(activation function layer)所谓激活函数(activation function)，就是在人工神经网络的神经元上运行的函数，负责将神经元的输入映射到输出端. 通过在激活函数给神经元引入了非线性因素，从而使得神经网络可以更加逼近任何非线性函数，这样的神经网络就可以被应用于更多的非线性模型中.

常用的Relu激活函数(the rectified linear unit)，被使用于隐藏层神经元输出. 与线性激活函数相比，Relu激活函数克服了梯度消失、训练速度等问题，但在实验过程中，大量局部神经元出现饱和情况(也称神经元死亡)，无法有效学习特征. 因而本文方法采取Relu激活函数(the rectified linear unit)的变种，带泄露线性整流(Leaky ReLU)[9]. 当输入x为负时，带泄露线性整流函数(Leaky ReLU)的梯度为一个常数λ∈(0，1)，而不是0. 当输入为正时，带泄露线性整流函数和Relu激活函数保持一致. 数学表达方式：

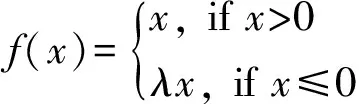
(2)

本文使用MATLAB神经网络工具箱函数提供的默认值0.01作为常数λ的取值，同时参考多数神经网络模型取较小的数值作为常数λ的取值就可以避免饱和现象. 通过实验测试，当常数λ∈(0.005，0.1)时既可以避免饱和现象，同时加速模型收敛. 当取值过大训练时间增加，当取值过小则无法避免饱和现象影响正确率.

2.1.3 批标准化层(batch normalization) 本文在每个卷积层中激活函数层之前增加批标准化层(batch normalization)[10]，实际过程表现为对卷积层的神经元批量标准化处理，对于在非线性函数映射后不断向取值区间饱和区靠拢的输入分布强行映射到比较标准的正态分布，使非线性变换函数的输入落入对输入值比较敏感的取值区间，从而解决梯度消失问题. 设同一最小批次B有m个样本：B={x1...m}；神经元激活函数为f;权重矩阵W; 偏置为b; 左箭头符号为命题的“条件”运算，一般可以根据实际数据再做调整，在本文中该符号与等号含义相同. 本文通过实验测试最小批次样本数为96个，可以使多数样本数值调整到合理区间范围内，能有效提取特征，提高训练模型分类精度.

最小批次B均值如下式.

(3)

最小批次B方差如下式.

(4)

标准化处理如下式.

(5)

卷积激活如下式

(6)

传统线性卷积层中神经元做卷积和激活操作，改进后卷积层对同一神经元同一批次做批标准化处理、然后在标准化后的样本上进行卷积和激活操作. 本文将批标准化层(batch normalization)引入卷积层中，可以增加训练速度，加快收敛过程，减小局部神经元死亡风险.

2.2 多层局部感知卷积神经网络分类器

2.2.1 多层局部感知CNN网络模型 卷积神经网络是一种人工神经网络. 它实际上是一种前馈式神经网络，一般包含卷积层(convolutional layers)、池化层(pooling layers)和全连接层(fully connect layers). 每个隐藏层神经元通过连接输入的一部分并非全连接，通过利用过滤器的局部敏感性实现模型对于目标不同空间域的相关性的学习. 经典的卷积神经网络结构为LeNet-5，每个隐藏层连接一部分输入图像区域. 该网络结构受猫的脑部视觉皮层工作原理启发，通过模拟视觉皮层细胞对局部的视野非常敏感，敏感区域也是感受野，大量的感受野感受整个视野，同时这也会造成神经元过多，参数过大问题，这些感受野通过共享权重的方式解决该问题. 对于大多数二维图像识别的卷积神经网络结构，输入层之后是由卷积层和最大池化层交替叠加构成，接近输出层由全连接层构成. 典型的卷积网络结构如图3所示.

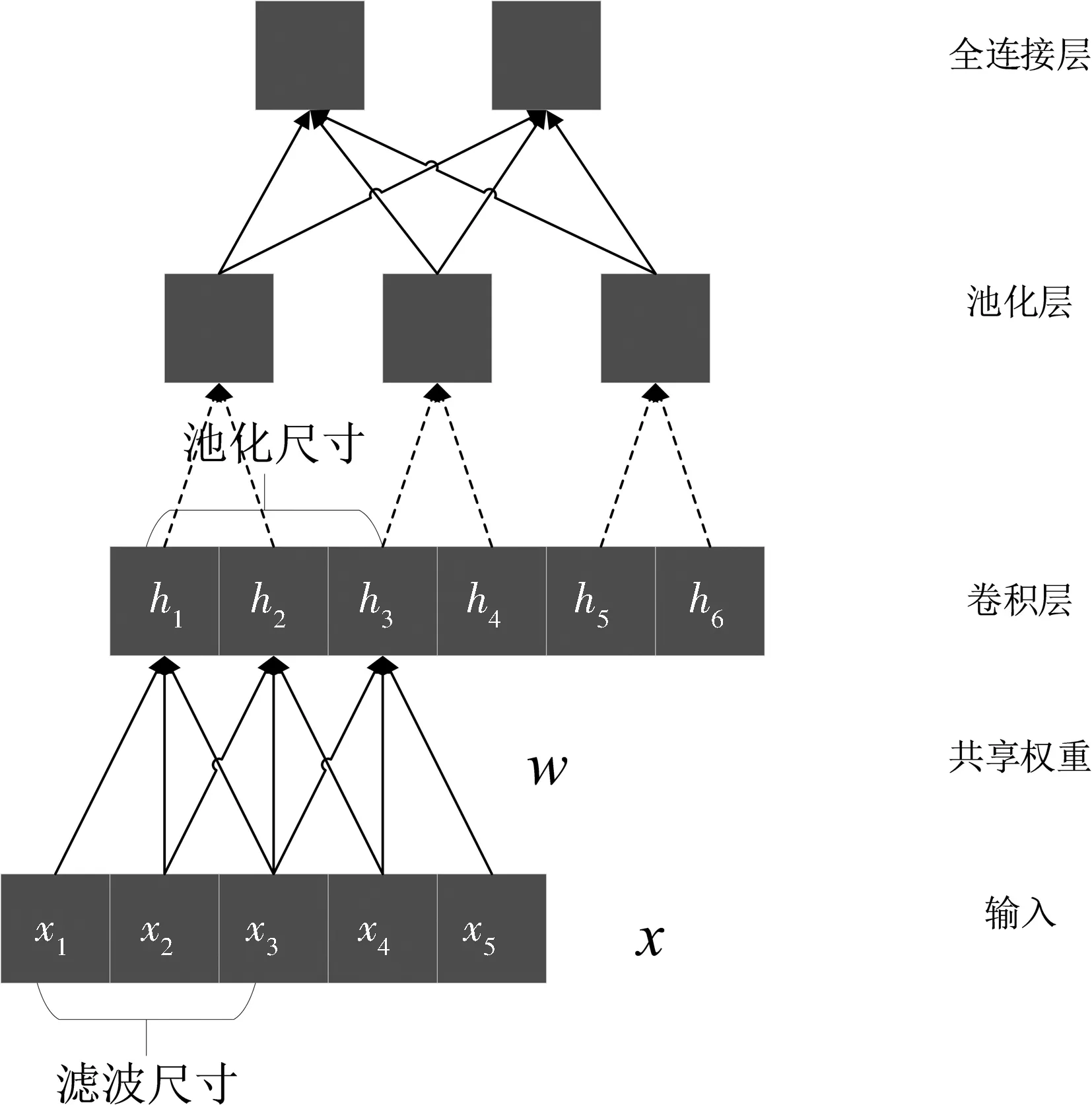
图3 典型的卷积神经网络结构

在卷积神经网络中用多层感知器卷积层(Mlpconv Layer)代替线性卷积层(linear convolution layer)提高卷积神经网络对于非线性特征的学习能力. 改进后卷积神经网络结构如图4所示.

图4 改进后卷积神经网络结构Fig.4 Improved convolutional neural network structure

2.2.2 构建增强非线性学习的CNN分类器 本文构建的卷积神经网络结构如图5，其中共包含7层，分别是输入层、卷积层C1、卷积层C2、卷积层C3、最大池化层M4、全连接层FC5、输出层. 设输入尺寸为1*m1*1，其他各层输出尺寸1*m2*1、1*m3*1、1*m4*1、1*m5*1、m6、m7.

图5 多层局部感知CNN分类器Fig.5 Multi-layer local perceptual CNN classifier

高光谱图像中的每一个像素样本是一个三维矩阵，该矩阵的列数为1，行数m1为高光谱图像频谱的个数(以Pavia University数据为例，该数据集频谱个数为115，但采用良好的103个频段，所以行数为103)，该数据同时是单通道所以通道数为1. 这样构造方式将一个像素点作为一张图片识别. 因此输入层为(1*m1*1)，m1为频谱的个数. 卷积层C1是n个大小为(1*k)的卷积核构成. 因此，该卷积层输出1*m2*1*n. 最后输出层n’，由识别物体种类决定;详细网络结构及计算过程如表1和式(7)所示.

表1 多层局部感知CNN分类器

以下是各层尺寸计算公式.

(7)

2.3 基于像素分类策略

本文提出的多层局部感知卷积神经网络结构有利于高效并且准确地提取非线性特征. 但对于高光谱图像分类，面临另一个主要问题是如何建模和调整输入层的数据格式.

在图6～图8中所展示的光谱信息，将Pavia University数据中每个像素点所包含的所有光谱通道融合成一条曲线反应在二维坐标值上. 横坐标表示103个谱段，纵坐标代表每一个像素点该波段的幅值. 在图6～图8中很难直观上判别不同地物的频谱特征差别，但可以观察到每一种地物的光谱曲线明显不同于其他地物的光谱曲线.

图6 沥青道路像素的光谱信息Fig.6 Spectral information of asphalt road pixels

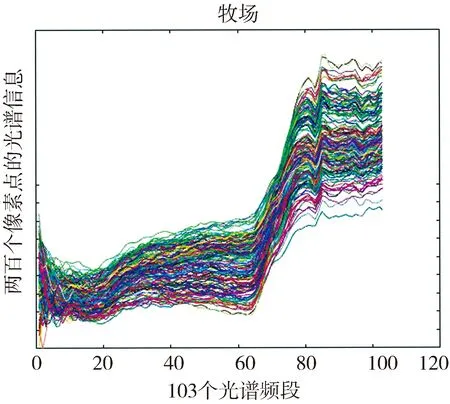
图7 牧场像素的光谱信息Fig.7 Spectral information of pasture pixels

本文对高光谱图像数据的分类处理方式为硬分类[11]，将高光谱图像中每个像素都赋予单个类别，划分方式只要是通过像素的光谱特征和已知每个类别光谱特征的相似性来区分.

基于像素分类策略，通过各种方法分析和提取不同目标物之间光谱域特征，调整数据输入格式，对不同方法进行测试.

以Pavia University数据集为例，对于该图像640*340中的每个像素的103个谱段上的幅值组成1*103*1的矩阵作为输入. 这种提取像素的方式，不考虑像素间的空间关系，仅仅通过每个像素在不同谱段的光谱信息特征提取用于分类.

2.4 基于改进CNN的分类及训练过程

2.4.1 正向传播 多层局部感知卷积网络结构包含7层，输入单元n1构成输入层，输出单元n7构成输出层，此外隐藏单元包含卷积层C1、卷积层C2、卷积层C3、最大池化层M4和全连接层FC5. 设第i层的输入为xi，也是第(i-1)层的输出，数学表示如下式.

(8)

式(8)中，W是第i层的权重矩阵，对输入进行权重相乘；b为第i层的偏置矩阵；f为第i层的激活函数. 卷积层C1、卷积层C2、卷积层C3和全连接层FC5适用.

2.4.2 动量梯度下降方式反向传播误差更新权重 本文使用梯度下降算法反向传播误差进行权重和偏置的更新. 首先我们先定义一个代价函数(误差定义)，如下.

(9)

式中，C被称为二次代价函数，也称均分误差或者MSE；m为训练数据集的个数；a:目标值(对应输入x).

综上，训练卷积神经网络的最终目标是求出最小化二次代价函数C(w，b)的权重和偏置梯度下降算法对权重和偏置进行训练使得代价函数最小化. 简化的更新公式如下所示.

(10)

式中，右箭头符号为命题的“条件”运算；η为学习率.

同过迭代上述更新权重和偏置的公式，对每一 个输入和目标不断训练参数，从而使得最终代价函数最小化. 一般学习率设置在0.01左右，学习率过大或者过小都会使得模型无法达到预想的精度，当加入batch normalization层后，可以增大学习率对精度影响变小，本文通过实验测试，将学习率调整为0.035.

为进一步提高本文方法分类精度，引入加入动量的梯度下降算法，从而进一步提高训练出模型的精度. 改进后的更新公式如下.

(11)

式中，t为更新的次数，公式指代当前更新的权重和偏置；γ为动量，为考虑上次更新的权重、偏置与这次权重、偏置之间的因素对更新权重、偏置的影响. 增加动量这个常数. 本文采用默认值0.9，通过增加动量优化后，进一步提高了训练模型的分类精度.

3 实 验

本文算法在MATLAB2018b上运行，PC机配置Intel(R)Core(TM)2 Duo CPU E7500，2.93 GHz处理器，ATI Radeon HD 3400 Series显卡.

3.1 数据集

本文实验选用的常用的高光谱数据集为Pavia University数据和Salinas数据集[12]. 通过这种小训练样本的方式，检测该方法是否能够提取不同目标物像素点光谱域的有效特征. 在输入前数据做z-score标准化，提高其他算法的计算速度和精度，同时加快神经网络梯度训练时候的收敛速度.

3.1.1 Pavia University数据 Pavia University数据是由德国的机载反射光学光谱成像仪(reflective optics spectrographic imaging system，ROSIS-03)对帕维亚大学所拍摄的一部分高光谱数据. 其中,光谱成像仪在0.43～0.86 μm 波长范围内的115个波段连续成像，空间分辨率为1.3 m. 其中剔除了12个受噪声影响的波段，因此采用剩余103个光谱波段所呈的图像. 该图像的尺寸为 610×340，包含207 400个像素，但是其中包含164 624个背景像素，因而只有 42 776个包含地物的像素，这些像素中共有9类地物，包括树(tree)、沥青道路(asphalt)、牧场(meadows)、彩绘金属板(painted metal sheets)等，详细数据信息见表2.

表2 Pavia University高光谱数据集

3.1.2 Salinas数据 Salinas数据是由 AVIRIS成像光谱仪所拍摄的美国加利福尼亚州的 Salinas山谷图像. 该图像的空间分辨率为3.7 m. 该图像原本有 224个波段，因为噪声剔除了第108～112，154～167，还有不能被水反射的第224个波段后剩下的204个波段的图像. 该图像的尺寸为512×217，因此包含 111 104个像素，其中包含56 975个背景像素，可用于分类的像素有54 129个，这些像素总共分为 16类，包括休耕地(Fallow)、芹菜(Celery)等，详细数据见表3.

3.2 实验结果与分析

本文为测试各个模型的时间与空间复杂度、过拟合程度和精度三个方面，从而设计了以下实验.

(1) 实验中所用到的训练集的选择方式如下.

训练集1 在每一类目标物当中随机挑选400个像素点作为训练集.

训练集2 在每一类目标物当中随机挑选一半像素作为训练集.

(2) 实验中所用到的测试集的选择方式如下.

测试集1 在训练集1随机挑选完后剩余像素中的每一类目标物当中随机挑选200个像素点作为测试集.

测试集2 所有目标物像素点作为测试集.

本文提出的多层感知卷积神经网络、改进前原型和Linear-SVM三种方法形成对比，本文方法与改进前原型的卷积核大小、参数设置、训练方法、训练批次、批次大小等方面完全一致. Linear-SVM和其他方法未进行参数优化. Linear-SVM和RBF-SVM使用的是MATLAB中统计和机器学习工具箱实现.

卷积神经网络都采用动量梯度下降算法，图9展示本文方法在训练集1上的训练过程，其中包含正确率和损失率.

表3 Salinas高光谱数据集

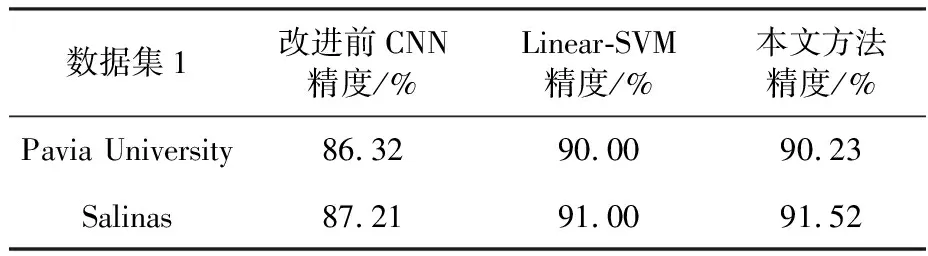
表4表明,在小样本分类中，本文方法相对于改进前CNN在精度上有着明显提高，同时略微优于传统高光谱分类的Linear-SVM方法. 测试结果说明，在小规模训练样本情况下，本文改进策略有效提高了卷积神经网络高光谱分类的精度. 同时说明本文改进策略提高了模型对非线性特征的提取能力.

表4不同数据集的三种算法对比结果测试结果(训练集1和测试集1)

Tab.4Threealgorithmcomparisonresultstestresultsofdifferentdatasets

数据集1改进前CNN精度/%Linear-SVM精度/%本文方法精度/%Pavia University86.3290.0090.23Salinas87.2191.0091.52

图9 本文方法训练过程Fig.9 Method training process

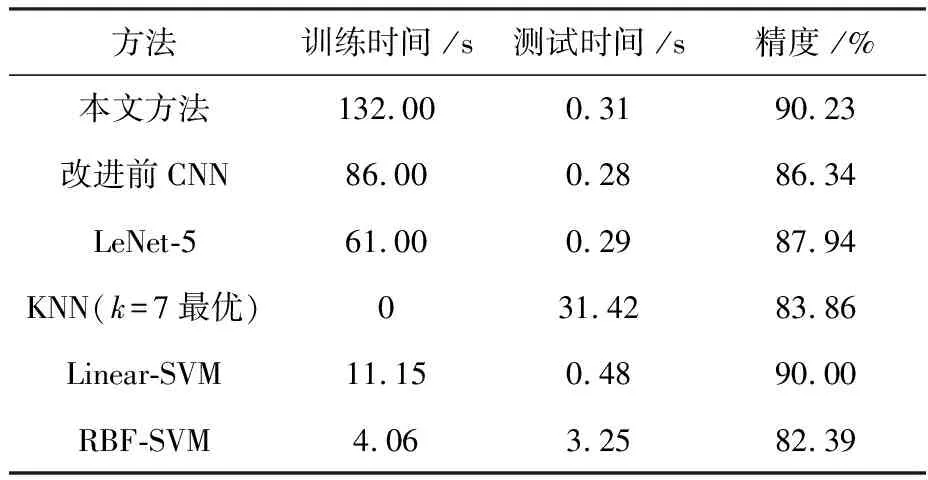
表5对于训练集1和测试集1各个方法的性能对比(PaviaUniversity数据集)

Tab.5Performancecomparisonofeachmethodoftrainingset1andtestset1

方法训练时间 /s测试时间 /s精度 /%本文方法132.000.3190.23改进前CNN86.000.2886.34LeNet-561.000.2987.94KNN(k=7最优)031.4283.86Linear-SVM11.150.4890.00RBF-SVM4.063.2582.39

在表5中，本文方法相对于改进前CNN训练时间增加，有更多的网络参数需要计算. 在仅增加0.03 s情况下提高了模型的分类精度. 同时在分类时间几乎相等情况下，在精度上击败了经典的卷积神经网络结构LeNet-5. 相对于传统的SVM在小样本分类中不仅分类速度上和分类精度上都有明显改进.

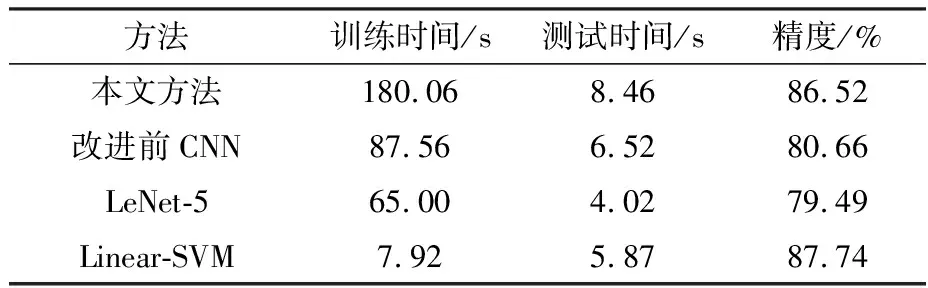
表6对于训练集1和测试集2各个方法的性能对比(PaviaUniversity数据集)

Tab.6Performancecomparisonofeachmethodoftrainingset1andtestset2

方法训练时间/s测试时间/s精度/%本文方法180.068.4686.52改进前CNN87.566.5280.66LeNet-565.004.0279.49Linear-SVM7.925.8787.74

将测试集1替换成测试集2得出的表6实验结果. 在表6中，所有模型的分类精度都有下降，出现不同程度过拟合现象. 本文方法，随着测试集增大，测试时间相对于其他模型增长稍大，实际使用过程中依然可以接受. 传统SVM依然能保持良好高效的性能.

表7量化过拟合现象，过拟合程度数值由第二列减第三列的差值然后与第三列的比值得出. 在小样本训练集情况下，传统SVM能有效提取数据特征，本文方法相对于其他传统卷积神经网络大大减小了过拟合程度，多层局部感知结构能有效提高对非线性特征的提取能力.

表7 对于训练集1各个方法的过拟合程度

表8对于训练集2和测试集2各个方法的性能对比(PaviaUniversity数据集)

Tab.8Performancecomparisonofeachmethodoftrainingset2andtestset2

训练2测试得到表8实验结果，通过增大训练集卷积神经网络可以达到更高的分类精度，多层局部感知神经网络相对于其他神经网络在高光谱图像分类上有着更高的精度，有着更好的非线性特征提取能力. SVM依然有着高效性能和分类精度，但无法提取更多的特征.

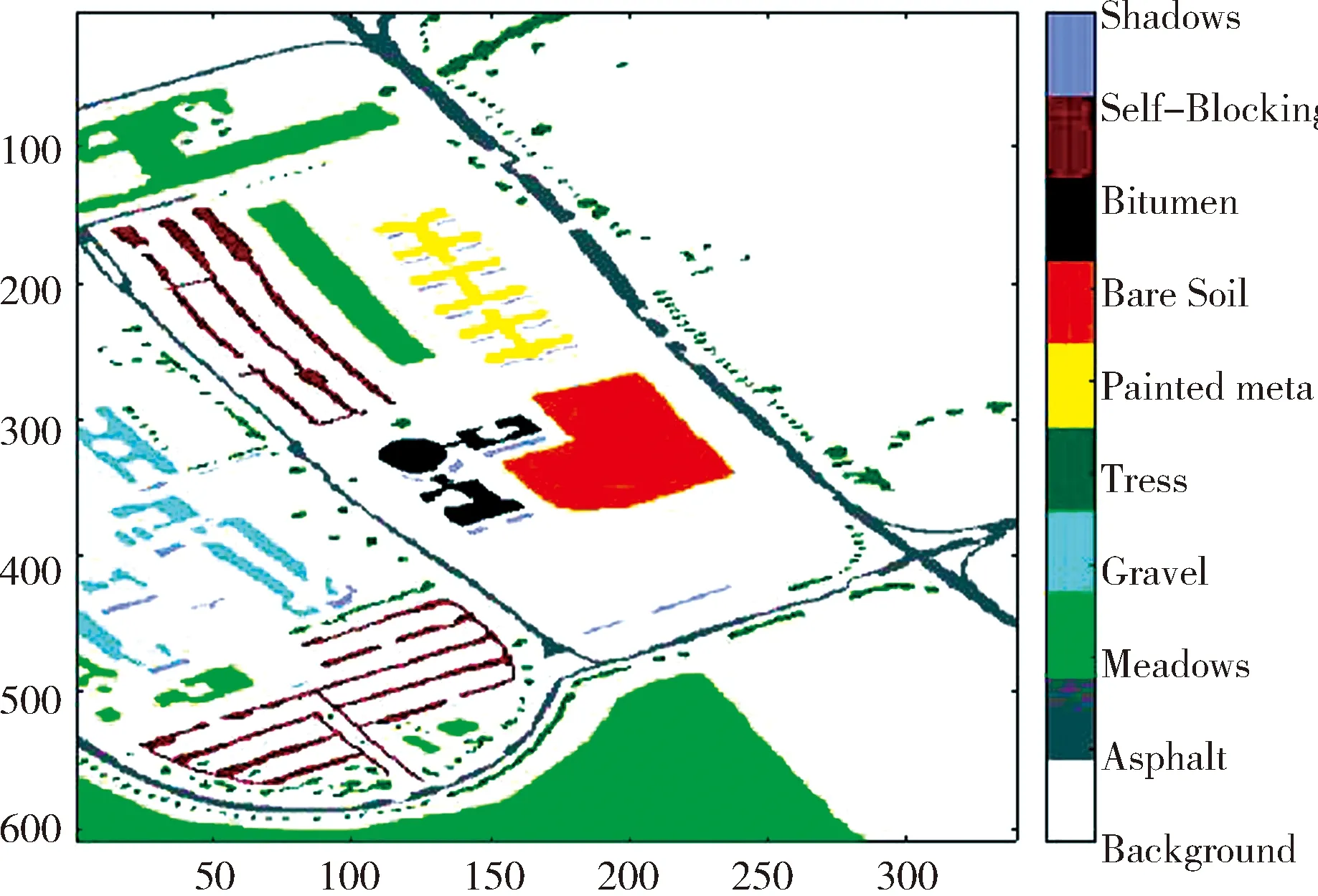
图10 Pavia University数据集目标可视化Fig.10 Pavia University dataset target visualization

综合上述实验结果说明，SVM在小规模训练样本上的计算成本和训练时间都是有着较高优势，但是随着训练集增大，精度无法做到最优，并且需要参数优化，才能达到较好的精度. 改进前CNN方法和LeNet-5在小规模训练样本上，不能达到良好的分类精度. 在较大规模训练样本情况下，神经网络有着更高的分类精度. 随着训练集增大，可以学习到更多的有效特征. 本文提出多层局部感知神经网络能更加有效提取样本光谱特征，同时也随着训练集增大，精度能有效提高. 相比传统的LeNet-5深度学习网络和SVM，本文提出的方法无论在小样本分类和大样本分类都能有效提取特征，相对于改进前的CNN分类器和LeNet-5在精度上有着明显提升[13].

图11～图13展示各种方法在训练集2训练下的测试集2的测试可视化结果.

图11 Linear-SVM预测结果92.40%精确度

Fig.11 Linear-SVM prediction results 92.40% accuracy

图12 LeNet-5预测结果96.64%精确度Fig.12 LeNet-5 forecast results 96.64% accuracy

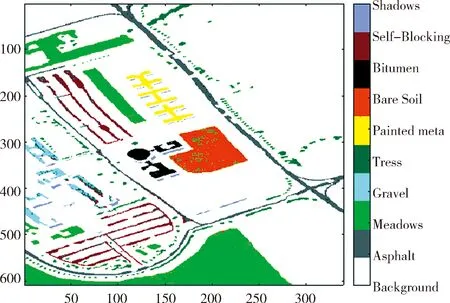
图13 本文方法预测结果97.23%精确度Fig.13 This method predicts 97.23% accuracy

4 结 论

本文在Pavia University数据和Salinas数据集上进行多种方法测试，SVM在小样本训练中有着有效提取特征的能力，本文通过对传统卷积神经网络进行改进确实有效提高了在小样本和大样本训练时的非线性特征学习能力，都达到最佳的精度. 在较大规模训练样本时，卷积神经网络有着良好的进一步学习能力. LeNet-5网络结构在大训练样本时表现出高效的分类精度，表明深度学习网络在高光谱图像分类上有着良好的潜力[14].

下一步，将U-net网络和NIN网络结构应用于高光谱分类中，进一步提高分类精度同时避免过拟合，在考虑新的分类策略，通过软分类方式考虑像素空间域和光谱域相关性特征，更进一步提高分类精度[15].