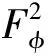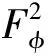广义Fock空间之间的Volterra型积分算子与复合算子的乘积
罗小娟, 王晓峰, 夏 锦
(广州大学数学与信息科学学院,广州 510006)
1 Introduction
LetCbe the complex plane andφ:[0,∞)→R+a twice continuously differentiable function. We extendφtoCby settingφ(z)=φ(|z|),z∈Csuch that
cω0≤ddcφ≤Cω0
(1)

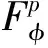

Note that we will writeABfor two quantitiesAandBif there exists an unimportant constantCsuch thatA≤CB. Furthermore,BAis defined similarly and we will writeA≈BifABandBA.
Forz∈Candr>0, letD(z,r)={w∈C:|w-z| |Kφ(z,w)|e-φ(z)e-φ(w)≤Me-θ|z-w|≤M (2) and, in addition, there exists positive constantr0such that |Kφ(z,w)|e-φ(z)e-φ(w)≥MKφ(z,z)e-2φ(z)≥M (3) forz∈Candw∈D(z,r0). With above results, we have Kφ(z,z)≈e2φ(z),z∈C (4) IfHis a holomorphic function space onC, we can define the Volterra type integral operator onHinduced by a holomorphic symbolgas Pommerenke[2]characterizes the boundedness, compactness, and other operator theoretic properties ofVgin terms of function theoretic conditions ongin 1977. There are a lot of interest following works about operatorVg, for instance, Alemanetal[3-4]on Hardy and Bergmann spaces. For more information, we refer to Refs.[5-7] and the references therein. The Volterra type integral operatorVghas an essential relationship with the multiplication operatorMg(f)=gfby Mg(f)=f(0)g(0)+Vg(f)+Ig(f), whereIgis the Volterra companion integral operator given by Letψbe an entire function andCψf=f(ψ) be the composition operator on the space of analytic functions onCwith symbolψ. The induced product of Volterra type integral and composition operators is defined by In this paper, we obtain some equivalent characterizations for the boundedness, compactness, and Schatten-pclass properties of the product of Volterra type integral and composition operators between generalized Fock spaces in terms of certain Berezin transforms on the complex planeC. By modifying all the results stated forV(g,ψ), one could also obtain similar results for the Volterra type composition operators For 0 thep-distortionfunction ofφis defined by Forp>0, thep-Berezin integral transform ofgon generalized Fock space is defined to be B(ψ,φ)(|g|p)(w)= |g′(z)φp,φ(|z|)|pdv(z). One of the main tools in proving our results is the following theorem which comes from the Corollary 11 in Constantinetal.’s paper[17]. A direct computation shows that (5) for positive constantsc,C. If the weight function satisfies then by L’Hospital’s rule, we get By the same way, if we choose that function such that then Obviously the above discussion contradicts the condition (5). So we can see that the weight function has a property that Moreover,φ(z)does not grow faster than |z|2and decay more slowly than |z|2at infinity. At this time, it is easy to check thatφ(r)satisfies the so calledKp-condition for constantK>0. Then the following theorem holds according to Ref.[17]. Theorem2.1Assume that 0 for any entire functionf. The following estimate is important to our main results. Lemma2.2For eachp>0, letμ(p,φ)be the positive pull-back measure onCdefined by μ(p,φ)(E)= for every Borel subsetEofC. Then whereD(w,1) is the disc with centerwand radius 1. ProofFor eachz∈D(w,1), by (2), (3) and (4), we have This shows that The definition of the measureμ(p,φ)and the integral transformB(ψ,φ)(|g|p) give that |g′(z)φp,φ(|z|)|pdv(z)≈ B(ψ,φ)(|g|p)(w). The proof is finished. Now we state our first main result. Theorem2.3If 0 (6) Proof(i) Suppose that the operatorV(g,ψ)is bounded. For 0 On the other side, ‖kw,φ‖p,φ This means ‖kw,φ‖p,φ≈1. Thus, by applyingV(g,ψ)on the normalized kernel functions along with Theorem 2.1, Then we get the necessity part. To prove the sufficient part, we extend the techniques used in Refs.[6,16]. Combining the definition of the measureμ(q,φ), Theorem 2.1 and Theorem 2.1 in Ref.[18], we can get Lemma 2.2 and Fubini’s theorem show that (ii) Note thatkw,φ→0 as |w|→∞ uniformly on any compact subset ofCand ‖kw,φ‖1 for allw, thenkw,φ→0 as |w|→∞ then weakly infor 0 It means that necessity follows. For a fixedR>0, we set Secondly, we prove the similar conclusion for the second piece of the integralIn2. It follows from the conditions ‖fn‖p,φ1 for allnandB(ψ,φ)(|g|q)(z)→0 as |z|→0 that In general, it is difficult to characterize the boundedness, compactness, or Schatten class membership of a concrete operator with proper conditions. For reproducing kernel Hilbert spaces, the Berezin type transforms often are useful conditions, partly because we can know the effect of their action on the kernel functions, this is called the operator theoretic method. However, nobody can completely interpret why, how and when these conditions are effective. The boundedness and compactness ofV(g,ψ)are respectively equivalent to A natural question is whether there exists an interplay between the two symbolsgandψinducing bounded and compact operatorsV(g,ψ). We first observe that ifg′≠0, then by the classical Liouville’s theorem the functiongcannot decay in any way. This forces that is bounded only whenψ(z)=az+bwith |a|≤1. Moreover, if |a|=1 thenb=0, and compactness is achieved when |a|<1. Then the following corollaries hold. In general, the boundedness of operatorV(g,ψ)does not necessarily imply that the Volterra type integral operatorVgis bounded. This is because that the boundedness of the former allowsgto be any entire function that grows more slowly than the exponential part of the integrand in {B(ψ,φ)(|g|p)(w)}, while the boundedness of the latter forcesgto grow as a power function of at most degree 2, as can be seen below. By settingψ(z)=zin the theorem, we immediately get the following result. (i) bounded if and only ifg(z)=az2+bz+c,a,b,c∈C; (ii) compact if and only ifg(z)=az+b,a,b∈C. B(ψ,φ)(|g|q)(w) |g′(w)φp,φ(|w|)|q (7) where D(w,1)={z∈C:|z-w|<1}. The boundedness ofV(g,ψ)implies|g′(w)φp,φ(|w|)|1 for allw∈C. In terms of the growth ofφp,φ(|z|) at infinity andgis entire function, the desired expression forgfollows. |g′(z)φp,φ(|z|)|→0, |z|→∞. This can happen only whengis a polynomial of degree at most 1. Ifψasψ(z)=βzwith |β|<1, thengcan have loose condition. More precisely, we get the following corollary. For the case 0 Theorem2.7Let 0 (8) ProofIt’s obvious that (ii) implies (i), then we just need to show that (iii)⟹ (ii) and (i) ⟹ (iii). Firstly, if we assume that we can see that whenR→∞. This shows thatV(g,ψ)is compact. Now our proof will be complete once we show that (iii) follows from (i). To this end, note thatV(g,ψ)is bounded if and only if However, it’s easy to see that where dλ(q,φ)(z)=eqφ(z)dμ(q,φ)(z). The above inequality means that dλ(q,φ)is a (p,q) Fock-Carleson measure. By Theorem 2.8 in Ref.[19], this holds if and only if Substituting back dλ(q,φ)and dμ(q,φ), we obtain from (2), (3) and (4) that B(ψ,φ)(|g|q)(w). It remains to prove the estimate (8). Sinceλ(q,φ)is a (p,q) Fock-Carleson measure, the series of norm estimates in Theorem 2.8 in Ref.[19] yields This ends the proof. It is interesting to note that unlike condition (i) of Theorem 2.3, where we map smaller spaces into bigger ones, condition (iii) above is expressed in terms of both exponentspandq. Whenψ(z)=z, the theorem simplifies to saying thatVg(for non-constantg) is bounded or compact if and only ifg′ is a constantq>2p/(p+2) andg′=0 forq<2p/(p+2). This is because by subharmonicity, we have from which the desired restrictions ong,pandqfollow once we assume that the left-hand side of above inequality is finite. The essential norm ‖T‖eof a bounded operatorTon a Banach spaceBis defined as the distance fromTto the space of compact operators onH. We refer to Refs.[13-14,16,20-21] for estimation of such norms for different operators on Hardy space, Bergman space,Lp, and some Fock spaces. Here we estimate the essential norm ofV(g,ψ)as following. Then we have Lemma3.2Let 1 and |Rnf(w)|→0 uniformly on any compact subset ofC. ProofBy Corollary 3 in Ref.[22], we know that there exists constantMsuch that for anyn∈Z+. Then Proposition 1 in Ref.[22] shows that It is obvious that |Rnf(w)|→0 uniformly on any compact subset ofCfrom the properties of Taylor series of entire function. V(g,ψ)=V(g,ψ)(Rn+Kn), we have ‖V(g,ψ)-K‖≤‖V(g,ψ)Rn‖+ ‖V(g,ψ)Kn-K‖ (9) where the equality comes from compactness ofQ. This shows the lower estimate in the theorem. In1+In2, whereRis fixed positive number. We first estimateIn1as follows. Firstly, we have By Lemma 3.3, we get This completes the proof. Let us now characterize the operatorV(g,ψ)in the Schattenp-class membership for 0 (i) Ifp≥2 andT∈Sp, then (10) (ii) If 0 (11) We know thatTbelongs to the Schatten classSpif and only if (T*T)p/2is in the trace class. Thus Tr((T*T)p/2)= for 2≤p<∞, and for 0 which gives the proofs of the necessity forp≥2 and the sufficiency for 0 (12) for allz∈C. Then we define the following Toeplitz operator by V*(g,ψ)V(g,ψ)f(z)=〈V*(g,ψ)V(g,ψ)f,Kz,φ〉φ=〈V(g,ψ)f,V(g,ψ)Kz,φ〉φ= dμ(z)=ζ∘ψ-1(z)dv(z), where ζ(z)=|g′(z)|2|φ2,φ(|z|)|2e2φ(ψ(z))-2φ(z). Thus the result of this theorem holds. ProofIfVgis a compact operator, then by Corollary 2.5,g′=C, a constant. By (2) and Hölder’s inequality, we have IfVgbelongs toSp, then the above integrals should converge for allp>2.




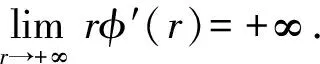


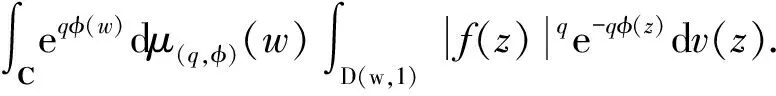

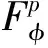


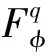
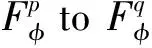








3 Essential norm of V(g,ψ)on generalized Fock space

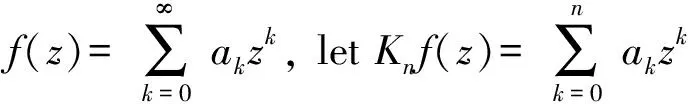
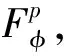


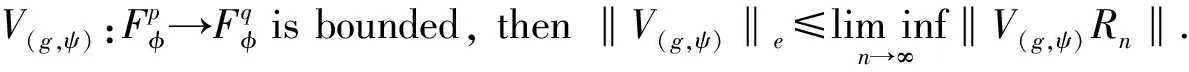

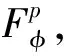
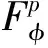

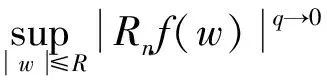
4 Schatten p-class operator V(g,ψ) on generalized Fock space