链式弹仓冲击力与疲劳特性研究

赵慧文，韩晓明，李 强，段肖娜，余朝发

(1.中北大学 机电工程学院， 太原 030051； 2.山西北方机械制造有限责任公司， 太原 030009；3.陆军工程大学 军械士官学校， 武汉 430000)

从20世纪60年代开始,以美俄为首的西方国家逐步开始了弹药自动装填的探索,逐步实现了弹药的自动装填,至80年代后期,已有多国装备了能够实现弹药全自动装填的大口径火炮,自动装填系统经过几十年的更新换代,形式和技术也得到了长足的发展[1]。链传动弹仓是一种常用的供弹机构，链传动的输弹形式应用很广，相应的研究也很多。李晓等[2]提出一种大节距轨迹约束型输送链约束轨迹的补偿方法。构建了一种大节距轨迹约束型输送链模型，建立了静态下一个周期内链条销轴的位置变化，并得到静态下可以满足装配要求的约束轨迹。为其多边形效应的研究打下基础。张玲玲等[3]通过实验的方法对链传动多边形效应进行了深入研究。由于链条运动速度不稳定，使得主从动链轮的角速度不恒定，瞬时传动比不稳定。其他因素,例如链轮齿数、链条节距等对链传动的多边形效应也有明显的影响。王国晋等[4]基于多边形效应的影响，分析了不同形状的约束滑道对输送链运动过程的影响。许雷等[5]基于ADAMS，分析了特氟龙输送带的链传动多边形效应。杨仁民等[6]构建了链传动多边形效应实时传动数学模型，并利用ADAMS软件进行了实体仿真，对比了两者的差异性。倪健健等[7]基于多体动力学的理论，使用 ADAMS 软件对链条进行了仿真,分析其振动冲击状况，并得到其速度和加速度曲线，对于链传动系统的优化设计具有重要的指导意义。

在保障弹体运行平稳的前提下，还需验证冲击力的大小对链机构使用寿命的影响。

1 链传动机构及运行轨迹分析

1.1 链传动机构理想模型的建立

因为无轨迹约束型链传动机构的运动没有规律性，所以对普通无轨迹约束链条的静态分布及动态分析会变的没有意义。轨迹约束型链传动机构的静态分析相对简单。链条由于多边形效应的存在，无约束状态下会不规则运动。轨迹约束的好处就在于让链条按照预定的轨道运动，减小了其垂直于运动方向的运动，能提高链条的整体性能，根据某型号弹药参数，设计的轨迹约束型输送链传动弹仓机构实体模型如图1。

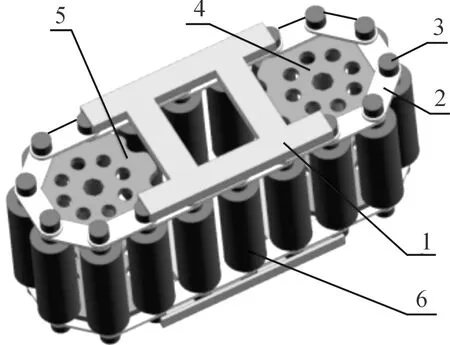
1.销轴固定导轨；2.输弹链条；3.销轴；4.从动链轮；5.驱动链轮；6.容弹器

通过对输送链的抽象简化，建立如图2所示的理想轨迹约束型输送链模型，在理想模型中，用一段直线Ji-Ji+1表示链节，其中J为连接各个链节的销轴，图2中轨迹线条即为链条的运行轨迹。将链传动机构中的销轴视为质点后，就变成了对有限个按照一定规律分布的质点的研究。该结构共18个链节。

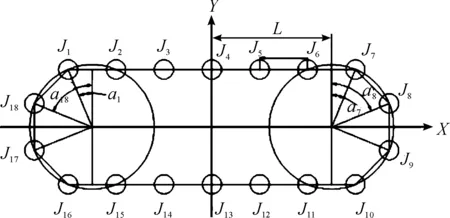
图2 轨迹约束型输送链的理想模型

1.2 链传动机构销轴轨迹坐标分析

链节长度为L=250,左右两个链轮大小相等(左轮为驱动轮，右轮为从动轮)，轮半径Rq=325,单个链节在链轮上所占角度为π/4，从动轮圆心的横坐标ST=950-Rq,为方便计算，令a1、a7、a8、a18分别指销轴J1、J7、J8、J18与y轴正方向的夹角，以此类推剩余销轴与y轴正方向夹角。xn、yn分别表示第n个销轴的横坐标与纵坐标值。

链条逆时针旋转时，销轴J1的静态坐标：

1) 销轴J1在驱动轮上

2) 销轴J17在驱动轮上

3) 销轴J7在从动轮上

4) 销轴J9在从动轮上

5) 销轴J16在下轨迹上，可得J16、J17的位置关系

6) 其余销轴的静态坐标可由销轴J1、J7、J10、J16静态坐标类推得到，上轨迹销轴与销轴J1、J7纵坐标相同，横坐标以间隔L递变；下轨迹销轴与销轴J10、J16纵坐标相同，横坐标以间隔L递变。

1.3 链传动机构运动状态分析

轨迹约束型链传动机构，若按照理想状态下静态位置来设计轨迹约束，链传动机构会卡死而无法运转，因此在链条销轴平动阶段利用轨道约束其运动轨迹，在随链轮运转阶段，依靠链轮的约束力来实现正常的运转。

链条多边形效应的根本原因在于与主从动轮啮合的销轴运动速度不一致，因此对链传动机构的分析主要针对链条绕上主动轮、绕下主动轮、绕上从动轮、绕下从动轮4个过渡位置。其中绕上主动轮和绕下从动轮的销轴运动状况决定上轨迹的补偿，绕下主动轮和绕上从动轮的销轴决定下轨迹的补偿。根据链传动的多边形效应，在一个周期内，左右链轮上销轴的有效速度均不相等，在链条运动方向上的位移也不相同[8]。

1) 上边在驱动轮上的运动分析

图3为销轴J1的速度分析，其中Vr表示实际速度，方向垂直于链轮中心与销轴J1的连线，V1为链条运动方向的速度，即有效速度，通过图中的数学关系易得有效速度

V1=Vrcos(a1r)

而销轴J1的位移为

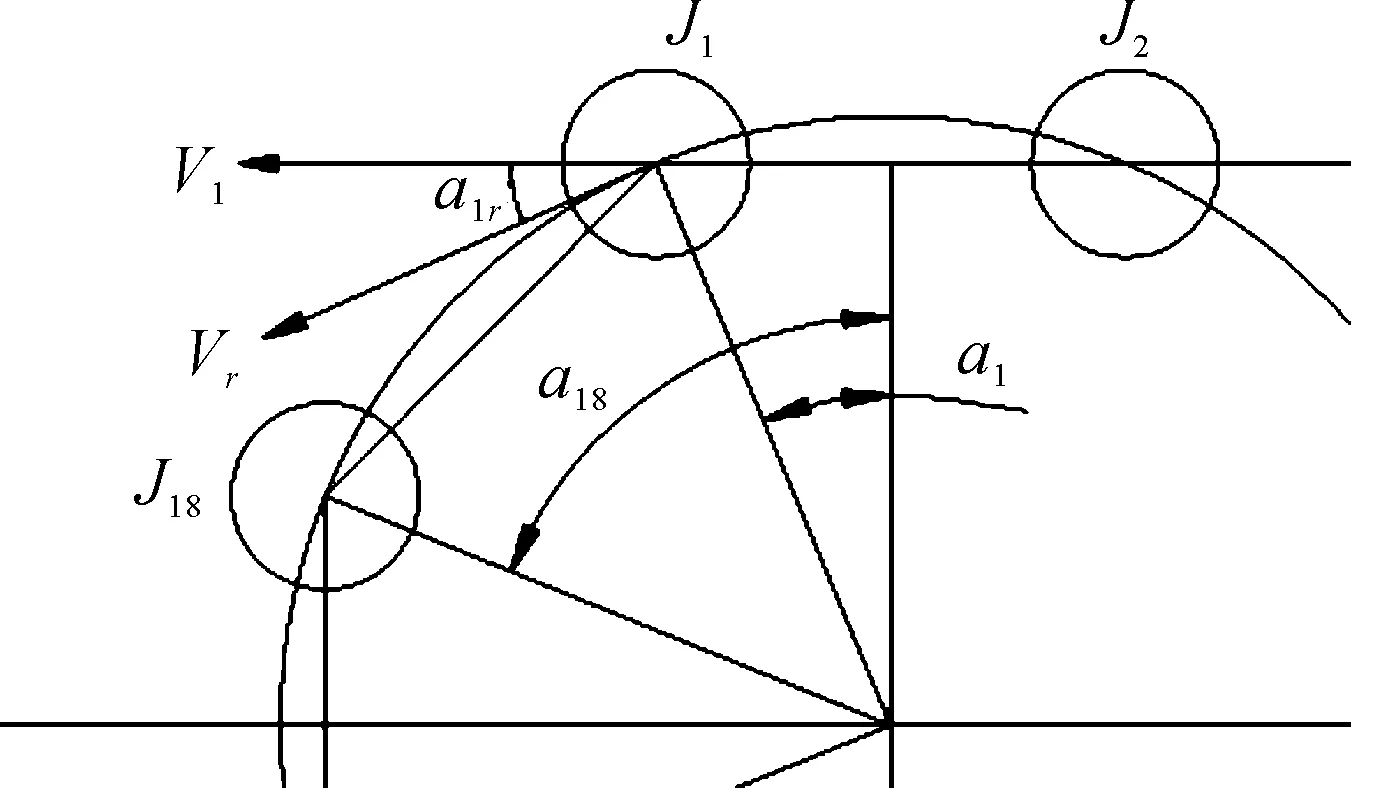
图3 上边在驱动轮上的速度分析

2) 上边在从动轮上的运动分析

图4为销轴由从动轮绕上上边的速度分析，销轴J7、J8均可能由从动轮绕上上边，因此有效速度为

V2=V2rcos(a2r)

销轴的位移为

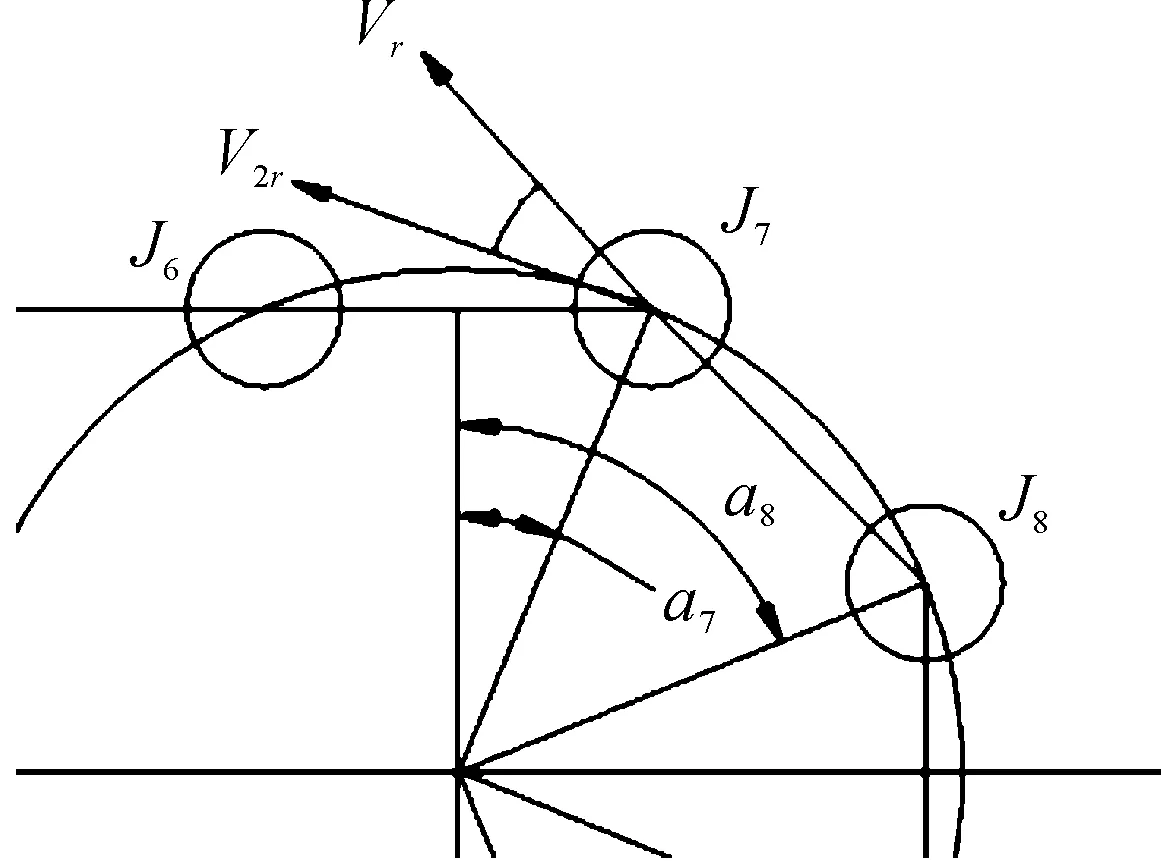
图4 上边在从动轮上的速度分析

3) 下边在驱动轮上的运动分析

图5为销轴由从动轮绕上上边的速度分析，销轴J17均可能由从动轮绕上上边，因此有效速度为

V3=V3rcos(a3r)

销轴的位移为

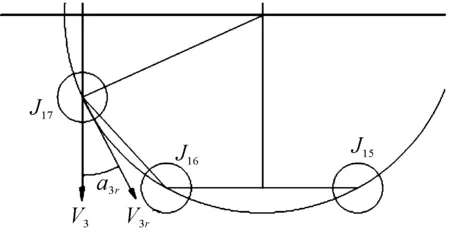
图5 下边在驱动轮上的速度分析

4) 下边在从动轮上的运动分析

图6为销轴由从动轮绕上上边的速度分析，销轴J10、J11均可能由从动轮绕上上边，因此有效速度为

V4=V4rcos(a4r)

销轴的位移为

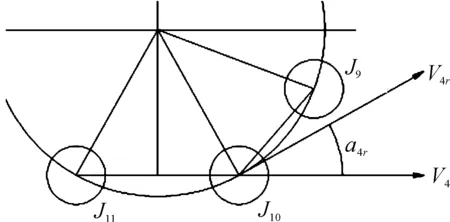
图6 下边在从动轮上的速度分析

2 链条结构疲劳寿命理论分析

疲劳破坏是工程结构和机械失效的主要原因之一，引起疲劳失效的循环载荷的峰值往往远小于根据静态断裂估算出来的安全载荷，因此开展结构疲劳研究有着重要的意义[9]。

ANSYS疲劳分析采用了经典的Miner线性累积损失理论。

若构件在某恒定应力S作用下，循环至破坏的寿命为N，则定义其在经历n次循环时的损伤为

D=n/N

显然，在某恒定应力S作用下，若n=0,则D=0,构件未受疲劳损伤；若n=N,则D=1,构件发生疲劳破坏。

构件在应力Si作用下，经历ni次循环的损伤为Di=ni/Ni。若在K个应力Si作用下，各经历ni次循环，则定义其总损伤(ANSYS中称作疲劳寿命使用系数)为

破坏准则为

这就是Miner线性累积损伤理论。其中，ni是在应力Si作用下的循环次数，Ni是在应力Si作用下循环至破坏的寿命，由S-N曲线确定[10]。

3 链传动机构多体动力学仿真分析

3.1 弹链多边形效应的产生

无轨迹约束型链传输机构虚拟样机简化模型如图7所示,与销轴固连的容弹装置,在脱离链轮约束后,由于链条多边形效应的影响,运行轨迹会变得杂乱无章，轨迹约束型链传输机构虚拟样机简化模型如图8所示。

图7 无轨迹约束链输弹装置虚拟样机简化模型

图8 轨迹约束型链输弹装置虚拟样机简化模型

链条多边形效应的根本原因在于与主从动轮啮合的销轴运动速度不一致，驱动轮转速恒定，从动轮转速呈周期性变化。驱、从动轮转速随时间的变化曲线如图9。

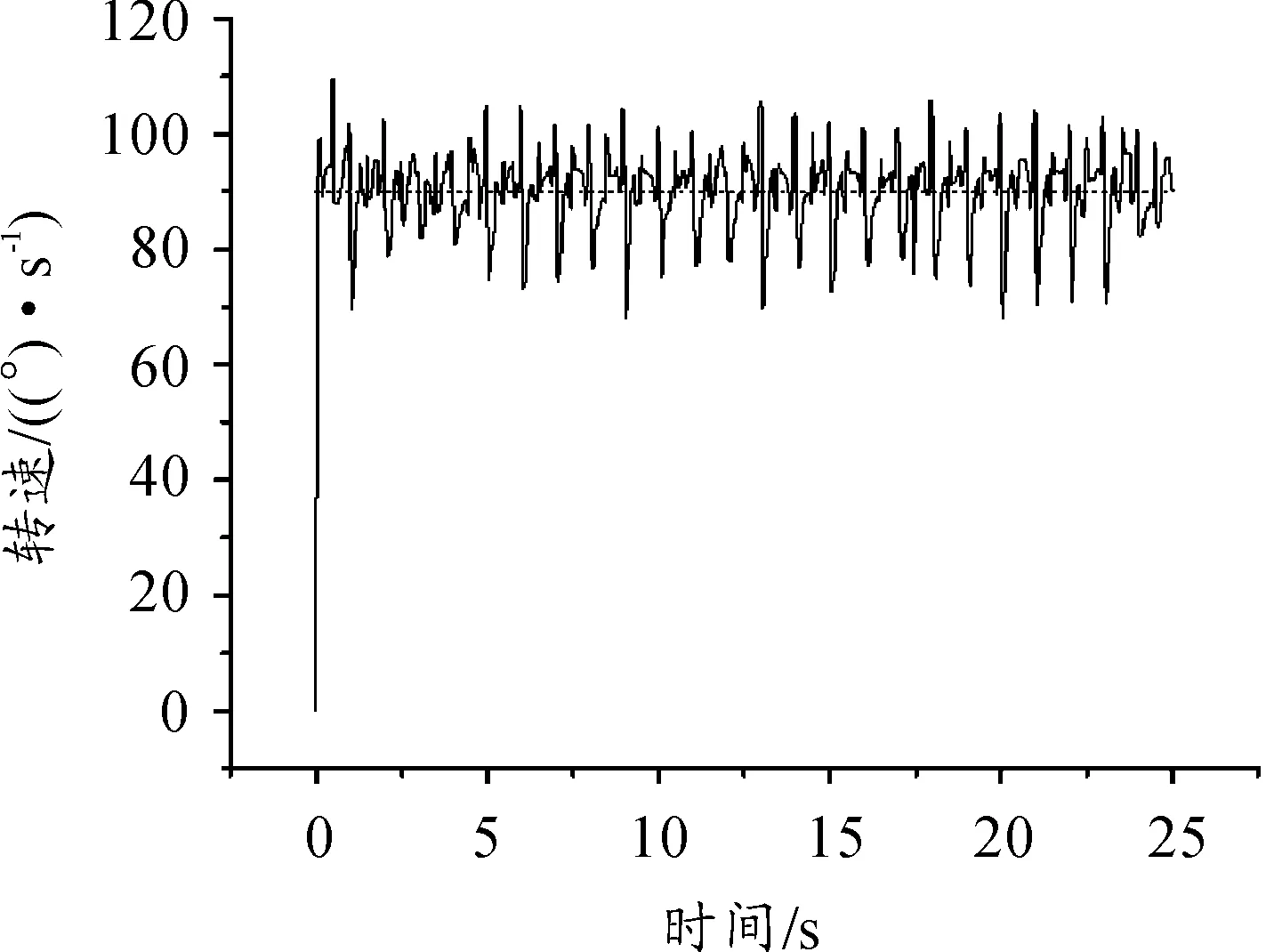
图9 驱、从动轮转速随时间变化的曲线

在多体动力学仿真软件ADAMS的仿真结果中,在无轨迹约束段,弹体的运行轨迹如图10所示；轨迹约束下的弹体运行轨迹如图11所示。

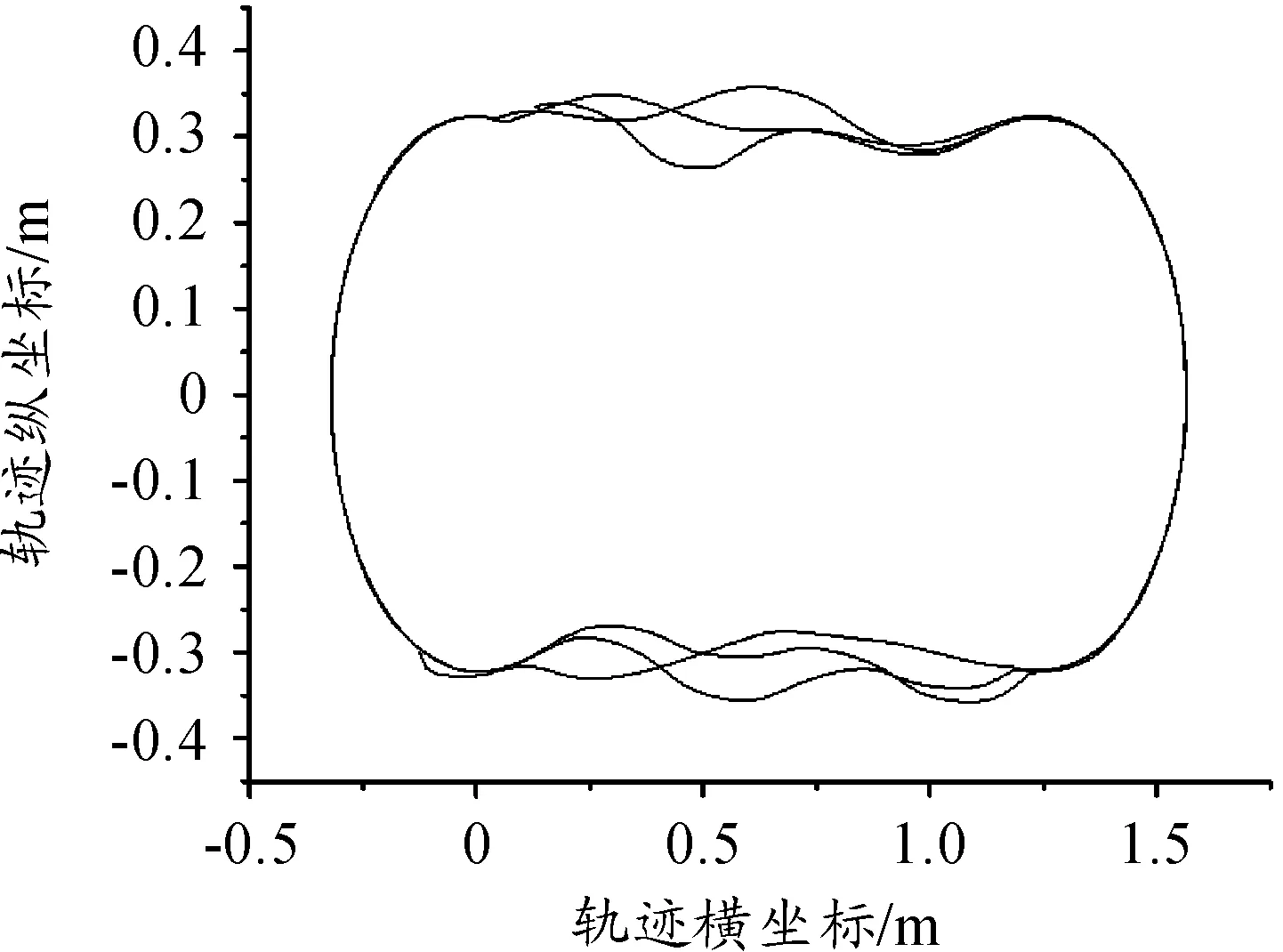
图10 无轨迹约束型弹体运行轨迹

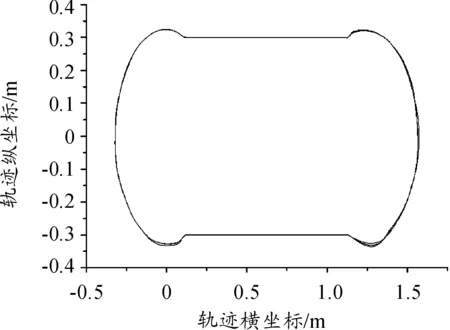
图11 轨迹约束型弹体运行轨迹

轨迹约束型链传输机构能很好的克服链条的多边形效应，弹体的运行更加平稳。

3.2 链条受多边形效应影响所受冲击力

输弹装置在运行过程中,各销轴的运行速度呈周期性变化,相邻销轴会呈现周期性的速度差,因此,链条会承受周期性的挤压与拉伸，这是链条间产生冲击力的原因。相邻销轴速度随时间变化的曲线如图12。

链条无约束链输送机构中所受冲击力随时间变化曲线如图13，链条在轨迹约束型链输送机构中所受冲击力随时间变化的曲线如图14。

无约束链输送机构中链条所受冲击合力峰值为130 N，轨迹约束型链输送机构中链条所受冲击合力峰值为300 N。轨迹约束型链传输装置中链条所受冲击合力会大幅增强，且冲击力也更为密集。

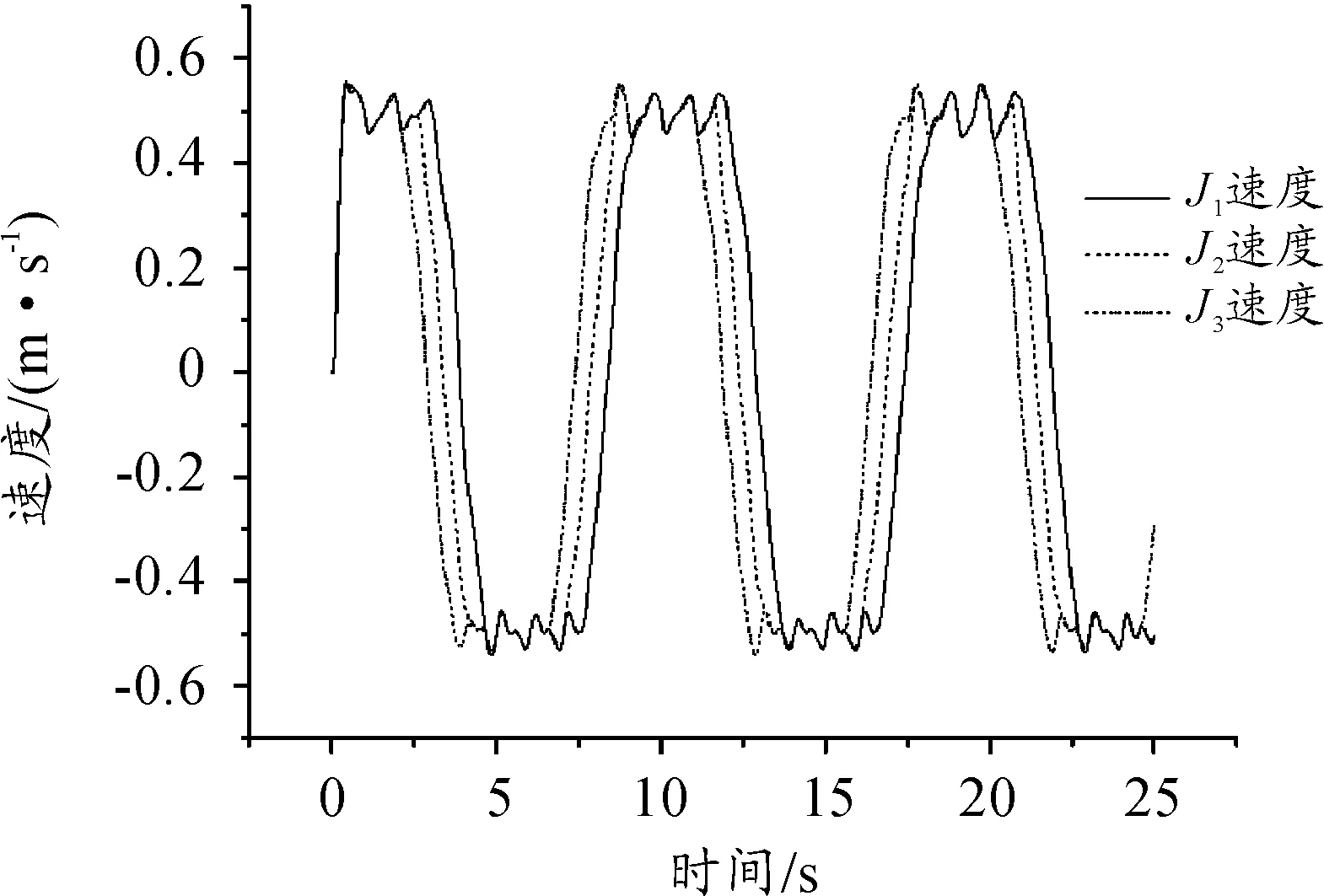
图12 销轴速度随时间变化的曲线

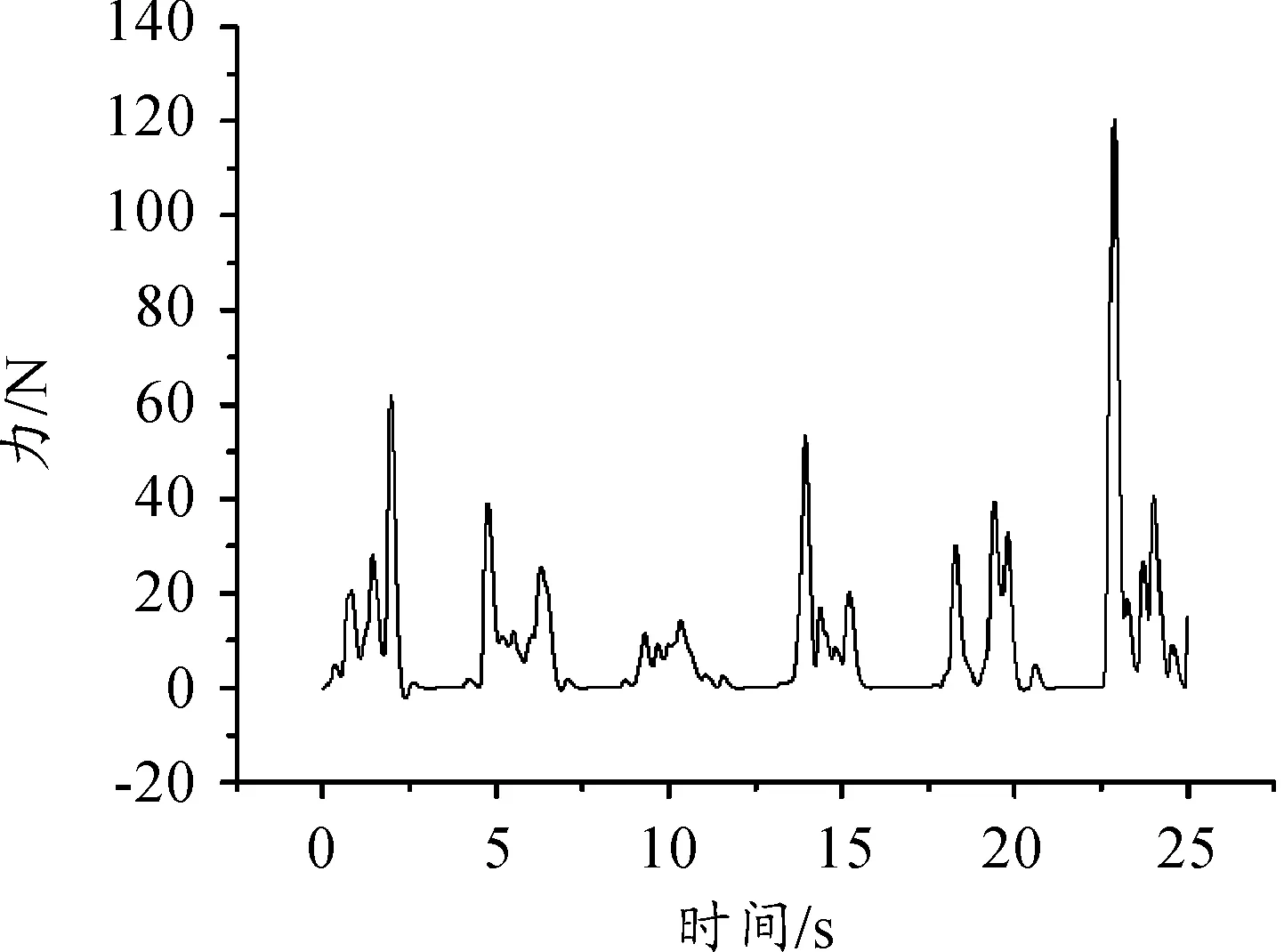
图13 无约束链输弹机构中链条所受冲击合力随时间变化曲线

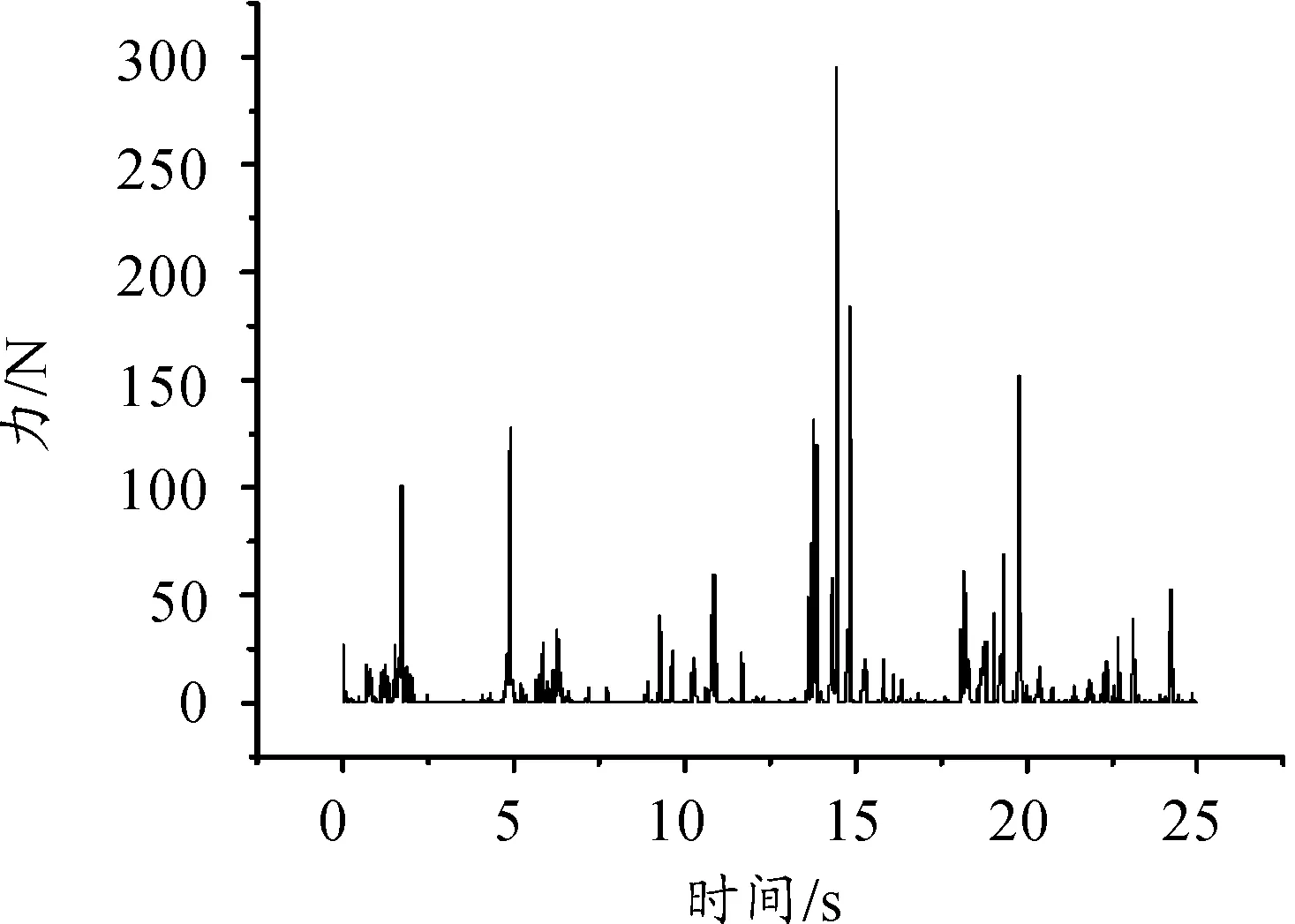
图14 轨迹约束型链输弹机构中链条所受冲击合力随时间变化曲线

3.3 多边形效应对链条使用寿命的影响

通过以上多体动力学的仿真分析可知，轨迹约束型链传输机构中链条所受冲击力大幅上升，为了分析冲击力的跃升对链条使用寿命的影响，利用ANSYS有限元软件对链条实体模型进行网格单元划分，施加约束，施加链条所受冲击载荷，可得链条应力分布云图，由于链条所受冲击在两内环处对称，节约运算时间，只运算一端内环所受冲击的情况。链条材料的S-N特性曲线如图15。

施加无约束链传送机构中链条所受的峰值载荷时，在应力云图中可得到应力最大值点处的应力值，该点发生疲劳破坏的可能性最大，如图16所示。借助ANSYS有限元软件对链条施加10 000次重复载荷冲击，计算得出链条的疲劳寿命使用系数为0.000 91。

施加轨迹约束型链传送机构中链条所受的峰值载荷时，同理，在应力云图中可得到应力最大值点处的应力值，该点发生疲劳破坏的可能性最大，如图17所示。借助ANSYS有限元软件对链条施加10 000次重复载荷冲击，计算得出链条的疲劳寿命使用系数也为0.000 91。

因此，在有效次数冲击合力的反复作用下，两种冲击力对链条的疲劳寿命影响很小，可以忽略。

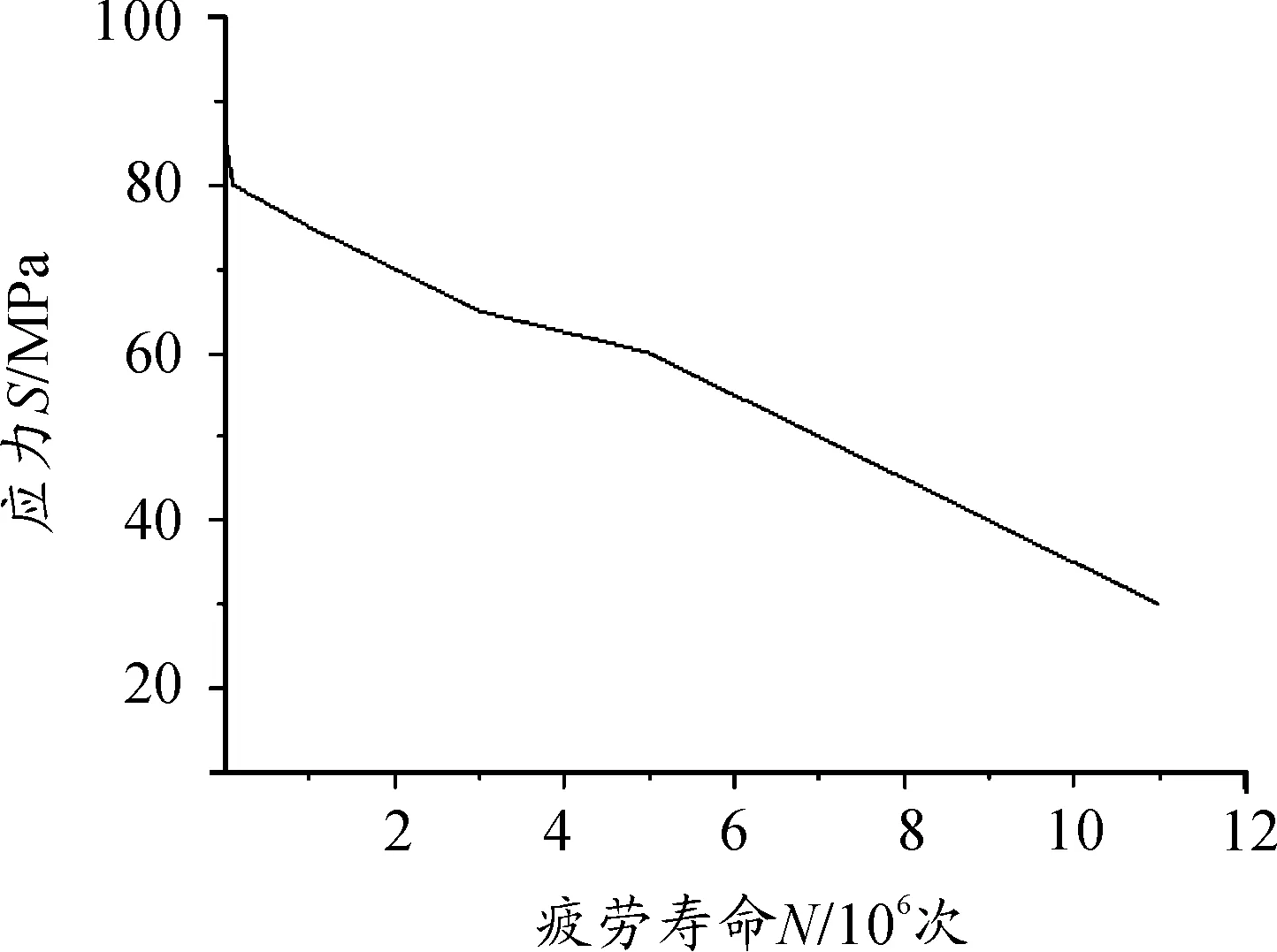
图15 链条材料的特性曲线

图16 无轨迹约束链条应力云图及ANSYS运算结果

4 结论

1) 自由型链传动机构中弹体的运动杂乱无章，加装约束导轨后，弹体的运动变得平稳而有序。

2) 弹体自由运动段加装约束导轨的轨迹约束型链传动机构，可以有效的克服多边形效应对弹体运动的影响，弹体的运输过程更加平稳可靠；虽然轨迹约束下链条所受冲击合力大幅增长，且作用的更加密集，但对链条疲劳寿命影响极小，可以忽略。

3) 轨迹约束型链传动机构能够有效克服弹链的多边形效应，使自动供弹弹仓中弹体的运行平稳有序。