基于强化路面的车身疲劳联合仿真

李高伟，王显会，张 明，周云波，孙晓旺，樊晓都

(1.南京理工大学 机械工程学院， 南京 210094； 2.东风汽车公司技术中心， 武汉 430056)

2017年，我国汽车总产量达到2901.54万辆，各厂商不断推出新车型，同时有些汽车因零部件出现疲劳裂纹等问题导致车辆被召回，存在安全隐患。在新车型开发初期，通过疲劳耐久性仿真分析，优化产品设计，满足车辆耐久性要求，缩短产品的设计开发周期。新车设计为检测车辆结构可靠性，需要在试验场完成路试实验，强化路面的高频激励在可靠性实验中具有重要作用。本研究建立石块路和波形路两种强化路面，通过仿真分析验证路面建立的可行性，以及应用材料信息库和材料修正模型，增加仿真的准确性。

国外在多种软件平台实现联合仿真有了一定的进展，并讨论了车辆各个系统之间的连接类型对仿真结果的影响。Yi和Darren等[1]对焊点做仿真分析，得到一种对汽车焊点疲劳分析很适用的一种方法。H.S，H.J和Kim C B[2]将刚柔耦合应用于疲劳仿真动力学模型，仿真得到载荷谱，完成整车疲劳仿真分析。Lin和Shan等[3]研究分析悬架系统的建立，对仿真分析具有一定的影响。Edar等[4]通过仿真分析建立虚拟试验场，为仿真分析得到载荷谱提供了一种路面激励。Dannbauer等[5]利用有限元、多体动力学和虚拟迭代等技术联合仿真，应用新的方法完成汽车疲劳寿命分析。国内在刚柔耦合的多体动力学模型的验证较多，刚柔耦合的模型在仿真实验中更加的贴近实际。通过实际实验获取车体所用材料的属性信息。曹建[6]利用实车疲劳耐久性试验获取载荷谱，仿真对标，得到部件的载荷谱。张瑞俊和尹亚平[7]等以载荷和材料属性为变量，分析某型车悬架疲劳损伤的原因。柳亮等[8]应用实测获得载荷谱数据，结合CAE技术，进行疲劳寿命分析。冯亚杰[9]建立某车型的刚柔耦合的多体动力学模型，获取目标模型不同路面激励下的载荷谱。

上述文献中分别研究了多体动力学模型建立在疲劳分析中的应用和其他一些影响仿真精度的仿真方法研究，但所应用的仿真路面大部分为根据国家标准GB7031-86自动生成的8级路面。本研究应用试验场路面的高程信息，建立强化路面，应用高频激励模拟军用车辆在战场环境下的疲劳寿命。

1 强化路面分析及疲劳分析方法

强化路面主要包括搓板路、石块路，卵石路、扭曲路、坑洼路等，试验场路面采集高程信息可采用惯性参照道路纵断剖面检测系统[9]。基于有限元方法的疲劳仿真分析主要应用疲劳分析理论进行疲劳寿命分析，主要的疲劳分析方法有名义应力法、局部应力一应变法、裂纹扩展法、频域分析法等[10]。

1.1 强化路面建立

搓衣板路是通过不同规格的条形长方体组成并在上方铺设等厚度柏油所形成的路面。其尺寸信息如图1所示。

示意图中矩形条为搓衣板路上的条形长方体，D为相邻两个条形长方体间距，约为600～620 mm，W为条形长方体的宽度，约为400～420 mm，H为条形长方体的高度，约为13～18 mm。

搓衣板路仿真载荷谱如图2所示。

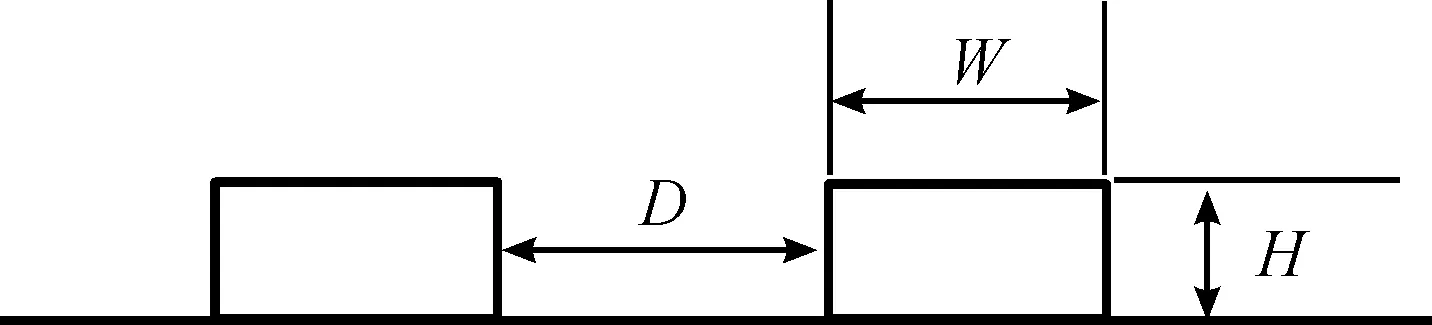
图1 搓衣板路示意图

图2 搓衣板路仿真载荷谱

石块路又称为比利时路，路面根据石块大小和间距分为重型、中型和轻型3种路面，为保证各级路面可以按比例混合比利时路面，一般比利时路面建成宽为4 m，长为50 m的统一规格的石板块[11]。建立的仿真比利时路面石块沿车行驶方向均匀分布，比利时路所用石块信息如表1所示。

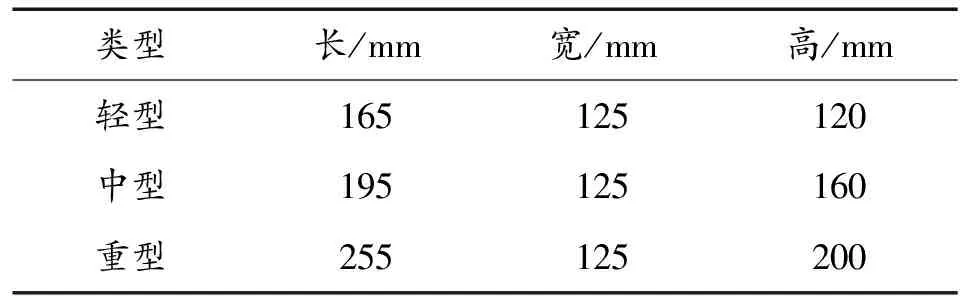
表1 比利时路石块信息

比利时路面示意图如图3所示，其中W为路宽，约为4 mm。

图3 比利时路面示意图

1.2 疲劳分析方法

根据对载荷谱处理方式的不同，分为静力学分析法和频域分析方法[12]。静力学分析法为根据采集的应力或应变随时间的变化曲线，结合有限元的静力学分析结果进行疲劳分析。频域分析法是将载荷谱的时域信息转化为频域信息，将载荷谱转化为应力功率谱，结合车身结构的模态和频响分析结果，完成基于频域的疲劳分析。对于大时长和考虑较多的加载载荷信息时，应用频域分析法计算效率更高[13]。本文主要研究基于搓衣板路和石块路的车身疲劳分析，选用时域分析方法。

时域分析方法需要考虑外部载荷激励和有限元静态分析，根据有限元模型的静态分析结果进行多个载荷通道的加载输入，即为根据多体动力学计算获得的外界输入载荷历程，与有限元分析中单位载荷作用的静态应力分析结果相乘叠加求和计算得到的结构动应力，可以用以下公式表示

(1)

其中：Pk(t)为载荷时间历程；Pk,fea为静载荷情况下力的大小；σi, j, k为加载k作用下点ij的静态力。

在线性疲劳累积损伤理论中，应用最为广泛的为Miner法则。该理论假设每个应力激励对材料的影响相互独立，总损伤则线性叠加[14]。Miner 法则假设：材料当疲劳损伤累积到一定值就会发生疲劳破坏。假设材料吸收能量达到W时放生疲劳破坏，此时总循环次数为N，当试样循环次数为ni时，吸收的能量为wi，则

(2)

假设某个构件加载L个不同的应力σ1，σ2,σ3,σ4,…,σL,对应L个不同的疲劳寿命N1，N2,N3,N4,…,NL其循环的次数为n1，n2,n3,n4,…,nL,则构件的损伤为

(3)

当吸收的能量达到W时，试件发生疲劳破坏。

根据静态试验数据，构建材料S-N曲线，并应用Goodman方法修正，因采用全寿命分析方法，进行疲劳寿命评估。全寿命分析法又称为名义应力法或应力-寿命法[15]。S-N曲线是指材料的应力和寿命的关系曲线。该方法主要应用材料的S-N曲线，参考部件的危险部位的应力集中系数以及名义应力，根据疲劳累积理论计算疲劳寿命[16]。

2 疲劳寿命分析

整车的疲劳寿命分析，综合多个软件平台的共同实现，为方便理解，对某型车的疲劳寿命分析的步骤如图4所示。

2.1 多体动力学仿真

多体动力学模型的建立准确性，决定仿真结果的准确性。应用刚柔耦合建立多体动力学模型，可以提高实验的精度[17]。建立弹簧、橡胶、阻尼器和一些可以变形杆件的柔性体模型，模型车辆的无相对运动的部件建立为刚性体。通过建立目标车辆的多体动力学模型，在Adams软件平台上实现运动学仿真。根据法规要求，仿真模拟多体动力学模型在两种强化路面下的试验工况，提取车身四个悬置处的六分力载荷谱数据，结果如图5和图6所示。

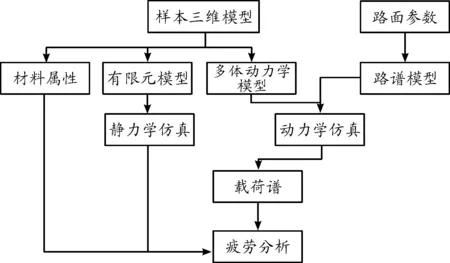
图4 分析流程框图

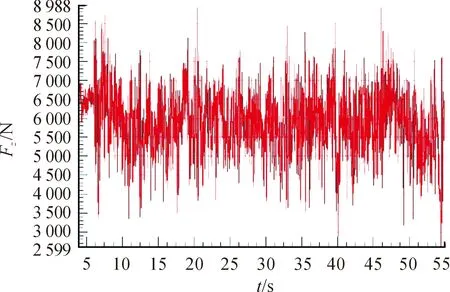
图5 车身右前Z向力载荷谱

图6 搓衣板路车身右前Z向力载荷谱

提取车身四个悬置点六分力载荷谱作为疲劳分析的载荷输入，为保证载荷谱加载连续性，应用Graphworks软件品台，对仿真数据进行处理。

2.2 有限元仿真分析

2.2.1有限元模型建立

需要对所分析目标车型进行有限元划分，为保证仿真精度，需要保证网格质量，焊点采用壳单元模拟[18]。

建立目标车辆的有限元模型，如图7所示。

对有限元模型网格质量进行控制，该有限元模型共包含507 542个单元，其中四边形单元有476 284个，三角形单元有2 600个和26 865个焊点单元，其中三角形单元占单元总数的0.54%，单元质量较好，所有车身结构零件的材料特性定义为线性弹性。

2.2.2有限元分析

基于静力学的疲劳分析方法，需要对车身的有限元仿真模型进行静力学分析。在车身四个悬置点分别加载单位六分力，对有限元模型进行静力学仿真，边界条件如图8所示。

图7 目标车辆有限元模型

图8 边界条件

有限元模型分析时，在车身每个悬置点处添加单位六分力，分别为三个方向力和三个方向的力矩，计算有限元模型产生的应力，包括最大主应力、等效应力和Tresca应力等，可以用来确定结构模型上每个单元或节点处的疲劳寿命。

静力分析中采用惯性释放的方法，即惯性释放的方法可以在施加虚假的反力约束，实现结构力作用的平衡，消除约束点的反力而提高计算精度[18]。当外力作用在部分或者完全没有约束的部件上时，会在自由约束的方向上产生刚体加速度，部件会受到惯性力的作用，运动方程为

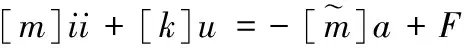
(4)

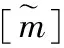
应用惯性释放的方法可省去查找约束的过程，在有限元计算中，约束不足或者约束过多将会导致计算结果不准确，采用惯性释放的方法在MSC.Nastran软件平台上对整车进行静力学分析，可提高有限元计算精度。

2.3 疲劳寿命分析

应用局部应变法(ε-N方法)和全寿命法(S-N法)分析某军用越野车白车身疲劳寿命。疲劳分析流程如图9所示。

图9 疲劳分析流程框图

疲劳分析中结构材料的准确性，关系到计算结果的准确层度，本研究所采用的材料源于实验室所建立的静态实验材料库，本研究中所应用的材料有防弹钢、大梁钢和Q235，其材料属性如表2所示。

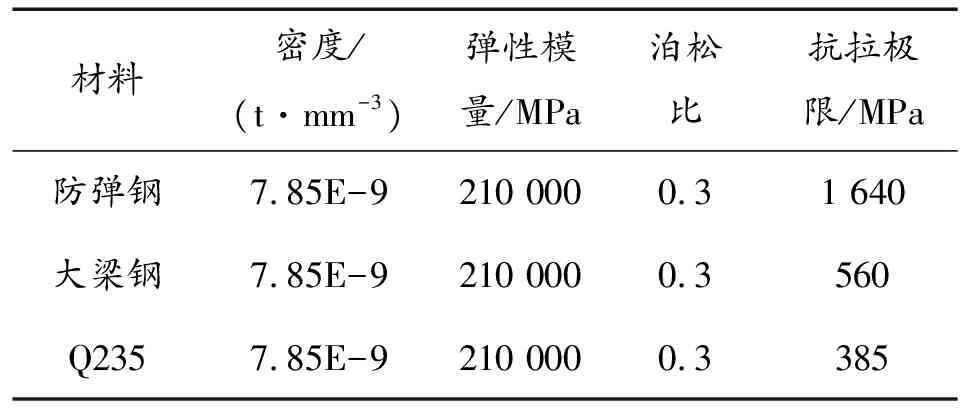
表2 材料属性

利用疲劳分析软件，导入仿真得到的载荷谱文件和有限元分析文件，设定材料的特性曲线，并赋予模型的各个部分，控制分析流程，得到疲劳寿命分析结果。

3 疲劳寿命结果分析

3.1 单位载荷下应力结果

单位载荷作用下车身应力云图如图10所示。

图10 单位载荷作用下白车身应力云图

3.2 全寿命法(S-N法)计算得白车身疲劳寿命

3.2.1满载工况

由图11和表3可以看出，在满载工况下车身最短的疲劳寿命为0.538 4×104个循环，发生疲劳破坏的位置在中通道左侧三块板焊接位置。

图11 满载工况白车身损伤分布

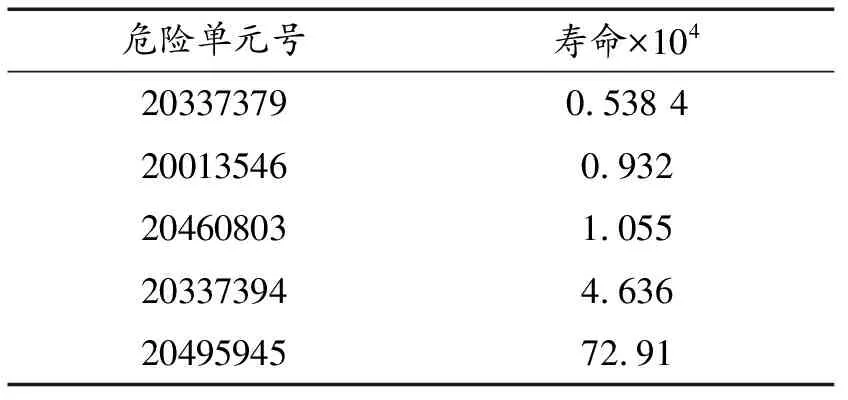
表3 满载工况部分危险单元号

3.2.2空载工况

由图12和表4可以看出，在空载工况下车身最短的疲劳寿命为1.473×104个循环，发生疲劳破坏的位置同样在中通道左侧三块板焊接位置。

在实车上找到对应位置，发现该位置由三块板拼焊而成，容易应力集中，在该位置增加焊缝补强板，改善该处的焊接缺陷。

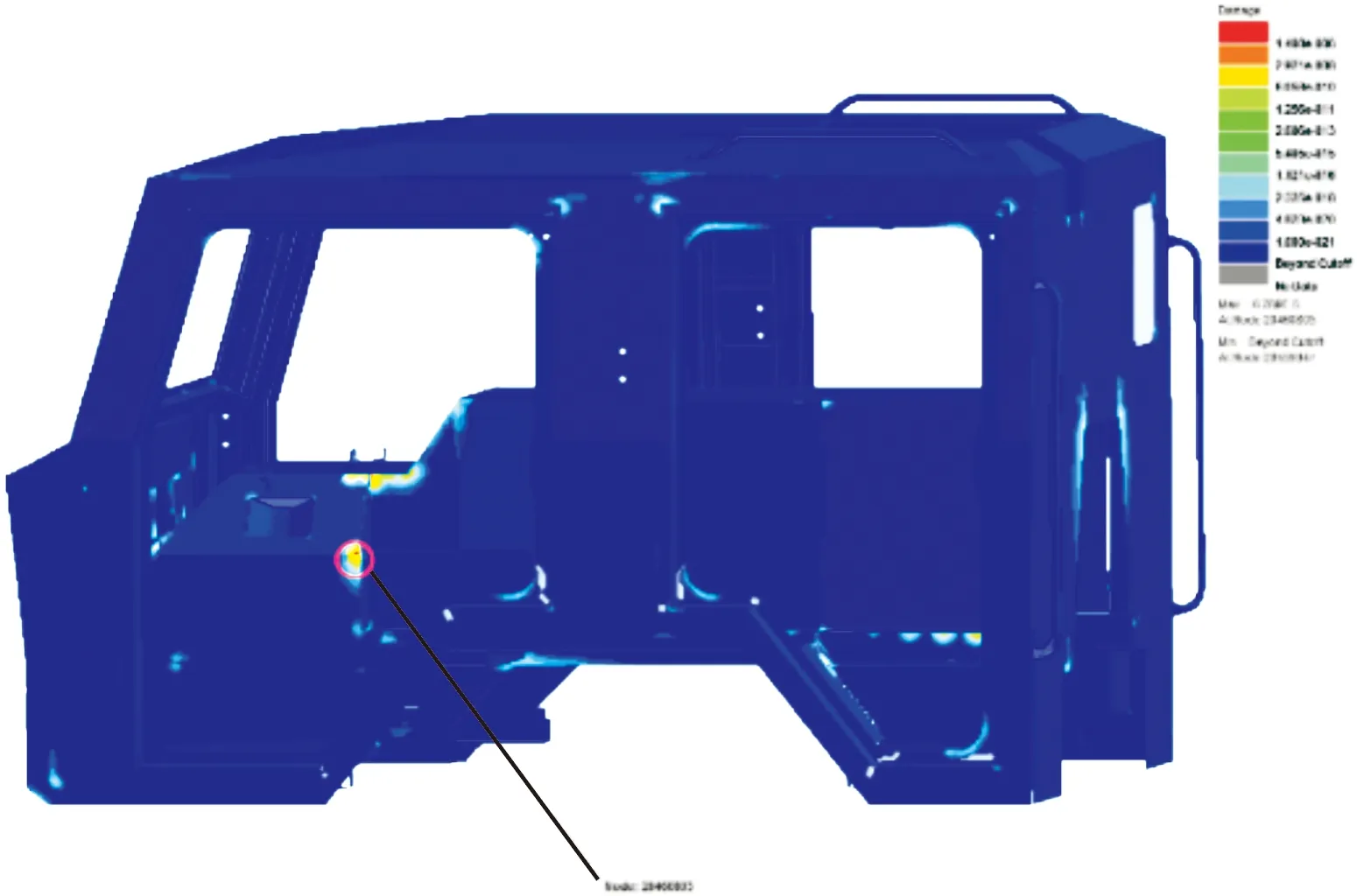
图12 空载工况白车身损伤分布

表4 空载工况部分危险单元号

4 结论

通过建立车辆在野外复杂路面受到高频激励的多体动力学模型，仿真得到车身悬置处的六分力载荷谱数据，以此为边界条件，结合静力学分析，完成对某型车的疲劳寿命分析。

根据分析结果在实车上找到相应位置，找到影响其寿命的具体原因，并进行改进，缩短产品开发周期，降低研发成本。战场路面环境复杂，需不断进行修正路面模型和统计车辆的行驶工况。