膨胀-劈裂组合模式下薄壁圆管的吸能性能研究

吴明泽，张晓伟，张庆明

(北京理工大学 爆炸科学与技术国家重点实验室， 北京 100081)

薄壁圆管具有高比强度、高比刚度和轻质量的特点，因此在抗冲击结构中得到广泛应用[1]。其中，轴向压缩条件下薄壁圆管的膨胀变形具有变形过程稳定、载荷平滑、对载荷方向不敏感等优点[2]，且膨胀压缩载荷可通过压模结构参数改变实现在较大的范围内调控，以满足不同载荷的载荷设计要求；但是，为了让薄壁圆管充分膨胀，膨胀结构中锥头压模的有效长度需得大于圆管的长度，导致膨胀机构在工作中的整体行程效率较低(<50%)。而对于薄壁圆管的轴向劈裂变形模式则具有行程效率高的优点，其行程效率能达到90%以上；但是，其平均载荷力较低，即使在75o的压模锥角下，其平均载荷力也仅为薄壁圆管渐进压溃模式平均载荷力的1/3[3-7]。学者们研究发现，通过一定的压模结构设计，能让薄壁圆管在轴向下压的过程中发生先膨胀后劈裂的组合变形模式，结合两种变形模式的优点，有效地提高薄壁圆管的吸能性能[8-10]。

对于薄壁圆管的膨胀-劈裂组合变形模式，其变形过程复杂，较难精确地给出结构吸能性能参数与影响因素之间的理论解析式。因此，本研究提出通过试验设计建立响应面模型(RSM)的方法[11-12]，去研究压模结构参数对组合变形模式下薄壁圆管吸能性能的影响。以比能量吸收率与最高峰值力为优化目标，对结构进行了优化设计。

1 吸能性能指标和模型的建立

1.1 吸能性能指标

薄壁圆管吸能性能主要通过以下指标进行衡量[11-12]：

1) 最大峰值力Fmax：薄壁圆管变形过程中沿轴向产生的最大载荷。为了减小载荷对乘员的伤害，应尽可能降低冲击过程中的最大峰值力。

2) 平均载荷力Fm:

(1)

式中：E为薄壁结构所吸收的总能量；S为轴向下压行程。

3) 比能量吸收率SEA:单位质量的吸能结构所吸收的能量。

(2)

式中：m为吸能结构有效变形阶段的质量。为满足结构轻量化的设计要求，薄壁结构的比能量吸收率应尽量大。

4) 吸能效率：即平均载荷力与最高峰值力的比值：

(3)

式(3)表征了结构的能量吸收平稳性，一定程度上也反映了材料的吸能利用率。

1.2 模型的建立

以内径Do=50 mm、厚度t=1.5 mm、长度L=200 mm的薄壁圆管作为研究对象。图1为膨胀-劈裂组合变形模式的机构示意图，薄壁圆管在轴向受压的过程中，压模的下锥面使圆管发生膨胀，压模的上锥面则使膨胀后的圆管管壁发生劈裂变形，两锥角之间的间距h=23 mm，压模中间部位的外径为Dd。圆管的上端包裹住压模，且圆管的顶端设置8个预制切口，让劈裂变形更容易发生。图2为机构的有限元模型，压模和下板设置为刚体，下板固支，压模以2 m/s的速度轴向挤压薄壁圆管。薄壁圆管采用单元尺寸为1 mm的S4R单元划分，厚度方向上设置5个积分点，所有部件之间采用罚函数接触算法，摩擦因数取0.07。

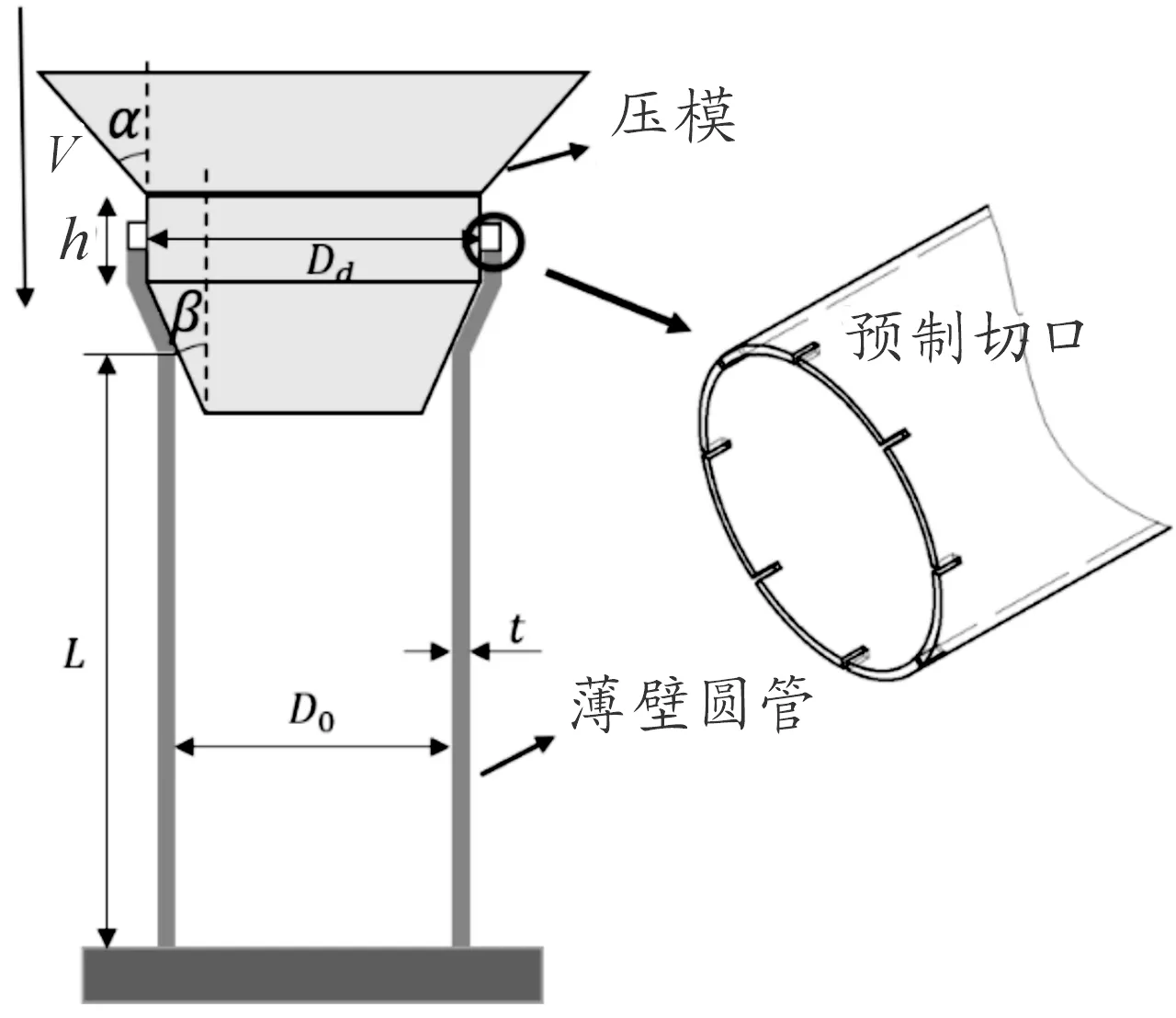
图1 膨胀-劈裂组合模式机构示意图

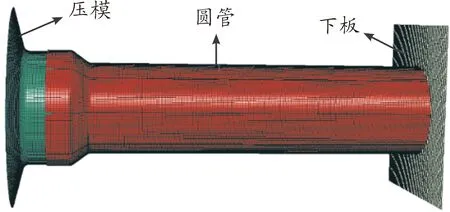
图2 有限元模型图

薄壁圆管材料选择为45#钢，弹性模量为210 GPa，泊松比为0.3，密度为7.8 g/cm3，其本构关系采用Johson-Cook模型，且暂不考虑应变率和温度效应：

σ=A+Bεn,εf=D1+D2exp(-D3σ*)

(4)

式中：σ等效应力；ε表示等效塑性应变；εf为失效应变；σ*为应力三轴度，是静水压力与Mises等效应力的比值；A、B、n、D1-D3为材料参数，如表1所示[13]。

表1 45#钢的力学参数

压模的上锥角α、下锥角β和压模外径Dd为3个设计变量，上锥角的参数变化范围为[45°,75°]，下锥角的参数变化范围为[5°,35°]，压模外径的参数变化范围为[56 mm,64 mm]。

2 试验设计

在建立响应面模型时，试验点的选取应遵从一定的准则，以便只取少量的点就能使近似函数达到较高的精度。本文采用的是中心复合设计方法，同时考虑试验点在设计参数空间中的正交性和旋转性。它的试验点数目N由3部分组成：

N=2p+2P+m0

(5)

其中：p为自变量的个数；2p代表的是因子设计点个数；2p代表的轴点个数；mo为中心点个数。N个试验点分布在设计参数空间3个半径不相等的球面上，其中因子设计点在半径ρ=1的球面上，轴点在半径ρ=γ的球面上，中心点在ρ=0的球面上。mo和γ的取值与设计变量个数p相关，以使得回归系数求解矩阵不退化。

2.1 编码转换

压模结构包含3个设计变量α、β、Dd，三变量对应下的γ=(2p)1/4=1.682，mo=6，即有N=20个试验点，图3展示了每一个试验点对应的编码坐标，及其在设计空间中的相对位置。将设计变量参数空间分为5个水平面，并将相关参数进行编码转换，如表2所示。

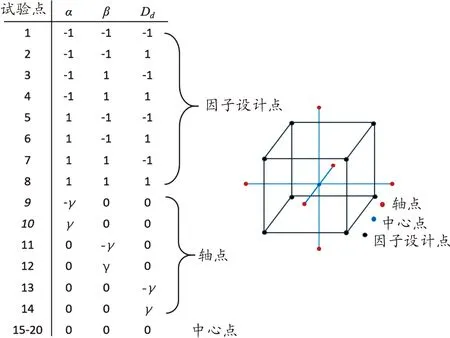
图3 试验点编码坐标及其在参数空间中的位置分布

表2 相关变量编码转换

2.2 试验设计结果

组合模式下圆管变形过程如图4所示，管壁在压模的挤压下，先发生膨胀变形，紧接着膨胀和劈裂两种变形同时发生。对应的载荷-行程曲线如图5所示，随着压模行程的增大，载荷迅速上升到第一个稳定阶段，这个阶段是由于圆管只发生膨胀变形造成的；当行程继续增大，管壁顶端与压模上锥角接触，管壁顶端也开始发生膨胀变形，此导致载荷又迅速上升；当圆管顶端膨胀到一定程度，顶端预制切口处的应变达到失效应变，管壁劈裂成八瓣，并在上锥角的约束下发生卷曲变形；此时，载荷迅速下降至第二个相对稳定的阶段，并围绕着一个稳定载荷呈周期性波动。试验设计的结果如表3所示，同时列出了相应的参数响应值。

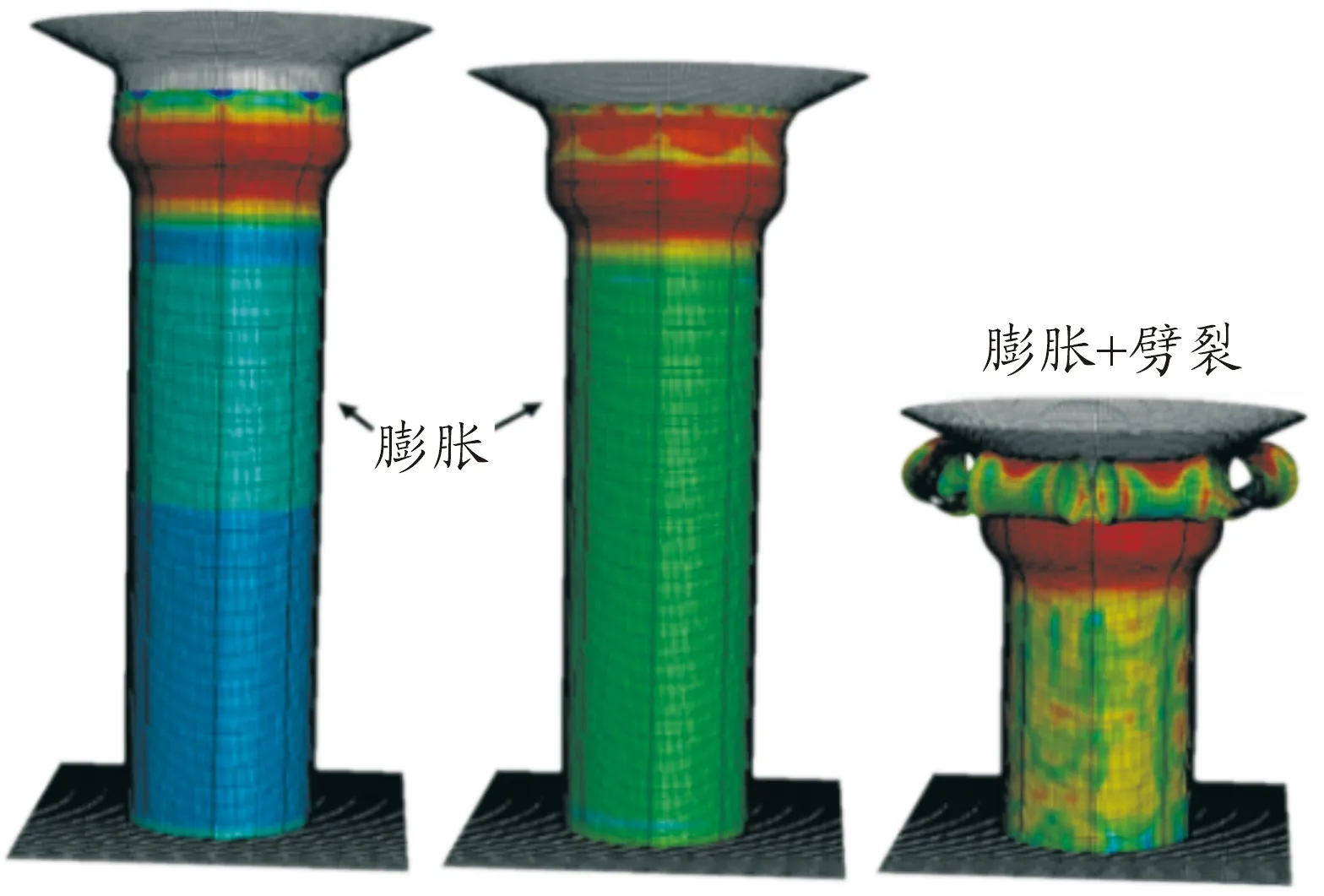
图4 薄壁圆管组合模式下的变形过程

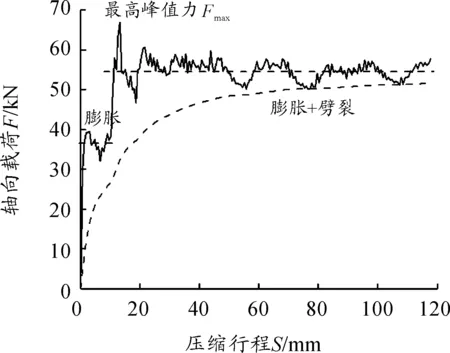
图5 薄壁圆管载荷-行程曲线

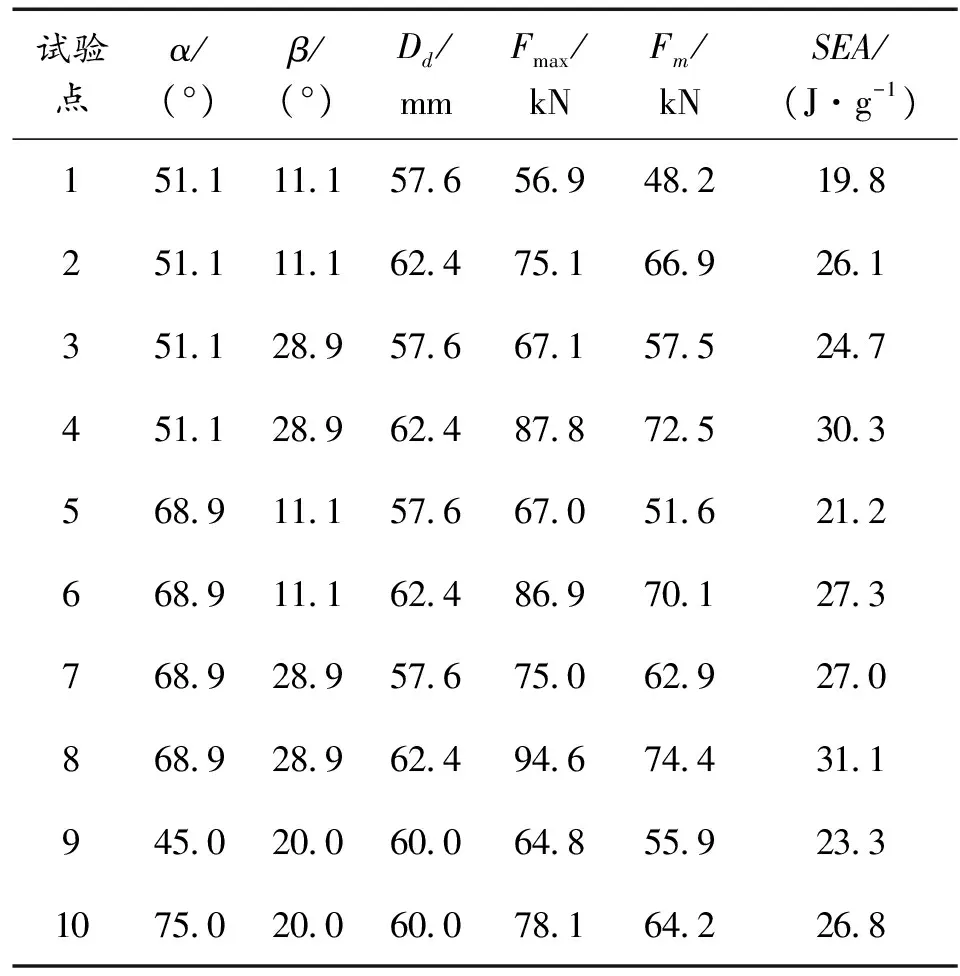
表3 试验点的吸能性能响应参数

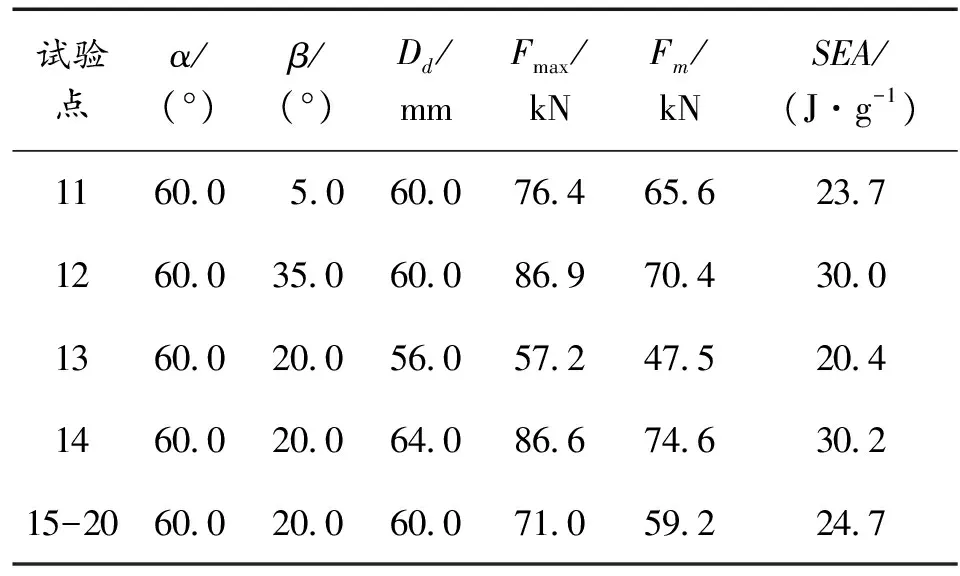
续表(表3)

3 响应面模型的建立

3.1 响应面模型回归系数的确定

由文献[2-4]可知，当摩擦因数大于零时，下锥角β对膨胀变形的载荷响应是非线性的，因此在这里采用二次多项式作为实际函数f(x)的近似函数，三变量下的二阶响应模型为：

(6)

式中，x1、x2、x3分别代表试验点在参数空间中的编码坐标值。

利用最小二乘法原理，使得近似函数与实际函数的误差最小，以来确定响应面函数的回归系数b，其计算公式为：

(7)

(8)

(9)

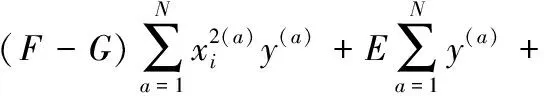
(10)

常数e、K、E、F、G与λ和p相关：

(11)

根据式(7)～式(11)，分别计算得到组合变形模式下平均载荷力Fm、最高峰值力Fmax和比能量吸收率SEA的二阶响应模型方程为:

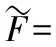
0.09x1x2-0.46x1x3-1.34x2x3+

(12)

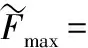
0.09x1x2-0.08x1x3-0.28x2x3+

(13)

0.06x1x2-0.21x1x3-0.34x2x3+

(14)

通过式(15)将x1、x2、x3转化成α、β、Dd，从而得到各吸能性能响应量与设计变量α、β、Dd之间的关系：

(15)

3.2 响应面模型的显著性和精度分析

上述所求响应面模型能否真正反映设计目标y与设计参数的统计规律性，或是否可以作为有意义的二阶近似模型，还需要对模型的显著性进行F检验，并通过复相关系数R2和相对平均绝对误差RAAE对响应面模性的精度进行评估：

(16)

(17)

(18)

由式(16)～式(18)对响应面模型的相关参数进行计算，如表4所示。查F临界值表，有F0.05(9，10)=4.92，三响应面模型的吸能F值都大于4.92，说明三响应面方程都是高度显著的。响应面模型的R2都较高，分别是0.99、0.98；且RAAE都较小，分别是0.009、 0.012和0.015，说明三响应面模型对实际函数的逼近程度很好，模型精度较高。

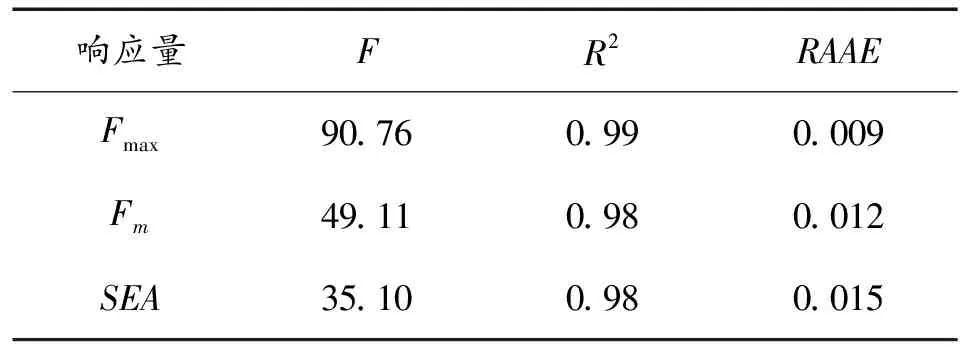
表4 响应面模型的显著性和精度参数

4 讨论

4.1 压模结构参数对吸能性能参数的影响

图6和图7分别为平均载荷力和最高峰值力的响应曲面，可看出两载荷响应量与各设计变量的关系大致相似；两载荷响应量与上锥角和压模外径呈单调递增的关系，但会随着下锥角的增大先增大后减小。当下锥角的角度在10°～15°时，载荷会存在最小值。文献[2-4]指出当摩擦因数大于0时，膨胀管压缩载荷与压模锥角之间也有类似的关系，因此组合变形模式下该现象的发生应为摩擦力的存在对膨胀阶段产生影响而造成的。

图8为比能量吸收量的响应曲面，圆管在组合变形模式下，其比能量吸收量随着上下锥角和压模外径的增大而增大。结合图1和6，可看出下锥角在小角度下，平均载荷较大，在相同的行程下吸能量较多；但其角度越小，圆管上端需要包裹压模的部位就越多，相同的压模行程下，薄壁圆管有效变形区域的质量就会越大，从而导致比能量吸收率与载荷在下锥角小角度下呈现较大差异的原因。结合式(3)、式(11)、式(12)可做出结构吸能效率的响应曲面(图9所示)，可看出组合变形模式下薄壁圆管的吸能效率在0.76～0.92之间，上锥角越小，吸能效率越高。

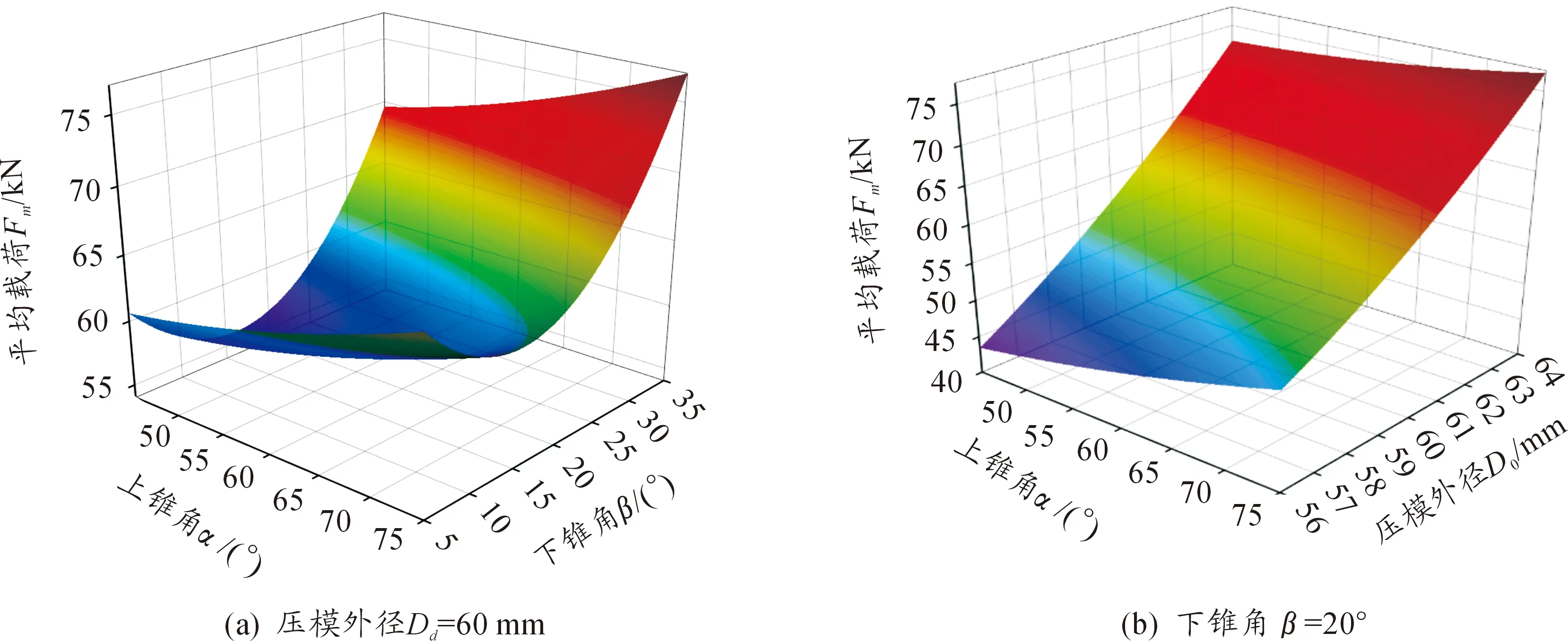
图6 平均载荷力响应曲面

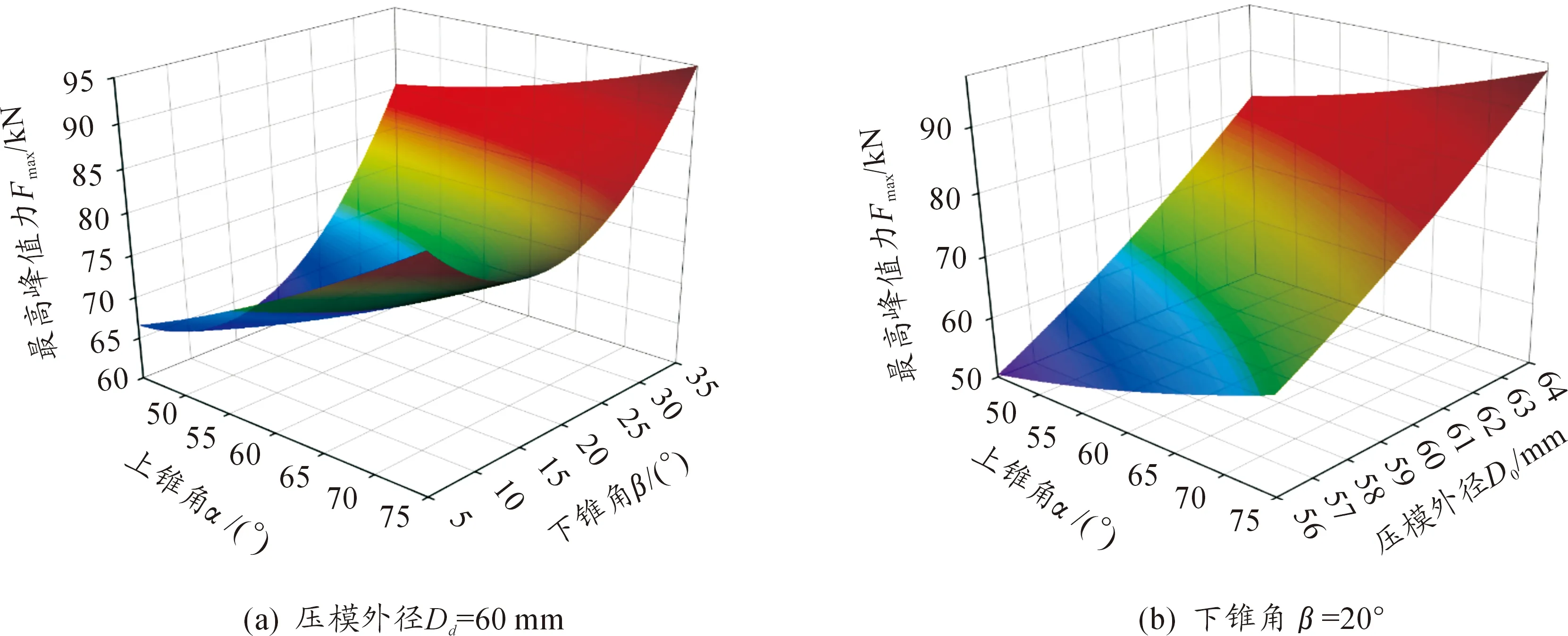
图7 最高峰值力响应曲面

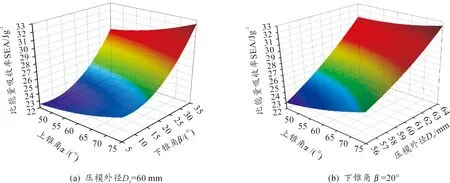
图8 比能量吸收率响应曲面

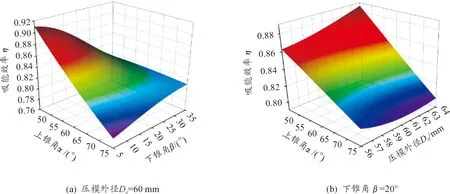
图9 吸能效率响应曲面

4.2 结构优化

对于吸能结构，所希望结构的比能量吸收率要尽量大，且其最高峰值力要尽量小。对两者同时考虑，即进行多目标优化，其数学表达式为：

(19)

为得到同时考虑两个性能指标的优化结果，采用非域分类遗传算法(NSGA-II)，做出两指标之间的Pareto前沿面，如图10所示。可看出，两者呈现正相关的联系，即存在很强的竞争关系。因此，如果设计者更注重结构的比能量吸收率，就要考虑右上角的解，这同时意味着较高的峰值力，反之亦然。单方面侧重的优化结果，如表5和表6所示。传统上，最令人满意的决策通常是由权重法来决定的，它将所有的目标集合成于加权平均相关的单个成本函数，以强调它们的相对重要性。然而，在实际工程应用中，很难为每个目标分配适当的权重。为了从Pareto前沿面中确定最满意的解，可通过理想点法确定最优点，其数学表达式为：

(20)

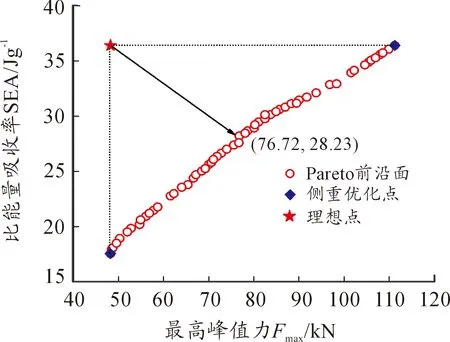
图10 Pareto前沿面

表5 侧重比能量吸收率的优化结果

表6 侧重最小峰值力的优化结果

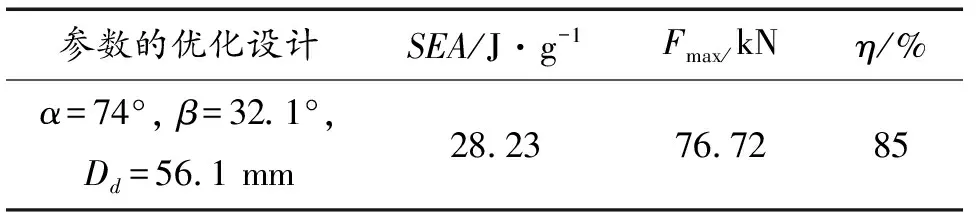
表7 理想点法优化结果

已有文献[8-10]指出，该组合变形模式能提高其对应单一变形模式下薄壁圆管圆管的吸能性能。但是针对薄壁圆管在该组合变形模式和渐进压溃变形模式下的吸能性能比较，还未有文献指出。对相同几何尺寸的薄壁圆管进行渐进压溃的数值计算，其有限元模型及仿真结果如图11所示，表8列出渐进压溃变形模式下薄壁圆管的吸能性能参数。结合表5和表7看出，相对渐进压溃变形模式，当压模的几何参数为α=75°、β=35°、Dd=64 mm时，组合变形模式下的比能量吸收率提高了1.4倍，其最高峰值力减弱了21%；当压模的几何参数为α=74°、β=32.1°、Dd=56.1 mm时，组合变形模式下的比能量吸收率提高1.1倍，其最高峰值力减弱了45%；且在不同几何结构的压模下，薄壁圆管在组合变形模式下的吸能效率大于70%，而渐进压溃变形模式下的吸能效率为46%，组合变形模式下圆管的吸能过程更加平稳。因此，可以看出该组合变形模式在一定的压模结构设计下，其吸能性能优于渐进压溃变形模式，且其载荷响应能通过压模结构调节以适应不同的工作环境。

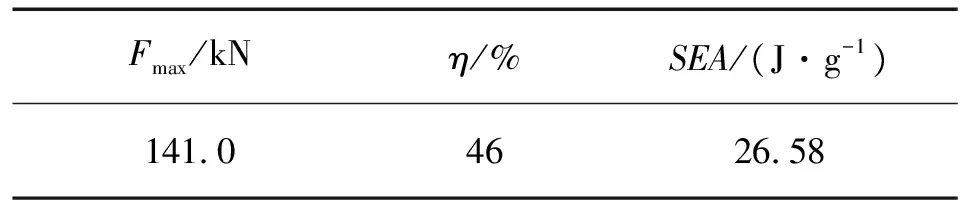
表8 薄壁圆管渐进压溃变形模式下的吸能性能参数

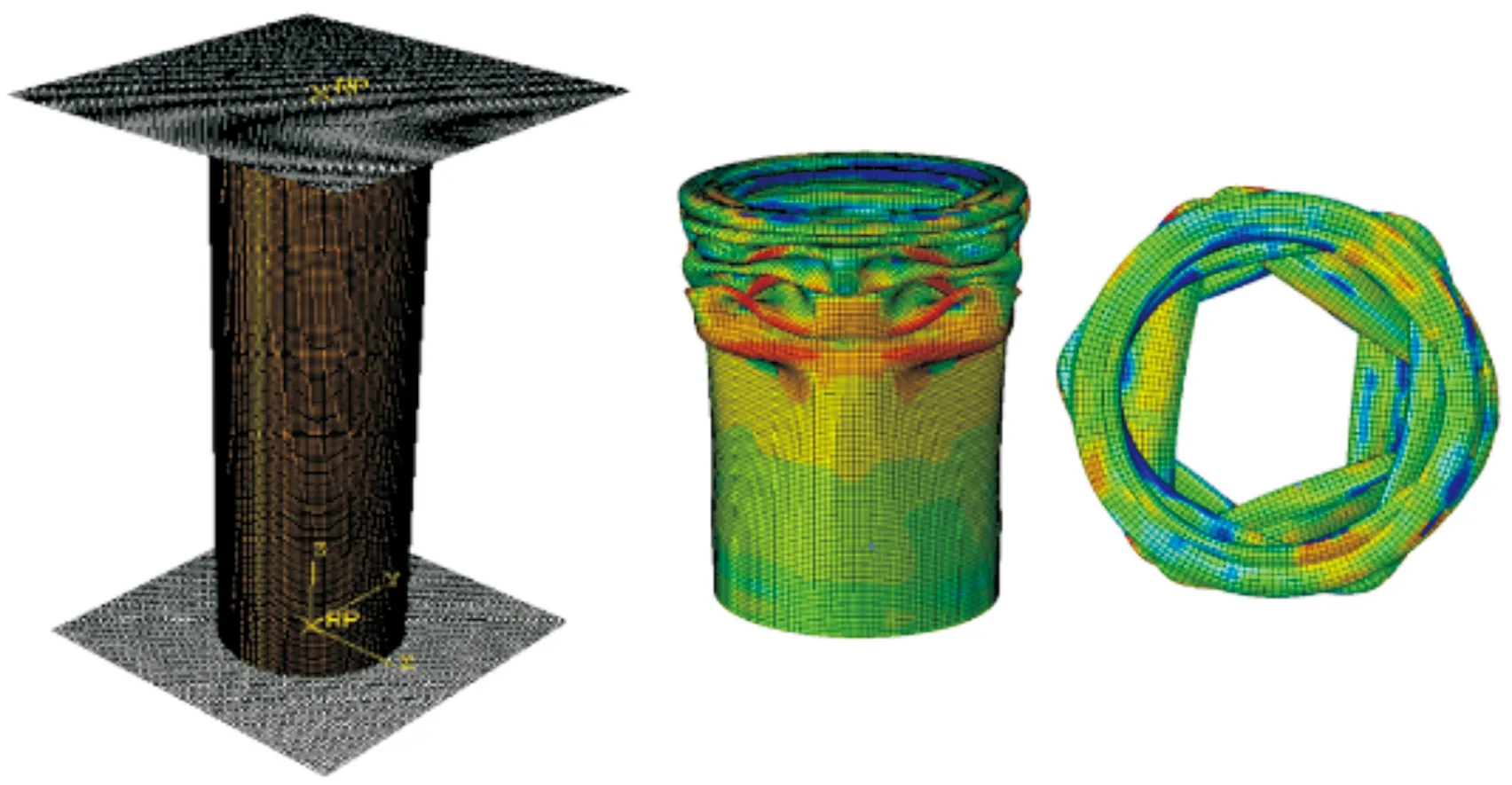
图11 有限元模型及变形结果

5 结论

1) 在组合变形模式下，薄壁圆管的载荷响应量随着上锥角和压模外径的增大而增大，随着下锥角的增大先增大后减小。吸能效率在76%～92%，随着上锥角的增大而减小。

2) 在组合变形模式下，薄壁圆管的比能量吸收率随着上锥角、下锥角和压模外径的增大而增大。

3) 相比较于渐进压溃变形模式，当以比能量吸收率最大为优化目标时，组合变形模式下薄壁圆管的比能量吸收率提高1.4倍，最高峰值力减弱21%；当以多目标优化为目标时，组合变形模式下的比能量吸收提高1.1倍，最高峰值力减弱45%。