预控破片战斗部的成型与散布分析

赵 进,付建平,陈智刚,郭子云,张 钧,郑灿杰

(1.中北大学 机电工程学院， 太原 030051； 2.中北大学 地下目标毁伤技术国防重点学科实验室， 太原 030051；3.晋西工业集团有限公司防务装备研究院， 太原 030041； 4.山东特种工业集团， 山东 淄博 255200)

预控破片又称为半预制破片，破片的大小与外形是利用专门的技术处理，如壳体内、外表面刻槽、材料区域脆化等控制或引导壳体的断裂[1]。最常见的预控破片战斗部是利用预刻槽手段，即在壳体内壁或外壁上事先刻有规则交错的沟槽，将战斗部壳体划分为破片集合。当战斗部壳体受到炸药爆轰产物的作用时，应力集中会在其预刻槽根部产生，并在此处沿特定走向的轨迹断裂，破片的形状、尺寸和数目由刻槽参数及分布决定[2-3]。预控破片战斗部因其能生成质量均匀、数量众多的破片，且破片形状可根据需要进行设计，因而具有很好的应用前景,现已成为国内外很多学者研究的热点。郭策安等利用数值模拟的方法得到了内刻V形槽预控破片战斗部刻槽参数对壳体断裂形成有效破片数量的影响，并通过爆坑试验回收破片，与仿真结果基本一致[4]。吴成等利用理论计算与实验对比的方法，得出内刻V形槽战斗部壳体的临界断应变判据，并通过试验验证了断裂判据的正确性[5]。张高峰等通过使用理论分析和试验验证的方法论证了对称刻槽预控破片战斗部壳体在爆炸过程中周向与轴向的质量损失率[6]。刘桂峰等研究了刻槽参数对壳体断裂形成破片形成的影响，同时对外刻槽式预控破片战斗部壳体模型进行了简化[7]。通过上述研究可以看出，数值模拟计算成为了学者进行设计研究的一项重要技能，LS-DYNA有限元软件已成为战斗部设计和优化的一种重要工具。

目前关于预控破片的研究在壳体外刻槽和刻槽参数的选择方面较多，但是关于内刻槽预控破片形状对壳体断裂成型的对比上研究较少。本文基于LS-DYNA有限元软件，对菱形破片战斗部和矩形破片战斗部的壳体断裂过程进行了数值模拟和分析研究，比较了两种战斗部破片的成型情况和散布，选择出合理的破片形式，最终通过壳体破碎试验验证了仿真和理论计算的准确性。

1 物理模型及计算方案

1.1 物理模型

预控破片战斗部破片的形状由壳体上刻槽网格的形态决定，采用相同的圆柱形壳体，在壳体内刻以一定走向的V形槽， 其中h1为刻槽深度，θ为刻槽角度，如图1(a)所示。菱形破片网格角选用60°时可获得最佳壳体破碎[8]，为保证壳体的完整性，壳体顶部与底部由完整菱形的一半排列而成，其余全部是由完整菱形构成，其槽走向为60°，槽与槽的相交处夹角同样为60°，其中完整菱形破片有960个，半菱形破片有80个，如图1(b)所示,单个菱形破片尺寸如图1(d)所示。矩形破片网格角为90°，周向与轴向槽相互垂直，破片总数为800个如图1(c)所示，单个矩形破片尺寸如图1(e)所示。

1.2 仿真模型及材料参数

LS-DYNA软件是进行仿真计算的一种重要工具。考虑有限元模型的多材料复杂过程的相互作用，模拟了壳体膨胀破碎过程。为采集战斗部壳体上每个预制破片质心点的多种矢量，采用拉格朗日算法，战斗部装药及空气采用任意拉格朗日欧拉(ALE)算法，网格间物质可以相互流动。TrueGrid前处理软件可以用来构建和划分复杂实体的网格，因此战斗部网格模型由其构建，为保证战斗部壳体上V形槽断裂与实际相符，网格划分时刻槽处网格要保证细致均匀，全模型建模计算机处理会非常慢，采用1/4模型计算，在1/4模型的对称面上设置对称约束条件。所有计算网格均采用六面体实体单元，起爆方式是顶端中心单点起爆，建立模型时以起爆点为坐标原点，起爆点以下沿弹轴方向为z轴的负方向，图2为两种战斗部壳体的有限元模型，左侧延伸至壳体y正方向，右侧延伸至壳体为x正方向。

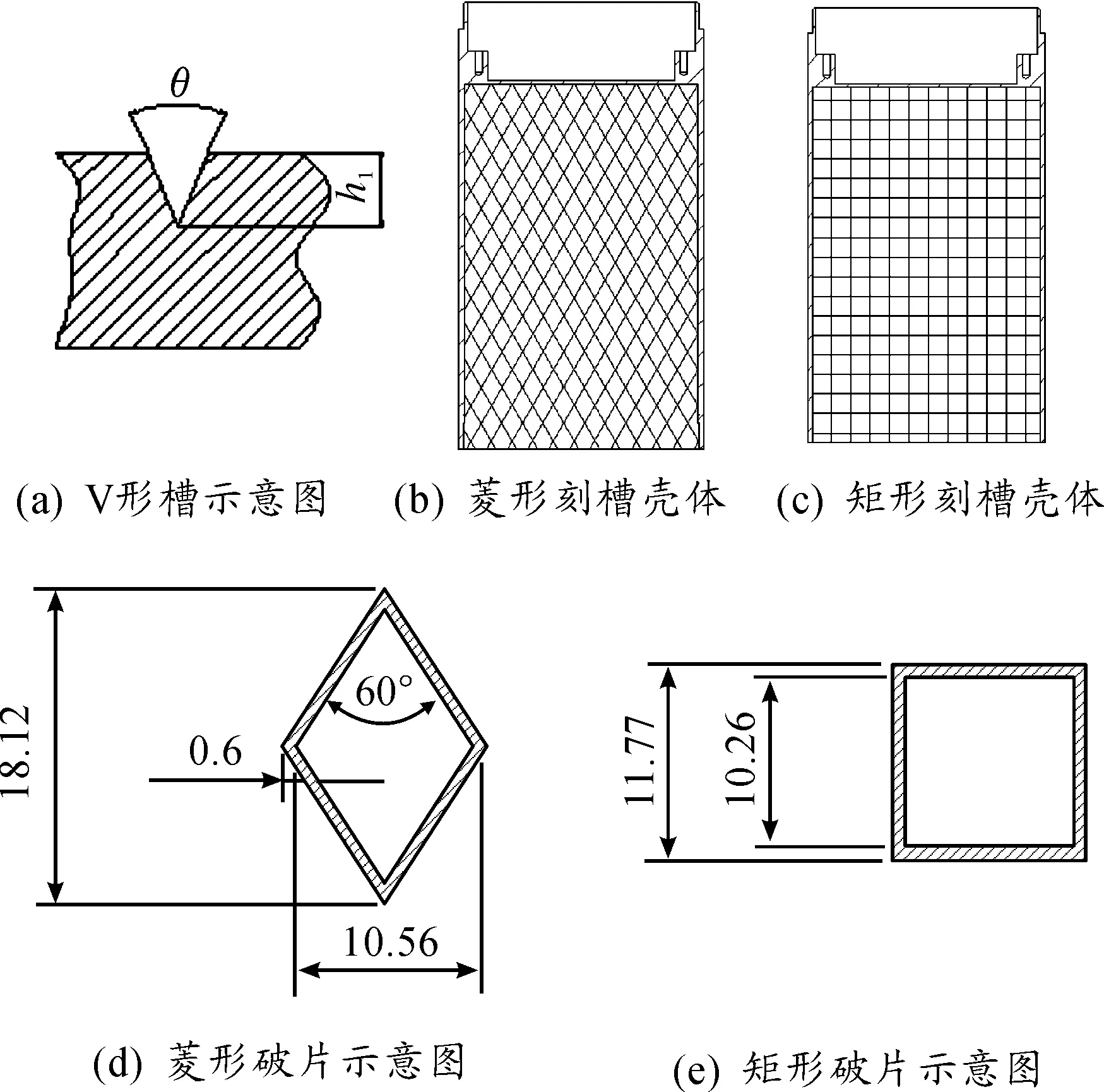
图1 战斗部壳体结构示意图

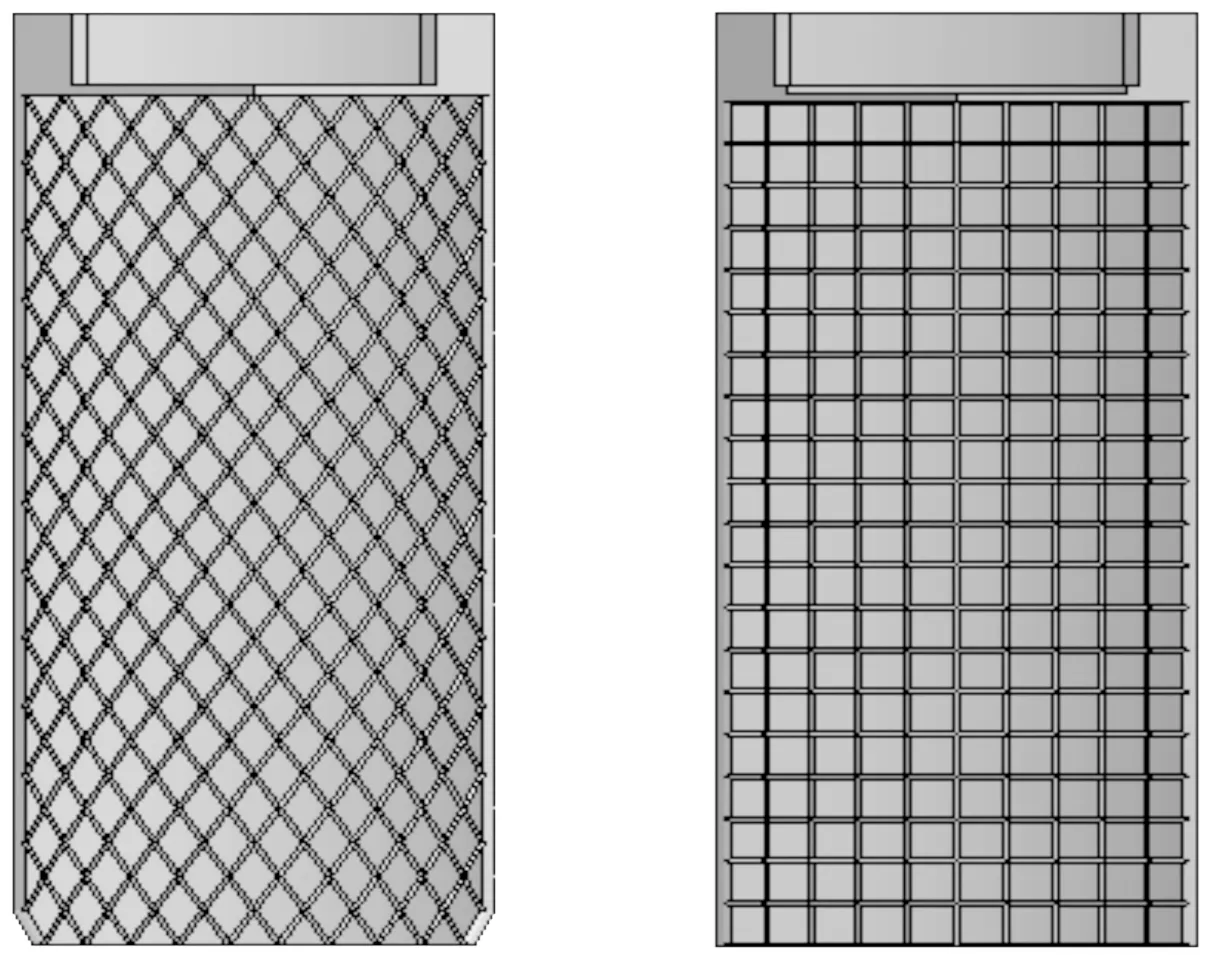
图2 战斗部壳体有限元模型

战斗部壳体材料为45#钢，用运动强化和等向塑性的金属材料的PLASTIC_KINEMATIC模型描述。部分参数取值见表1。

表1 壳体材料PLASTIC_KINEMATIC模型参数

战斗部炸药为8701炸药，由于HIGH_EXPLOSI VE_BURN模型使用惠更斯原理和C-J理论来定义爆轰速度和炸药能量释放的位置，即爆轰波以C-J爆轰速度向各个方向传播。炸药爆轰产物的膨胀过程的理想状态用JWL状态方程描述，因此，计算模型中炸药选用JWL状态方程和HIGH_EXPLOSIVE_BURN模型来描述。部分参数取值为：ρ=1.73 g/cm3,D=8.5 km/s,pCJ=29.8 GPa。部分参数取值见表2。

表2 8701炸药JWL状态方程参数

空气用NULL模型和LINEAR_POLYNOMIAL状态方程一同描述。

1.3 破片散布计算公式

战斗部壳体在爆轰产物作用破碎后形成破片，根据数值仿真结果得到破片质心的各种矢量，可以通过这些矢量运算。

此处仅需要计算破片在x-y平面内的破片飞散的角度，根据Shapiro公式[8]，将破片矢量代入得到破片抛射角公式：

θ=arc tan(vy/vx)(180/π)

(1)

式中：θ为破片飞散角，vx为破片在x方向上的分速度，vy为破片在y方向上的分速度。

根据破片在x方向和y方向的分位移和分速度，计算出破片飞行时间，再通过破片z方向的分速度得到破片飞行高度，计算公式如下：

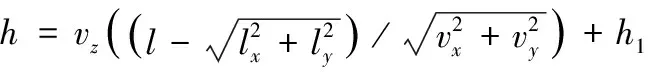
(2)

式中：vz为破片在z方向上的分速度，l为破片距离圆心的距离，lx为破片在x方向上的位移，ly为破片在y方向上的位移，h1为炸药设置起爆点到原点的距离。

2 结果分析

2.1 壳体断裂过程分析

为对比两种战斗部壳体断裂形成破片的过程，特选取了壳体破碎的3个典型时刻，如图3所示。在t=30 μs时，当爆轰产物持续不断的作用于壳体时，在壳体刻槽根部会引起应力集中，菱形破片战斗部壳体直径膨胀达到1.74倍弹径时，则开始沿着预刻槽位置发生断裂，矩形破片战斗部壳体仅需膨胀到1.59倍时就可以发生断裂；在t=45 μs时，爆轰产物在受到壳体周向的约束力时，开始沿着轴向方向向下传播，断裂开始沿轴向向下扩散；当t=60 μs时，壳体完全断裂形成破片。

由图3可以看出两种战斗部壳体断裂在形成破片时，最主要的区别是菱形破片战斗部壳体可以完全断裂形成单个破片，矩形破片战斗部仅可以沿周向预刻槽位置发生断裂，形成条状连片。两种战斗部壳体断裂时都是从壳顶周向第一排和第二排预刻槽交叉点处率先开始断裂，但由于预刻槽交叉的角度和壳体周向、轴向膨胀速率的不同，菱形破片战斗部壳体总是在轴向两排的预刻槽交叉点处开始断裂，再沿预刻槽扩散，如图4所示；矩形破片战斗部在预刻槽交叉点处发生断裂后，轴向预刻槽处产生的应力不足以使破片断开，会迅速沿着周向方向下传播，如图5所示。

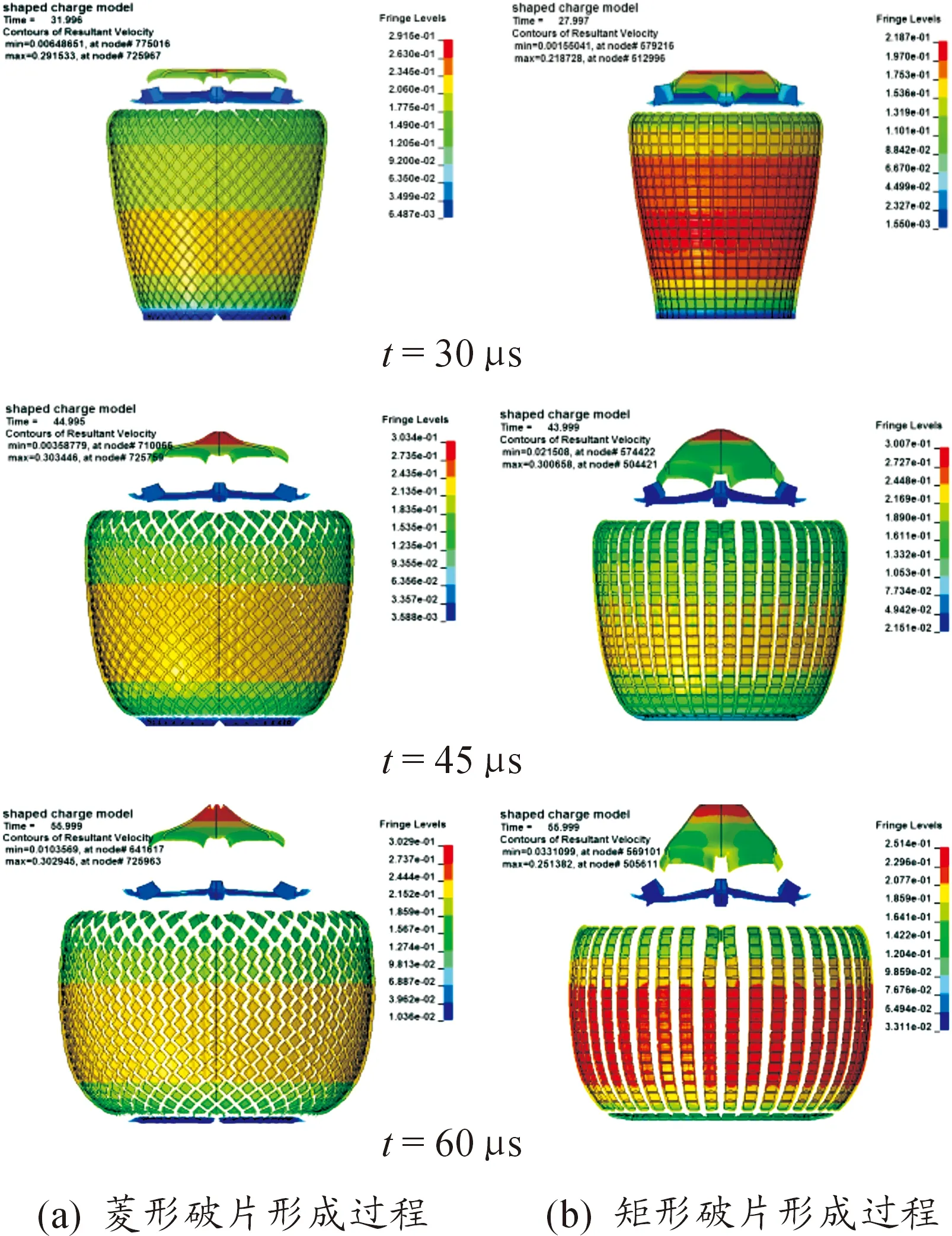
图3 战斗部壳体断裂过程

图4 菱形破片战斗部壳体断裂形式

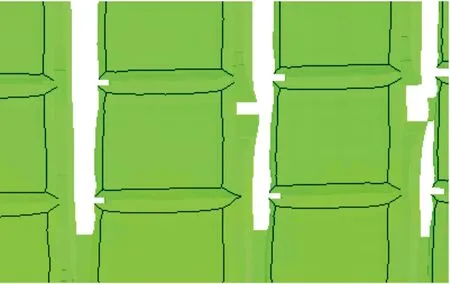
图5 矩形破片战斗部壳体断裂形式

2.2 破片散布分析

在数值建模时，采用质心点追踪法追踪每一个破片的质心点，根据数值模拟结果可以获知每一个破片质心点的各种矢量，以此代替破片的各种矢量，再利用式(1)和式(2)计算出破片在7m处距离地面的高度和飞散角，再绘制出破片在7 m处的散布图。

由图6可知，菱形破片战斗部壳体断裂情况极佳，破片分散在距离地面0.25 m到1.65 m之间，破片连片数很少，单个有效破片数量多，覆盖范围广，其分布呈条状，单条上有11到12个破片。矩形破片战斗部由于壳体断裂情况不佳，轴向连片严重，破片分布集中在1.25 m到1.75 m之间，散布范围集中有限且很不规则，单个有效破片数量少，分布明显不如菱形破片战斗部，如图7所示。

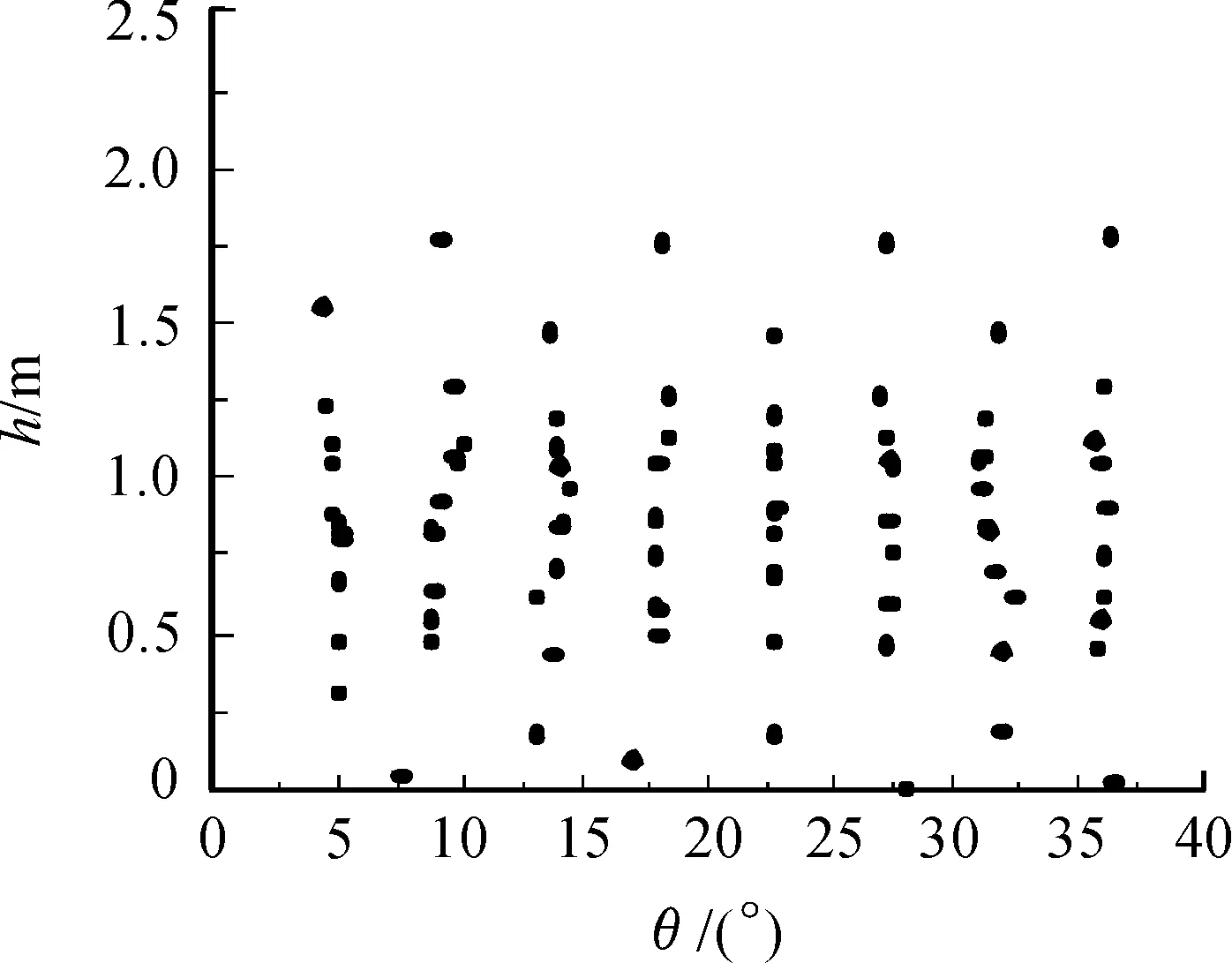
图6 菱形破片预测散布

图7 矩形破片预测散布

3 验证

张高峰等[6]在研究对称刻槽预控破片战斗部壳体爆炸过程质量损失率时，做过壳体内周向和轴向均刻有V形槽战斗部的水井静爆试验，根据其破片回收的图片可以看出，矩形破片战斗部在断裂形成破片时，破片有明显的连片。

菱形破片战斗部壳体采用45#钢制成，如图8，静爆试验时战斗部爆心距离地面为1.5 m，战斗部底朝下，顶端雷管起爆，单块Q235钢靶宽1.5 m、高2 m、厚8 mm，试验时靶板由4块钢靶扇形排布，距离战斗部7 m，为方便统计破片散布情况，在每块钢靶上都画有长200 mm、宽200 mm的方格，有一侧边界是长100 mm、宽200 mm的长方形网格，试验布置如图9：

图8 战斗部壳体

图9 试验布置

试验结束后破片侵彻靶板后的典型照片如图10，由靶板图可以看出，菱形破片在飞行时虽然受到环境(风向、风速等)影响，但基本呈条状排布，且菱形破片列与列之间是错位排布，相邻两条破片有一定落差，单条上平均分布有12个破片，上靶率为92%，而且破片全部可以贯穿靶板，且只有一处连片。

图10 菱形破片战斗部试验后靶板照片

根据试验结果将破片的实际着靶位置绘制成破片散布图，如图11所示，可以看出其在四块靶板上分布比较均匀，上靶破片总数为108个，与数值模拟和计算的结果相吻合。

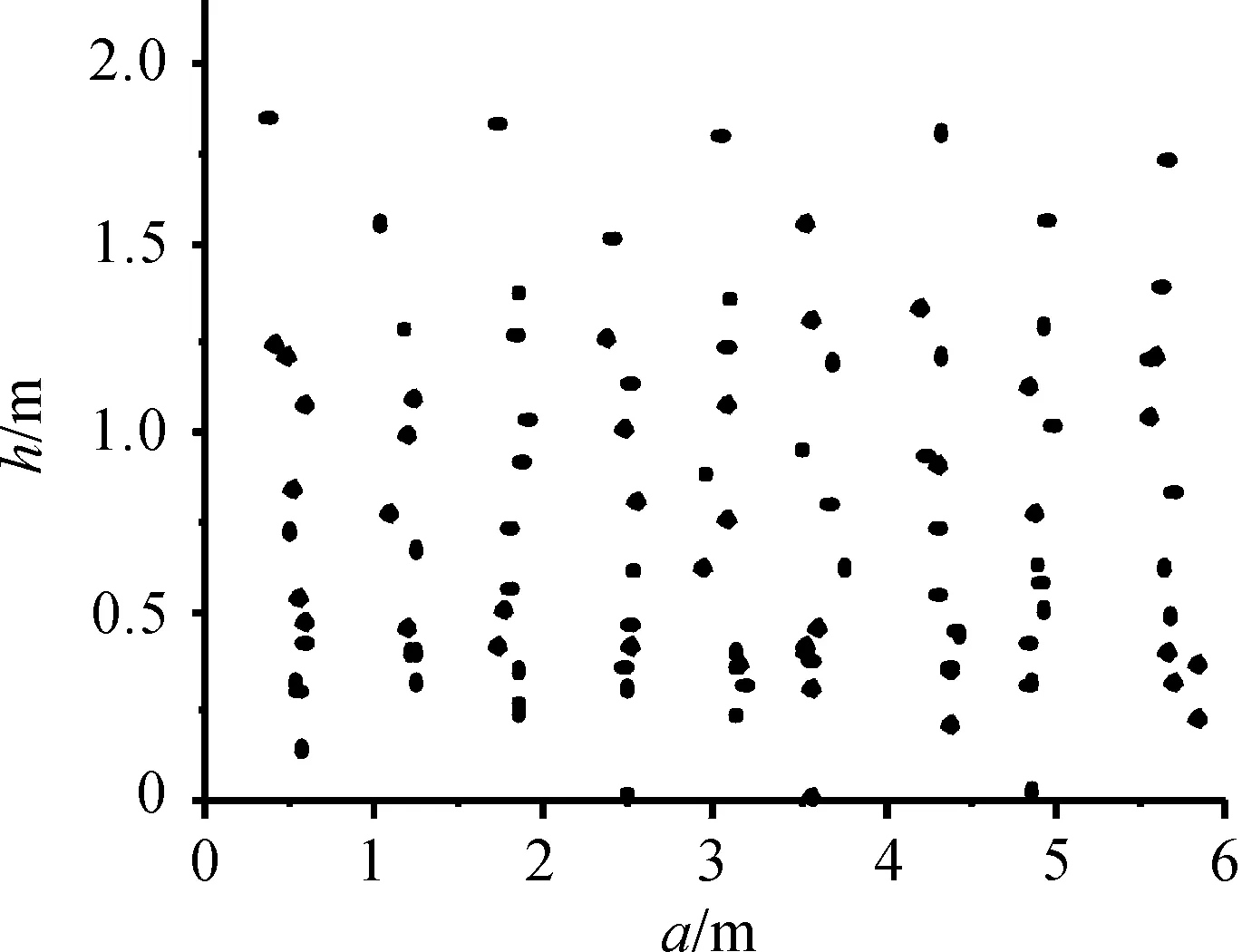
图11 菱形破片实际散布

4 结论

1) 通过数值模拟对比菱形破片战斗部与矩形破片战斗部壳体断裂成型过程，矩形破片战斗部在轴向断裂情况不佳，形成条状连片，菱形破片战斗部壳体破碎率高，破片成型效果好，连片率低；

2) 矩形破片战斗部壳体断裂时，从轴向两排的预刻槽交叉点处开始断裂，沿周向预刻槽位置向下传播，菱形破片战斗部壳体破裂时，断裂也是从轴向两排的预刻槽交叉点处开始断裂，再沿预刻槽扩散，形成单个破片；

3) 矩形破片战斗部散布范围有限，覆盖面积小且不规则，菱形破片战斗部破片散布均匀，单列菱形破片基本呈条状分布，上靶率高，通过静爆试验验证菱形破片战斗部散布规律，与仿真计算结果相吻合。