基于复杂网络的社区发现算法研究
孟彩霞,李楠楠,张 琰
(西安邮电大学 计算机学院,陕西 西安 700121)
0 引 言
在现实世界中存在各种复杂系统,这些系统通常可以以网络的形式表达,比如常见的电力网络、航空网络以及社交网络等复杂网络。复杂网络具有小世界、无标度、社区结构等许多基本特性,而其中最为重要的特性是社区结构。为了挖掘这些社区结构,可以使用一些不同领域的方法,如数据挖掘中的聚类或图论中的图分区等,挖掘社区结构的过程统称为社区发现[1]。通常将网络表示为图,图中的点表示网络中具体的实体,边表示网络中实体与实体之间的关联[2-3]。大多数关于社区检测的论文使用图作为网络的数学表示,更精确地说是无向图。然而,很多真实网络具有复杂的关系,并且都是有权值和方向的。此外,将有向图转化为无向图会导致信息的丢失,从而使检测到的社区结构没有真正意义[4]。由于很少有文献提出在有向网络中进行社区检测,因此对有向有权的复杂网络进行社区发现是一项艰巨而有意义的任务[5]。
2007年,Raghavan等[6]提出了一种标签传播算法(LPA),该算法是一种近似线性复杂度的社区发现算法,并且不需要预先知道社区的规模大小和所需要划分的社区个数等,因此受到学者们的广泛关注和应用。但LPA在标签传播过程中存在随机性、振荡、不稳定,划分社区效果差等缺点,为此大量研究人员进行了相关研究。Sun等[7]提出了一种基于α-degree邻域影响的标签传播算法,缓解了节点更新中随机更新的问题,提高了算法的稳定性。Yan Xing等[8]提出了KBLPA和NIBLPA算法,该算法以K-shell算法为依据分析节点的重要性。易秀双等[9]提出了一种基于顶点影响的局部社区发现算法,提高了算法的计算速度和效率。黄佳鑫等[10]在标签传播的思想上综合考虑了节点的重要性和标签的影响力,因此提高了原始标签传播算法的稳定性和准确性。彭磊等[11]依据节点相似度进行更新,提出了NSLPA算法。许合利等[12]提出了一种基于核心节点的加权网络中的局部检测算法CRD-LPA。但是以上这些算法大多数是基于无向图的,因此失去了一些有用的信息,只对社区检测结果进行定量分析。
文中考虑边的方向和权值,将标签传播思想应用于有向加权网络,并且通过加权的ClusterRank获得节点重要性列表,以避免LPA中的随机选择。其次,采用Jaccard系数度量节点的相似度,结合节点重要性列表计算出一个新的度量CRJ(重要度和相似度),提高算法的稳定性和社区发现质量。
1 标签传播算法
标签传播算法是一种接近线性复杂度的社区发现算法,其基本思想是用已知节点标签信息预测未知节点的标签。
具体算法描述如下:
(1)将所有节点的标签初始化为唯一值,例如初始化节点标签为其ID号。
(2)随机地对图中的所有节点进行排序。
(3)根据步骤2按顺序更新每个节点,将节点的标签更新为邻居中出现次数最多的标签;若当个数最多的标签不唯一时,随机选一个标签赋给当前节点。
(4)如果网络中的所有节点的标签均稳定不变,则算法终止。否则,返回步骤2继续。
基于标签传播算法的社区检测的具体过程如图1所示。
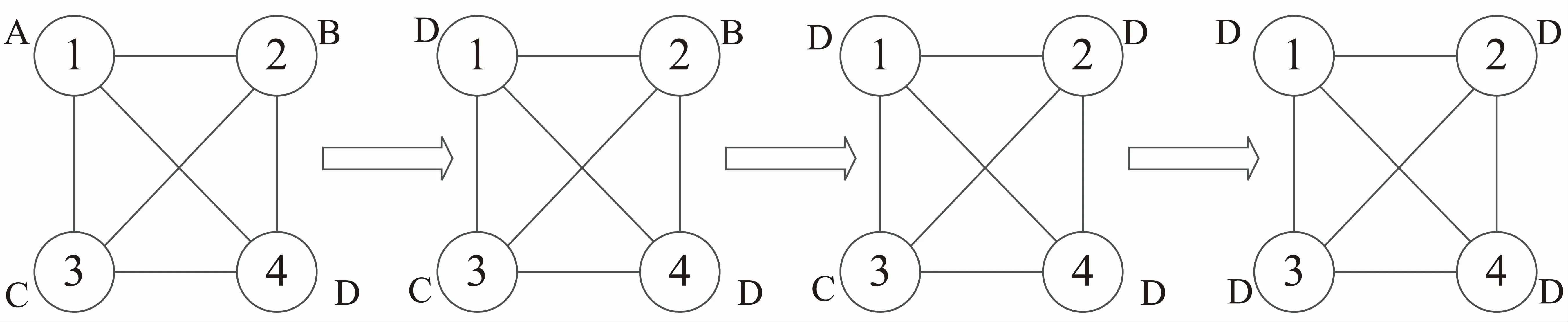
图1 基于LPA的标签传播过程
在图1中有四个节点,每个节点ID为1,2,3,4,它们的标签被初始化为A,B,C和D。
在标签传播过程中,节点1的标签随机选择为节点4的标签D后,与节点2相邻的节点中,标签D的数量最多,因此节点2的标签也设置为D,这样的过程不断持续下去,直到所有可能聚集到一起的节点都具有了相同的社区标签,此时图1中所有节点的标签都变成了D,所有节点都已达到算法的终止然后退出循环。
标签的更新策略分为:同步更新和异步更新。同步更新是指对于节点x,在第t代时,根据其邻居在t-1代时的社区标签进行更新。异步更新是指节点x,在第t代时,根据其邻居最新的社区标签进行更新。同步更新标签的方法对于二分或者近似二分的网络来说,可能会导致标签的振荡,所以选择异步更新节点标签的方式。
LPA算法的随机性有以下两个方面的问题:
(1)节点更新顺序的随机性。每次迭代开始时,都需要重新随机生成节点更新的顺序。但是,这种随机性的方法不仅可以产生最佳值,也可能会产生最差值,因此,增加了算法的不稳定性。
(2)当个数最多的标签不唯一时,标签选择是随机的。这种随机性可能会使得算法的迭代次数增加,并且导致算法不稳定,划分出来的结果也会相对较差。
针对第1个问题,提出基于加权的ClusterRank算法获得节点重要性列表来依次更新节点,避免随机选择;针对第2个问题,采用Jaccard系数度量节点的相似度,结合节点重要性列表计算出一个新的度量CRJ(重要度和相似度),选择度量值最高的标签进行更新,提高算法的稳定性和社区发现质量。
2 CRJ-LPA:改进的标签传播算法
LPA的效率吸引了众多学者和研究人员的关注和研究。有很多算法可以改善LPA的上述问题。NSLPA算法最大改进之处在随机选择。如果有多个可选标签,则节点将选择相似度的邻居节点的标签,而不是随机选择。此方法在一定程度上避免了LPA的随机性问题,
但仍存在逆流问题。CRD-LPA算法将ClusterRank系数与节点局部密度(local density of node,LDN)结合起来进行节点更新。此方法提高了LPA的准确性和稳定性,但CRD函数降低了节点影响力相同的概率,仍存在随机选择的可能性,同时该算法也忽略了节点边的方向性对结果的影响。
2.1 加权的ClusterRank算法
Chen等[13]根据节点的度和聚类系数对有向复杂网络的节点重要性进行了分析,并以此为基础提出了ClusterRank算法。该算法在考虑节点的邻居节点的数量的同时,还考虑到聚类系数对网络中信息传播的巨大影响。ClusterRank算法是对LeaderRank和PageRank算法做了进一步的优化和改进[14],但是ClusterRank没有考虑网络中节点周围的结构信息和边的权值,因此,无法有效地衡量有向加权网络中节点的重要性。考虑到这个问题,文中结合含权网络中节点强度的定义提出了基于加权的ClusterRank算法。
2.1.1 含权网络中的节点强度

(1)
(2)

上面定义的缺点很明显,忽视了节点的度,在网络中往往存在节点的邻居多而节点强度却很小的情况。Garas等[15]提出了另一种节点强度的定义方式,即用节点的邻居数量和边权重共同表示节点的度值,更加细致地刻画了节点的属性。在这里,节点vi的强度为:
(3)
其中,ki为节点vi的度;wij为节点vi与其邻居vj之间连边的权值;α和β为自由参数,用来调节度和权值之间的比重。
2.1.2 含权的局部聚类系数
许多社交网络把有向网络从i到j的连接表示为j是i的追随者,意味着j从i接收信息。将Γi表示为i的追随者集合,即i的出边集合,并且i的追随者之间的相互作用密度可以用i的局部聚类系数表示。有向网络的聚类系数定义为:
(4)
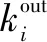
现有研究提出了计算适用于有向网络和加权网络的局部聚类系数的方法,但这些并不适用于加权定向网络。考虑到这一点,文中融合Garas等提出的节点强度概念和信息传播的因素,定义了加权定向网络上的局部聚类系数,如下所示:
(5)


2.1.3 含权的ClusterRank算法
对于ClusterRank只考虑节点的聚类系数,不适用于加权网络的问题,提出了适用于加权定向网络的ClusterRank算法。根据式5定义的加权定向网络上的局部聚类系数,重新定义了节点vi的ClusterRank的评分si:
(6)
s.t.f(ci)=10-ci
其中,Γι是节点vi的邻居节点集合;wij是节点vi与节点vj直接相连的边的权值;f(ci)是节点vi的聚类系数的函数。
在复杂网络中,聚类系数越大,越会阻碍信息的传播,因此随着ci增大的f(ci)值将变小。
2.2 Jaccard相似度
在复杂网络中,节点之间通常具有一定的相似性,Jaccard为描述相似度的重要指标。在包含节点集V和边集E的图G(V,E)中,节点vi和节点vj之间的Jaccard相似度定义如下:
(7)
其中,Ni表示节点vi的邻居节点的集合,Jaccard的值介于0~1之间,该值越接近1,表示节点vi和节点vj之间的相似度越高。
在LPA算法中,即使通过文中提出的基于加权的ClusterRank算法进行节点重要性排序后进行标签的更新,仍然有可能会出现一定的随机选择。因此,定义了一种新的度量CRJ,通过综合考虑节点重要性和相似性来提高LPA算法的准确性,定义如下:
(8)

2.3 CRJ-LPA算法描述
针对有向加权网络,基于原始的LPA算法,文中提出了一种基于节点重要性和相似性的改进CRJ-LPA算法。该算法具体步骤如下:
Step1:初始化,根据节点ID为每个节点分配一个唯一的标签;
Step2:根据式6计算所有节点的重要性,并根据节点重要性由高到低对节点集合V进行排序;
Step3:根据式7计算节点的相似度;
Step4:从节点集合V中依次取出节点进行更新,并且优先更新邻居节点间具有最大影响力的节点,如果出现影响力相同的情况,则根据式8计算邻居节点的CRJ(v,v'),然后将节点v的标签更新为具有最高CRJ(v,v')的邻居节点v'的标签;其次,在标签更新过程中,如果节点的邻居节点中个数最多的标签出现两个或多个时,同样根据CRJ(v,v')来更新节点v的标签;
Step5:如果网络中的所有节点的标签均稳定不变,则循环停止并退出算法。否则,跳转到Step4继续循环。
3 实验结果与分析
选取Lesmis与Celegansneural两种国际上公认的真实数据集,对CRJ-LPA算法进行测试。算法的实验环境为Python3.5软件,硬件配置为i5-3230M,RAM:4.00G;软件配置:64 位WIN7操作系统。
3.1 有向加权网络模块度
文献[13]中Newman和Girvan提出了模块度的概念,后来作为衡量社区算法性能的公认评价标准。再后来,Newman等将其拓展到有向、加权网络上[16],定义如下:

3.2 实验结果
数据集Lesmis与Celegansneural是两种有向有权复杂网络数据集,其基本信息如表1所示。

表1 真实复杂的网络数据集信息
在这两种真实数据集上对算法进行分析与验证,并且根据模块度来衡量算法划分的社区结构的优劣。同时,将文中算法CRJ-LPA与传统LPA算法(如LPA、NSLPA、KBLPA算法)进行比较。不同算法分别在数据集上进行运算后的模块度如表2所示。

表2 算法模块度的比较
通过对表2中的实验数据进行分析可以看出,与传统的LPA、NSLPA、KBLPA算法相比,文中算法发现的社区结构的平均模块度最大。从上述精准的数字描述可以看出,文中算法在这两种有向有权复杂网络数据集上比传统LPA等算法在性能上有明显提升,且模块度的值均在良好社区结构的模块度区间[0.3,0.7]范围内。因此,文中算法划分的社区结构良好,且算法准确性和稳定性较高。文中算法与LPA算法对Lesmis数据集划分的结果如图2与图3所示。
图2和图3将位于不同社区的节点用直线分隔开,并且通过两幅图的对比可以得出,文中算法发现的社区较传统LPA算法所得社区数量多,且较为稳定,没有超大社区。
4 结束语
针对有向加权网络,提出了一种基于节点重要性和节点相似性的改进标签传播算法(CRJ-LPA)。该算法综合考虑了复杂网络中边的权值和方向性,并且采用标签传播的思想进行社区发现。首先,通过有向加权的ClusterRank算法获得节点的重要性排序列表,然后根据此顺序更新节点标签,提高社区结构的划分质量;其次,在节点更新过程通过节点重要性和相似性计算出一个新的度量CRJ,以此来避免原始LPA中的随机选择,有效克服了传统标签传播算法的随机性。通过真实数据集对算法进行测试,发现该算法具有较好的可行性和准确性,能够准确地衡量节点的重要性,而且与LPA算法具有相似的时间复杂度。

图2 文中算法效果

图3 LPA算法效果

