An Optimal Analysis for 3D Flow of Prandtl Nanofluid with Convectively Heated Surface
Malik Zaka Ullah and Metib Alghamdi
1Department of Mathematics,Faculty of Science,King Abdulaziz University,Jeddah 21589,Saudi Arabia
2Department of Mathematics,Faculty of Science,King Khalid University,Abha 61413,Saudi Arabia
Abstract In this paper,the magnetohydrodynamic 3D flow of Prandtl nanoliquid subject to convectively heated extendable surface has been discussed.A linear stretching surface makes the flow.Thermophoretic and Brownian motion impacts are explored.Heat transfer for convective procedure is considered.Prandtl liquid is taken electrically conducted through applied magnetic field.Suitable non-dimensional variables lead to strong nonlinear ordinary differential system.The obtained nonlinear differential systems are solved through optimal homotopic technique.Physical quantities like skin friction coefficients and Nusselt number are explored via plots.It is observed that effects of Hartman parameter and Biot number on temperature and concentration are quite similar.Both temperature and concentration are enhanced for larger values of Hartman parameter and Biot number.
Key words: three-dimensional flow,MHD,Prandtl fluid,nanoparticles,optimal homotopy analysis method(OHAM)
1 Introduction
Nanomaterials considered a main factor in industry development.Nanofluids are an important branch of nanomaterials,which were firstly referred by Choi[1]in 1995.Nanofluids are identified as a base fluid contains suspended small particles (1−100) nm.Water,oil,and alcohols are commonly base fluids.The importance of nanofluids is due to their unusual thermophysical properties.Nanofluids exhibit high ability to conduct electricity and heat,so it plays a vital role in industry.Before long nanofluid components have expanded vital centralization of researchers inferable from their entrancing warm transport in a couple of calm disapproved of fields.There are many applications such as engine cooling,cooling of electronics,refrigeration,solar water heating,microprocessors,laser applications and super conducting magnets.Jang and Choi[2]discussed the role of Brownian motion in the enhanced thermal conductivity of nanofluids.After that Brownian dynamics simulation to determine the effective thermal conductivity of nanofluids is reported by Bhattacharyaet al.[3]Buongiorno[4]presented complete model to analyze the aspects of thermophoresis and Brownian motion.Some continuous explores on nanofluid stream subject can be directed through the examinations.[5−30]
Flow of liquid on stretching sheet is now massively acknowledge by the researchers because of their large engineering and industrial application in rubber sheets,manufacture of food,glass fiber,hot rolling,paper production and many others.However liquid flow due to non-linear stretching sheet is scare.Rahimiet al.[31]considered collocation method to explore the solutions of an Eyring-Powell fluid caused by linear stretching sheet.Combined properties of viscous dissipation and MHD on the micropolar nanofluid on stretching sheet have been examined by Hsiao.[32]Zhanget al.[33]analyzed the unsteady flow of Oldroyd-B nanofluid because of stretching sheet.Hayatet al.[34]investigated stretched flow of Jeffery fluid.Recently researchers have investigated the flow of non-Newtonian and Newtonian liquids over non-linear stretching sheet.Seth and Mishra[35]used the Navier’s slip condition to study the transient flow of nanofluid past a non-linear stretching sheet.Hussainet al.[36]studied the characteristics of tangent hyperbolic fluid along non-linear stretching sheet by using convective boundary conditions.Hayatet al.[37]explored the non-linear stretched flow of second grade fluid.Nanofluid flow with variable thickness comprising electrical MHD in the non-linear stretched sheet is discussed by Danielet al.[38]
Magnetohydrodynamic is the study of magnetic behavior in electrically conducting fluids.Plasmas,salt water and liquid metals are examples of such fluids.In Physics,Hannes Alfv´en achieved Nobel Prize in 1970 for his great work on MHD.Magnetohydrodynamic is important in astrophysics,space plasma physics,cancer tumor treatment,solar physics,blood pump machine,and laboratory plasma experiments.Ishaket al.[39]considered MHD flow past a radially shrinking or stretching disk.Huang and Liu[40]attempted to combine fluid hammer effect with MHD effect.Hayatet al.[41]computed numerical results for MHD flow with Soret and Dufour effects.Hayatetal.[42]studied three-dimensional flow due to exponentially stretching surface in the existence of an applied magnetic field and Joule heating effects.Second grade nanofluid with MHD over a nonlinear stretching surface is studied by Hayatet al.[43]Tamooret al.[44]discussed MHD Casson flow between stretching cylinder.
The prime purpose of present topic is to illustrate hydromagnetic 3D stream of Prandtl liquid[45−48]inside seeing nanoparticles.Thermal and mass trade properties are portrayed through random spread and thermophoresis.Prandtl liquid is taken driving through uniform associated alluring field.Thermal convective condition[49−50]and a condition related with zero nanoparticles change[51−52]are completed at the farthest point.The obtained nonlinear differential systems are solved through optimal homotopic analysis method (OHAM).[53−59]Effects of a couple of physical variables are inspected.In addition the coefficients of surface drag and warmth conversion standard are explored graphically.
2 Formulation
We inspect steady hydromagnetic three-dimensional(3D) flow of Prandtl nanoliquid by a linear deformable surface.Thermal condition and as of late made necessity are requiring zero nanoparticles movement are constrained at the point of confinement.Brownian advancement and thermophoretic effects are investigated.The fluid is assumed to be conducted electrically with magnetic fieldB0applied parallel toz-direction.For very small Reynolds number current hall and magnetic field effects are ignored.Cartesian coordinate system is incorporated.The sheet is stretched alongx- andy-directions atz= 0 with velocitiesUwandVw.Boundary layer expressions governing the flow of Prandtl nanofluid in the absence of viscous dissipation and thermal radiation are written as follows:[16,48]
Here one has the following conditions:[16,48]
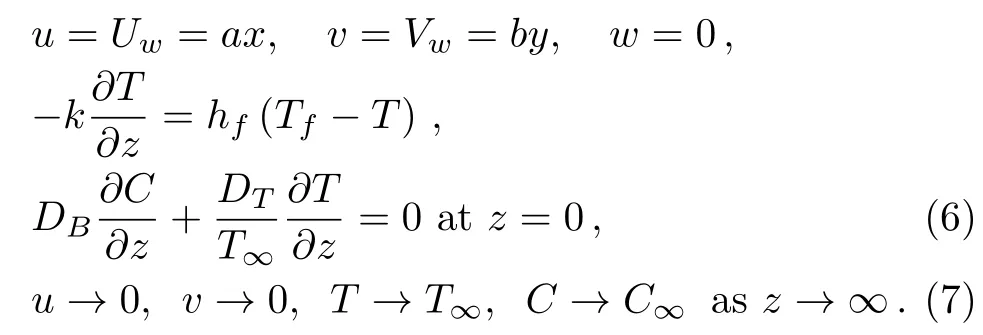
Hereu,v,andwspeak to the speeds inx-,y-,andzbearings,µthe dynamic consistency,ν(=µ/ρf)the kinematic thickness,kthe warm conductivity,ρfthe thickness,Aandcthe material constants of Prandtl fluid model,σthe electrical conductivity,α⋆=k/(ρc)fthe warm diffusivity,(ρc)fthe warmth capability of the fluid,(ρc)pthe powerful warmth capability of nanoparticles,Tthe temperature,DBthe Brownian development,Cthe focus,DTthe thermophoretic dispersion andT∞andC∞the encompassing liquid temperature and fixation.Considering

Expression(1)is naturally fulfilled and Eqs.(2)−(7)have the accompanying structures

Hereβ1remains for Prandtl fluid number,β2for flexible number,Hafor Hartman parameter,αfor ratio parameter,Prfor Prandtl number,γfor Biot number,Nbfor Brownian development parameter,Ntfor thermophoresis number andScfor Schmidt number.These parameters are characterized by:

The physical quantities are given by

It is seen that mass motion spoken to by Sherwood number is presently indistinguishably evaporates andRex=Uwx/νandRey=Vwy/νdelineate nearby Reynolds parameters.It is also noticed that the Prandtl fluid model reduces to viscous fluid case whenβ1=1 andβ2=0.
3 OHAM Solutions
It has been noted that Eqs.(9)–(12)along with boundary conditions (13) and (14) are four non-linear ordinary differential equations whose optimal series arrangements have been developed by employing OHAM.The initial deformations (f0,g0,θ0,ϕ0) and auxiliary linear operators(Lf,Lg,Lθ,Lϕ) are
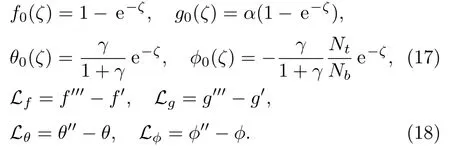
The above linear operators obey

4 Convergence Analysis
We have unwound the power,essentialness and center verbalizations with the help of BVPh2.0.These verbalizations contain cloud factorsWe can process the base estimation of these elements by taking total mix-up pretty much nothing.In the packaging of HAM,these elements expect a basic employment.That is the reason these variables insinuate as association control parameter,which shifts HAM from other illustrative conjecture systems.With a particular ultimate objective to diminish the CPU time,we have used typical waiting errors at them-th order of theory which are described by
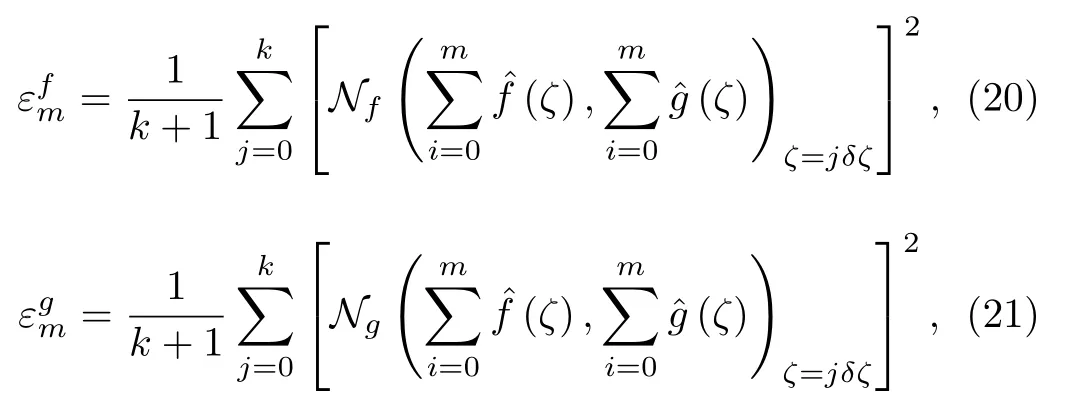

HereNf,Ng,Nθ,andNϕdenote the non-linear operators corresponding to Eqs.(9)–(12) respectively.Following Liao:[53]
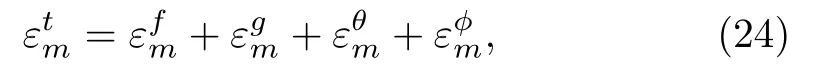
whereεtmindicates add up to leftover squared blunder,k= 20 andδζ= 0.5.Ideal information for assistant parameters at second request of approximations is=−1.591 89,=−3.056 54,=−1.365 14,=−1.186 26 andεtm= 9.39×10−4.Figure 2 speaks to related aggregate remaining mistake plot.Table 1 illustrates normal square residual errors.It has been dissected that the normal averaged square errors decrease with higher request disfigurements.
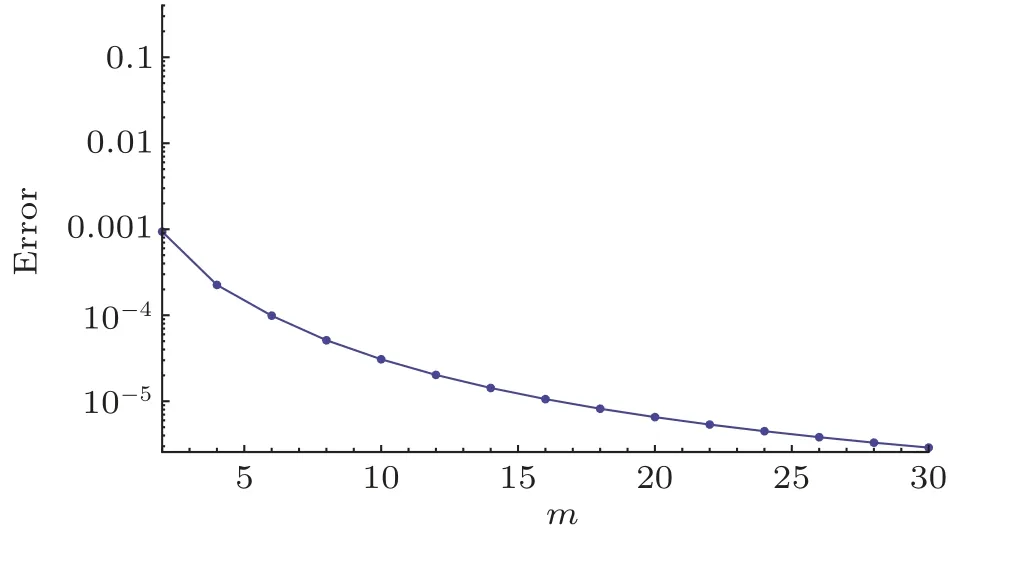
Fig.1 Total residual error plot.

Table1 Averaged normal residual square errors utilizing ideal information of helper factors.

Fig.2 θ(ζ)variation forβ1.
5 Graphical Results and Discussion
This section researches impacts of two or three significant physical stream factors like Prandtl liquid parameterβ1,adaptable parameterβ2,Hartman numberHa,extent numberα,Biot parameterγ,Prandtl parameterPr,Schmidt parameterSc,Brownian improvement parameterNband thermophoresis numberNton temperatureθ(ζ)and focusϕ(ζ).Figures 2 and 3 are constructed to presentθ(ζ)for different estimations ofβ1andβ2.It is noted from these figures that increase inβ1andβ2leads to decrease in temperature.Figure 4 displays the variations of Hartman numberHaon temperature profileθ(ζ).Lorentz force arises inHathat resists the fluid motion therefore temperature fieldθ(ζ) enhances.Figure 5 demonstrates that an adjustment in extent numberαprompts a poor temperatureθ(ζ) and less layer of warm.Impact of Biot numberγonθ(ζ)is depicted in Fig.6.Increase inγcauses a powerful convection that display an increment inθ(ζ).Figure 7 shows that temperature diminish for greater values of Prandtl number.As greaterPrcorresponds to lower thermal diffusivityαwhich causes decrease in temperature.Figure 8 is constructed to study the influence of thermophoresis parameter on the temperature field.This figure illustrates that increase in thermophoresisNtparameter tends to higher temperature.This parameter is occurred due to nanomaterials.The existence of nanomaterials raised the thermal conductivity of nanoliquids.Nanofluid thermal conductivity is an increasing function of temperature.That is why enhancement in temperature is observed for greater estimation ofNt.Figures 9 and 10 elucidate that nanoparticles concentration is smaller for greater values ofβ1andβ2(material parameters).Figures 11 and 12 are plotted to analyze the change inϕ(ζ)for larger Hartman number and extent parameterα.We observed that increasing and decaying impacts occur for both dimensionless parameters on concentration profile.Figure 13 shows the consequences of Schmidt number onϕ(ζ).Schmidt number relates to the mass diffusion of a system.AsScis increased mass diffusion decreases due to which concentration shows decreasing trend.Brownian parameterNbwhen increased causes a change in the Brownian motion of nanoparticles which reduces the distribution of concentration as depicted by Fig.14.IncreasingNtcauses increase in thermal conductivity of the system which contributes in increase of concentration as seen in Fig.15.Figure 16 presents impact ofHaandβ1onCfRe1/2x.It has been seen thatCfRe1/2ximproves forHa.Figure 17 demonstrates the effects ofαandβ1onCfRe1/2x.ObviouslyCfRe1/2xdemonstrates expanding conduct forαandβ1.Figure 18 demonstrates the impacts ofHaandβ1onCgRe1/2y.An upgrade inHaindicates expanding conduct forCgRe1/2y.Figure 19 demonstrates the impacts ofαandβ1onCgRe1/2y.From this Figure it has been broke down thatCgRe1/2yis a hoisting capacity ofα.Impact ofNbandNtonNuxRe1/2xare uncovered through Fig.20.HereNuxRe1/2xdiminishes forNtwhile steady pattern is seen forNb.Table 2 shows the comparison for different values ofαwith homotopy perturbation method (HPM) and exact solutions.Table 2 presents an excellent agreement of OHAM solutions with the existing homotopy perturbation method (HPM) and exact solutions in a limiting sense.
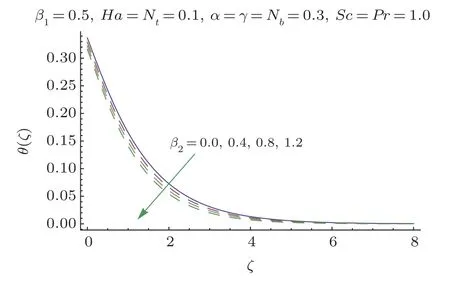
Fig.3 θ(ζ)variation forβ2.
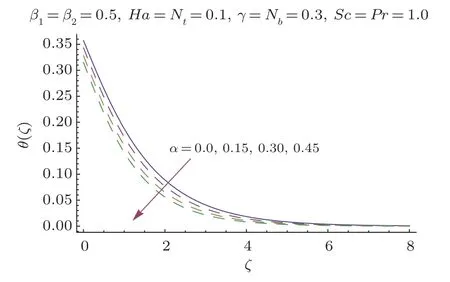
Fig.5 θ(ζ) variation forα.

Fig.6 θ(ζ) variation forγ.
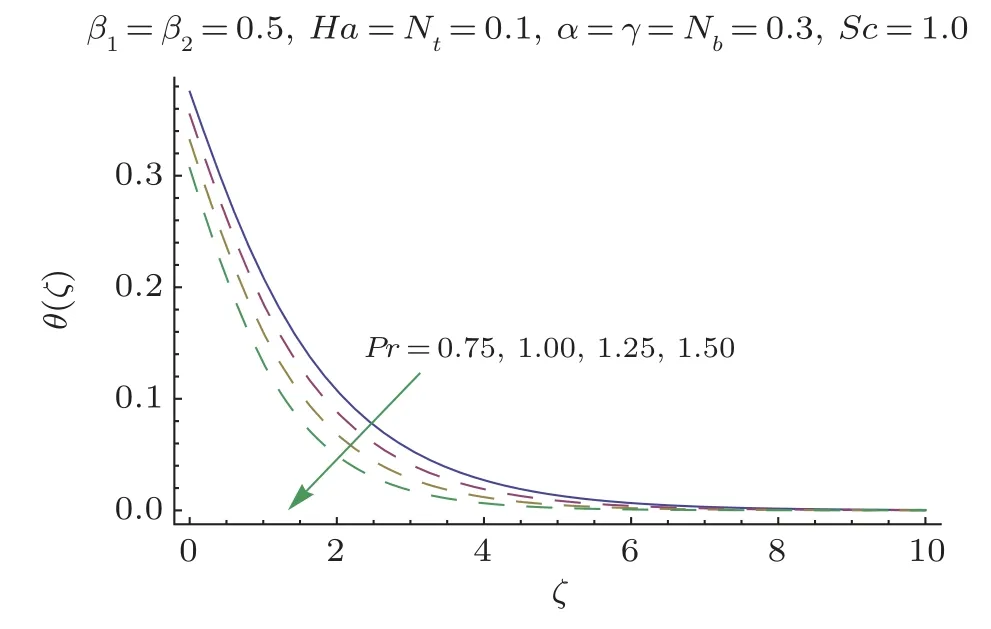
Fig.7 θ(ζ) variation forPr.

Fig.8 θ(ζ)variation forNt.

Fig.9 ϕ(ζ)variation forβ1.

Fig.10 ϕ(ζ) variation forβ2.
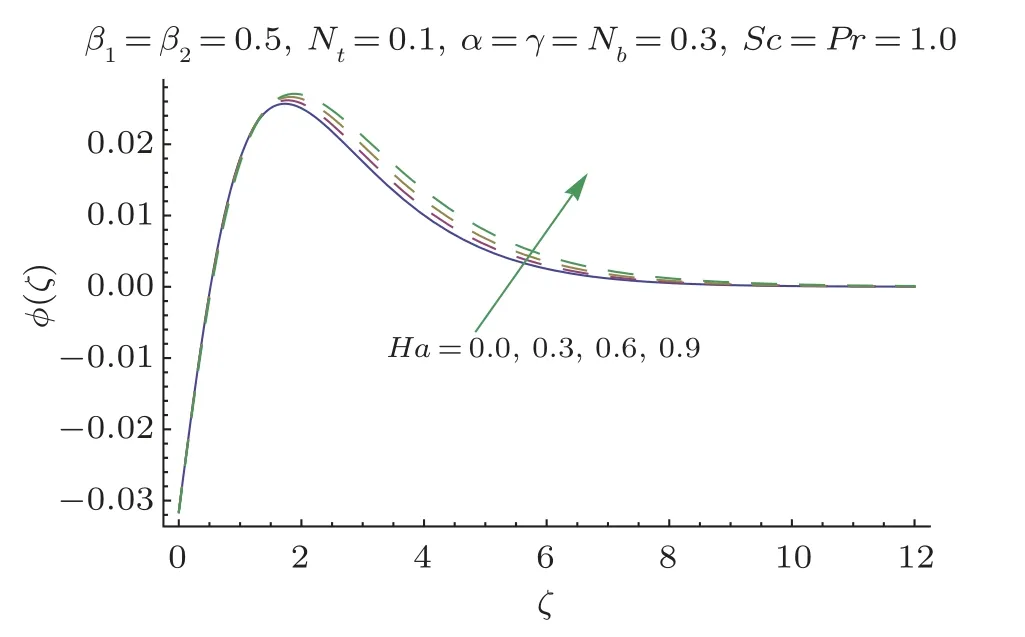
Fig.11 ϕ(ζ)variation forHa.

Fig.12 ϕ(ζ) variation forα.

Fig.13 ϕ(ζ)variation forSc.

Fig.14 ϕ(ζ)variation forNb.

Fig.15 ϕ(ζ)variation forNt.
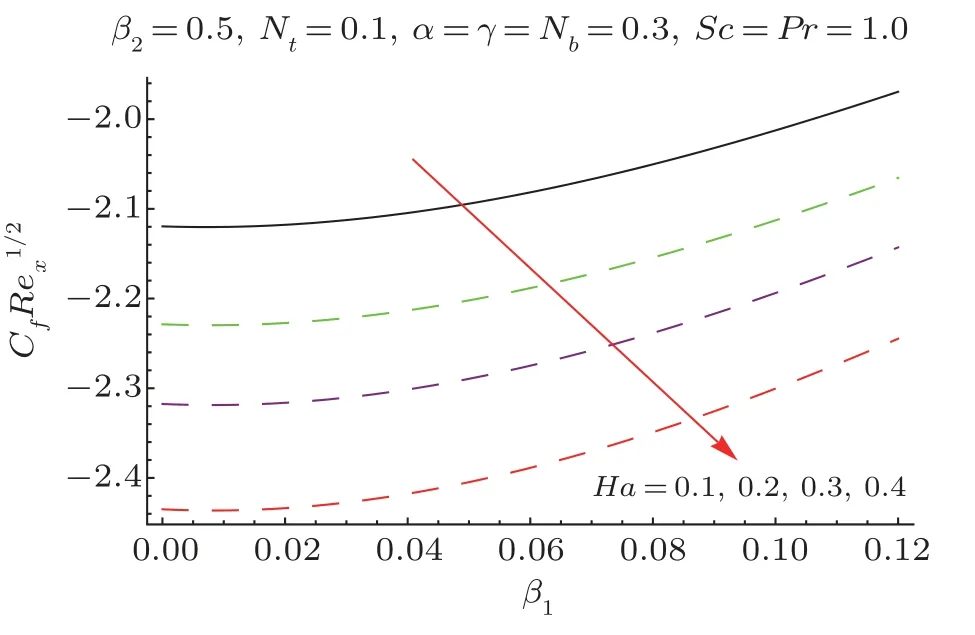
Fig.16 Plots ofCfRe1/2x viaHa andβ1.

Fig.17 Plots ofCfRe1/2x viaα andβ1.

Fig.18 Plots ofCgRe1/2y viaHa andβ1.
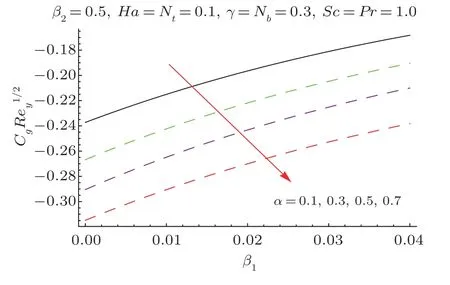
Fig.19 Plots ofCgRe1/2y viaα andβ1.
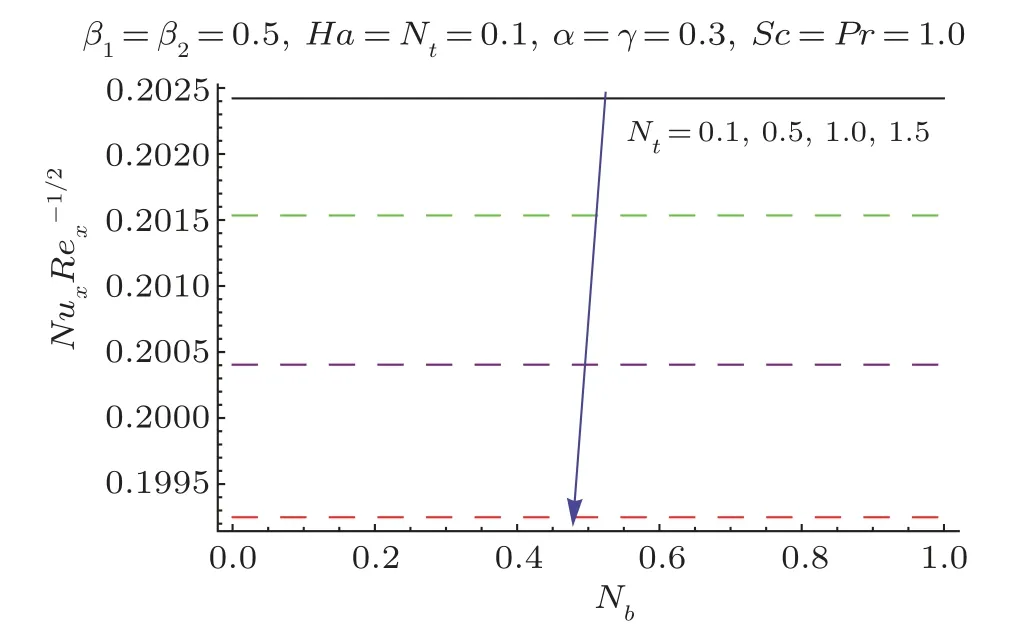
Fig.20 Plots ofNuxRe−1/2x viaNb andNt.
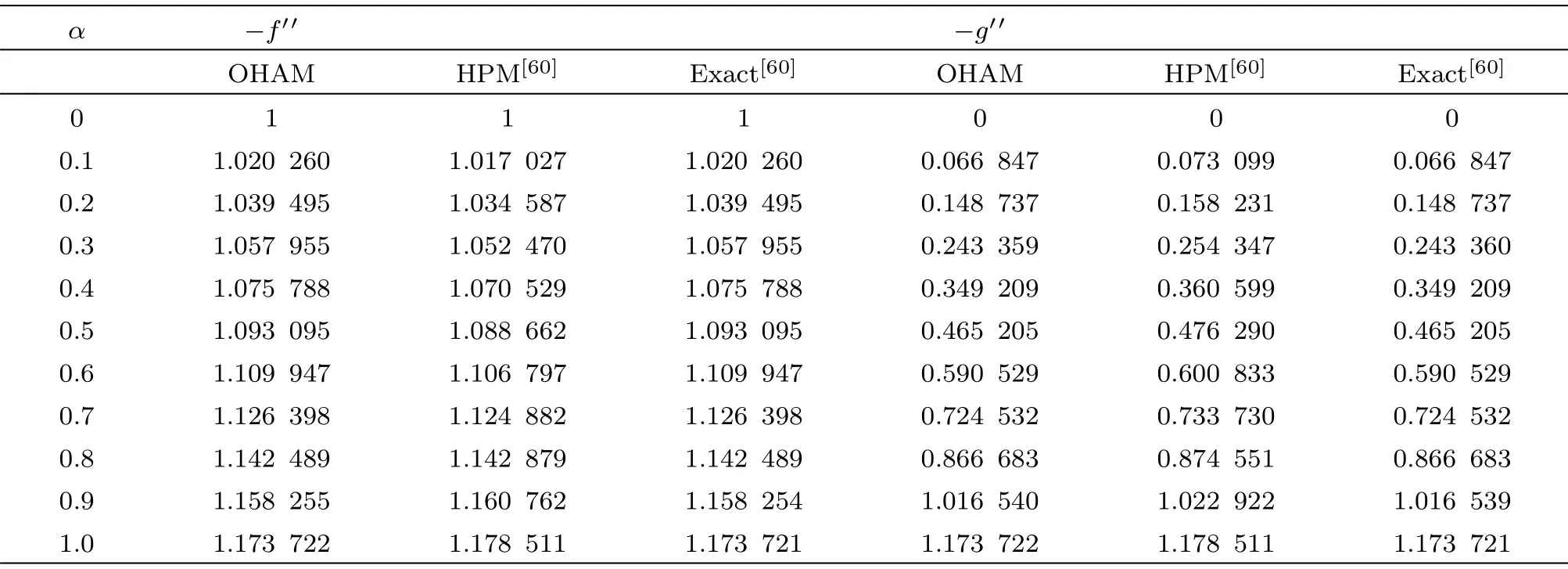
Table2 Comparative values of−f′′(0) and−g′′(0) for several values ofα whenβ1 =1 andβ2 =Ha=0.
6 Conclusions
Here hydromagnetic 3D limit layer stream of Prandtl nanoliquid as a result of straightly deformable surface with convective surface condition is performed.Genuine consequences of the current analysis are sketched out as seeks after:
•Both temperatureθ(ζ) and fixationϕ(ζ) fields show decaying design for higher Prandtl liquidβ1and adaptableβ2parameters.
•An expansion in Hartman numberHademonstrates more grounded temperatureθ(ζ) and fixationϕ(ζ) fields.
•Higher proportion numberαdelineate lessening conduct for concentrationϕ(ζ) and temperatureθ(ζ) fields.
•Higher Biot numberγindicates more grounded temperatureθ(ζ) field.
•Similar behavior is observed for different values ofNton concentrationϕ(ζ) and temperatureθ(ζ) fields.
•For higher estimations of Prandtl parameterPr,temperatureθ(ζ) decreases.
•An increment in Schmidt numberScyields weaker Concentrationϕ(ζ) field.
•Concentrationϕ(ζ) field exhibits decaying trend via Brownian advancement numberNb.
Acknowledgment
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through Research Groups Program under grant number (R.G.P2./19/40).
 Communications in Theoretical Physics2019年12期
Communications in Theoretical Physics2019年12期
- Communications in Theoretical Physics的其它文章
- Magnetohydrodynamic Stagnation Point Flow of a Maxwell Nanofluid with Variable Conductivity
- The Effects of Wettability on Primary Vortex and Secondary Flow in Three-Dimensional Rotating Fluid∗
- An Improved Heterogeneous Mean-Field Theory for the Ising Model on Complex Networks∗
- Relativistic Self-Focusing of Hermite-cosh-Gaussian Laser Beam in Magnetoplasma with Exponential Plasma Density Ramp
- Periodic Orbits Around Kerr Sen Black Holes∗
- Parameterized Post-Post-Newtonian Light Propagation in the Field of One Spherically-Symmetric Body∗
