Periodic Orbits Around Kerr Sen Black Holes∗

Chang-Qing Liu (刘长青), Chi-Kun Ding (丁持坤), and Ji-Liang Jing (荆继良)

1Department of Physics,Hunan University of Humanities Science and Technology,Loudi 417000,China

2Department of Physics,and Key Laboratory of Low Dimensional Quantum Structures and Quantum Control of Ministry of Education,Hunan Normal University,Changsha 410081,China

Abstract We investigate periodic orbits and zoom-whirl behaviors around a Kerr Sen black hole with a rational number q in terms of three integers (z,w,v),from which one can immediately read off the number of leaves (or zooms),the ordering of the leaves,and the number of whirls.The characteristic of zoom-whirl periodic orbits is the precession of multi-leaf orbits in the strong-field regime.This feature is analogous to the counterpart in the Kerr space-time.Finally,we analyze the impact of the charge parameter b on the zoom-whirl periodic orbits.Compared to the periodic orbits around the Kerr black hole,it is found that typically lower energies are required for the same orbits in the Kerr Sen black hole.

Key words: periodic orbits,Kerr Sen black hole,zoom-whirl,rational number

1 Introduction

Periodic orbits have played a crucial role in the treatment of some difficult problems in celestial mechanics,including the motions of planetary satellites,the long term stability of the solar system,and motion in galactic potential.It is fact that the relativistic precession of Mercury’s perihelion in the weak field is around a star.In the strong-field,perihelion precession in the equatorial plane of a black hole can result in zoom-whirl orbits for which the precession is so great at closest approach that the particle executes multiple circles before falling out to apastron again.The Laser Interferometer Gravitational-wave Observatory (LIGO)[1−3]and VIRGO collaborations reported the observation of gravitational-wave signal corresponding to the inspiral and merger of two black holes is also relevant to this relativistic trajectories.In a series of papers.[4−8]Levinet al.,proposed a classification of the zoom-whirl structure of the periodic orbits around black hole by using Kerr geodesics[9−19]with a rational numberqin terms of three integers (z,w,v),

wherewcounts the number of whirls,zcounts the number of leaves,andvindicates the order in which the leaves are traced out.The rational numberqexplicitly measures the degree of perihelion precession beyond the ellipse as well as the topology of the orbit.This classification is applied to black hole pairs,they found that zoom-whirl behavior is ubiquitous in comparable mass binary dynamics and entirely quantifiable through the spectrum of rational.This zoom-whirl behavior is also found in the Reissner-Nordström black hole[7]and spherically symmetric naked singularity,[20]Kehagias-Sfetsos black hole.[21]Furthermore,periodic orbits are generalized from the equatorial taxonomy to fully generic 3D Kerr motion.[8]

The Kerr-Sen black hole (KSBH) solution[22]is a charged and rotating solution in the low energy limit of heterotic string theory and is also characterized by mass,electric charges,and angular momentum,which are similar to those of the Kerr Newman black hole.Some distinguishable properties and various aspects of particle motion[23−30]in those space-times have been studied.Based on a topological taxonomy of periodic orbit,in this paper,we will use Levin’s[4]classification scheme to investigate the zoom-whirl behavior and orbital dynamics in the equatorial plane of the KSBH.We will use specific features of the periodic orbits to distinguish KSBH from Kerr black hole.

The paper is organized as follows: In Sec.2,we first derive the relevant geodesic equations of KSBH using the Hamiltonian formulation.In Sec.3,we investigate the innermost bound and stable circular orbits,as well as a qualitative analysis of the effective potential.In Sec.4,the energy of zoom-whirl periodic orbits in the KSBH is studied.Finally,we end the paper with a summary.

2 The Time-Like Geodesic Equations in the Kerr Sen Black Hole

In Ref.[22],Sen obtained a four-dimensional solution that describes a rotating and electrically charged massive body in the low energy heterotic string field theory.In the Boyer-Lindquist coordinates,the Kerr-Sen metric can be rewritten as

where the functions ∆andρ2are given by

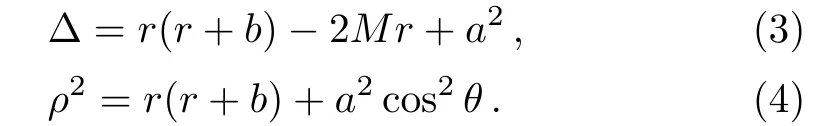
HereMis the mass of the black hole,ais the specific angular momentum of the black hole,b=Q2/M,Qbeing the electrical charge of the black hole.In the particular caseb=0,the above solution is reduced to the Kerr one.The event horizon of the KSBH is located at

The Hamiltonian of a time-like particle propagating along geodesics in a Kerr Sen black hole can be expressed as

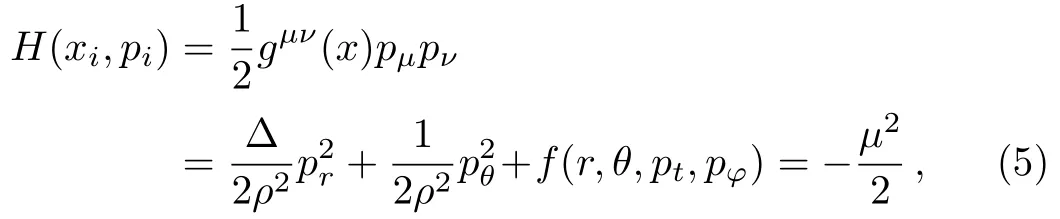
whereµis the mass of particle.It is easy to obtain two conserved quantities: the energyEand angular momentumLof the test particles with the following forms

The first integral from the geodesic equations in case of the KSBH are calculated as follows.[23−30]Following the procedure in Ref.[4],we will convert the first integral equations into Hamiltonian formulation to avoid the numerical difficulties and smoothly plot the time-like zoomwhirl orbits.With the help of Hamilton’s equations

the equations of the time-like particle motion become as,

with

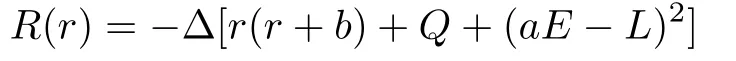
where the superscripts′andθdenote differentiation with respect torandθ,respectively.The quantityQis the generalized Carter constant related to the constant of separationKbyQ=K −(aE −L)2.In this paper we only deal with the motion of bounded time-like (µ= 1) particles in the equatorial plane,for which motion lies in the 4D hypersurface defined byθ=π/2,and on whichQ=0.

3 Bound on Angular MomentumL

As mentioned in Ref.[4],in order to have a sufficiently rich variety of zoom–whirl periodic orbits,the angular momentumLof the particle should satisfies

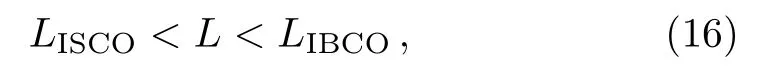
where ISCO stands for“Innermost Stable Circular Orbit”and IBCO for “Innermost Bound Circular Orbit”.LISCOis the lowest value ofLfor which the potential has a local minimum.ForL < LISCO,all orbits will plunge into the black hole,soLISCOsets the lower limit on bound orbits.LIBCOmarks the first appearance of an unstable circular orbit that is energetically bound.It sets the upper limit only in the sense that we expect to see the most zoom-whirl behavior.From the geodesics,the conditions to determine the ISCO are

which yield

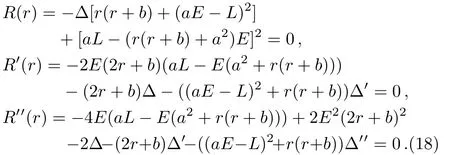
For the non-rotating black hole,these equations can be solved simultaneously forEandLto give

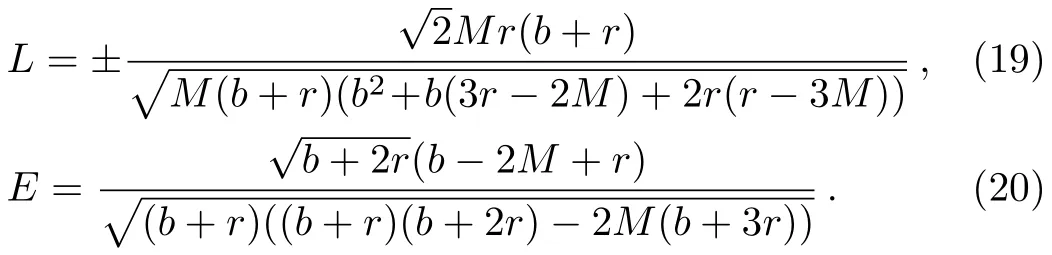
And the radius of the ISCO is given by

Whenb=0,one will getrISCOfor the Schwarzschild black hole,

The radius of the IBCO is given from the conditionE=1,[31]

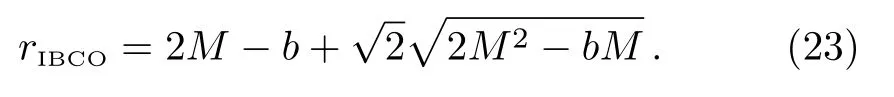
While when0,no analytical result is available.Nevertheless,we can obtain a numerical solution.The results are listed in Fig.1 for prograde orbit.For the prograde ISCO and IBCO,both the angular momentumLISCOandLIBCOdecreases with the black hole spinaand the charge parameterb.

For a non-spinning black hole (a=0),we can rewrite the radial equation as the expression of effective potential

with

this effective potentialVeffis a different function ofrfor each fixedLand is independent ofE.The result is a simple visual way to describe the different types of allowed motion asLis varied.However,the effective potentialVeffof the spinning Kerr Sen black hole is dependent ofE.We therefore lose the ability to visualize easily the variation of orbits with energy.A useful pseudo-effective potential[7]is constructed through the conditionR(r)=0 as

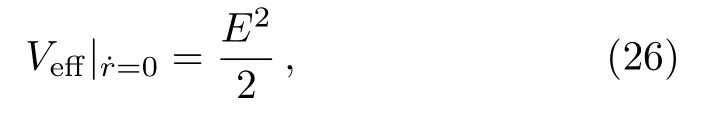
with

Even if the difference betweenEand the value ofVeffno longer gives the value of ˙r2,this pseudo-effective potential illustrates the change of periodic orbits with energy.

Fig.1 (Color online) Angular momentumLIBCO andLISCO vs.a in the Kerr Sen black hole,with Parameterb = 1,0.8,0.6,0.4,0.2,0 from left to right,here we setM =1.

Figure 2 depicts the influence of the charge parameterbto the effective potential.The maximum value of the effective potential decreases with the increasing of the charge parameterb.

Fig.2 (Color online) Effective potentials with different the charge parameterb for the corresponding angular momentumL =Lav = (LISCO+LIBCO)/2 in the Kerr Sen black hole: in (a),parameter takes the valueb = 0,0.2,0.4,0.6,0.8,1 from top to bottom; in (b),parameter takes the valueb = 0.69,0.6,0.4,0.2,0 from left to right.Here we setM =1.

Notice that the corresponding angular momentumLof the effective potential takes the valueLav[20](the average value ofLISCOandLIBCO)

this would give an appropriate potential well for any parameterbthat captures most of the physics of the bound orbits.In the last section 5,the angular momentumLalso takes the valueLavas we analyze the impact of the charge parameterbon the energy of the periodic orbit,in order to have a sufficiently deep potential well that supports a wider variety of orbits.

4 Periodic Orbits in Kerr Sen Black Hole

In this section,we shall study zoom-whirl periodic orbits around the KSBH.We use the taxonomy of orbit of Levinet al.[4−7]to derive the association between periodic orbits and rational numbersqfrom the dynamical systems perspective.Any bound orbit may be characterized by two fundamental frequencies–the libration in the radial coordinate,ωr,and the rotation in the angular coordinate,ωφ.Zoom-whirl periodic orbit corresponds to trajectories where the ratio of these two frequencies is a rational numberqin terms of three integers (z,w,v),

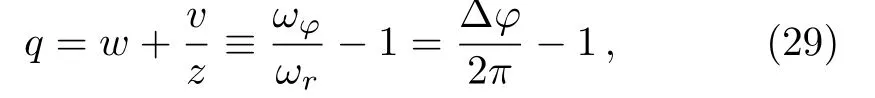
where ∆φ=∫Tr(dφ/dt)dtis the equatorial angle accumulated in one radial cycle from apastron to apastron.By this definition,we see thatqis the amount an orbit precesses beyond the closed ellipse.These three quantitiesz,w,vhave a geometric interpretation in terms of the structure of the trajectory,wherezis the ‘zoom’ number,wis the number of “whirls”,andvis the number of vertices formed by joining the successive apastra of the orbits.[4]Thus the trajectory will close and the particle returns to its initial state within a finite(affine)time,thus executing its prior trajectory repeatedly.

Using the geodesic equations of the KSBH,we get the expression of the rational numberq,

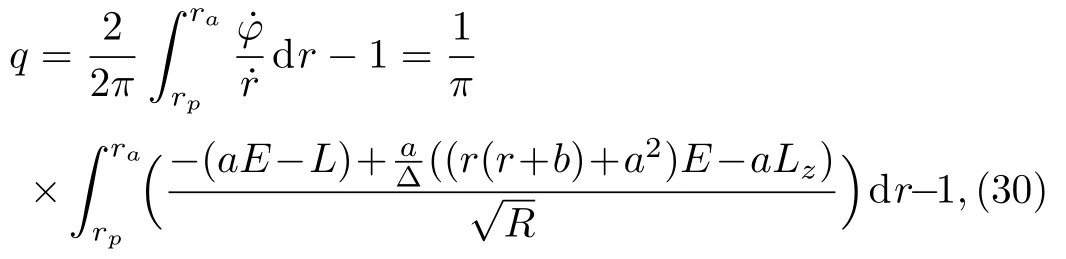
whererpandrais the periastron and apastron of the zoom-whirl orbit,respectively.In the equatorial plane,one of the roots is always 0 andRcan be written as

Now the rational numberqis a function ofq(a,b,E,L,r0,rp,ra).To haveqas a function of(a,b,E,L)only,we have to findr0,rp,raas functions of(a,b,E,L).Thus we expand the polynomial

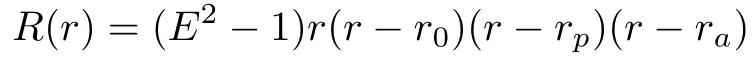
and equate to the definition ofR(r)in Eq.(14),matching up coefficients in powers ofrand finding a system of equations forr0,rp,ra.Sincer= 0 is always a root,this is equivalent to a 3rd order equation inrand cubic equation have a generic solution.The cubic equation is given as

with

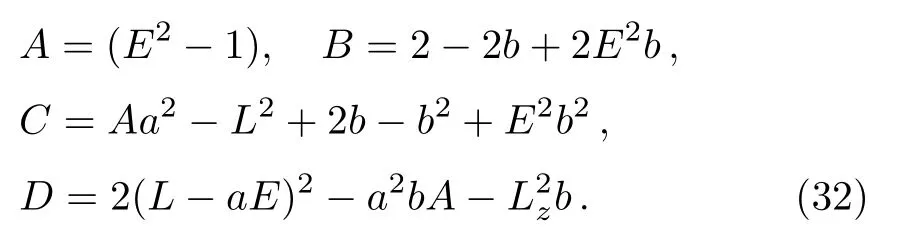
The nonzero roots in ascending order are

where

We now have established a simple relationship between rational numberqand the quantitiesa,b,LandE,by inputting the value ofz,wandvfor a givena,bandLto locate theE,apastronraand perihelionrpof the corresponding periodic orbit.

In Fig.3,we depict zoom-whirl periodic orbits with variouszvalues.Whenzincreases from 1 to 4,the leave of the zoom-whirl periodic orbits varying from one leaf to four leaves.So “z” is visualized as the number of leaves,or“zoom”in the particle orbit.Figure 4 shows orbits with variouswvalues,every object travels at least a full from 4πaround to 8πthe central black hole aswincreases from 1 to 3.It means that the number of extra turns around the center of the geometry gives us the value ofw.Figure 5 illustrates zoom-whirl orbits with variousvvalues,red line shows that the zoom-whirl orbits withv=1 andv= 3 move along the different trajectory; the energy of the zoom-whirl orbit withv=3 is higher than the zoomwhirl orbit withv=1.

Fig.3 (Color online)Zoom-whirl periodic orbits withq =w+v/z =1+1/z,(z =1,2,3,4)fora=0,b=0.2,L=3.8,here we setM =1.

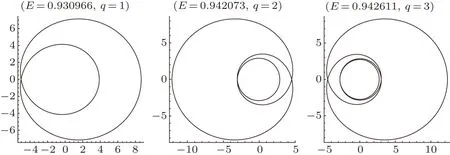
Fig.4 (Color online)Zoom-whirl periodic orbits withq =w+v/z =w+0/1,(w =1,2,3)fora=0.6,b=0.1,L=2.9,here we setM =1.

Fig.5 (Color online) Zoom-whirl periodic orbits withq =w +v/z = 1+v/4,(v = 1,3) fora = 0,b = 0.2,L=3.8,here we setM =1.

Finally,we must address the degeneracy that arises when the quotientv/zis a reducible fraction.Thus we require thatv/zis an irreducible fraction.Asqhave approximate values,the zoom-whirl orbit is precessions.For instance,v/z=42/125≈1/3,the orbit withq=167/125 is the precessions of the orbit withq= 4/3.Figure 6 shows several pairs of the precession orbits.All orbits withz= 1,2,3,4 are drawn.Between each of these low leaf orbits,randomly selected high zoom orbits are shown as well.The high zoom orbits (the second and fourth rows of Fig.6) look like precessions of the low zoom orbits (the first and third rows of Fig.6).[4]That is to say,any aperiodic orbit will be arbitrarily well approximated by a nearby periodic orbit.

5 Energy of Generic Orbits

Zoom-whirl periodic orbits give us a way to visually inspect orbits in different space-time to understand whether we can distinguish the KSBH from the Kerr black hole.So now we analyze the impact of the charge parameterbon the zoom-whirl periodic orbits.Transitions in the periodic orbits can be observed when the energyEand angular momentumLchanges,which emanate in the form of gravitational waves.Rational numberq,as a function ofq(a,b,E,L),contains the information on transitions in the periodic orbits during the inspiral stage.Figures 7 and 8 indicate that rational numberqmonotonically increases withEand decreases withLwhen the charge parameterbtakes the values 1,0.8,0.6,0.4,0.2,and 0 in both the rotating and not-rotating KSBHs.Taking(z=1,2,3,4,w=1,v=1)andLav=(LIBCO+LISCO)/2,we list the corresponding energy for each periodic orbit in Tables 1 and 2.It is shown that the corresponding energyEfor each periodic orbit decreases with the charge parameterb.It implies that the particles in the KSBH with angular momentumLavin a sufficiently deep potential well possess a richer variety of bound periodic orbits and a wider range of energyEthan their Kerr black hole counterparts.

Table1 The energy values of (z = 1,2,3,4,w = 1,v = 1) orbits around the non-rotating (a = 0) Kerr sen black hole for variousb are presented with their corresponding angular momentum,Lav =(LIBCO+LISCO)/2.

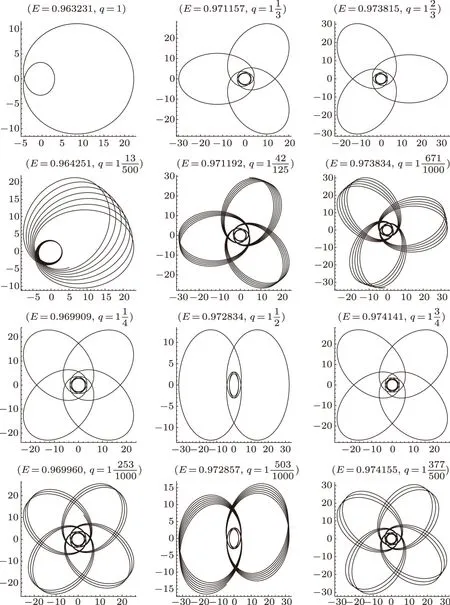
Fig.6 (Color online) A series of periodic orbits witha = 0.6,b = 0.18,L = 3,M = 1.Notice that the highz orbits look like precessions of the energetically closest lowz.

Fig.7 (Color online) The variation ofq as a function of energyE and angular momentumL for different values ofb in non-rotating KSBH:decreasing from left to right the values are 1,0.8,0.6,0.4,0.2,and 0.In(a),for eachb depicted above,the corresponding angular momentum isLav =(LIBCO+LISCO)/2.In(b),energy is kept fixed when(z,w,v)=(2,1,1).

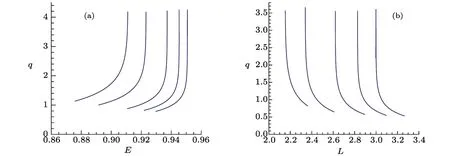
Fig.8 (Color online) The variation ofq as a function of energyE and angular momentumL for different values of the charge parameterb in Kerr sen black hole with the fixed rotating parametera = 0.6: decreasing from left to right the values are 0.69,0.6,0.4,0.2,and 0.In (a),for eachb depicted above,the corresponding angular momentum isLav =(LIBCO+LISCO)/2.In (b),energy is kept fixed when (z,w,v)=(2,1,1).

Table2 The energy values of (z = 1,2,3,4,w = 1,v = 1) orbits around the rotating (a = 0.6) Kerr sen black hole for variousb are presented with their corresponding angular momentum,Lav =(LIBCO+LISCO)/2.

6 Summary

In this paper,we have studied periodic orbits in the equatorial plane around the KSBH with a rational numberqin terms of three integers (z,w,v) under the taxonomy of orbit of Levinet al.[4−8]By using the Hamiltonian formulation,the geodesic motion of a time-like particle in the KSBH was analyzed,and the bound on the innermost bound and stable circular orbits were also calculated.We found that the angular momentumLISCOandLIBCOdecreases with the black hole spinaand the charge parameterb.We showed that all eccentric periodic orbits around the KSBH show zoom whirl behavior of some kind for the angular momentum of the time-like particles in the regionLISCO< L < LIBCO.The characteristic of the zoomwhirl periodic orbits is a spectrum of multi-leaf clovers structure,what’s more,aperiodic orbits will look like precessions of low-leaf clovers in the strong-field regime.This feature is qualitatively similar to those in the Kerr spacetime.Finally,we analyzed the impact of the charge parameterbon the zoom-whirl periodic orbits to distinguish the KSBH from the Kerr black.We found that periodic orbits around the KSBH occur at lower energies than their Kerr black hole counterparts.These results may provide us a possible observational signature by testing these periodic orbits around the central source to distinguish the KSBH from the Kerr black hole.