一种婴儿哭声识别优化算法的研究
2
(1.江南大学 物联网工程学院,江苏 无锡 214122; 2.江南大学 轻工过程先进控制教育部重点实验室,江苏 无锡 214122)
哭声是婴儿与外界沟通的信号,通常被婴儿用于表达一定的需求。婴儿哭声识别的常见方法是先对哭声信号进行端点检测和预处理,然后从预处理后的哭声信号中提取特征参数序列,特征参数有Mel频率倒谱系数(Mel Frequency Cepstrum Coefficient,MFCC),线性预测倒谱系数(Linear Prediction Cepstrum Coefficients,LPCC)[1]等,最后从特征序列中提取模板序列,并采用匹配算法进行判断。匹配算法有动态时间规整(Dynamic Time Warping,DTW)、隐马尔可夫模型[2](Hidden Markov Model,HMM)等。
在文献[3]中,作者使用MFCC参数作为婴儿哭声的特征,并使用DTW匹配算法对婴儿的哭声进行识别。文献[4]中,作者使用线性预测系数(LPC)作为特征,并且使用DTW匹配算法进行识别。文献[3]和文献[4]的婴儿哭声识别方案在理想情况下均有较好的正确率。但在实际使用中,往往会存在环境噪声,环境噪声会影响算法端点检测和特征提取的准确性,影响婴儿哭声识别准确率;此外每个婴儿存在个体差异,他们的基音频率不尽相同,所以哭声的频率分布也不同,从而导致识别算法在不同个体之间效果不同,算法鲁棒性下降。因此,如何获得一个实时性好且在噪声背景和不同婴儿个体之间也有较好的鲁棒性的婴儿哭声识别算法则成为了哭声识别的一个新问题。
针对噪声环境下婴儿哭声识别鲁棒性不足的问题,文献中给出了很多方法,如能量谱熵端点检测[5]、谱减法、倒谱均值归一化(Cepstrum Mean Normalization,CMN)[6]和VTS特征补偿等。对于不同个体基音不同的问题,文献[7]通过重新设置滤波器的各个带宽提取人为因素倒谱系数(Human Factor Cepstral Coefficients,HFCC)来解决这一问题。文献[8]提出了自适应特征参数AMFCC(Autocorrelation MFCC)来优化这一问题。在文献[9]中,提出了多种特征参数结合的方法,从不同特征参数的不同维度中组选出最优特征参数组合,再使用深度神经网络进行分类,从而提高参数在不同个体之间的鲁棒性。
针对上述的两个问题,本文在传统方法上提出如下两个创新:首先从端点检测出发,使用基于频域的子带谱熵法进行端点检测,增加端点检测在噪声下的鲁棒性,从而提升哭声识别算法的准确性;此外在特征参数的提取上选择了去除基音干扰的平滑Mel频率倒谱系数SMFCC (Smoothing MFCC),该特征可以除去不同婴儿基音频率不同这一因素的干扰,提高了识别算法在不同婴儿之间的鲁棒性;最后使用DTW算法进行匹配,得到了一个在噪声和不同婴儿情况下仍有较好鲁棒性的实时婴儿哭声识别新方案。
1 方案概述
婴儿哭声识别方案由预处理、特征提取、训练模板、模式匹配4部分组成。在预处理阶段,主要对哭声信号进行端点检测、预加重、加窗、分帧傅里叶变换。本文在端点检测中使用子带谱熵法端点检测以增加端点检测在噪声下的鲁棒性。在窗函数上选择动态效果保留更好的汉明窗,在分帧上选择了交叠分段法,帧移选择0.5倍帧长。
特征提取的目的是提取出哭声的特征参数序列,考虑不同婴儿基音频率不同的问题,本文采用SMFCC作为特征参数。其提取方法如下:对预处理后的信号用paul谱包络估计算法得到谱包络;用包络信号代替原信号通过Mel滤波器并取对数能量谱;最后通过DCT变换得到特征参数。
因为哭声信号在时间尺度上不一致,因此选用动态时间规整(DTW)来计算特征序列之间的距离。在给定的训练样本中,通过计算选出与其他序列距离之和最小的km个特征参数序列作为模板。对测试的婴儿哭声特征参数序列,计算其与km个特征序列模板的平均距离,若该值小于阈值,则判断该信号为婴儿哭声信号。
2 哭声信号的预处理
2.1 端点检测
端点检测的目的是获得婴儿哭声信号的有效开始端点和结束端点,传统婴儿哭声识别方案的端点检测多采用时域方法,如短时平均过零率判别,双门限法。但是噪声信号在时域中不容易被单独剥离出来分析,导致时域方法在端点检测中受噪声的影响较大。所以本文使用子带谱熵端点检测法来进行端点检测方法[10],该方法在噪声下有较好的鲁棒性。
子带谱熵端点检测法首先把婴儿哭声信号分帧,假设第m帧的时域哭声信号为x(n,m),计算该帧哭声信号在频率为k频段时的频率特性X(k,m):
(1)
此时第m帧的功率谱总能量E(m)为
(2)
在一帧哭声信号中,该帧信号在某一频段上的分布特性可由该频段的频谱分量在总能量中所占的比例大小反映。因此,第m帧哭声信号在k频段的密度函数P(k,m)就可以表示为
(3)
由于婴儿哭声信号的能量大多集中在500~4500 Hz的频率范围内,而噪声信号由于均匀分布在整个频谱中,所以把500~4500 Hz频率范围外的频段密度函数p(k,m)设置为0。在该信号频谱范围内计算第m帧的谱熵值H(m)为

(4)
根据谱熵做阈值判断已经可以进行端点检测,但此时其鲁棒性容易受谱点污染影响,因此继续把一个帧分成多个子带,再对子带求谱熵。子带的能量计算如下:
(5)
式中,Nb为每一帧的子带个数;l为第l个子带;Eb(l,m)为第m帧中第l个子带的能量。在每一帧中,通过引入一组权值系数w(l,m)重新计算每一帧的谱熵值以弥补谱熵的自然特性:
(6)
最后,设定阈值Ts来判断每一帧的谱熵值是否达到阈值,从而确定该帧是否为有效哭声帧,得到婴儿哭声信号的有效开始端点和结束端点。阈值Ts的确定如式(7)所示:
Ts=μs+αs·δs
(7)
式中,μs和δs分别为环境噪声的谱熵均值和谱熵标准差;αs为一个常数,可以根据具体情况调整。若αs过大,会导致部分婴儿哭声帧被舍弃;若αs过小,会导致部分非婴儿哭声帧被加入。经过多次实验比较,本文实验αs的值设置为2。
2.2 哭声信号的分帧
婴儿的哭声信号是一个非稳态信号,但在短时内可以认为是一个稳态的过程。因此,可以对婴儿哭声信号分帧进行分析。连续分段法和交叠分段法是分帧中常用的方法,交叠分段法在帧与帧之间有过渡,动态特性保留更好。因此采用交叠分段的方法,并在每一帧之间保留50%帧移。
分帧过程通过窗函数实现,即使用一个窗函数平滑地在婴儿啼哭声的信号上滑动。哭声信号是一个连续信号,而汉明窗在动态特性的保留上效果较好[11],且不存在频率泄漏。故使用汉明窗,其频域特性如式(8)所示:
(8)
对加窗后的每一帧的哭声信号进行快速傅里叶变换,得到原始哭声信号每一帧的频率特性。此外,由于婴儿发声系统的特点,哭声在出口腔前会受到口鼻等辐射的影响,从而高频成分会受到抑制,因此需要对婴儿的哭声信号进行预加重,给信号通过一个滤波器,从而让它的高频信号加强,该过程如式(9)所示。其中a的取值在0.9~1.0之间,通常取0.97。
B(z)=1-az-1
(9)
3 特征参数的提取
MFCC参数是哭声识别中常用的参数,它利用了人耳感知的特殊性,目前已经得到广泛的使用。但是MFCC参数没有考虑不同婴儿之间的基音频率差异,婴儿的哭声信号由浊音信号和清音信号组成,哭声能量主要集中在浊音部分,浊音能量主要集中在谐波,谐波频率与婴儿的基音频率密切相关。哭声信号的幅度谱可以表示为基音频率的各次谐波对谱包络的采样。特征参数的提取方案需要在不同婴儿之间具有稳定性,因此本文使用在MFCC参数基础上优化后的SMFCC参数[12]作为特征参数,其提取流程如图1所示。

图1 SMFCC特征参数的提取示意图
SMFCC的提取流程与MFCC的不同之处在于没有把预处理后的哭声信号直接通过Mel滤波器组,而是先从其浊音帧中估计哭声的基音频率,然后通过paul谱包络估计算法[13](Spectral Envelope Estimation Vocoder,SEEVOC)对哭声信号的频率幅度谱进行内插得到包络,并用包络信号代替原信号,进入Mel滤波器组并进行后续处理。
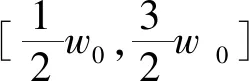
(10)
图2所示是基音频率为465.4 Hz的某一婴儿哭声浊音帧的对数幅度谱和其经过SEEVOC算法后的谱包络。幅度谱中各个峰值所在的频率即各次谐波的频率。由图可知,即使在频率很接近的情况,也很有可能由于某一频率是否在谐波频率的原因导致某一频率上的幅度值变化很大,从而导致不同基音频率的个体哭声特征参数提取有所差异。但是通过SEEVOC谱包络平滑后可以明显减小由于基音频率引起的某一频率的幅度值变化。
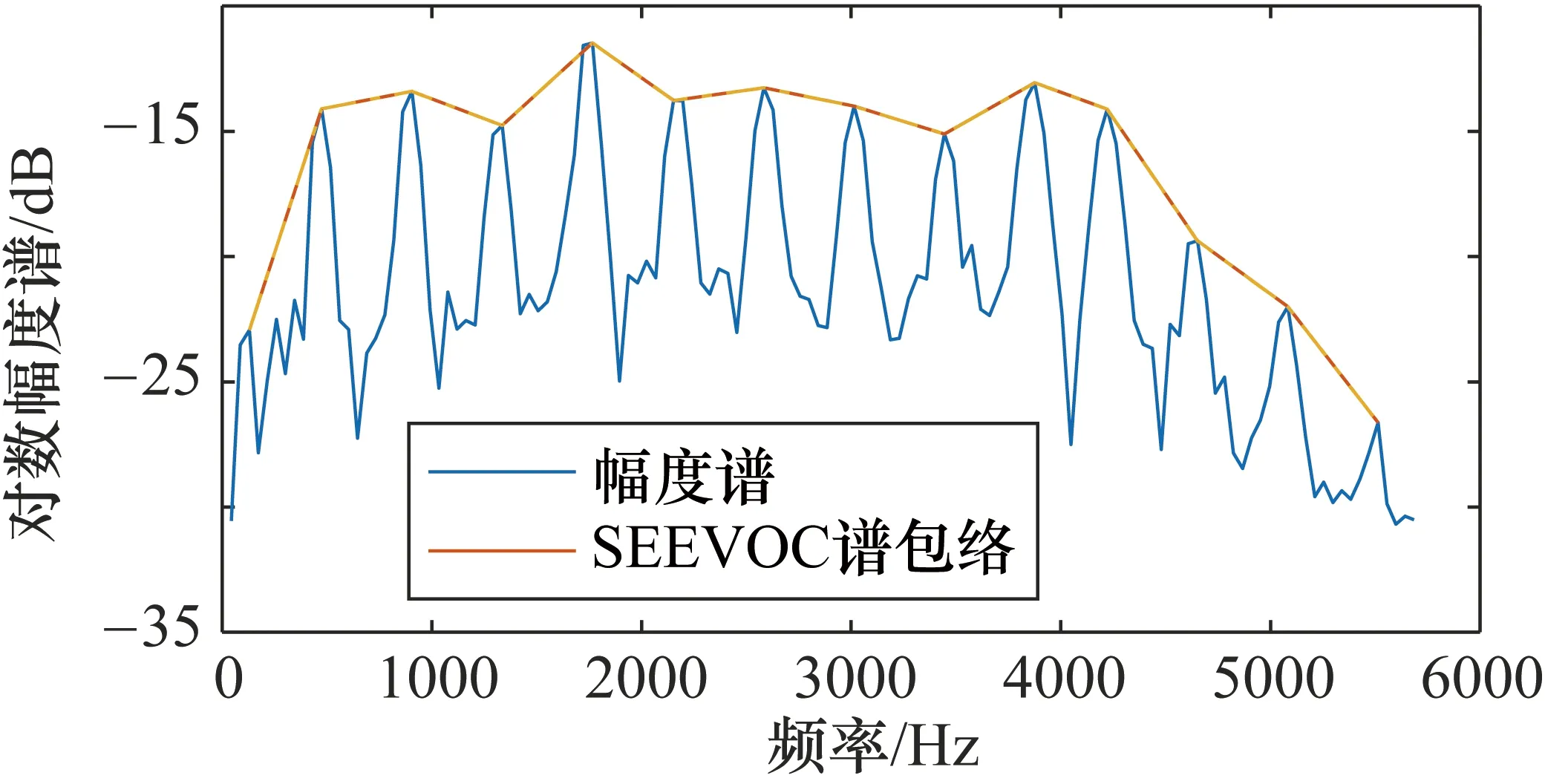
图2 基音频率为465.4 Hz的婴儿哭声帧的对数幅度谱及其SEEVOC算法后的谱包络
Mel滤波器组是一个由一系列三角形序列滤波器组成的滤波器组,其频率特性如图3所示。Mel滤波器组中每一个滤波器的两个截止频率分别是另两个滤波器频率的中心。且在频率越高的地方频带越宽,而在频率低的地方其带宽较窄。该滤波器可以对婴儿的哭声信号进行平滑化,凸显婴儿哭声信号的特征(其中不同颜色的频率谱表示不同中心频率的三角形滤波器)。

图3 Mel滤波器组的频率特性图
将谱包络平滑后的哭声信号通过该滤波器并取对数能量谱。最后通过DCT离散余弦变换得到SMFCC参数:若pj表示经过滤波器后的第j帧信号的对数能量谱,则某一帧的第i维SMFCC参数Ci为
(11)
4 DTW算法
婴儿哭声的时长是未知的,特征参数序列长短也是未知的,因此使用DTW算法作为哭声特征序列模板匹配算法。
DTW算法是一种动态规划算法,对于两个婴儿哭声的特征值序列:q1,q2,…,qn和c1,c2,…,cm,其中qi∈RM,(i=1,2,…,n),cj∈RM,(j=1,2,…,m)。定义向量间的距离为
D(i,j)=‖qi-cj‖2
(12)
定义一个m×n大小的G矩阵,其中每一个元素为到当前为止两个序列之间的距离。然后通过公式(13)递推得到G(n,m)的值,该值即两个序列之间的距离。

(13)
5 实验结果与分析
5.1 实验样本数据库
实验样本数据库由两个数据集组成,分别是婴儿哭声数据集和干扰声音数据集。样本数据来源为公共网站和donate-a-cry corpus婴儿哭声数据库。干扰声音的选择考虑实际场景中可能出现的声音,包括说话声、敲门声、电视声音等,所有样本的采样频率为44.1 kHz,每段样本时长为2 s,其中婴儿哭声样本男女各56份,包括不同年龄的婴儿,干扰声音样本共112份,包括不同种类的干扰声音。
5.2 婴儿哭声信号的端点检测
在不同噪声背景下,对婴儿哭声样本进行子带谱熵法端点检测,噪声选用了不同方差的高斯白噪声,同时使用基于时域的短时平均过零率法进行比较。
图4是同一哭声样本在均值为0、方差为0.0001的高斯白噪声下的两种方案的端点检测结果。其中图中的竖线表示端点检测的结果,哭声信号起始点为4132,结束点为27780。

图4 均值为0、方差为0.0001的白噪声下婴儿哭声的两种端点检测结果
定义α为端点检测起始端点与实际哭声开始点差值的绝对值,β为端点检测结束端点与实际哭声结束点差值的绝对值,λ为实际婴儿哭声采样点长度,则δ=(α+β)/λ的值可以用来综合衡量端点检测的偏移程度。其值越小,说明端点检测的准确率越高。
在图4中,短时平均过零率在起始端点的检测效果较好,但子带谱熵端点检测法在结束端点的检测效果较好。综合考虑开始端点和结束端点,两种方法的δ分别为0.111和0.262,说明子带谱熵法相比于短时平均过零率有更好的抗噪声性能。
表1给出了不同噪声下两种方案的端点检测相对偏移情况δ。可以看出子带谱熵端点检测在给定的不同噪声环境下δ均小于0.15,其抗噪性能较好。

表1 两种端点检测方法在均值为0不同方差的高斯白噪声下的端点检测δ情况
5.3 婴儿哭声信号的特征提取
设定两个哭声样本的基音频率分别为465.4 Hz和541.7 Hz,每一帧的帧长选用1024个采样点,每一帧信号的MFCC和SMFCC参数均选择12维。图5是对两个不同哭声样本的某一浊音帧同时提取的MFCC参数和SMFCC参数的12维数据。在第4,5,7,10,11维中,MFCC参数在两个样本之间的参数差值的绝对值大于SMFCC参数在两个样本之间的参数差值的绝对值。在第1,2,3,6,8,9,12的维度中,MFCC参数在两个样本之间的参数差值的绝对值基本等于SMFCC参数在两个样本之间的参数差值的绝对值。可以看出SMFCC参数对于不同基音频率的婴儿哭声样本有更好的稳定性。
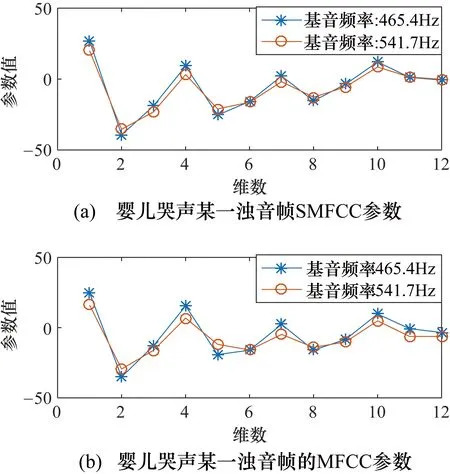
图5 不同基音频率的婴儿哭声样本帧的MFCC参数和SMFCC参数
图6是某一婴儿哭声样本SMFCC参数1维~3维的数值,图中的竖线是端点检测的结果,两条竖线之间是有婴儿哭声的信号帧,两侧是环境信号帧。
从图6中可以看出,在哭声信号帧和环境信号帧上,SMFCC参数的分布特性有很大差异。在样本第1维中,哭声帧的SMFCC参数多分布在15左右,而环境帧的参数多分布在-15左右;同样,第2维、第3维也可以看出SMFCC参数在哭声帧与环境帧中分布特性有所差异。所以使用SMFCC参数能较好地把婴儿哭声和环境声音分离。
5.4 婴儿哭声信号的识别
婴儿哭声识别正确率由对正确样本的接受次数和对非正确样本的拒绝次数之和除以两者样本总数得到。本文使用样本数据库中56段时长约为1 s的婴儿哭声做为训练样本(女婴儿与男婴儿哭声样本各28个)。用DTW算法计算距离。用样本数据库中另外56段婴儿哭声和56段干扰声音作为测试,计算识别正确率。
判别婴儿哭声即判断当前需要识别的特征序列与模板特征序列之间的平均距离是否小于阈值t,判别依据如下式:
(14)
式中,km为婴儿哭声模板数,本文选用km=3;y为当前婴儿哭声的SMFCC特征序列;ui为第i个模板的SMFCC特征序列;t为阈值,本文选用当前模板与其他训练样本平均距离的两倍,dtw(y,ui)即第i个模板的特征序列与当前需识别的特征序列通过动态时间规整后计算的距离。若式(14)成立,则判断为哭声样本。
在没有噪声的环境中,当SMFCC参数选择不同维度时,婴儿哭声识别的准确率如表2所示。可以看出,12维的SMFCC参数有较高的准确率,故选择12位的SMFCC参数作为哭声的特征。

表2 不同维度SMFCC参数下婴儿哭声识别的准确率
在此基础上,改变环境噪声,在均值为0、不同方差的白噪声环境下计算正确率,并与MFCC加短时平均过零率的方法进行比较,匹配算法使用的均为DTW。实验结果如表3所示。其中TP(True Positive)表示该方法在婴儿哭声测试样本中判断正确的数量,TN(True Negative)表示该方法在干扰样本中判断正确的数量。

表3 不同噪声情况不同方法的正确率
由表3可以看出,在无噪声下,本文方法的识别正确率可达83.93%,在噪声环境的干扰下,该算法仍有较高的正确率。相比之下,MFCC加短时平均过零率的婴儿哭声识别方案更易受噪声的影响,且准确率低于本文方法。
6 结束语
本文针对婴儿哭声识别方法在噪声环境下和不同婴儿间鲁棒性不够的问题,把频域端点检测中的子带谱熵法应用到婴儿哭声的端点检测中,使其在有噪声的情况下端点检测准确率有很好的提升,从而提高婴儿哭声识别在噪声下的鲁棒性。除此之外,本文引入SMFCC参数用于解决不同婴儿基音不同的问题,最后使用DTW算法进行模板训练并识别匹配,经实验,该方法获得了较好的效果,噪声环境下婴儿哭声识别正确率达到72%以上,无噪声环境下达到83%以上。

