改进的遗传神经网络算法对花生种子带式清选设备关键作业参数的优化

朱会霞，刘凤超，李彤煜，王辉暖，马 巍

(1.辽宁工业大学管理学院，辽宁 锦州 121001；2.锦州医科大学畜牧兽医学院，辽宁 锦州 121001)

带式种子清选机是基于摩擦分离清选机理设计的种子清选设备，对于大豆、红小豆、绿豆等圆粒型物料中的碎、半豆一次清选精度可达99%以上[1-2]。现有带式清选设备性能参数的优化研究主要针对豆类物料，而花生种子与豆类物理性状差异较大[3-7]，其研究参数较难为花生种子清选提供借鉴。

目前，有关农业机械设备性能参数的优化问题，一般采用试验设计与回归分析的方法建立非线性数学模型，利用方差分析法、单因素效应法等分析试验结果，找出最佳因素水平[8-12]。这种方法是在假设模型基础上进行的回归，而农业机械设备性能参数之间关系复杂，具有很强的非线性和“黑箱”特点，往往难以用确定的函数关系来描述，故此种方法对数学模型选择的要求较高，可能会出现较大估计误差，影响拟合精度。

针对回归模型存在的问题，本文提出基于改进的遗传神经网络优化方法，采用改进的遗传算法彻底取代神经网络中“误差逆传播”过程，形成遗传神经网络算法，用试验数据训练改进的遗传神经网络，并将训练好的遗传神经网络算法用于花生种子带式清选设备关键作业参数的优化。

1 试验材料及方案

由花生种子带式清选设备工作原理可知，花生种子清选质量主要用合格率和带出率两个性能指标来衡量。参考中华人民共和国行业标准种子分级机试验鉴定方法(NY/T366-1999)，合格率H与带出率D的计算公式如下：

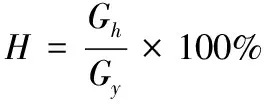
(1)

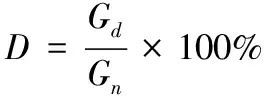
(2)

式中，Gh为成品出料口测定样品中整粒花生质量；Gy为成品出料口测定样品总质量；Gd为废料出口测定样品中整粒花生质量；Gn为废料出料口测定样品总质量；单位均为g。

合格率和带出率两个性能指标主要受纵向倾角A(帆布带与X方向夹角)、横向倾角B(帆布带与Y方向夹角)、帆布带带速C三个关键作业参数的影响，故选取这三个关键作业参数作为试验因素，研究不同参数组合对合格率和带出率的影响，要求合格率最大的同时，带出率最小[13]。供试品种花育33号，运用正交旋转组合试验方法，进行三因素三水平试验，试验因素水平编码情况如表1所示，试验结果如表2所示。

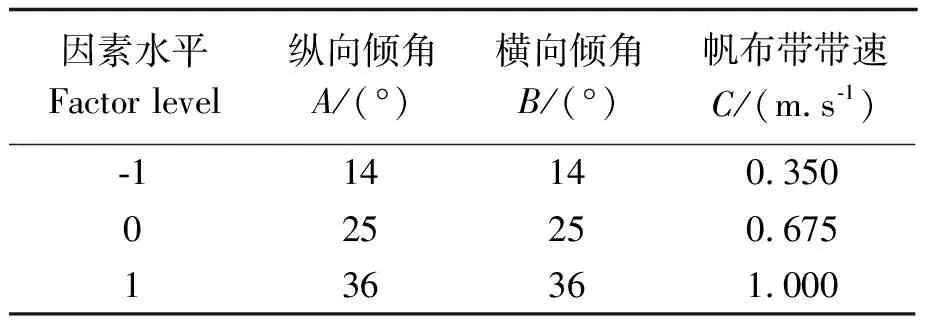
表1 试验因素水平编码表

Note:A,vertical angle;B, lateral angle;C, belt speed.Same as below.

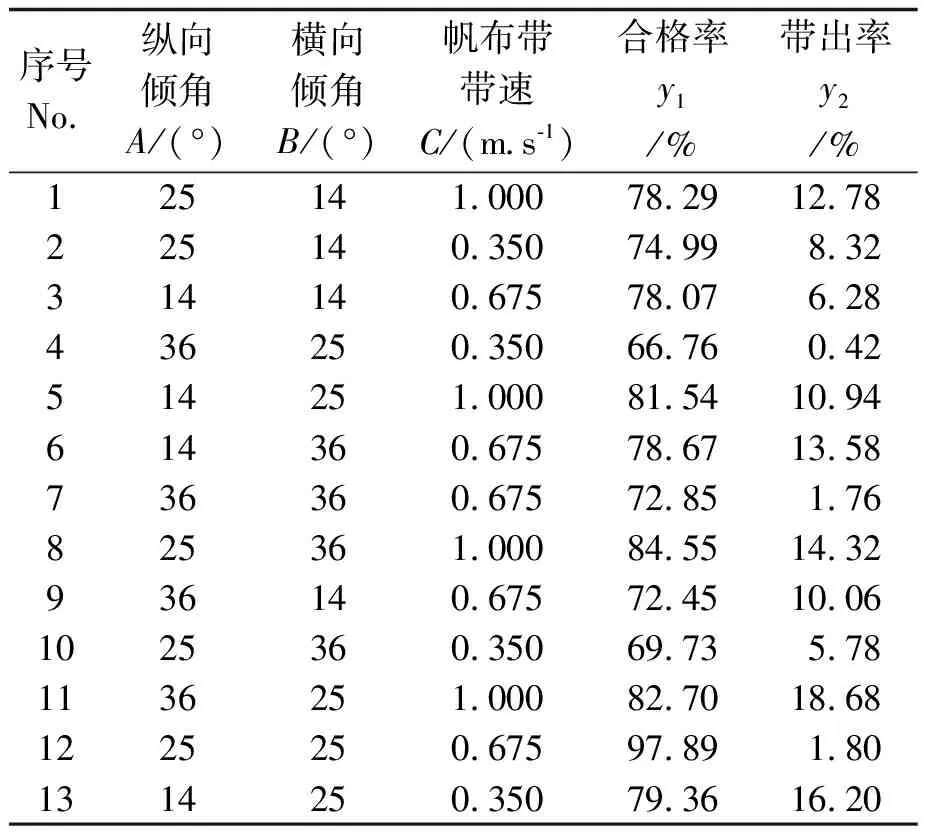
表2 试验方案与结果

Note:y1, qualification rate;y2, entrainment rate.Same as below.

根据表1和表2数据分析，可得合格率H与带出率D回归方程，如式(3)和式(4)所示。

H=96.78-2.86A+0.25B+4.53C-0.05AB+3.44AC+2.88BC-10.28A2-10.98B2-8.90C2

(3)

D=2.34-2.01A-0.25B+3.25C-3.90AB+5.88AC+1.02BC+3.42A2+2.16B2+5.80C2

(4)

2 构建花生种子带式清选设备关键作业参数的遗传神经网络模型

2.1 遗传神经网络结构设计

现已证明三层BP(Back Propagation, BP)神经网络可以逼近任意非线性特征，故采用输入层、隐含层和输出层的三层神经网络构建花生种子带式清选设备关键作业参数网络模型。试验选取纵向倾角A、横向倾角B、帆布带带速C三个变量，故输入层为3个神经元，目标输出量为合格率y1与带出率y2，故输出层为2个神经元，根据隐含层神经元公式计算及经验值确定隐含层神经元结点数为6，即S1～S6，网络结构3-6-2，如图1所示[14-18]。

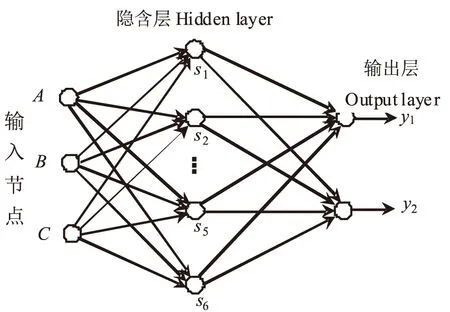
图1 BP神经网络结构图

花生种子带式清选设备关键作业参数与合格率及带出率之间的函数关系如式(5)所示。

Y=F(X)=f[W·f(V·X+θ1)+θ2]

(5)

式中，Y为实际输出；X为试验因素的集合；F(X)为输入与输出之间的关系；f()为神经元的激励函数，各层之间的传递函数为Sigmoid函数；V表示输入层与隐含层之间的权值，θ1表示阈值；W表示隐含层与输出层之间的权值，θ2表示阈值。

2.2 改进的遗传神经网络算法

神经网络算法的学习过程分为信号正传播和误差逆传播两个过程。通过调整权值与阈值空间中的梯度信息使网络收敛，而神经网络算法的误差曲面是一个复杂多元曲面[19-20]，存在学习率难以确定、可能产生振荡等问题，为了克服这些难题，需要摆脱依赖梯度信息调整权值、阈值的方法。而遗传算法最大的优点是搜索不依赖于梯度信息，只需要目标函数是可计算的。因此，本文提出用改进的遗传算法彻底替代神经网络误差逆传播过程，形成遗传神经网络算法，恰好可以解决神经网络算法由于梯度下降引起的难题。

用遗传算法优化神经网络权值和阈值本质是一个无约束问题，基本思想是工作信号正向传播后，得到网络的实际输出，当实际输出信号与给定信号所有神经元的误差能量总和最小时，即为满足训练要求，求得此时最优的连接权值和阈值。但是，神经网络权值和阈值的取值范围不好确定，而遗传算法求解优化问题时，必须预知最优解所在区间，若最优解不在给定的取值范围内，优化问题便求不到真正的最优解，只能求得一个指定区间内的较优解。故采用改进的自适应遗传算法，自适应调整神经网络的权值和阈值，加快网络收敛。

3 花生种子带式清选设备关键作业参数的优化

3.1 数据处理

为了减少输入输出数据之间不同物理意义和不同量纲的影响，防止因净输入值的绝对值过大而使神经元输出饱和，误差不再下降，在训练遗传神经网络前，对输入输出数据进行归一化处理。将数据处理到[a,b]区间的方法如式(6)所示。

(6)

式中xi为样本数据；xi'为尺度变换后的样本数据；xmax，xmin为样本数据xi的最大值和最小值。

考虑到Sigmoid函数在接近0或1时，曲线比较平缓，变化速度非常缓慢，故将样本数据处理到区间[0.1，0.8]之间，加快网络的收敛速度[21]。

误差达到要求时，为了与原始数据拟合，需反归一化变换，公式如式(7)所示。

(7)

式中符号含义与式(6)相同。

3.2 遗传神经网络算法的拟合

选取表2中的试验数据训练遗传神经网络，采用MATLAB R2016b实现上述思想。权值阈值初始区间取值为[-5，5]，种群规模为80个体，交叉概率为0.95，变异概率为0.05，精英个体保留k=4。当遗传神经网络实际输出信号与给定输出信号所有神经元的误差能量总和达到2.2425×10-8时，训练结束，此时权值阈值的结果如下：

输入层和隐含层之间的权值

输入层和隐含层之间的阈值

θ1=[-3.1355 6.6341 1.0773 2.1313 3.0869 -1.6811]T

隐含层和输出层之间的权值

隐含层和输出层之间的阈值

θ2=[0.7084 3.4098]T

将训练好的权值和阈值代入遗传神经网络算法前向计算过程，得到实际输出，将实际输出经反归一化处理后的数据与回归方程得到的数据、试验测量值分别进行拟合，其合格率与带出率拟合精度情况如表3和表4所示。

从表3、表4可知，遗传神经网络的拟合精度明显优于回归方程的拟合精度。合格率的平均相对误差0.0014%，标准差0.0010%，而回归方程的平均相对误差0.0993%，标准差为0.3109%；带出率的平均相对误差0.0414%，标准差0.0793%，而回归方程的平均相对误差为2.3077%，标准差为8.3205%。由此可以得出结论：遗传神经网络算法可使训练误差的目标值达到很高的学习精度，且比较稳定，更接近花生种子带式清选设备试验因素与目标之间的真实情况。

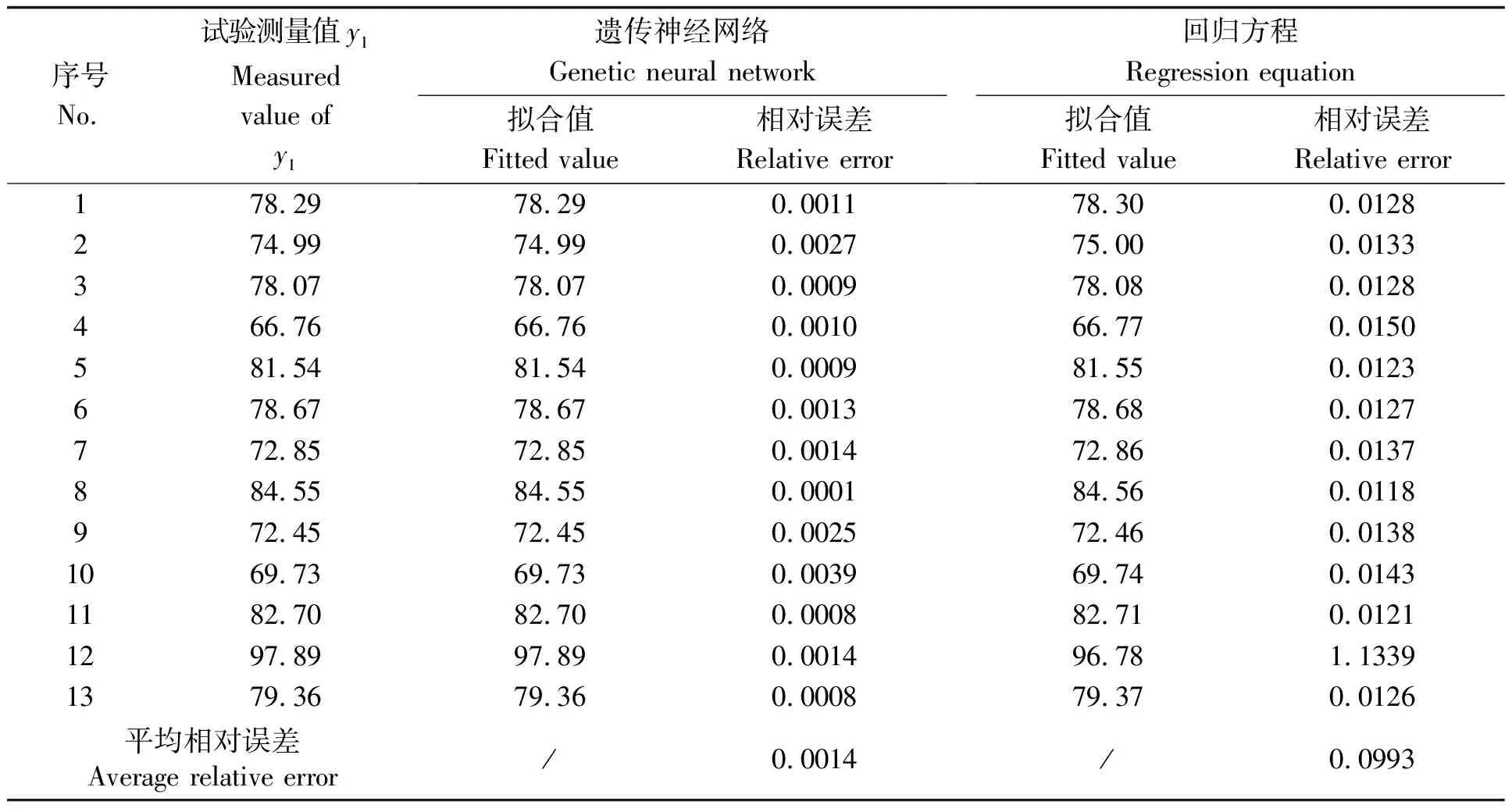
表3 合格率拟合精度情况 (%)

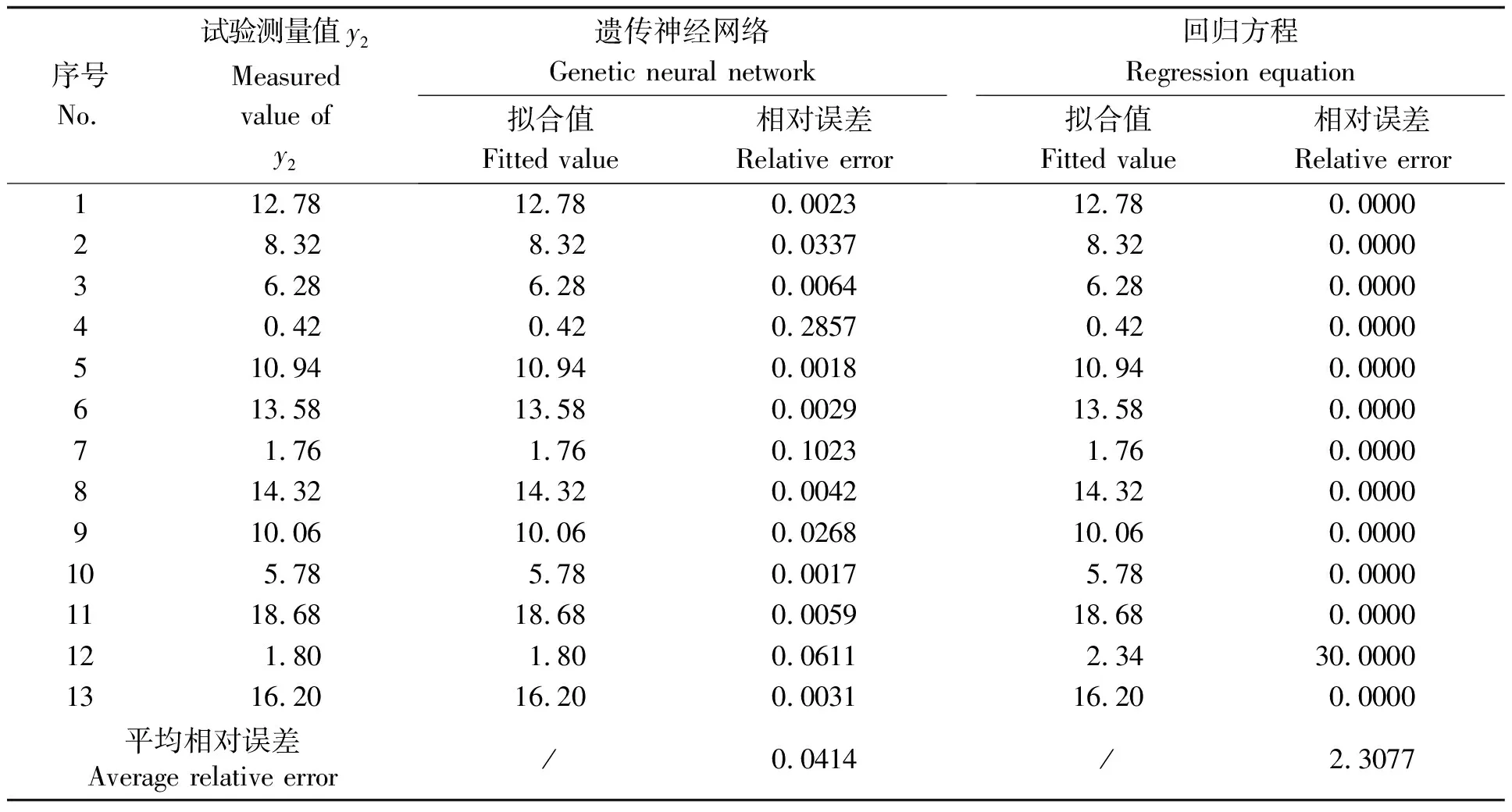
表4 带出率拟合精度情况 (%)

3.3 参数优化

根据花生种子清选工作原理知，需整粒花生种子在帆布带上处于滚动状态，同时半粒花生与帆布带保持相对静止状态，可得花生种子带式清选设备关键作业参数约束条件如式(8)所示：

14 ≤ A ≤ 36

14 ≤ B ≤ 36

(8)

0.35 ≤ C ≤ 1

为了使花生带式清选设备作业情况达到最优，以合格率H最大，同时带出率D最小建立目标函数。考虑合格率与带出率的重要性关系，将目标函数合格率的权重设置为0.6，带出率的权重设置为0.4，优化目标函数如式(9)所示：

minF=0.6 (1-H)+0.4D

(9)

将优化得到的权值和阈值代入遗传神经网络正向输出过程，以式(9)为目标函数，在式(8)的约束条件下，用改进的自适应遗传算法优化花生种子带式清选设备关键作业参数。当算法连续运行1000代结果不变时，结束优化过程。可得：当纵向倾角A=23.66°，横向倾角B=24.26°，帆布带带速C=0.73m/s时，合格率H为98.36%，带出率D为1.85%，花生种子带式清选设备作业性能达到最佳。

4 结 论

(1)针对神经网络模型存在的问题，提出了自适应动态调整神经网络权值阈值的方法，有效克服了神经网络难题，解决了权值和阈值最优解所在区间难以估计的问题。

(2)用改进的自适应遗传算法动态调整神经网络算法的权值阈值，可以使误差能量总和达到2.2425×10-8。与试验数据拟合时，合格率平均相对误差0.0014%，标准差0.0010%，带出率平均相对误差0.0414%，标准差0.0793%。该方法可以得到比回归方法更精确的拟合精度，充分验证了遗传神经网络算法的拟合能力。将训练好的遗传神经网络算法用于花生种子带式清选设备关键作业参数的优化，在纵向倾角A=23.66°，横向倾角B=24.26°，帆布带带速C=0.73m/s时，可使合格率达到98.36%，带出率达到1.85%，实现了花生种子高质量清选。

(3)本研究为花生种子带式清选设备关键作业参数的设定提供了一种新的方法，为同类农业机械设备性能参数优化提供了参考，可减少类似问题的试验次数，降低试验成本，提高参数精度，为实现花生种子加工设备参数的智能化控制提供了一条途径，保证花生种子质量，提高花生种植收益。