非理想信道估计下的全双工MIMO系统的优化研究
傅佳飞,陈芳妮,2,华惊宇 ,徐志江
1(浙江工业大学 信息工程学院,杭州 310023)2(浙江科技学院 信息与电子工程学院,杭州 310023)3(浙江工商大学 信息与电子工程学院,杭州 310018)
1 引 言
全双工(Full-duplex,FD)技术能实现在相同的频带上进行数据的同时双向传输,相比于传统的半双工(Half-duplex,HD)技术,可以显著地增加频谱效率,因此具有更加广阔的发展前景.由于收发同时同频进行,全双工技术面临严重的自干扰(Self Interference,SI)问题.大量工作从理论研究层面[1,2]及硬件实验层面[3,4]提出各种自干扰消除技术,目前这些自干扰消除技术有足够能力可将自干扰抑制至一个较低水平以达到通信要求.
但是,早期的研究结果大都基于理想条件,即接收机已知信道状态信息(Channel State Information,CSI)或不考虑同信道干扰(Co-channel Interference,CCI)、残留自干扰(Residual Self Interference,RSI)等影响.然而,在实际情况中,由于信道瞬时变化及无线设备本身的限制,完整的CSI很难得到,完全消除SI和CCI也是非常困难的.非理想条件下的全双工系统设计已经在一定程度上引起了学者们的关注[5].文献[6]通过使用最大比合并和最优合并的方式对双向全双工系统的遍历容量进行研究,观察信道估计误差带来的影响.文献[7]假设在完美自干扰消除及存在信道估计误差条件下,研究双向全双工MIMO系统的可达速率.非理想信道状态信息条件下的全双工点到点MIMO系统的发射波束成形问题在文献[8]中展开.以上这些研究都只考虑了单用户MIMO双向信道的情形,蜂窝环境下,非理想信道状态信息对FD MIMO多用户系统的影响至今未见.
因此,我们的研究致力于非理想条件下,即存在信道估计误差、残留自干扰和同信道干扰的全双工MIMO蜂窝多用户系统.该系统中,基站工作于全双工模式,而用户设备由于硬件限制工作于半双工模式.无线资源管理方案对于提高系统性能非常重要.文献[9-11]提出联合用户匹配和资源块分配方案来优化全双工系统,但方案中基站和用户都只采用单天线模式,并不符合实际应用.如同文献[12]的动态资源优化分配方案,本文提出了一种联合用户匹配和功率分配的资源优化方案,该方案适用于全双工MIMO蜂窝系统,不仅可以对抗非理想条件带来的性能下降,而且可以保证全双工的优势.
2 系统模型和问题


图1 全双工MIMO蜂窝系统模型Fig.1 FD MIMO cellular system model

(1)
(2)
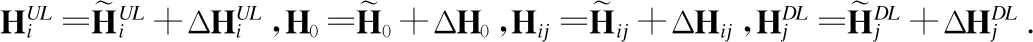
因此,公式(1)和公式(2)可以写成:
(3)
(4)
其中,表达公式(3)和公式(4)中的第二和第四部分是由信道估计误差引起的干扰.第三部分分别是自干扰和同信道干扰.噪声干扰的协方差矩阵表示如下:
(5)
(6)
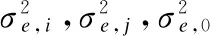
从表达公式(5)和公式(6)我们可以看到,噪声干扰协方差为一个非高斯的复合表达式.假设最糟糕的情形即其服从高斯分布,可以得到传输速率的下界.即,用户对(i,j)的平均速率为:
(7)
因此,系统和速率最大化问题可以表示为:

(8)

为了简洁起见,我们这里只分析上行链路速率,上行链路分析过程相似.我们将Qi进行特征值分解,Qi=UiSi(Ui)H,其中Ui是特征向量的酉矩阵.Si是对角功率分配矩阵,记为Si=diag{si1,si2,...,siN}.
我们可以重写第i个上行链路用户的速率:
(9)
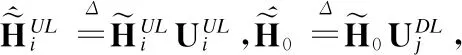
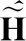

(10)
其中,
3 速率最大化
3.1 用户匹配子问题
由于优化问题P1是NP难问题,需要穷举搜索所有可能的匹配ai,j,而当用户数目很大时,将产生巨大的计算量.为了更好地解决这个问题,我们提出了一个渐近式算法去接近最优解.该算法的主要思想是将原始速率最大化问题分成两个子问题,即用户匹配优化子问题和功率分配优化子问题.
首先假设已获得最优功率分配,P1可被简化为:

(11)
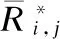
3.2 功率分配子问题
在用户对确定的情形下,我们将处理如下功率分配问题
(12)
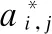
由于信道状态信息误差、自干扰及同信道干扰的同时存在,P3是一个复杂度极高的非凸优化问题.为减少复杂度,我们提出了一种近似,该近似基于当N→∞时MIMO系统容量的渐进形式.文献[13]的研究结果表明,当N非常小时,这种渐进解仍非常接近系统的遍历容量.因此,第i个上行链路用户速率可被近似表示为:
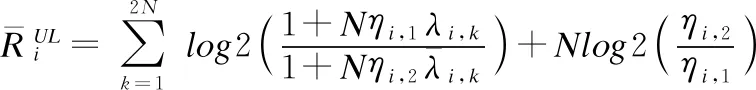
(13)
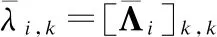
由于参数ηi,1和ηi,2的单调特性,可以使用二分法来求解.
3.3梯度投影算法
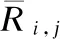
(14)
其中,
(15)
(16)
(17)
(18)
因此,梯度矩阵Gi被记为Gi=diag{gi1,gi2,...,giN}.梯度计算之后,功率分配矩阵被更新为:
(19)
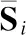
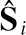
(20)
上述问题为凸优化问题,可以用拉格朗日算法解决.
该梯度投影算法将循坏迭代直到收敛.在第k次迭代中,功率分配更新为:
(21)
(22)
其中,proj[.]即为公式(20)的投影计算.τ(k)和δ(k)是更新步长,可以通过Armijo准则得到.
基于梯度投影的用户匹配及功率分配的联合优化过程可分为如下几步:
1.随机配对用户对ai,j.
3.更新迭代次数k=k+1,根据公式(14)-公式(19)进行梯度计算,根据公式(21)进行梯度投影,根据公式(22)更新功率矩阵操作.
4.检查系统速率的收敛性,若不收敛,算法跳转到步骤3继续迭代;若收敛,则进入步骤5进行用户配对.
5.利用匈牙利算法找到最优的用户匹配对.至此,算法结束.
4 仿真结果
本节,我们通过大量仿真实验来验证提出的算法在全双工MIMO蜂窝系统中的性能.特别地,我们关注不同干扰对系统速率的影响.为了简便起见,我们假设上行用户数和下行用户数相等,即K=J,且所有仿真中步长都统一为τ(k)=τ=0.01,δ(k)=δ=0.5.
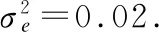
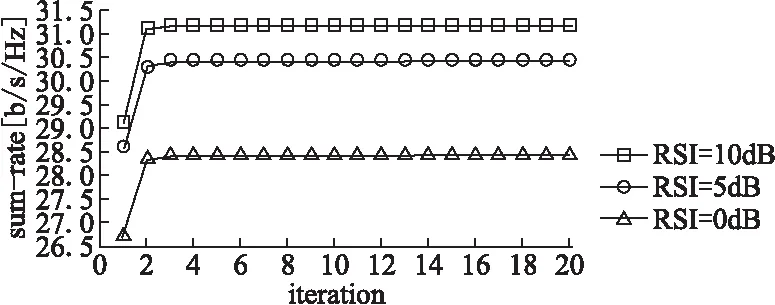
图2 算法收敛性能Fig.2 Convergence of proposed algorithm
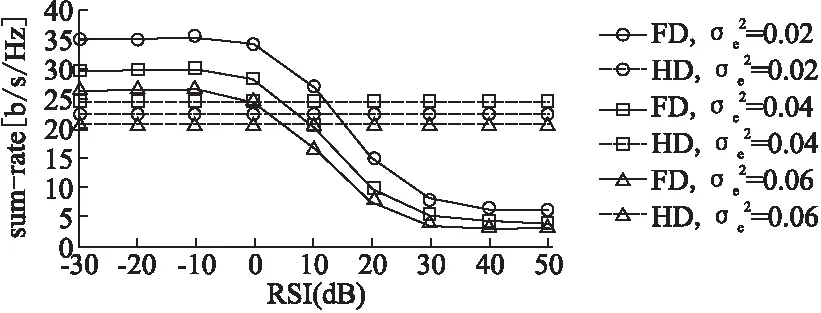
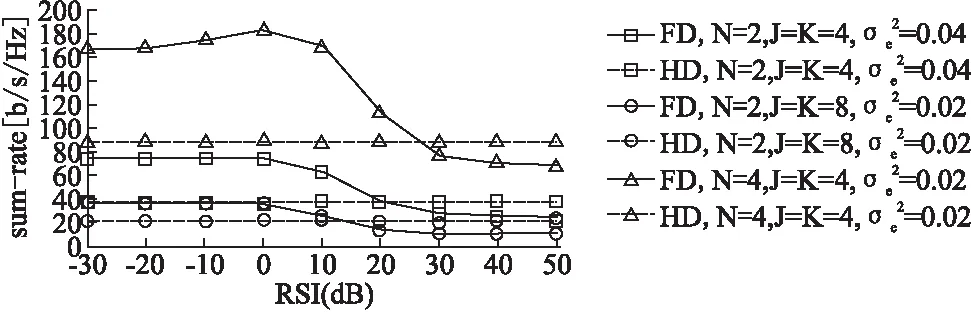
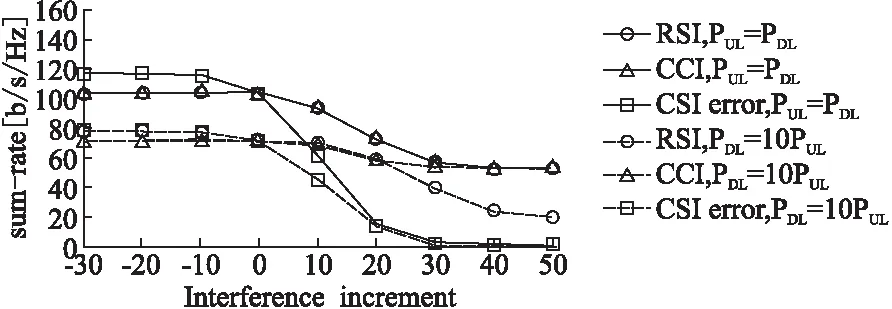
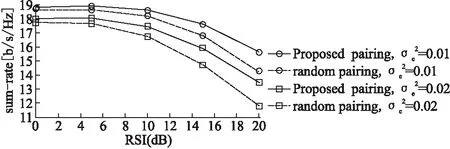
在实际应用中上下行业务可设定速率权重因子来增加系统灵活性,假设上行权重因子为w(0 图3 加权因子对性能影响分析Fig.3 Performance of different weight coefficient 图4和图5分别对比了全双工方案与半双工方案的性能.图4展示了信道估计误差对速率的影响.从图中可以看出,RSI值低时,全双工系统的性能优于半双工系统,然而当RSI值逐渐变高时,全双工的性能优势随之消失.另一个显然而见的现象是半双工系统的性能不随RSI水平的变化而发生变化,这主要是由于半双工系统不存在自干扰.图5展示了FD系统性能随着用户数和天线数的增加而增加,这是由用户分集增益和空间分集增益引起的.图4和图5都表面当CSI误差增加时,FD系统的性能随之下降. 图4 不同CSI下的系统速率性能对比Fig.4 Sum rate performance comparison under different CSI 图5 FD与HD性能比较Fig.5 Performance comparison of FD and HD 不同类型的干扰对全双工MIMO蜂窝系统的影响如图6所示,实线表示上行链路与下行链路具有相同的发送功率,虚线表示下行链路的发送功率是上行链路的十倍.图6中所有曲线在0dB处相交,这是由于当我们分析其中一种干扰对系统性能的影响时,将其余两种干扰值设置为0dB.从图中发现,当上行发送功率等于下行发送功率时,RSI和CCI对系统速率的影响是相同的.此时,CSI对系统速率影响最大,这是由于RSI只存在于上行链路,CCI只存在于下行链路,而CSI同时存在于上下行链路中.当下行链路的发送功率远高于上行链路时,由于上行发送功率低使得CCI相对较低,而下行链路发送功率高使得RSI相对较高,因此RSI对系统总速率的影响就变得更明显.此外,CSI同时存在于上下行链路中,依旧对系统速率产生最严重的影响. 图6 不同的干扰对性能的影响Fig.6 Influence of different interference 图7 不同CSI下的用户配对方式对比Fig.7 Different pairing under different CSI 本文研究非理想条件下即同时存在信道估计误差、残留自干扰和同信道干扰的全双工MIMO蜂窝系统的联合用户匹配和功率分配问题.由于该问题是一个NP难问题,很难得到全局最优解,因此我们提出一种基于分解与梯度投影的渐近式算法来求解.最后,仿真结果表明在不同的干扰情形下,提出的算法具有显著的优越性.当残留自干扰比较小的时候,全双工系统性能优于半双工系统.其次,仿真分析了三种干扰对系统性能的影响,信道估计误差影响最突出,验证了在非理想信道状态信息条件下研究系统优化的必要性.最后仿真结果还表明用户配对算法在速率优化中的重要意义.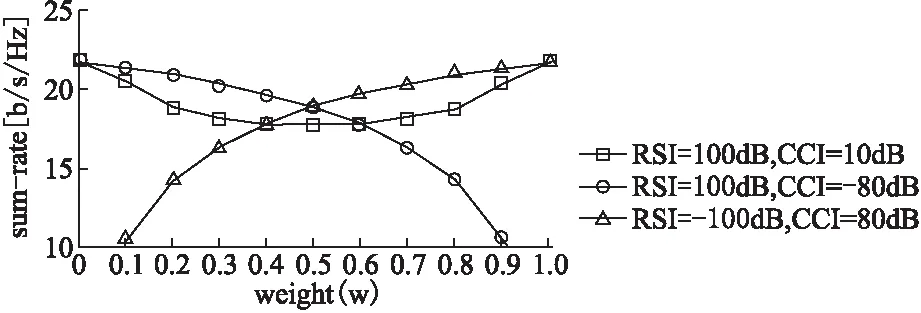

5 总 结

