借助数学模型引领学生建构知识体系

【摘要】本文以《小数的初步认识》教学为例，论述借助数学模型引领小学生构建知识体系的途径，提出运用计数器构建十进制模型、通过不同图形表征强化学生对概念本质的理解、借助数轴模型拓展数系结构等教学建议。

【关键词】数学模型 《小数的初步认识》 小学数学

知识体系

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2020）41-0106-03

《义务教育数学课程标准》（2011年版）指出：模型思想的建立是学生体会和理解数学与外部世界聯系的基本途径。学生学习数学知识的过程，就是不断地抽象、概括、模式化，并在此过程中建立数学模型的过程。教师在教学中将抽象的数学概念与直观的数学模型相结合，揭示概念体系的知识框架，能帮助学生深入理解数学概念的本质，让概念认知结构化。那么，如何用模型理论来指导教学实践呢？笔者结合自己的教学实践，分享在《小数的初步认识》教学中，让学生经历数学概念不断形成和扩张的过程，借助直观、半直观的模型，使学生建构比较清晰的小数概念、完善认知结构的方法。

一、聚焦计数器，建构十进制模型

小数是怎么产生的？巩子坤教授曾在文中提出：“《九章算术》里面用的都是分数，没有出现小数。人类的测量活动，最早产生的也是分数、无理数，而不是小数。小数的出现，要比分数晚得多。小数可以说是人类按照自然数的十进制计数原则创造出来的数，它具有十进制自然数的所有特征，也满足十进制自然数的运算法则，因而用起来十分方便。”计数器作为小数“满十进一”的进制模型，能较好地体现小数和整数的联系，其中小数和整数的本质一样，满十进一，退一当十。笔者尝试利用计数器研究小数，从学生已有的知识经验出发，带领学生经历从整数到小数的产生与形成过程，沟通小数和十进分数之间的联系。

【教学片段1】

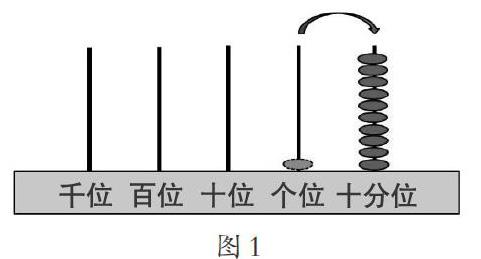
师：你们会在计数器上表示53吗？请在练习纸的计数器上画一画。

生1：我在十位画了5个珠子，个位画了3个珠子。

师：5和3分别表示什么？

生1：5表示5个十，3表示3个一。

师：对，不同的计数单位是有它自己的位置的，个位上的珠子表示几个一，十位上的珠子表示几个十，百位上的珠子表示几个百。

师：1.2是我们今天新认识的数，1.2元表示什么呢？你能在这个计数器上表示1.2吗？请大家动手画一画。

（学生动手操作，全班反馈）

师：谁来给大家介绍一下，你是怎么表示的？

生2：我在个位画了一个珠子，在个位的右边画了两个珠子，表示1.2元。

师：为什么这么画呢？

生2：个位的1个珠子表示1元，还有这个2没有地方放，我就放在了个位的右边。

师：你们有疑问吗？

生3：为什么要放在个位的右边，而不是放在左边呢？

生2：个位的左边是十位、百位，不能放了呀。

生4：1元已经在个位表示了，还剩0.2元，0.2元就是2角，比1元小，不能放在个位的左边，个位的左边是越来越大的计数单位。

生5：0.2元比1元小，原有的个位、十位、百位等这些位置是不可以用的，就需要找一个新的位置。

生6：这个位置要在个位的右边，才能表示比1元小的钱数。

生7：在这个位置上1颗珠子表示0.1元，2颗珠子就表示0.2元。

师：这个新的位置与个位有什么关系呢？

生8：个位的1表示1元，0.2元就表示2角，1元=10角，就是把1元平均分成10份，1份就是0.1元。

师：把1元平均分成10份，这样的1份是[110]元，就是0.1元。如果我在这个位置上再添1颗珠子，是多少？

生9：0.3。

师：继续，再添1颗，是多少？一直继续添……发现了吗？2个0.1是0.2，3个0.1是0.3……10个0.1就是1。

生10：也就是满十进一。

师：个位满十，向十位进一;十位满十，向百位进一;百位满十，向千位进一……看来小数部分跟我们原来的整数部分一样，也是满十进一的。现在我们反过来，从千位往下看。

生11：从千位往下，到百位，是退一作十;从百位往下，到十位，是退一作十;从十位往下，到个位，是退一作十;从个位往下，还是退一作十。

师：从个位退一作十，就是把1再平均分成十份，所以这个数位就是十分位。十分位上的每个珠子表示0.1。

师：通过研究，你们发现这个新位置与之前的数位有什么关系了吗？

生12：我发现在计数器上，越往左表示的数就越大，越往右表示的数就越小。

生13：而且相邻两个数位之间都是十进关系。

生14：十分位与个位之间还应该有一个小数点。

师：对，小数是由“1”进一步细分得到的。小数点把数位顺序表分成两部分，小数点左边是整数部分，小数点右边是小数部分。

以上教学环节，借助计数器表示小数，让学生经历“再创造”的过程。学生通过创造、思考、推理、合作、交流，发现原有的位置已经不够用了，就需要有一个新的位置，而且这个位置要在个位的右边，表示比1元更小的钱数。在寻找这个新位置的过程中，学生借助原有的人民币的知识经验，在不断地探索、对比中认识到，小数是由“1”进一步细分得到的，相邻计数单位间的进率也是十。接着，顺向观察和逆向观察计数器，发现小数和整数一样，从低到高也是“十进”的，从高到低也是“十分”的。学生回顾学习的过程，发现认识整数时，是从“1”开始一个一个地往大数;认识小数，也是从1开始，往小分，从而直观体会整数与小数的内在联系，即小数也适用十进制计数法。

二、不同图形表征，强化对概念本质的理解

《义务教育数学课程标准》（2011年版）提出：“几何直观是指利用图形描述和分析问题。借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路、预测结果。”学生能够凭借图形的直观性，将抽象的数学语言与直观的图形语言有机地结合起来，直观地理解数学知识的本质。借助“几何直观”，引导学生主动建构十进分数与一位小数的联系是认识一位小数的关键。在课堂教学中，教师要尽可能多地提供不同的图形给学生观察、比较、分析和概括，用豐富的模型去揭示概念的本质属性以及外延，帮助学生掌握多维度的小数的概念。

【教学片段2】

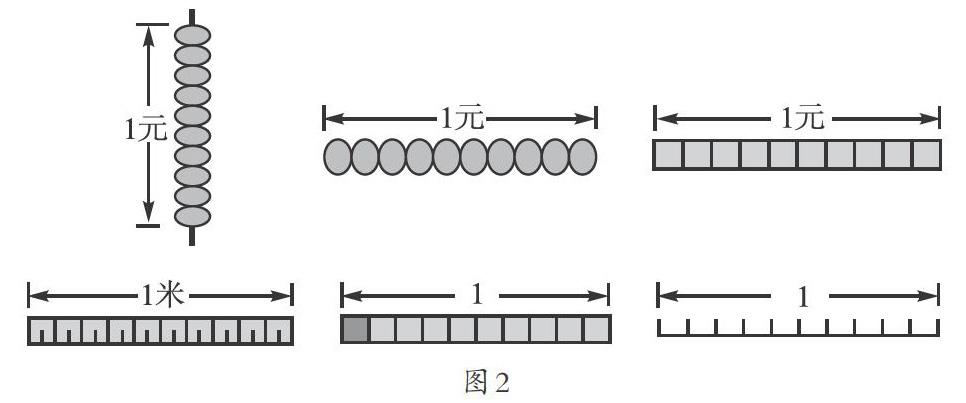
师：看，老师将计数器变换了方向，由竖着摆放变成水平摆放，再变成一个长方形。这个长方形表示1元，你还能找到0.2元、0.5元吗？

生1：只要是其中的任意两份都可以表示0.2元，5份就表示0.5元。

师：为什么呢？

生1：因为每份是1角，2份就是2角，2角就是0.2元。

生2：1元等于10角，把1元平均分成10份，每份就是[110]元，也就是0.1元。

师：用式子表示就是，1角=0.1元。

生3：2份就是0.2元，5份就是0.5元。

师：除了0.2、0.5，你们还能找到其他的小数吗？

（学生在图中寻找其他的小数）

师：看，长方形里的图形继续发生了变化，变成了我们常见的米尺。如果这个长方形表示1米的长度，那么这里的1格又表示多少呢？

生4：1米等于10分米，把1米平均分成10份，每份就是[110]米，表示1分米。

生5：把1米平均分成10份，每份就是[110]米，也就是0.1米，1分米就是0.1米。

师：我们可以用一个式子来表示，1分米=0.1米。2格、3格呢？

生6：有几格就是零点几米，也就是几分米。

师：长方形继续变化。现在它表示1，你们能找到其中的小数吗？

生7：把1平均分成10份，每份就是[110]，也就是0.1，几份就是零点几。

师：如果长方形变成一条线段，这条线段表示1，你还能找到小数吗，你有什么发现？

生8：[110]就是0.1……十分之几就是零点几。

师：仔细观察，图形不同，表示的单位不同，有什么相同的吗？

生9：相同的地方是，都是把1平均分成10份，其中的几份就是十分之几，也就是零点几。

师：对啊，用什么单位并不重要，关键在于我们是否把1平均分成10份，这样才能用小数表示其中的若干份。

以上环节，教师将抽象的数学概念与具体的直观模型结合，先将计数器放倒，变成隐藏有人民币模型的长方形，再由人民币模型变化到米尺模型，然后抽象到长方形、线段图等，让学生在多种图形中找小数，并结合直观图形表达小数的意义，逐步抽象。在此过程中，学生感受到变化的是计量单位，不变的是十进制度量衡，学生对小数的理解由具体的量上升到抽象的数，沟通了小数与分数之间的内在结构关系，抽象小数概念的本质。学生经历概念的形成过程，对概念的理解由具体慢慢过渡到比较理性的认知阶段，经历了从直观数学模型到抽象数学模型的建构过程。

三、借助数轴模型，拓展数系结构

数学的产生和发展有两个途径，第一个是抽象，从生活中提炼而来，第二个是推理。抽象产生了数学，推理发展了数学。两位小数可以在一位小数的认识的基础上，根据前面的经验自然而然地推理出来。数轴是一种介于直观和抽象之间，又非常具有结构化功能的优质数学模型。教师可以创设在数轴上表示小数的活动，让学生感受小数和整数、分数之间的联系。

【教学片段3】

师：我们在线段图上找到了0.2、0.5，那么1.2、6.4、3.58又该怎么表示呢？

生1：在这条线段中找不到这些小数，线段中的小数都是零点几的。

生2：1.2是由数字1和0.2组成的，比1大。可以延长这条线段。

（教师延长线段的长度）

师：线段往箭头方向延长，我们就可以表示更多的数，这样就得到了数轴。现在能找到1.2了吗？

生3：1.2就是在1和2之间。

生4：把1和2之间的线段平均分成10份，第二份对应的就是1.2。

生5：1.2比1多了0.2。

师：6.4可能在哪两个数之间？

生6：6.4比6大，比7小，应该在6和7之间。

生7：把6和7之间的线段平均分成10分，从6数过去4份，就是6.4。

师：在数轴上你还能找到其他的小数吗？

（学生小组互相交流）

师：我们在数轴上找到了这么多的小数，按从左往右的顺序读一读，你有什么发现？

生8：数轴上的数越往右越大;反之，越往左数就越小。

生9：每两个相邻的整数之间都有很多小数。

生10：小数都有顺序地排在相邻的两个整数之间。

生11：在0和1之间的小数都是零点几，在1和2之间的小数都是一点几，在2和3之间的小数都是二点几。

师：对，数轴上任意两个相邻整数之间的一段都可以平均分成10份，其中的每一个点都表示1个小数。小数与整数密密麻麻地排列在数轴上，无论小数还是整数，在数轴上都是越往右，这个数就越大。

师：最后，我们来挑战一下，你能不能在数轴上找到3.58？

生12：3.58应该在3.5和3.6之间。

生13：3.58元就是3元5角8分，1元等于10角，1角等于10分，我们只要把1角再平均分成10份，其中的8份就是8分。

生14：把3.5和3.6之间这一段再平均分成10份，3.5之后再数8小格，就是3.58。

师：你们太厉害了！3.5和3.6之间还可以平均分，其中的每一个点也表示某一个小数，就是两位小数。

学习小数之前，在学生的认知中，数轴上任意两个自然数之间的自然数个数是有限的;认识小数以后，学生发现在数轴上任意两个数之间还有很多很多数，这就是数结构的一种拓展。以上教学片段中，教师引导学生先去寻找1.2，学生在数轴上继续平均分1和2之间的线段找到1.2，对小数的认识从纯小数向带小数扩展;然后寻找6.4，在此过程中学生发现无论小数还是整数，在数轴上都是越往右，数就越大，学生在类比中不断完善数系结构;最后让学生寻找3.58，因为小数也是十进制数，学生再次借助人民币的经验，自主探索出3.5和3.6之间还可以平均分，其中的每一个点也表示某一个两位小数。教师对静态的线段进行设计，把数的分类、数的大小、数的范围、数的无穷性等知识都渗透到动态的数轴中，学生对数轴上“点”的理解更深刻、更到位的同时，将小数纳入数系中，拓展了认知结构。

在小学数学教学中，数学概念的学习是一个重要的内容。教师在课堂教学中要从长远的角度设计教学，带领学生经历数学概念不断形成和扩张的过程，让学生能够借助数学模型深入理解数学概念的本质，把握数学概念知识的基本结构，构建知识体系，更好地发展数学思维能力，发展数学学科核心素养。

作者简介：邓星华（1977— ），女，瑶族，广西贺州人，一级教师，研究方向为小学数学教学。

（责编 刘小瑗）