刚构体系箱梁桥合拢施工阶段水化温度效应分析
庄燕珍
(三明市交通建设集团有限公司,三明 365000)
0 引言
混凝土结构的水化温度效应可能导致结构产生早期裂缝,影响结构的使用性能和耐久性能[1],因此对水化温度应力进行分析并开展相应控制具有重要意义。
大跨径混凝土箱梁由于底板或者腹板尺寸较厚,同样会产生较高的水化温升,箱梁也有较高的开裂可能性。目前针对箱梁0# 块的研究较多, 通过采取温度测试,并进行应力分析, 得出水化温度是早期开裂的主要原因之一,并给出控制内外温差、优化混凝土配合比等相关建议[2-5]。普通箱梁节段尺寸虽然偏小,但在水化热量水平较高的情况下,也可能产生较大的温度应力,箱梁可能出现顶板、腹板或者底板的贯穿裂缝[6-9],箱梁早期温度裂缝问题逐渐得到广泛关注。
刚构体系箱梁桥合拢段也可能产生较高的水化温升效应,由于墩梁固结,升温及降温变形受到纵桥向及横桥向两个方向的约束效应, 可能造成早期开裂现象。本文以某V 型刚构桥为背景工程, 采用温度试验结合有限元分析方法, 对合拢段的水化温度应力开展研究,探明影响规律, 并进行应力控制措施的参数化分析,为裂缝控制提供参考借鉴。
1 工程背景
某连续Y 型刚构桥全长330.12m,位于半径550m 圆曲线上,跨径布置为90.33m+150m+89.79m,上部结构采用单箱单室斜腹板箱梁截面,腹板斜率保持不变。中跨跨中梁高为2.5m,梁高沿纵向按2.5 次抛物线变化,在中墩主梁与Y 构交接处梁高为5.79m。 中墩顶梁段梁高为2.325m,详见图1。
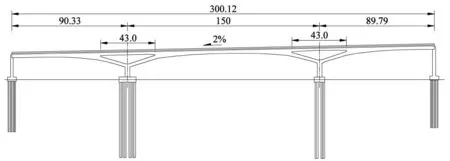
图1 刚构桥总体布置图(单位:m)
箱梁主要尺寸: 顶板厚0.3m; 边跨与中跨底板厚0.47~1.21m,墩顶区域底板厚0.3~0.43m;边跨与中跨腹板厚0.45m,在靠近墩顶位置渐变为0.75m;墩顶腹板厚0.75m;翼缘板长2.06m,厚0.4~0.6m。 典型断面见图2。
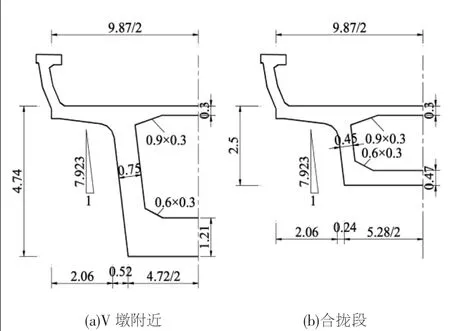
图2 刚构桥断面型式(单位:m)
合拢段浇筑,混凝土为C60 商品混凝土,单方采用P.Ⅱ52.5 级别水泥462kg、砂634kg、碎石1080kg、粉煤灰32kg、矿渣粉42kg、减水剂12.6kg、水137kg。 浇筑时即开展温度测试,测点分别位于合拢段正中断面腹板中心、顶板顶面以及内腔横隔板表面,测试始于浇筑,时长约为7天。
2 计算理论
2.1 水化温度及应力计算原理
温度计算采用瞬态热传导基本方程[10],描述如下:
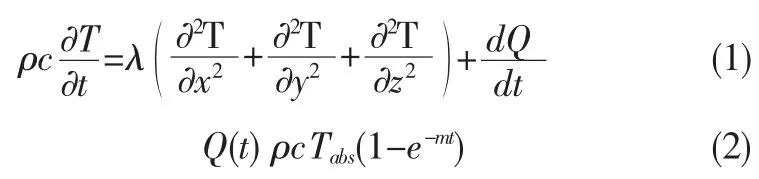
式中:T 为瞬时温度;t 为时间;λ 为导热系数;ρ 为密度;c 为比热容;Q 为生热函数;Tabs为绝热温升;m 为水化速率参数。
早龄期混凝土材料特性具有时变特征, 表现为弹性模量、抗拉强度随时间增长以及徐变效应。 文献[10]提供的弹性模量以及抗拉强度计算公式具有较好的拟合精度,应用范围较广:
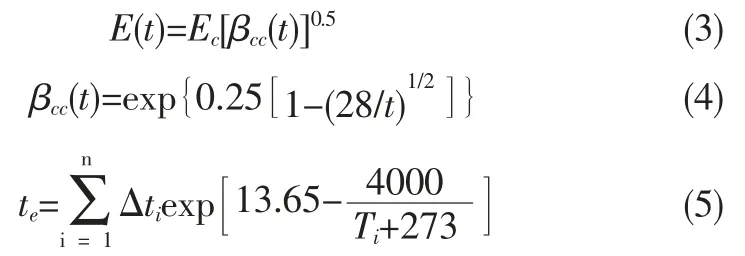
式中,E(t)、ftk(t)为等效龄期t 时刻的弹性模量与抗拉强度,Ec、 ftk分别为标准养护28 天弹性模量与抗拉强度,βcc为材料特性随龄期发展速率参数;te为等效龄期,n 为时间区段的划分数量,Ti为第i 区段的温度,Δti为区段时长。
早龄期徐变效应显著,本文选用文献[1]提供的计算公式进行计算:

式中,C(t,τ)为τ 时刻加载至t 时刻的徐变度,其中C1=0.23/Ec,C1=0.52/Ec。
由于材料时变以及徐变效应复杂, 应力计算采用增量法予以实现,该方法不需要记录应力历史,在有限元软件中易于实现[1]。
2.2 有限元模型及参数选取
采用大型通用有限元软件ANSYS 建立连续两节悬臂段与合拢段的1/4 模型,忽略平曲线,模型纵桥向长度为9m,在悬臂段端部施加弹性支承,在对称面施加对称约束。 弹性支承刚度按照杆系模型中的水平抗推刚度计入,模型如图3 所示。

图3 有限元模型图
温度计算与应力计算采用相同网格模型, 温度计算采用试算方法,通过调整参数取值,使计算值逐渐趋近于实测值。 识别的绝热温升为67.4℃、 水化热释放系数为2.5, 导热系数为2.33W/(m2·℃), 表面对流系数为14W/(m2·℃)、内腔对流系数为8W/(m2·℃)。
3 水化温度效应分析
以温度试验结果为基础, 开展温度拟合以及应力场计算工作,明确温度与温度应力规律。
3.1 温度分析
温度测试结果表明,箱梁具有较高的水化温升效应,最高温度达到77.4℃,相较于平均入模温度28℃,整体升高了约49.4℃。 且水化反应具有较高的速率,浇筑后约1日即达到温峰,拟合得到的水化热释放系数为2.5,也是远高于相关文献的研究结论的[11-12]。 浇筑后第7 日,内部与表面温度基本上下降至环境温度。 拟合结果表明,推定参数组对于温度拟合具有较好的精度, 可以较好地模拟内部温度、表面温度以及内腔温度。 温度计算值与实测值对比如图4 所示。
从温度场的分布来看,合拢段具有整体温度偏高、分布不均匀的情况。 腹板位置温度最高,温度介于73~78℃之间,横隔板次之,温度介于68~73℃之间,外部与大气接触区域温度略低,温度介于43~48℃之间,内表温差达到30℃,如图5 所示。
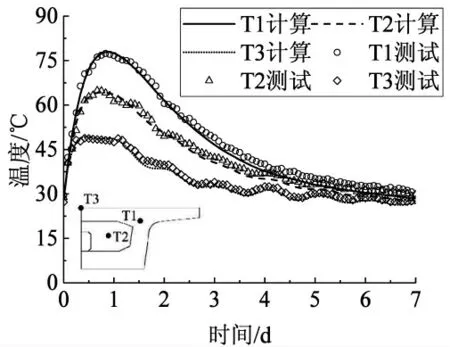
图4 合拢段温度计算值与实测值对比
3.2 应力分析
在较高温升及不均匀温度场的作用下, 极有可能产生较高的受拉应力,对合拢段的应力场进行分析,挑选第4 日、第7 日应力场汇总示于图6。
横向应力分析表明,横隔板第4 日处于受压状态,压应力约为0.8~2MPa,后逐渐转变为拉应力,在第7 日降温后,人孔顶部横隔板全断面拉应力达到2.2~2.5MPa,具有一定的开裂风险。
纵向应力分析表明, 箱梁断面在第4 日处于受压状态,压应力约为0.2~1.4MPa,后逐渐转变为拉应力,腹板与底板拉应力达到1.6~3.3MPa。
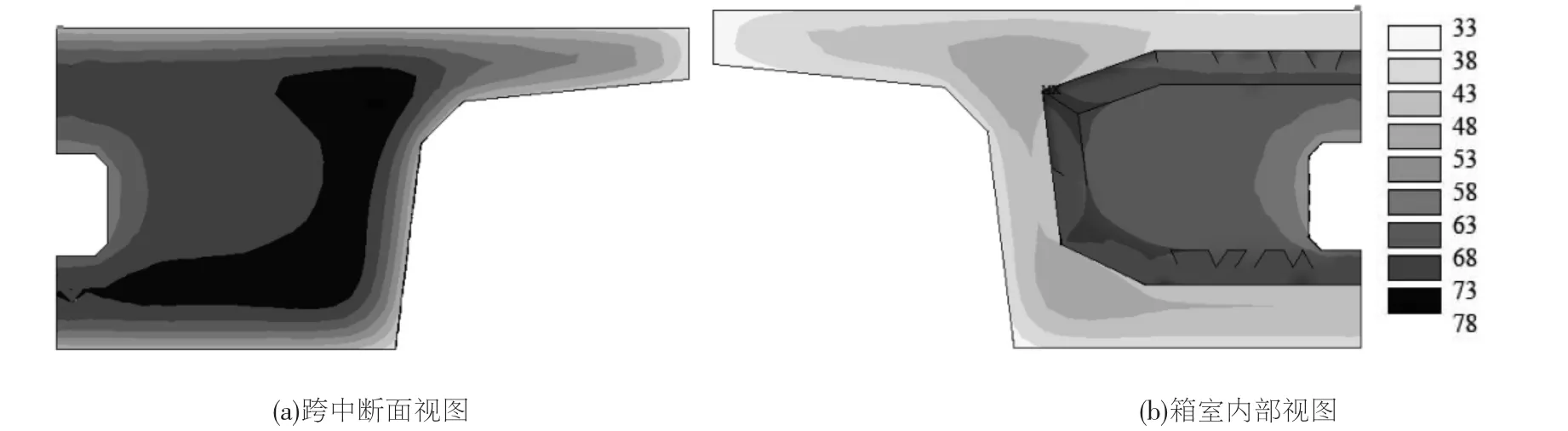
图5 合拢段温峰时刻温度场分布
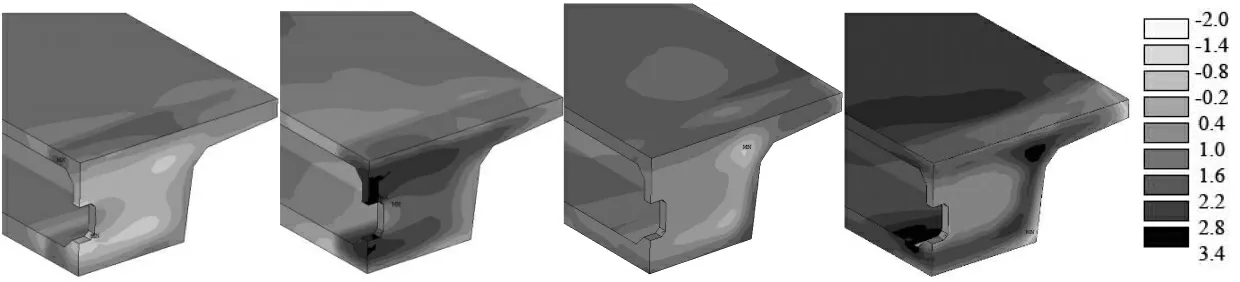
图6 合拢段应力场分布
横向应力与纵向应力分布符合一般水化温度应力的发展趋势,合拢段升温和降温过程中,横向上受已经浇筑节段的约束,纵向上受刚构体系的约束,产生约束应力效应。 前期升温,主要表现为压应力,后期降温,主要表现为拉应力,由于弹性模量逐渐增大,后期产生的拉应力超过前期产生的压应力,故最终应力表现为受拉应力。
此外,箱室内部存在一定的不均匀温度场,底板上缘出现了较高的纵向应力,达到3.6MPa,由于合拢束张拉于第4 日,产生的预压应力达到10.2MPa,可能抵消了该纵向受拉效应,故现场并未发现裂缝产生。
4 参数影响分析
探讨绝热温升、 外表对流系数以及入模温度措施对绝热温升以及应力产生的影响, 为工艺措施制定提供参考。
4.1 对绝热温升的影响
背景工程绝热温升为67.4℃, 外表对流系数为14W/(m2·℃),入模温度为28℃,通过增加或减小参数取值,讨论其对绝热温升产生的影响,计算结果如图7 所示。
计算表明:(1)绝热温升下降或者上升10℃,最高温度下降或上升约7.3~7.4℃;(2)外表对流系数下降以及上升,对最高温度的影响不大,在0.6~1.7℃之间;(3)入模温度下降或者上升5℃,最高温度下降或上升约3.9~4.0℃。
4.2 对横向应力的影响
横向应力提取点为人孔上方横隔板, 绘制不同参数对应的最大横向应力沿时间发展曲线,如图8 所示。
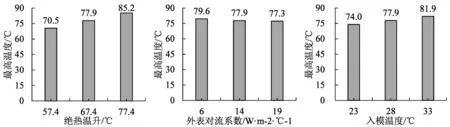
图7 不同参数情况下绝热温升计算值的对比
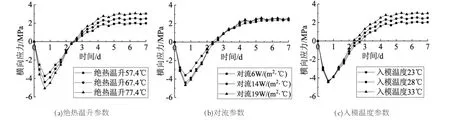
图8 不同参数情况下横向应力计算值的对比
从应力分布可以看出,绝热温升越小,前期的受压应力以及后期的受拉应力也就越小, 绝热温升下降或者上升10℃,最大横向拉应力下降或提高0.5MPa,基本上呈线性关系。
在对流较小时,前期压应力也相对较小,对流系数对最终应力影响不大, 这可能是对流系数对内部温度本身影响较小的缘故。
入模温度对前期的压应力影响较小, 后期随着降温幅度的增大,受拉应力表现出不同的分布趋势,入模温度越小,最大拉应力水平越低,入模温度下降或者上升5℃,最大横向拉应力下降或提高0.5MPa,基本上呈线性关系。
4.3 对纵向应力的影响
纵向应力提取点为底板上方最大应力点, 绘制不同参数对应的最大纵向应力沿时间发展曲线,如图9 所示。
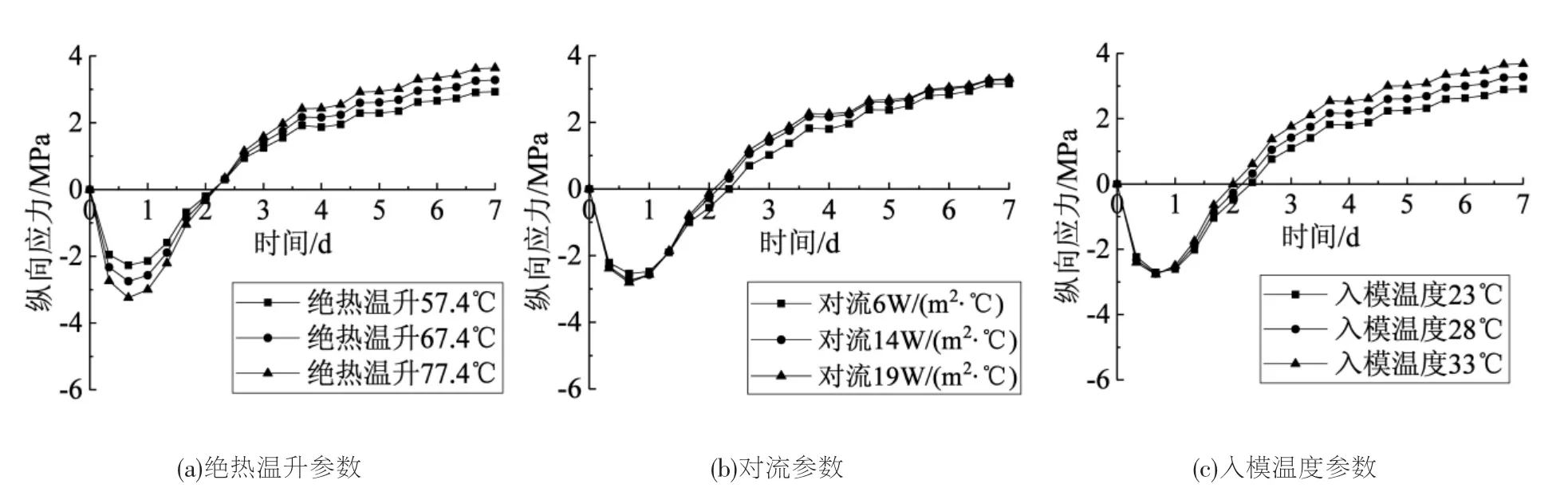
图9 不同参数情况下纵向应力计算值的对比
不同参数对纵向应力产生的影响与对横向应力产生的影响相同,表现在:绝热温升下降或者上升10℃,最大横向拉应力下降或提高0.4MPa; 对流对最终应力影响不大;入模温度下降或者上升5℃,最大横向拉应力下降或提高0.4MPa。
5 结语
通过对某刚构桥梁合拢段开展温度测试, 结合有限元分析方法,对温度及温度应力开展研究,结果表明:
(1)合拢段内部最高温度可达到77.4℃,具有较高的温升效应,且温度上升速率较快,在1 天内即可到达最高温度;
(2)合拢段横向受已浇筑节段约束,纵向受刚构体系约束,在水化温度影响下,横隔板内部可能产生较大的横向受拉应力,底板可能产生较大的纵向受拉应力;
(3)增加或者减小绝热温升、提高或者降低入模温度,对内部最高温度影响显著,改变表面对流系数,对内部最高温影响较小;
(4)减小绝热温升、降低入模温度可以有效改善横向受拉应力和纵向受拉应力, 改变表面对流系数对受拉应力的改善作用较小。
综上所述, 刚构体系箱梁桥合拢段具有较高的水化温升,可能导致早期开裂现象,可通过减小绝热温升、降低入模温度减小受拉应力。 本文结论可以为质量控制提供参考借鉴。

