大跨斜拉桥钢箱梁局部应力分析及加固措施
董建松
(福建省交通建设质量安全监督局,福州 350001)
1 引言
自20 世纪40 年代问世以来,正交异性钢桥面OSD(Orthotropic Steel Deck) 已经成为现代钢桥的重要构件形式和主要标志[1]。由于具有自重轻、承载力高、适用范围广等突出优点, 正交异性钢桥面板已经成为大跨度桥梁的首选桥面板结构,在中等跨度桥梁、景观桥梁、梁高受到严格限制的城市和市政桥梁、 既有桥梁加固工程等条件下同样具有较强的竞争力。 目前世界各国已建成的采用正交异性钢桥面板的各类桥梁已超过1500 座,中国正在运营和规划中的该类型桥梁数量已达200 余座, 该结构的推广和应用大大推动了桥梁工程向大跨、 重载和结构造型多样化等方向发展[2]。
正交异性钢箱梁主要由顶板、纵肋和横隔板组成,受力复杂,容易产生应力集中现象[3-4]。正交异性钢箱梁在车辆长期荷载作用下,在顶板、横隔板以及纵肋连接的关键部位易出现疲劳损坏,从而影响桥梁的正常使用寿命。因此, 建立合理的计算模型分析正交异性钢箱梁的受力状态是十分必要的。
2 工程概况
长门特大桥是项目中重要的控制性工程, 主桥全长848m,结构形式为(35+44+66)m+550m+(66+44+35)m 双塔双索面混合梁斜拉桥,如图1 所示。边跨采用混凝土箱梁中跨采用钢箱梁,钢与混凝土分界线距索塔中心线24m。主桥结构为七跨对称混合梁斜拉桥, 边跨及主跨索塔附近为混凝土主梁,中跨大部分为钢主梁。主梁中跨采用封闭扁平流线型钢箱梁、边跨采用混凝土箱梁,为单箱四室箱梁,双向预应力结构。桥梁全宽38.5m(包括两侧斜拉索锚固区及风嘴),梁高3.2m,至索塔区缩窄为35.5m。

图1 长门特大桥主桥立面布置图
3 计算模型
3.1 有限元模型建立
首先采用桥梁结构专用程序MIDAS Civil 对大桥进行整体计算。整体分析有限元模型中,活载计算时斜拉索采用桁架单元模拟,加劲梁及塔、墩等构件均采用空间梁单元模拟,主梁与拉索间的连接采用刚臂的方式实现。长门特大桥整体分析有限元模型如图2 所示。 首先利用MIDAS 软件分析得到桥梁整体模型的应力和位移,然后利用abaqus 软件建立桥梁的子结构模型如图3 所示,单元类型采用壳单元,模型共有72510 个单元,92053 个结点。 然后将MIDAS 计算得到的位移作为abaqus 子结构的边界条件,进行桥梁局部应力有限元分析。

图2 整体有限元模型

图3 abaqus 子结构有限元模型
3.2 计算参数
混凝土箱梁及主塔: 主塔及混凝土主梁采用C55 混凝土,容重γ=26kN/m3;弹性模量EC=3.55×104MPa。 钢箱梁弹性模量为2.06×108kN/m2,泊松比0.3,斜拉索抗拉强度为1770MPa,弹性模量1.95×105MPa。
3.3 荷载及边界条件
进行整体模型分析时,斜拉索与主塔及主梁固结。塔梁固结, 主梁与辅助墩及过渡墩顶支座采用一般支座约束模拟。进行局部详细应力分析时,将整体模型计算得到的位移作为子模型的边界条件。
本模型仅考虑在车辆荷载作用下钢箱梁的位移情况, 由于Midas Civil 软件在分析车辆荷载结果时自动依据目标节点位移的影响线的最不利位置来排布车辆荷载,仅能输出目标节点位移的最大或最小值,而不能同时输出在目标节点最不利情况下其他节点的位移情况。 故而需要利用软件中 “将移动荷载工况转化为静力荷载工况”的功能,将某一结点位移最不利情况下所受的车辆荷载转化为静力荷载, 得到在桥身受相同荷载下各节点的位移。 本文取桥梁跨中节点位移的最不利情况所受的荷载作为分析的荷载,受力情况如图4 所示:

图4 模型加载示意图
4 计算结果与分析
首先利用Midas 软件对桥梁进行整体受力分析,得到了桥梁的内力和变形。 图5 和图6 分别给出了桥梁的整体变形图和桥面的挠度曲线。从图5 可以看出,桥梁整体模型中,桥面和立柱的变形较大。由于立柱两侧拉锁受力不对称,导致两边立柱产生向内侧的变形。从桥面的挠曲线图可以看出, 从支座到跨中桥梁的竖向位移基本呈线性变化,整个桥梁的最大竖向位移发生在跨中位置,最大竖向位移为0.615m。
将上述Midas 计算位移结果作为abaqus 子模型的边界条件,对桥梁局部进行详细应力分析。图7 给出了桥面的mises 应力分布,从图中可以看出,桥面的最大应力发生在分布、荷载作用线上,最大应力达86.1MPa。 图8 给出了轮轴线上的mises 应力随纵向位置的变化关系,从计算结果可以看出, 荷载作用线与横隔板交界处应力出现突变,桥面最大应力发生在横隔板外侧。

图5 桥梁整体边形图

图6 桥面的挠度曲线

图7 钢桥面板mises 应力分布图

图8 钢桥面板mises 应力随纵向位置变化关系
图9 给出了中间横隔板和外侧横隔板的mises 应力分布,从图中可以看出,外侧横隔板的最大应力发生在下方拐角处与底板接触部位, 最大应力为13.9MPa,横隔板中间部位应力较小,最小应力为0.18MPa;内侧横隔板的最大应力发生在圆孔附近,最大应力为9.8MPa,横隔板两侧应力较小,最小应力值为0.39MPa。 横隔板缺口处是一个关键部位, 因此对缺口处重新建立局部有限元模型, 对车辆经过时车轮集中荷载作用进行模拟,得到了缺口处的应力分布如图9 所示,会产生明显的应力集中现象。

图9 横隔板mises 应力分布图
图10 给出了内侧横隔板的正应变分布图,从图中可以看出,横隔板最大变形发生在与U 肋接触部位,会产生拉伸变形,最大值为29.6×10-6;在开口附近会产生较大的压缩变形,最大应变值为21.2×10-6。 图11 给出了纵肋顶板正应变随纵向位置变化图,最大正应变为压应变,发生在横隔板外侧,最大值为307×10-6;在横隔板内侧产生最大拉应变,最大拉应变值为-94.6×10-6。

图10 内侧横隔板局正应变

图11 纵肋顶部应变分布

图12 纵肋mises 应力分布
图12 给出了集中荷载附近纵肋的mises 应力分布,从计算结果个可以看出, 纵肋的最大应力发生在与分布荷载作用线重合区域, 图中给出了u 肋mises 应力随纵向位置的变化关系。 图13(a)是纵肋底部应力随纵向位置变化规律,从图中可以看出,U 肋底部最大应力发生在与内侧横隔板接触部位,最大应力为33.5MPa,最小应力发生在集中力作用位置,最小应力值为1.6MPa。 图13(b)给出的是纵肋与桥面接触位置mises 应力随纵向位置变化关系, 从图中可以看出,u 肋顶部的最大mises 应力发生在u 肋与横隔板接触部位,最大应力达72.8MPa。 在集中力作用点附近出现最小应力,最小应力值为4.78MPa。
5 加固措施
由于钢箱梁受力复杂,容易产生疲劳破坏,从而影响车辆的安全,带来较大的经济损失,因此有必要研究钢箱梁的加固方法进行研究总结。 目前国内外对钢箱梁加固方法有了一定的研究成果[5-7],结合本研究前面得到的静力学计算结果,对钢箱梁提出如下加固措施:
(1)通过静力分析可以看出,桥面与横隔板接触处产生最大应力达86.1MPa。 因此为了使应力分散,减小应力集中现象,可以适当减小横隔板间距,并增加横隔板附近区域桥面的厚度。

图13(a)纵肋底部mises 应力随纵向位置变化关系
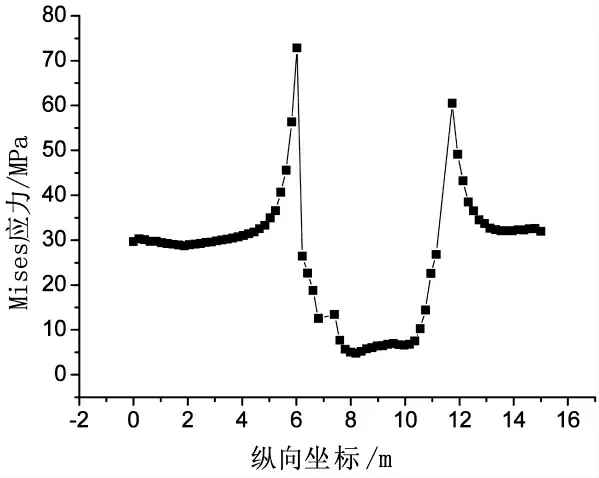
图13(b)纵肋顶部mises 应力随纵向位置变化关系
(2)横隔板人孔附近产生较大的应力和应变,因此很容易在此区域产生疲劳破坏, 为了改善横隔板的力学性能,可以在人孔附近加桁架支撑,以减小人孔附近的应力和变形。
(3) 由于横隔板缺口处出现明显的应力集中现象,因此可以考虑对缺口采用加强钢板补强, 钢板与横隔板之间通过高强度螺栓连接。
6 结语
建立了长门特大桥全桥模型以及子结构模型, 分析了在车辆荷载作用下桥的局部详细应力, 得到了桥的最大应力发生部位, 该计算结果可以为桥梁的疲劳分析和加固方案提供一定的依据; 对桥梁的加固措施进行了总结,为桥梁的维护提供了参考。

