Research on Robust Cooperative Dual Equilibrium with Ellipsoidal Asymmetric Strategy Uncertainty

LUO Gui-Mei

(School of Financial Mathematics and Statistics,Guangdong University of Finance,Guangzhou,Guangdong, 510521, P.R. China)

Abstract: In this paper, we investigate robust cooperative dual equilibria with two players in which each player minimizes the opponent’s cost and can not evaluate his own strategy while may estimate an asymmetric bounded set of the mixed strategy. Using dual theory and robust optimization technique, we obtain a result that the counterpart of the primitive uncertainty with ellipsoidal norm for each player can be formulated as a second-order cone programming (SOCP) and solving the corresponding equilibrium can be converted to solving a second-order cone complementarity problem (SOCCP). Then we present a numerical experiment to illustrate the behavior of robust cooperative dual equilibrium.

Key words:Robust cooperative dual equilibrium;Asymmetric strategy uncertainty;SOCP;SOCCP

§1. Introduction

Bimatrix game is the formal study of decision-making where two players make choices that potentially affect the interests of his opponent. In[14-15],John Nash first introduced the notion of an equilibrium (Nash equilibrium) of a non-cooperate, simultaneous-move, one-shot, finite games with complete information. However, in real-world, game-theoretic situations, players are often uncertain of the structure of the game, such as player’s own strategies [16, 18]. When each player’s strategy set depends on the other players’ strategies and at the same time, each player acts in his own selfish interest, Facchinei et al. [8-9]and Pang etc. Fukushima [17]studied general Nash equilibrium using quasi-variational inequalities or variational inequalities. In[1], Aghassi and Bertsimas introduced robust optimization equilibria and established existence theorems for this equilibria. Robust optimization is emerging as a leading methodology to address optimization problems under uncertainty. Ben-Tal and Nemirovski [2-3, 5, 7]and other researchers investigated the robust counterparts under different uncertainty sets. Wiesemann etc. [19]introduced standardized ambiguity sets which contain all probably distributions with prescribed conic representable confidence sets and with mean values residing on an affine manifold. Bertsimas et al. [4]proposed a novel schema for utilizing data to construct uncertainty sets for robust optimization using statistical hypothesis tests. In this paper, we consider a cooperative dual equilibrium (DE) [6]with uncertainty in which each player unselfishly responds to the DE strategy for the other player so as to minimize the cost of the other player.

In what follows, from the structure of strategy uncertainty, we consider a two-person game,in which each player attempts to minimize his opponent’s cost where each opponent’s strategy belongs to a mixed strategies set and his own strategy is uncertain while can be estimated to be included in an asymmetric closed and bounded set. In this situation, the model essentially reduces to the following programming:

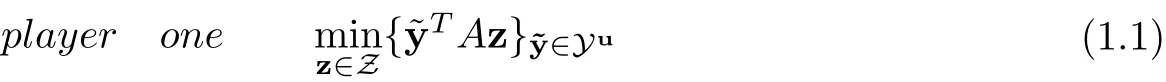
and

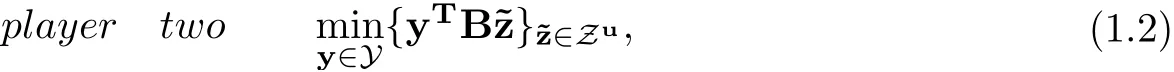
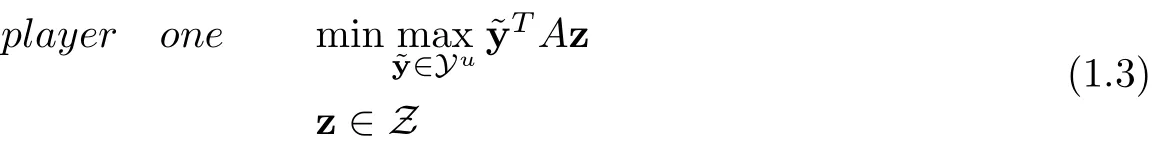
and

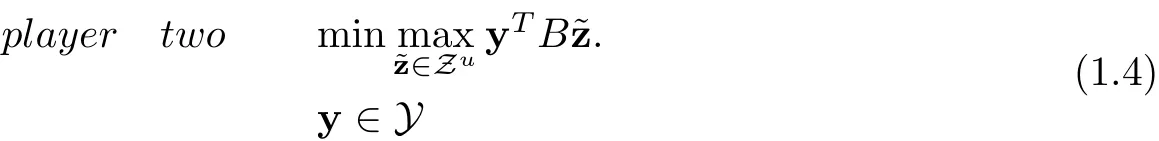
A pair of strategies (z,y) is called a robust cooperative dual equilibrium for problems (1.1) and(1.2) if z is the optimal solution to (1.3) and y is the optimal solution to (1.4) simultaneously.Accordingly,(1.3)and(1.4)are called robust counterparts of(1.1)and(1.2). However,problems(1.3) and (1.4) are generally semi-infinite programming problems and usually computationally intractable. How to deal with an uncertainty set is very important in the solution to these problems. In what follows, we assume that the uncertain strategy sets can be estimated at some asymmetric bounded sets. When the elements of the mixed strategy sets are ellipsoidal uncertainty, the robust counterparts for each player can be formulated as a second-order cone programming and the corresponding robust cooperative dual optimization equilibrium can be converted to a second-order cone complementarity problem (SOCCP) [5, 11]as follows:

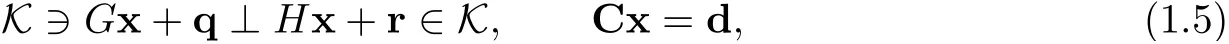
where K is a ς-dimensional closed convex cone defined by K=Kς1×Kς2×···×Kςmwith ςj−dimensional second-order cones Kςj={(x1,x2)∈and ς =ς1+···+ςm,G, H ∈, C ∈andd∈The major contributions of the paper are as follows.

(a) The equilibrium is based on the viewpoint of cooperation which is different from the traditional non-cooperative case such as [12].

(b) The asymmetric uncertain set better captures the essence of the underlying random variables comparing to symmetric uncertainty.

(c) Using robust technique, the intractable primitive problem including asymmetric uncertainty for each player can be converted to a computable SOCP. Then the dual equilibrium of cooperation between two players can be formulated as a SOCCP defined in (1.5). From this point, the work is an extension of that in [5]where the asymmetric uncertainty only in unilateral activities not in bimatrix games was considered. At the same time, it generalizes the work in [12]in which only symmetric games was investigated.

The paper is organized as follows. Section 2 investigates the robust counterpart and the corresponding equilibrium when each player can be certain of his own cost matrix and can not estimate his own’s strategies exactly while the strategies are estimated to be contained in an asymmetric ellipsoidal uncertain set. Some numerical experiments are presented in Section 3.

§2. Asymmetric Ellipsoidal Uncertainty in Players Own Strategy

In this section,we focus our attention on the tractability of problems(1.3)and(1.4). To this end, it is necessary to deal with the inner optimization problems which rely on the structures of Yuand Zurespectively. In what follows, we investigate a general uncertainty set, namely,asymmetric ellipsoidal uncertainty. We first consider (1.3). For each ˜y∈Yu, we let

whereydenotes the nominal value ofl = 1,··· ,L are random vectors,yl∈Rnare known directions of data perturbation for,l = 1,··· ,L, L may be small, modeling situations involving a small collection of primitive uncertainties, or large, potentially as large as the number of entries in the data. Let= max{0,= max{0,−. ThenUnder these assumptions, the asymmetric uncertain set (2.1) under l2-norm can be written as

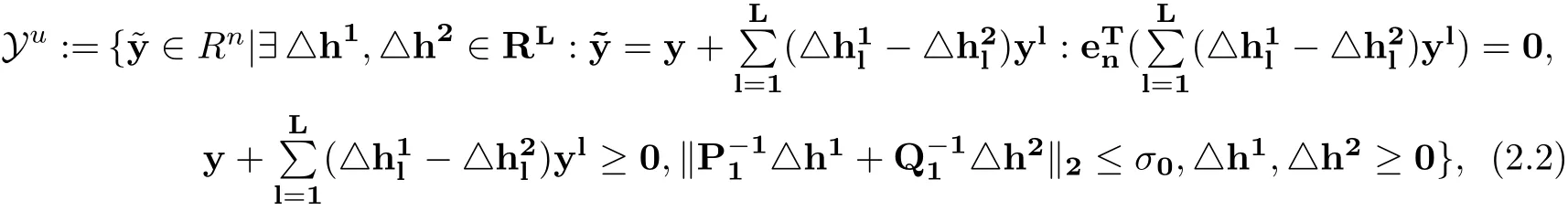
where P1= diag(p11,··· ,p1L) and Q1= diag(q11,··· ,q1L) with p1l,q1l> 0,l = 1,··· ,L are forward and backward deviation related to the random variable △hj,j=1,2,σ0is a parameter controlling the tradeoff between robustness and optimality. The conditionsandensureto be a mixed strategy.

It is easy to obtain that whenis given as (2.2), then the robust counterpart of (1.1) can be formulated as an SOCP. To this end, we first introduce the following lemma.

Lemma 2.1(Chen, Sim and Sun [5]) Let

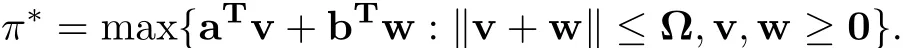
Then π∗=wheret=(t1,...,tN1)T, tj=max{aj,bj,0},j ∈N1.

Theorem 2.1If player one’s strategy set is given as (2.2), then the robust counterpart of (1.1) can be formulated as an SOCP over varies (z,α,r,γ,f) ∈as follows.

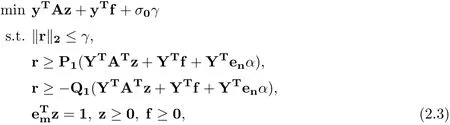
where Y =(y1y2···yL)∈denotes the matric of perturbation directions.

ProofFor the worst case, (1.1)can be expressed as(1.3). When Yuis given as(2.2), the inner optimization problem of (1.3) can be written as

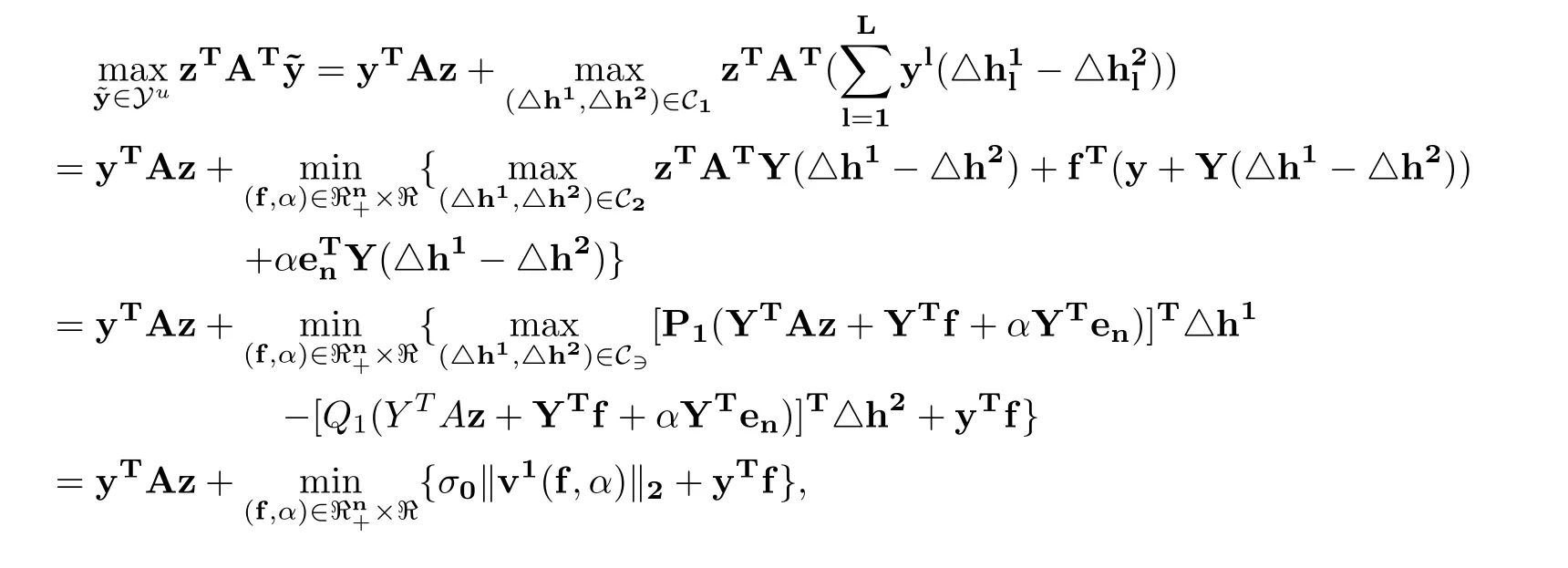
where

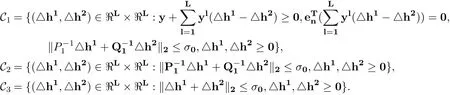
Under some mild condition, such as the existence of Slater points [10], the zero duality gap is guaranteed by strong conic duality theorem, and the third equality comes from direct transformation of vectorsrespectively and the last equality follows from Lemma 2.1 and

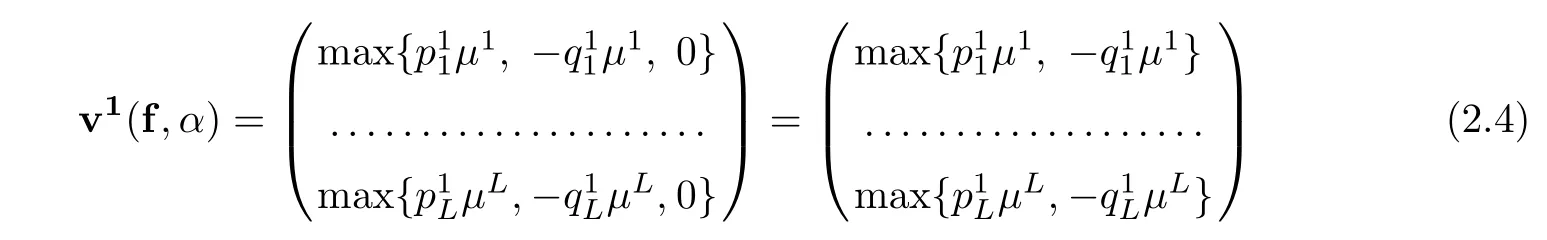
with µ1=y1TAz+y1Tf +αy1Ten,..., µL=yLTAz+yLTf +αyLTen.

Therefore,(1.3)can be converted to the following SOCP over(z,α,γ,f)∈

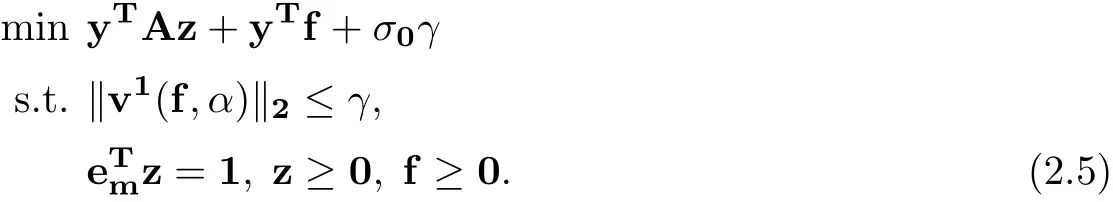
It is easy to show that (2.5) can be rewritten as (2.3) combining with (2.4), that is, the robust counterpart of (1.1) can be formulated as (2.3).

Similar to (2.2), if ZUis constructed as follows:

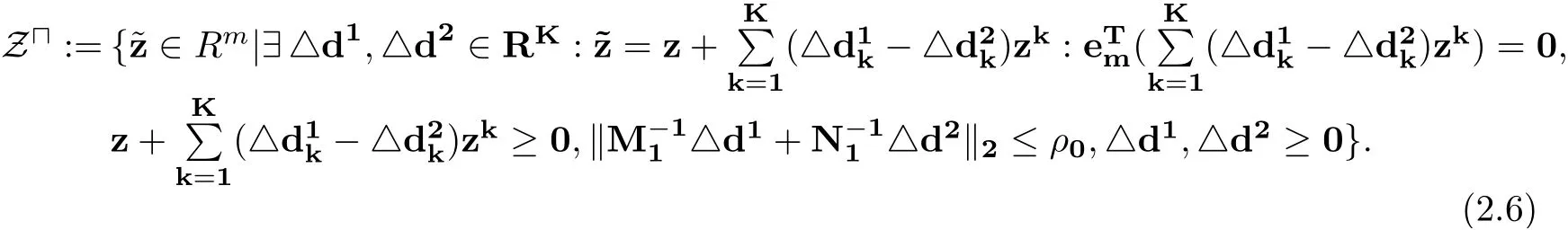
Then the robust counterpart of (1.2) can be formulated as an SOCP over varies∈

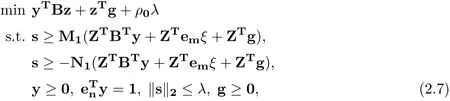
where Z =(z1z2··· zK)∈

In what follows, we focus on the KKT conditions for problems (2.3) and (2.7). It is easy to show that the KKT conditions for (2.3) can be written as

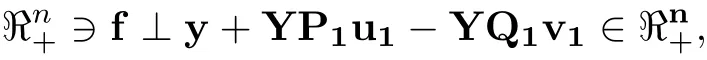
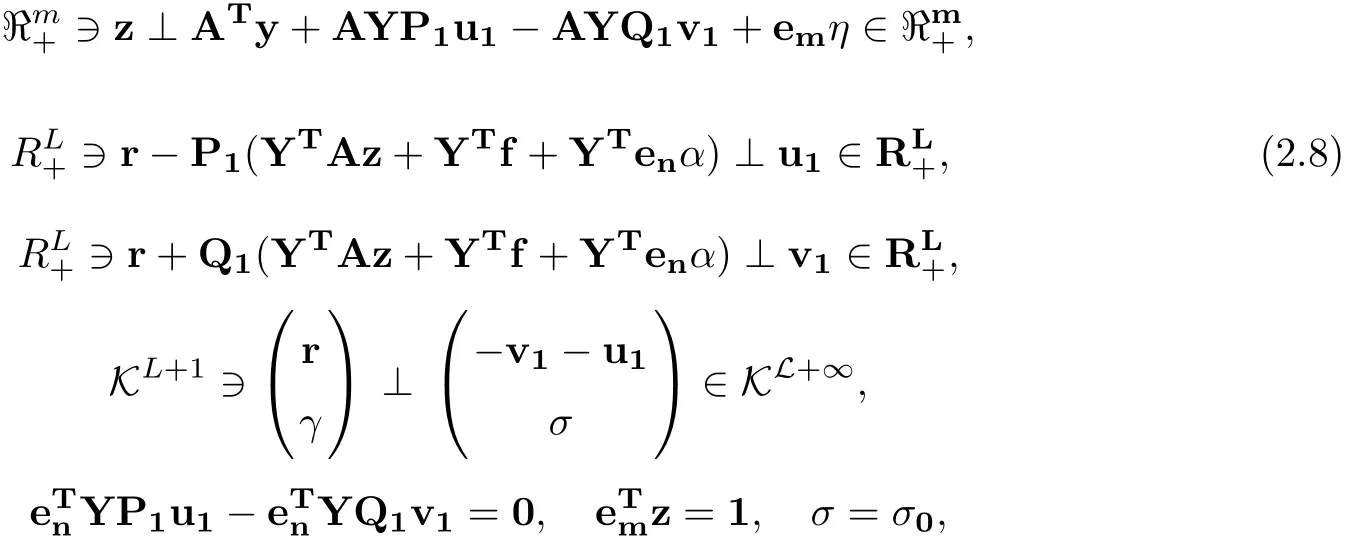
where u1,v1∈, η,σ ∈are the Lagrangian multipliers.

similarly, the KKT conditions for (2.7) can be expressed as

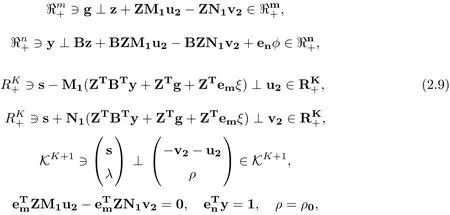
where u2,v2∈, φ,ρ ∈are the Lagrangian multipliers.

Consequently, the problem to find a pair of strategies (z,y) satisfying problems (2.3) and(2.7) simultaneously can be converted to the problem to find (z,y) satisfying the KKT conditions (2.8) and (2.9) simultaneously. The latter can be further formulated to an SOCCP (1.5)whereare two partitioned matrices as follows:

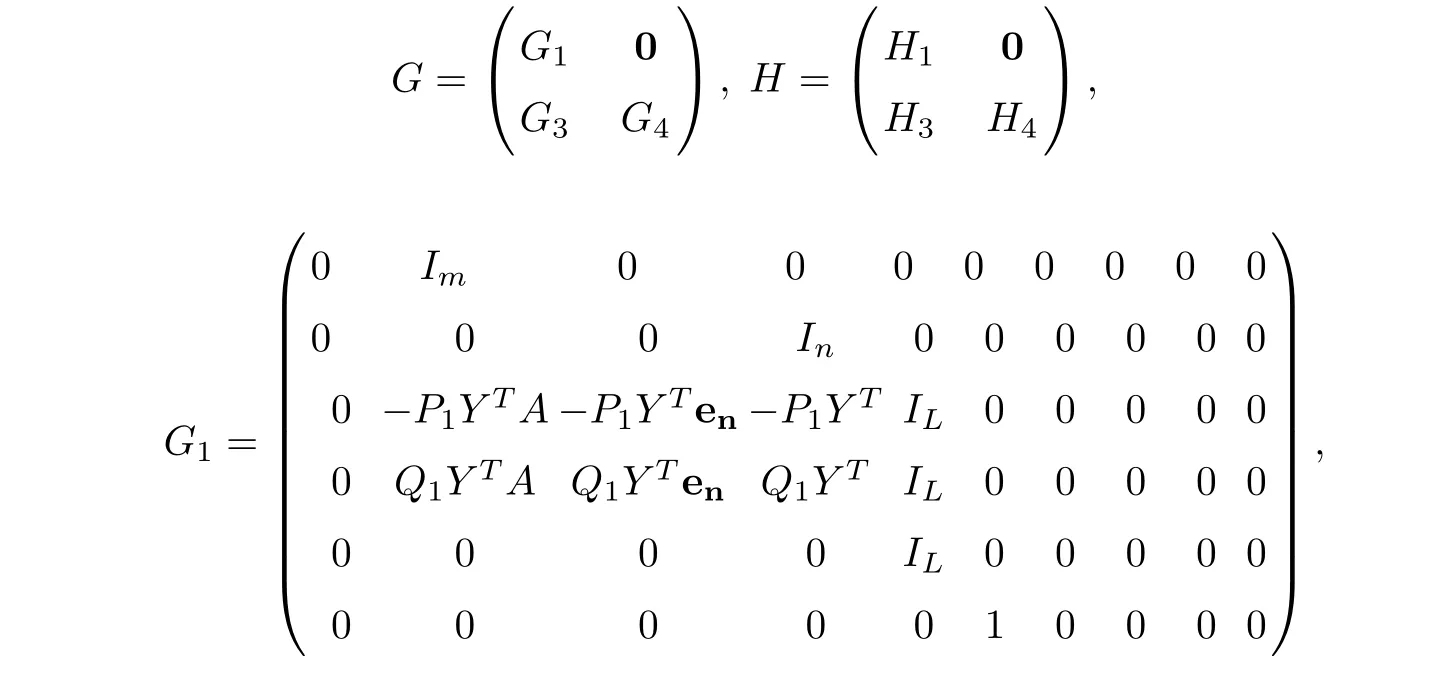
dT=(0 1 σ00 1 ρ0),qandrare two ς-dimensional zero vectors.

Therefore, for mixed strategy sets with asymmetric ellipsoidal uncertainty, we obtain the following result.

Theorem 2.2Let mixed strategy sets be given as (2.2) and (2.6) withnorm respectively, then solving the robust cooperative dual equilibrium for problems (1.1) and (1.2)can be formulated as an SOCCP as above.

§3. Numerical Experiments

In the previous sections, we have shown that the robust cooperative dual equilibrium problems for the bimatrix game with asymmetric strategy uncertainty can be formulated as an SOCCP. In this section, we present a numerical experiment for robust cooperative dual equilibrium. We only consider the case where each player’s own strategies are uncertain with L=K =3 and m=n=3. While doing numerical experiments, we adopt the algorithm in [?]to solve the SOCCP in Theorem 2.2. Consider the bimatrix game with cost matrices:

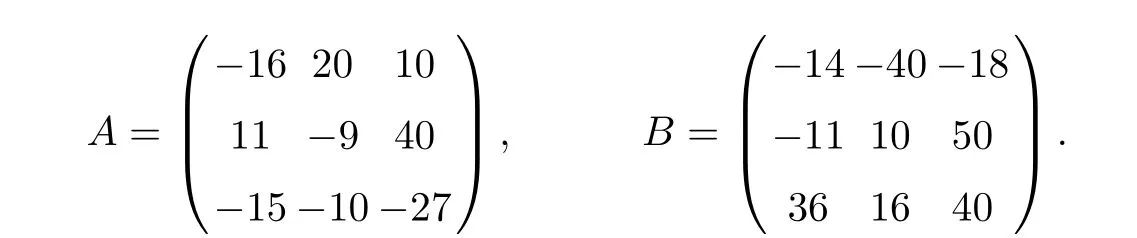
We select the matrices of perturbation directions as

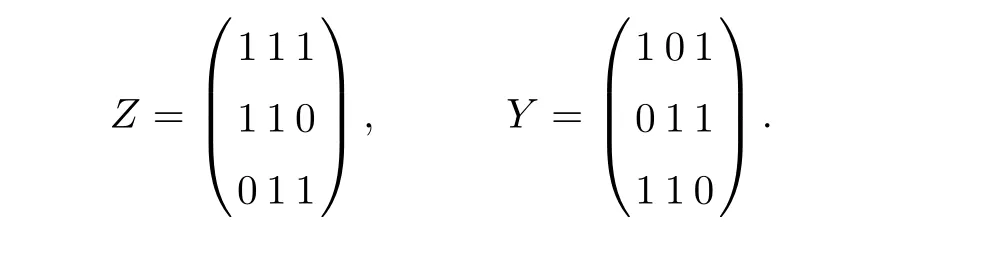
For simplicity, we select the matrices of deviation measures as P1= I3,Q1= 2I3,M1=0.5I3and N1= I3. Particularly, if the control parameters σ0and ρ0are equal to zeros, the corresponding model reduces to the primitive situation,that is,there is no perturbation in their strategies and the two player adopt pure strategies. In this situation, the strategies for player one and player two are=(0 1 0) and(1 0 0) and the corresponding cost values are 20 and −40 respectively. The robust cooperative dual equilibrium for various σ0and ρ0are listed in Table 1. The meaning of the columns in Table 1 is listed below:

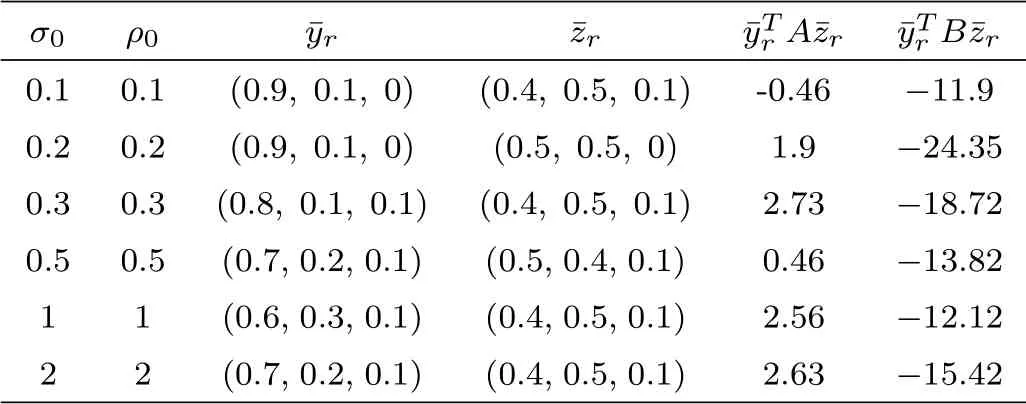
Table 1: Robust cooperative dual equilibrium with asymmetric uncertainty under l2−norm

From table 1, we see that (a) There is little change about the strategies for player one when control parameters vary from 0.1 to 2. This implies that the cooperative dual equilibrium model is almost robust for player one. (b) As the parameters increase continuously, the cost values are not always steady increase while alternately change which implies that the parameters σ0and ρ0and the direction matrices play important roles in controlling the robustness and optimality. (c)How to choose an appropriate parameter or direction matrix between robustness and optimality is an important while significantly hard work. (d) The work can be applied to the optimal reinsurance. For example,suppose that the two players one and two denote insurer and reinsurer respectively and suppose that they reach a premium agreement with respect to some types of insurance and the corresponding price. The insurer pays the premium to the reinsurer to transfer some risk. The reinsurer receives premium from the insurer to take the corresponding risk transferred from the insurer. Therefore, ¯yTrA¯zrdenotes the insurance premium with sign plus (omitted) which the insurer pays to the reinsurer and ¯yTrB¯zrdenotes the insurance premium with sign minus which the reinsurer obtains from the insurer. In this situation, we can choose the cost matrix A for insurer as above and let B = −A be the cost matrix for reinsurer.