On Products and Diagonals of Mappings in Generalized Topological Spaces

CAO Chun-fang, SHEN Rong-xin

(1. Department of Mathematics, Taizhou University, Taizhou 225300, Jiangsu, P.R. China; 2. Department of Mathematics, Taizhou University, Taizhou 225300, Jiangsu, P.R. China )

Abstract: Based on the theory of products of generalized topologies, we introduce the product mappings and the diagonal mappings in generalized topological spaces in this paper.We investigate some basic properties (especially, the continuity, openness and closedness) of the product mappings and the diagonal mappings in generalized topological spaces. Some applications are given to answer two questions raised in [3].

Key words: Product mappings; Diagonal mappings; Generalized topology

§1. Introduction

In recent years, the theory of generalized topological spaces founded by Cs´asz´ar has been extensively studied, which is one of the most important development of general topology, see[1-3, 10, 12-20, 23]. In [9], Cs´asz´ar introduced the Cartesian product of generalized topologies and built some fundamental results on this topic. The second author gave some remarks on product of generalized topologies to discuss the connectedness and compactness of products of generalized topologies in [22]. In this paper, we will discuss the properties of the product and the diagonal of the mappings in the realm of generalized topological spaces. As applications,we give answers to two questions raised in [3].

We recall some basic definitions and notions in generalized topological spaces. Let X be a nonempty set and ExpX be the power set of X. The subset µ of ExpX is called a generalized topology (briefly GT) on X if ∅∈µ and every union of some elements of µ belongs to µ. A set with a GT is said to be a generalized topological space (briefly GTS). The elements of µ are called µ-open sets (briefly, open sets) and their complements are called µ-closed sets (briefly,closed sets). The generalized interior of a subset A of X denoted by iµA is the union of allµ-open sets included in A, and the generalized closure of A denoted by cµA is the intersection of all µ-closed sets including A. It is easy to verify that cµA=X −iµ(X −A)and iµA=X −cµ(X −A)[7]. For a generalized topological space (X,µ), we denote Mµby the union of all elements of µ.We say the GT µ is strong if X ∈µ. Obviously, the GT µ is strong if and only if Mµ=X.

Let(X,µX)and(Y,µY)be two generalized topological spaces and f be a mapping X →Y.We say that f is (µX,µY)-continuous (briefly continuous) if U ∈µYimplies f−1(U) ∈µX, f is (µX,µY)-open (briefly open) if U ∈µXimplies f(U)∈µY, and f is (µX,µY)-closed (briefly closed) if X −F ∈µXimplies Y −f(F)∈µY. It is obvious that µXis strong whenever µYis strong and f : X →Y is continuous, and µYis strong whenever µXis strong and f : X →Y is open and surjective.

§2. The product of GT’s

Lemma 2.1[9]

Lemma 2.2[22]Let K0be a finite subset of K. If Ak∈{Mk,Xk} for each k ∈K K0,then iA=

Lemma 2.3[9]The projection pkis (µ,µk)-open for each k ∈K.

Lemma 2.4[9]If all µk’s are strong, then every pkis (µ,µk)-continuous.

Theorem 2.5The setis µ-closed inif and only if Akis µk-closed in

Xkfor each k ∈K.

ProofSuppose the setis µ-closed, thenAk. By lemma 2.1,it follows that ckAk=Ak. So Akis µk-closed set in Xkfor each k ∈K.

Conversely, if every Akis a µk-closed set in Xk, then ckAk=Akfor each k ∈K. Then

Theorem 2.6The setisµ-open inif and only if Akisµk-open in Xkfor each k ∈K and there exists a finite subset of K0such that Ak=Mkfor each k ∈KK0.

ProofSufficiency is obvious, to show the necessity. Suppose the setµ-open inBy Lemma 2.3, Akis open in Xkfor each k ∈K. Take arbitrary standard open set B contained in A with the formBk, where Bk= Mk(k ∈K K0) for some finite K0⊂K. Then Ak=Mkfor each k ∈KK0.

§3. The Products of The Mappings

Let K be a nonempty index set. Suppose we are given two families of generalized topological spaces {Xk}k∈Kand {Yk}k∈Kand a family of mappings {fk}k∈K, where fk: Xk→Yk.The mapping assigning to the pointt he point {fk(xk)}is called the cartesian product (briefly, the product) of the mappingsand is denoted by

Consider in the following M is denoted by the union of all elements of µX,is denoted by the union of all elements of µY, Mkis denoted by the union of all elements of µXk,is denoted by the union of all elements of µYk, pkis denoted by the projection X →Xkandis denoted by the projection Y →Yk.

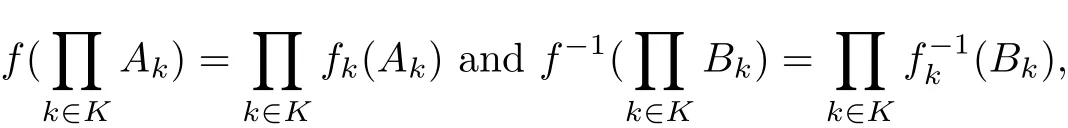
where fk: Xk→Yk, Ak⊂Xkand Bk⊂Yk.

Theorem 3.1Let K be a nonempty index set, {Xk: k ∈K} and {Yk: k ∈K} be two classes of generalized topological spaces,For a finite set K0⊂K, we have

(1)If all mappings fk: Xk→Yk(k ∈K) are continuous and spaces Yk(k ∈K K0) are strong, thenis continuous.

Proof(1) Let U be a standard open setin Y, where K1is a finite subset of K and Ukis an open set in Ykfor each k ∈KK1. Without loss of generality,we may assume that K0⊂K1. Then we have Since every fk: Xk→Ykis continuous, every f−1(Uk) is an open set in Xk(k ∈K1). So f−1(U) is an open set in X. Thus f is continuous.

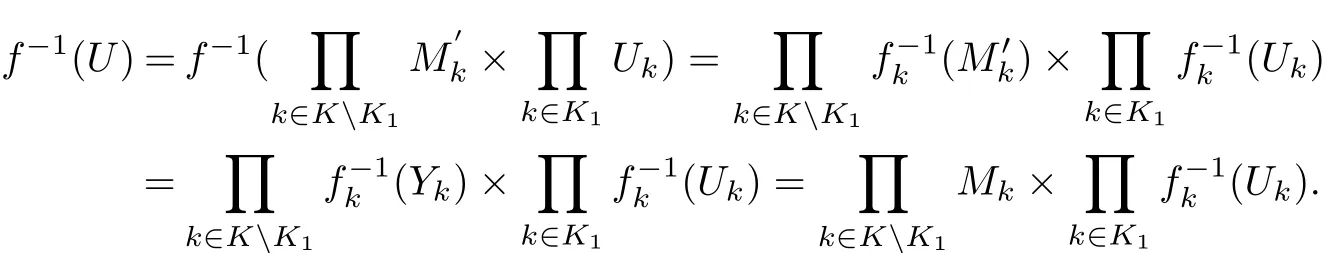
(2)Let k0∈K. For any open set Vk0in Yk0(k0∈K),the set×Vk0is open in Y.So the setis open in X by the continuity of f. Thenis an open set in Xk0by theorem 2.6. Thus fk0: Xk0→Yk0is continuous.

The following example shows that the condition that “all but finite many Yk’s are strong”can not be omitted in above.

Example 3.2Let K be a infinite index set, Xk= Yk= {a,b} for each k ∈K andµ1={∅,{a},{a,b}}, µ2={∅,{a}}. We consider a family of functions fk: (Xk,µ1)→(Yk,µ2)(k ∈K) defined by fk(a) = a,fk(b) = b. It is easy to see that every fkis continuous and f =X →Y is not continuous.

Theorem 3.3Let K be a nonempty index set, {Xk: k ∈K} and {Yk: k ∈K} be two classes of generalized topological spaces,Then the product mapping f =X →Y is open if and only if every fk: Xk→Ykis open for each k ∈K and there exists a finite subset K0⊂K such that fk(Mk)=∈KK0.

ProofSuppose that f is an open mapping. Thenis an open set in Y. It follows from theorem 2.6 thatall but finitely many members of K. Now let k0∈K andbe an open set inThen the setis open in X. Since f is open,is open in Y. Then we have that fk0(Uk0) is an open set in Yk0. So fk0is open.

Corollary 3.4Let K be a nonempty index set, {Xk: k ∈K} and {Yk: k ∈K} be two classes of generalized topological spaces. If Xkis strong and fk: Xk→Ykis open and surjective for each k ∈K, then the product mappingis open.

Theorem 3.5Let K be a nonempty index set, {Xk: k ∈K} and {Yk: k ∈K} be two classes of generalized topological spaces,for each k ∈K. Ifis closed, then fkis closed for each k ∈K.

ProofLet k0∈K and Fk0be a closed set in Xk0. Then the setis close d in X by theroem 2.5. Sois closed in Y. Thus the set fk0(Fk0) is a closed set in Yk0. So fk0is closed.

Remark 3.6The converse of the theorem 3.5 is not valid in general, even when K is finite and {Xk: k ∈K} and {Yk: k ∈K} are classes of topological spaces, see [11, Example 2.3.28].

§4. The Diagonals of The Mappings

Suppose we are given a generalized topological space X, a family {Yk}k∈Kof generalized topological spaces and a family of mappings {fk}k∈K, where fk: X →Yk. The mapping f:X →Y =assigning to the point x ∈X the point {fk(x)}Ykis called the diagonal of the mappings {fk}k∈Kand is denoted by ∆k∈Kfk.

For the diagonal f =∆k∈Kfk, we have

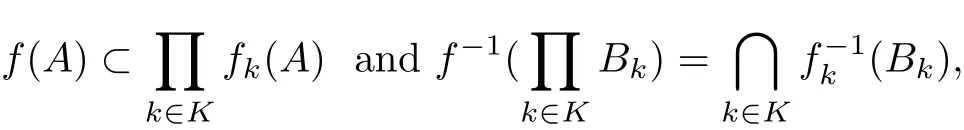
where fk: X →Yk, A ⊂X and Bk⊂Yk.

Theorem 4.1If every Ykis strong and f = ∆k∈Kfk: X →Y is continuous, then every fk: X →Ykis continuous.

ProofFor every open set Vkin Yk,the setis open in Y,since every Ykis strong.Sois an open set in X. Thus every fk: X →Ykis continuous.

The following example 4.2 shows that the strongness of the images can not be omitted in theorem 4.1, and example 4.3 shows that the converse of theorem 4.1 is not valid.

Example 4.2Let X = Y = {a,b,c} and µ1= {∅,{a}}, µ2= {∅,{c}}. We consider a mapping f1= id|X: (X,µ1) →(X,µ1) defined by f1(a) = a,f1(b) = b,f1(c) = c, and another mapping f2: (X,µ1) →(Y,µ2) defined by f2(a) = b,f2(b) = c,f2(c) = a. It is easy to verify that the mapping f =f1∆f2is continuous, and f2is not continuous.

Example 4.3Let X =Y ={a,b,c} and µ1=µ2={∅,{a,b},{a,c},{b,c},{a,b,c}}. We consider a mapping f1=id|X: (X,µ1)→(X,µ1)defined by f1(a)=a,f1(b)=b,f1(c)=c,and another mapping f2: (X,µ1)→(Y,µ2)defined by f2(a)=c,f2(b)=a,f2(c)=b. Obviously we have that both f1and f2are continuous. Since(f1∆f2)−1({a,b}×{a,b})={a,b}∩{b,c}={b}is not open in X, the mapping f =f1∆f2is not continuous.

The above examples also give answers to the questions raised in[3]. we recall some notations and definitions.

Definition 4.4[7]Let (X,µ) be a generalized topological space and A ⊂X. Then A is said to be

(1) α-open if A ⊂iµ(cµ(iµ(A)));

(2) σ-open if A ⊂cµ(iµ(A));

(3) π-open if A ⊂iµ(cµ(A));

(4) β-open if A ⊂cµ(iµ(cµ(A))).

Definition 4.5[3]Let (X,µ) andbe GTS’s . Then a mapping f : X →is said to be

Remark 4.6The following implications can be verified easily.

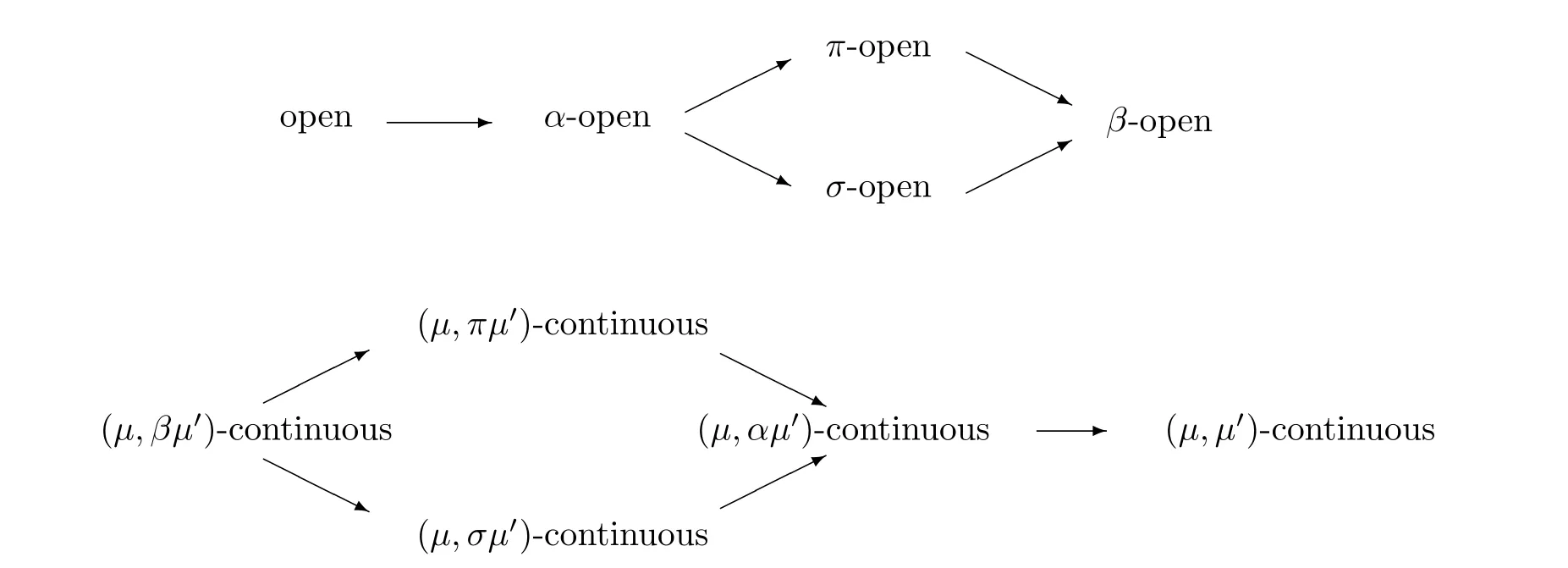
Question 4.7[3,Question1]Let (X,µ), () be two generalized topological spaces,f : X →be a mapping, and h be the graph mapping of f. Is f (µ,α)-continuous((µ,)-continuous) whenever h is (µ,-continuous ((µ,)-continuous)?

Question 4.8[3,Question2]Let (X,µ), () be two generalized topological spaces,f : X →be a mapping, and h be the graph mapping of f. Is h (µ,)-continuous (resp,.(µ,βcontinuous,(µ,)-continuous,(µ,)-continuous)whenever f is(µ,α-continuous(resp., (continuous, (µ,σ-continuous, (µ,)-continuous)?

The answer to above questionsLetbe the space Y, and f be the mapping f2in the example 4.2, then the graph mapping h of f equals to the diagonal f1∆f2. Note that the set {a}×{c} is the unique nonempty open set in. Then it is easy to verify that{a}×{c}is also the unique nonempty π-open(α-open)set inIt follows that the graph mapping h = f1∆f2is (µ,α-continuous ((µ,-continuous). We have already proved in example 4.2 that f2is not continuous, which gives a negative answer to question 4.7. Further we letthe space Y,and f be the mapping f2in the example 4.3,then the graph mapping h of f equals to the diagonal f1∆f2. It is easy to check that the class of all β-open sets inis {∅,{a,b},{a,c},{b,c},{a,b,c}}. So the mapping f2is (µ)-continuous. We have already proved in example 4.3 that f1∆f2is not continuous, which gives a negative answer to question 4.8.

Theorem 4.9If the diagonal f = ∆k∈Kfk: X →Y is open, then every mapping fk:X →Ykis open.

ProofThe conclusion follows from the equality fk=◦f and lemma 2.3, which states that the projectionY →YKis always open.

Remark 4.10The converse of the theorem 4.9 is not valid in general, even when {Yk:k ∈K} is a finite class of topological spaces, see [11, Example 2.3.33].

In order to discuss the closedness of diagonal of mappings,we recall the axioms of separation for the generalized topological spaces, which were discussed in [10, 12-13, 15-16, 19-20].

Definition 4.11[12,19]Let X be a generalized topological space. X is called T1if for every pair of distinct points x1,x2∈X there exists an open set U ⊂X such that x1∈U and x2. X is called T3if X is T1and for every point x ∈X and every closed set F ⊂X such that xthere exist two open sets U1, U2⊂X such that x ∈U1, F ⊂U2and U1∩U2=∅.

Theorem 4.12If a generalized topological space X is a T3-space, then for every x ∈X and every open neighborhood V of x, there exists an open neighborhood U of x such that

cU ⊂V.

ProofSuppose that X is a T3-space. By the definition,there exist two open sets U1, U2⊂X such that x ∈U1, X V ⊂U2and U1∩U2= ∅. Then we have U1⊂X U2⊂V, which implies that cU1⊂V.

Theorem 4.13A mapping f: X →Y is closed if and only if for every set B ⊂Y and every open set U ⊂X which contains f−1(B), there exists an open set V ⊂Y containing B such that f−1(V)⊂U.

ProofSuppose that f: X →Y is closed, B is a subset of Y and U is an open subset of X which contains f−1(B). So the set V =Y f(XU)is open in Y and contains B. Moreover,

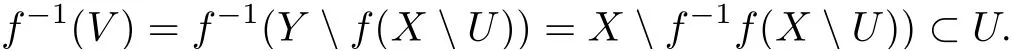
Conversely, let us take a closed set F ⊂X. It suffices to show f(F) is closed in Y. Note that the set U =X F is open in X, and for B =Y f(F) we have

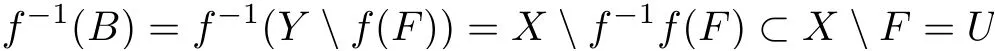
By the condition in the theorem, there exists an open subset V of Y such that Y f(F) ⊂V and f−1(V)⊂U, i.e., f−1(V)∩F =∅. The last equality implies that V ∩f(F)=∅, i.e., that V ⊂Y f(F). So we have that V =Y f(F) and thus f(F) is closed in Y.

Theorem 4.14Let X be a GTS, Y1a T1-GTS, Y2a T3-GTS and fibe the mapping X →Yifor i=1,2. If both f1and f2are closed and continuous, then the diagonal f =f1∆f2is closed.

ProofSuppose a closed set A ⊂X and a point (y1,y2) ∈(Y1×Y2)f(A). We haveand thusNote thatis a closed set in X, since Y1is T1and f1is continuous. Then X (A ∩) is an open set in X.By theorem 4.12 and theorem 4.13, there exists an open neighborhood V2⊂Y2of y2satisfying)⊂X(A ∩)). Then we have⊂X(A ∩). By theorem 4.13,there exists an open neighborhood V1⊂Y1of y1satisfying⊂X(A ∩cV2)), thus A ∩(V2)=∅. The equality shows that f−1(V1×V2) ⊂X A, So V1×V2is an open neighborhood of (y1,y2) in Y1×Y2satisfying that V1×V2∩f(A)=∅, which implies that f(A) is closed in Y1×Y2. Therefore, the diagonal f is closed.

Remark 4.15The closedness and continuity of the diagonal f1∆f2do not imply that f1and f2are closed even in topological spaces, see [11, Example 2.3.31].

It was shown in page 85 of[11]that theorem 4.14 can not be generalized to infinite diagonals.However, we still do not know that whether is it valid for finite index set with size bigger than two.

Question 4.16Let X be a GTS, Y1a T1-GTS and Y2,Y3··· ,Ynbe T3-GTS’s. If every mapping fi: X →Yiis closed and continuous for i = 1,2··· ,n, is then the diagonal f =f1∆f2···∆fnclosed?